汽車車輪胎唇-胎圈座間接觸壓力分布模型的構建*

單穎春，劉旺浩，劉獻棟，王杰功

(1.北京航空航天大學交通科學與工程學院，北京 100191; 2.新能源汽車高效動力傳動與系統控制北京市重點實驗室，北京 100191； 3.山東興民鋼圈股份有限公司，龍口 265716)

2016078

汽車車輪胎唇-胎圈座間接觸壓力分布模型的構建*

單穎春1，2，劉旺浩1，2，劉獻棟1，2，王杰功3

(1.北京航空航天大學交通科學與工程學院，北京 100191; 2.新能源汽車高效動力傳動與系統控制北京市重點實驗室，北京 100191； 3.山東興民鋼圈股份有限公司，龍口 265716)

采用J.Stearns提出胎唇-胎圈座之間的接觸壓力按余弦規律分布的假定進行車輪在徑向載荷作用下的強度仿真所得到的輪輞等效應力與實驗測試結果有明顯較大偏差。為解決此問題，本文首先對胎唇-胎圈座間接觸壓力分布進行了實際測試，獲得施加徑向載荷引起的分布壓力的變化曲線；接著，基于該壓力分布曲線擬合出新的胎唇-胎圈座間接觸壓力分布模型；最后基于該新模型進行仿真。結果表明：采用所構建胎唇-胎圈座接觸壓力分布模型，可獲得比較符合實際的輪輞等效應力分布。

鋼制車輪；胎唇；胎圈座；接觸壓力分布；仿真

前言

按照國家標準GB/T 5909—2009和GB/T 5334—2005，汽車鋼制車輪須滿足彎曲疲勞試驗和徑向疲勞的臺架試驗要求，歐美以及日本均有類似標準。為縮短鋼制車輪研發周期、減少試驗成本，在設計階段通過有限元方法進行車輪的彎曲疲勞試驗和徑向疲勞試驗仿真已成為企業進行產品開發的手段。

目前，國內外[1-8]研究人員對車輪在徑向載荷作用下的應力仿真中，多采用J.Stearns提出的在輪輞胎圈座上以一定角度范圍按余弦函數分布的壓力進行加載[9]。但本文中通過對車輪在徑向載荷作用下的應力測試發現，按照J.Stearns提出的方法進行加載獲得的一定區域的最大應力仿真結果總是比實測相應區域的最大應力大60%甚至90%。這導致根據應力仿真結果進行的車輪壽命估算結果明顯低于車輪的實際壽命，使得難以進行有效的車輪輕量化設計。若在仿真模型中構建輪胎[10-11]結構，針對車輪輪胎總成進行徑向載荷作用下的強度仿真[12]，可以避免引入胎圈座與胎唇之間的載荷分布函數，但輪胎本身屬于超彈性不可壓縮復合材料，并且輪胎與輪輞間存在接觸面，仿真時間長且過程中極易出現計算不收斂的情況。此外，在車輪的徑向疲勞仿真分析中，并不十分關心輪胎承受載荷及強度問題，更關心的是它傳遞到輪輞的真實載荷，因此在車輪徑向仿真模型中可不必考慮輪胎模型。

針對以上問題，本文中首先對徑向載荷作用下胎唇-胎圈座間接觸壓力分布進行了實驗測試，并在測試數據的基礎上構建了接觸壓力數學模型；接著，對車輪在徑向載荷作用下的應力分布進行了仿真，并將仿真結果與實驗測試結果進行比較和分析。結果表明，仿真計算的應力結果與實測的應力結果吻合較好。這可為鋼制車輪在徑向載荷作用下的疲勞壽命分析提供更準確的應力計算結果，為車輪的輕量化設計奠定基礎。盡管本文中的研究是針對鋼制車輪進行的，但所構建的接觸壓力數學模型對于鋁制車輪以及其他材料車輪的仿真也具有重要意義。

1 問題的提出

首先采用目前國內外在處理車輪徑向載荷時的常用方法，即J.Stearns提出的在輪輞胎圈座上以一定角度范圍按余弦函數分布的壓力進行加載，得到應力仿真結果；然后進行徑向載荷下的輪輞應力測試，得到輪輞內側一定角度范圍內的應力數據；最后將仿真數據與實測數據進行對比分析。分析發現，按照J.Stearns提出的方法進行加載獲得的一定區域的最大應力仿真結果總是比實測相應區域的最大應力大60%甚至90%。因此，為得到準確的應力結果，在仿真分析中不宜直接采用基于J.Stearns的胎圈座上載荷分布模型，須尋求一種更能準確描述胎圈座上壓力分布規律的模型。

1.1 基于J.Stearns的載荷分布模型的仿真分析

根據文獻[9]，徑向加載的示意圖如圖1所示。

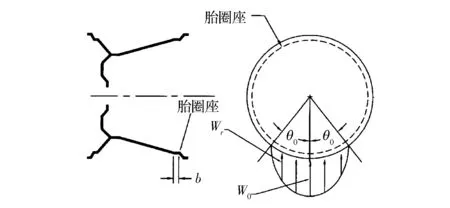
圖1 輪胎徑向載荷分布示意圖

圖1中：Wr為車輪徑向分布力 ；W0為最大徑向分布力；b為胎圈座受力寬度；θ0為徑向載荷作用的最大偏轉角。

根據J.Stearns的理論，車輪徑向分布力與最大徑向分布力間的關系為

(1)

對式(1)進行積分得

(2)

(3)

(4)

式中:W為徑向集中力；rb為輪胎座半徑 。

文獻[9]中指出，徑向載荷加載的最大偏轉角約為40°，故本文中在進行仿真分析時，分別計算了徑向載荷最大偏轉角θ0分別為36°，40°和45°時的情況。由于在輪輞胎圈座的分布力作用在輪輞上的近端和遠端兩側，所以式(4)中徑向集中力W為實驗載荷的一半，而實驗載荷為71kN，所以W=35.5kN。另外，胎圈座受力寬度b=35mm，胎圈座半徑rb=283mm。

當θ0=36°時，W0=4.48MPa，有

Wr=4.48cos(2.5θ)

(5)

當θ0=40°時，W0=4.03MPa，有

Wr=4.03cos(2.25θ)

(6)

當θ0=45°時，W0=3.58MPa， 有

Wr=3.58cos(2θ)

(7)

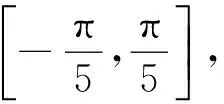
圖2 J.Stearns仿真加載模型

采用10節點四面體單元中的C3D10I對車輪結構進行離散，得到的仿真結果如圖3所示。

圖3 按J.Stearns所述方法加載的仿真結果

1.2 徑向載荷作用下輪輞應力測試

對徑向載荷作用下輪輞應力進行實驗測試，整個測試過程中將車輪安裝在車輪徑向疲勞試驗機的試驗臺上，如圖4所示。采用美國HBM公司的eDAQ型應變儀進行輪輞應力的測試及數據處理，測點布置在輪輞內側，如圖5所示。實驗中裝配的是全鋼絲子午線重載輪胎雙錢RR100(11R22.5)。

圖4 實驗設備圖

圖5 車輪徑向實驗測點

車輪上安裝輪胎后充氣使其達到額定胎壓，將裝胎后的車輪安裝在車輪徑向疲勞試驗機的試驗臺上，將測點的中間位置對準轉鼓，使車輪靜止不動且在轉鼓上不施加周向轉矩。將應變儀的數據進行清零，即輪輞應力測試結果中不包含輪胎壓力在輪輞中產生的應力。通過控制臺向車輪施加徑向載荷，在施加載荷的過程中，連續采集數據至載荷加到71kN，處理后的實驗結果如表1所示。各測點位置如圖6所示。

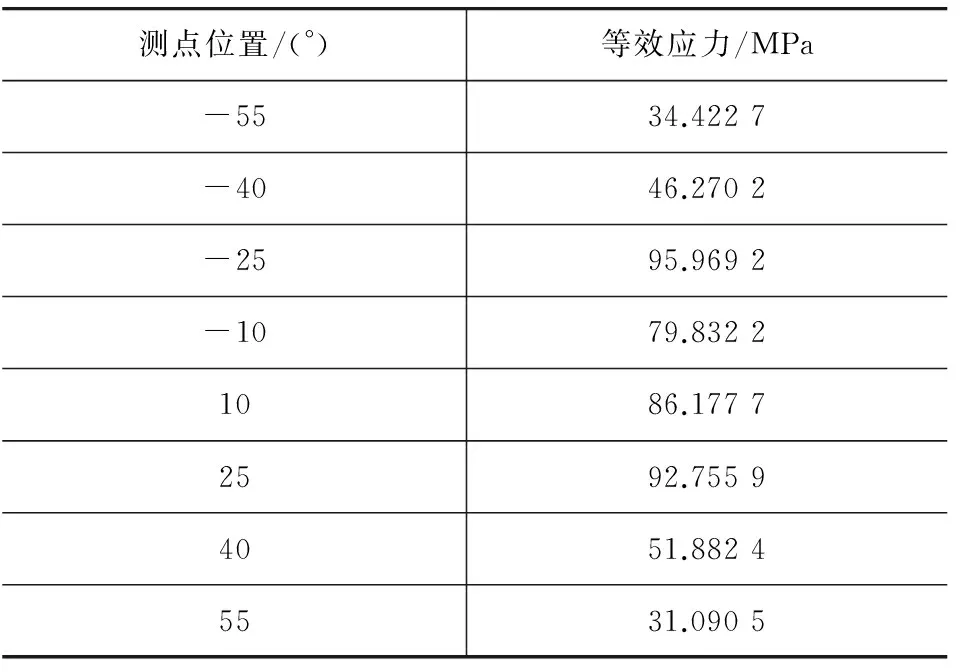
表1 各測點應力數據

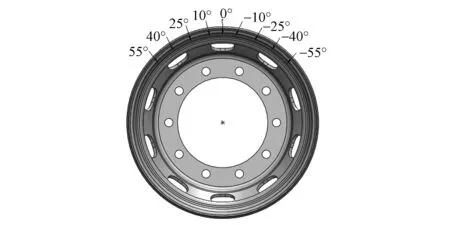
圖6 應力測點位置圖

1.3 基于J.Stearns的載荷分布模型的仿真結果與實測結果的對比分析

不同最大載荷偏轉角下的仿真結果在此分別用J-36°、J-40°和J-45°來表示。針對J-36°的仿真結果，查詢輪輞內側每隔10°的等效應力值，共36個位置的應力數據，同理針對J-40°和J-45°的仿真結果也各查得36個位置的應力數據，將所得到的各個位置的應力數據及表1中的實測應力數據繪于同一圖中，得到基于J.Stearns的載荷模型的仿真結果與實測結果的對比圖，如圖7所示。

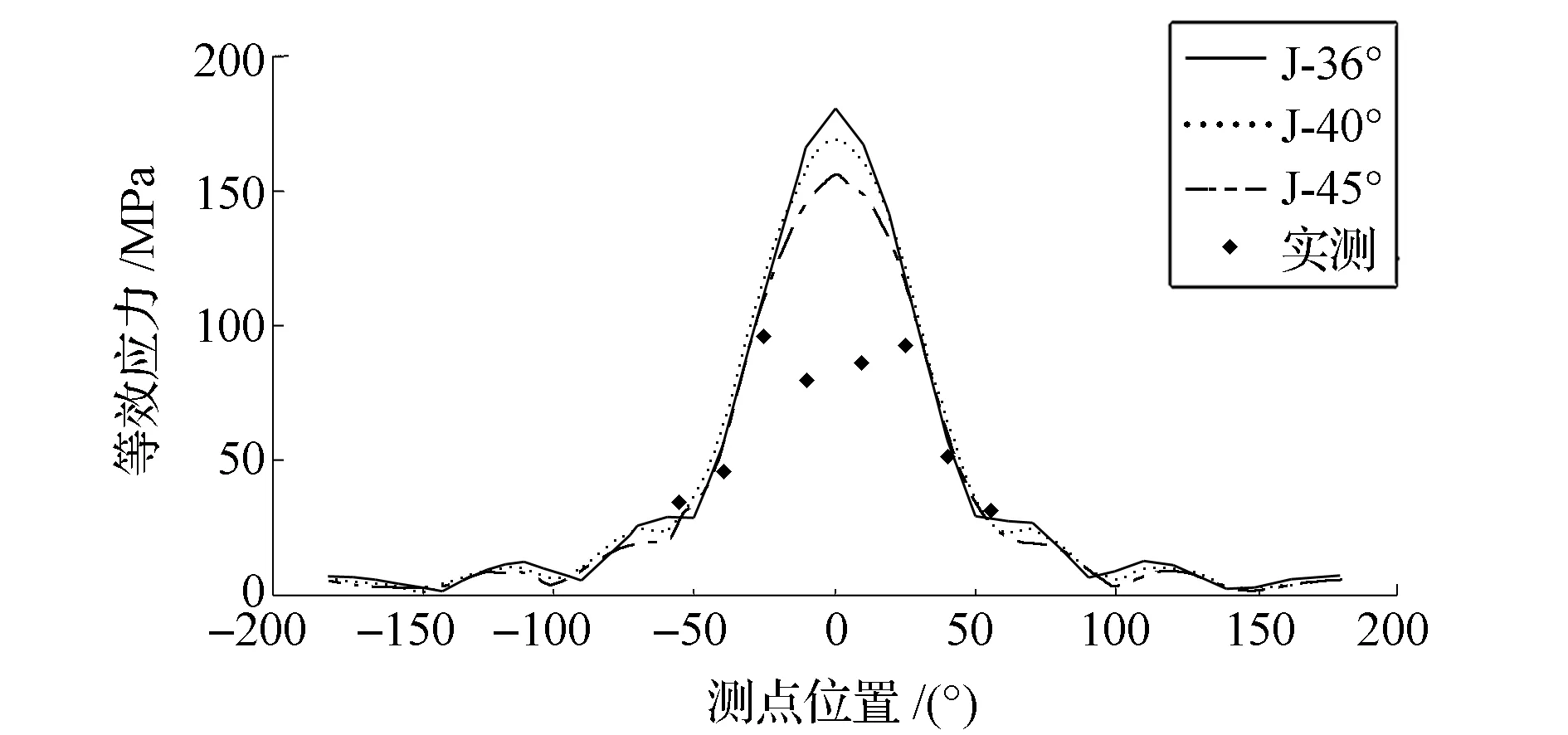
圖7 基于J.Stearns的載荷模型的仿真結果與實測結果的對比

由圖7可以看出，在低應力區域,三者都與實測應力吻合較好,但是,在高應力區域的偏差均較大。按J-36°加載的仿真結果在高應力區域比實測應力大90%左右,按J-40°加載的仿真結果在高應力區域比實測應力大79%左右,按J-45°加載的仿真結果在高應力區域比實測應力大63%左右。因此，隨著加載最大偏轉角的增加，輪輞高應力區域的仿真誤差在減小，但總體來說仿真結果的誤差均較大。為提高仿真計算的精度,必須對徑向載荷的加載函數形式進行改進。

2 胎唇-胎圈座間載荷模型構建

為得到可靠的胎唇-胎圈座間載荷模型，本文中進行了胎唇和胎圈座間接觸壓力的試驗測試，并基于測試數據進行載荷模型構建。本文中采用美國Tekscan公司生產的I-Scan測試儀器測量輪胎胎唇與輪輞間載荷分布，如圖8所示。將車輪裝配輪胎并充氣至額定胎壓0.8MPa后，安裝于車輪徑向疲勞試驗機上，試驗中通過轉動車輪來依次獲取車輪在整圈每間隔10°的壓強。傳感器連結器直接和計算機連接，并通過I-Scan軟件即時顯示傳感器的坐標及胎唇與胎圈座間壓強。

圖8 壓力分布分析設備測試圖

2.1 胎唇-胎圈座間載荷測試

首先測量轉鼓不施加徑向載荷時，僅由輪胎空氣壓力載荷和輪胎裝配的過盈應力引起的胎唇與胎圈座間壓強，然后測量轉鼓施加71kN徑向載荷時，由空氣壓力載荷、輪胎裝配的過盈應力和轉鼓施加的徑向載荷共同引起的胎唇與胎圈座間壓強。對各角度位置沿輪緣到深槽方向的壓強分布進行平均，可得到胎唇與胎圈座之間周向壓強平均分布圖，如圖9所示。接著通過換算(實際上即兩者相減)可方便得到僅由徑向載荷引起的胎唇與胎圈座之間周向壓強平均分布圖，如圖10所示。由圖10可以看出，輪輞近端(輪輞上靠近輪輻安裝位置的一端)和遠端的胎圈座在關于加載方向對稱的±50°左右的夾角范圍內為正壓強，而在此范圍外為負壓強。必須指出的是，胎唇與胎圈座之間的接觸壓強不可能為負值。此處的所謂正、負壓強，實際上是表示對車輪施加徑向載荷而引起的胎唇與胎圈座之間壓強的增量，即施加徑向載荷后，壓強為正的部位壓強增加，壓強為負的部位壓強減小。

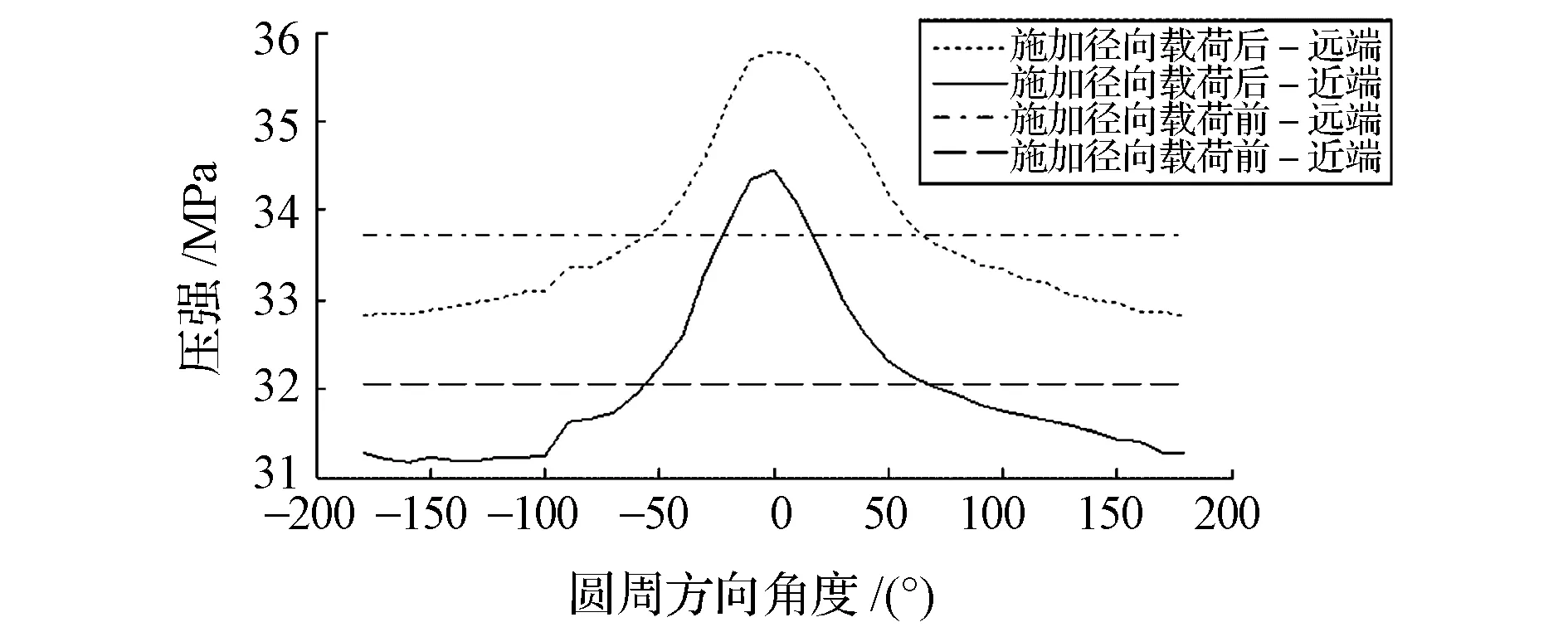
圖9 胎唇與胎圈座之間周向壓強的平均分布圖

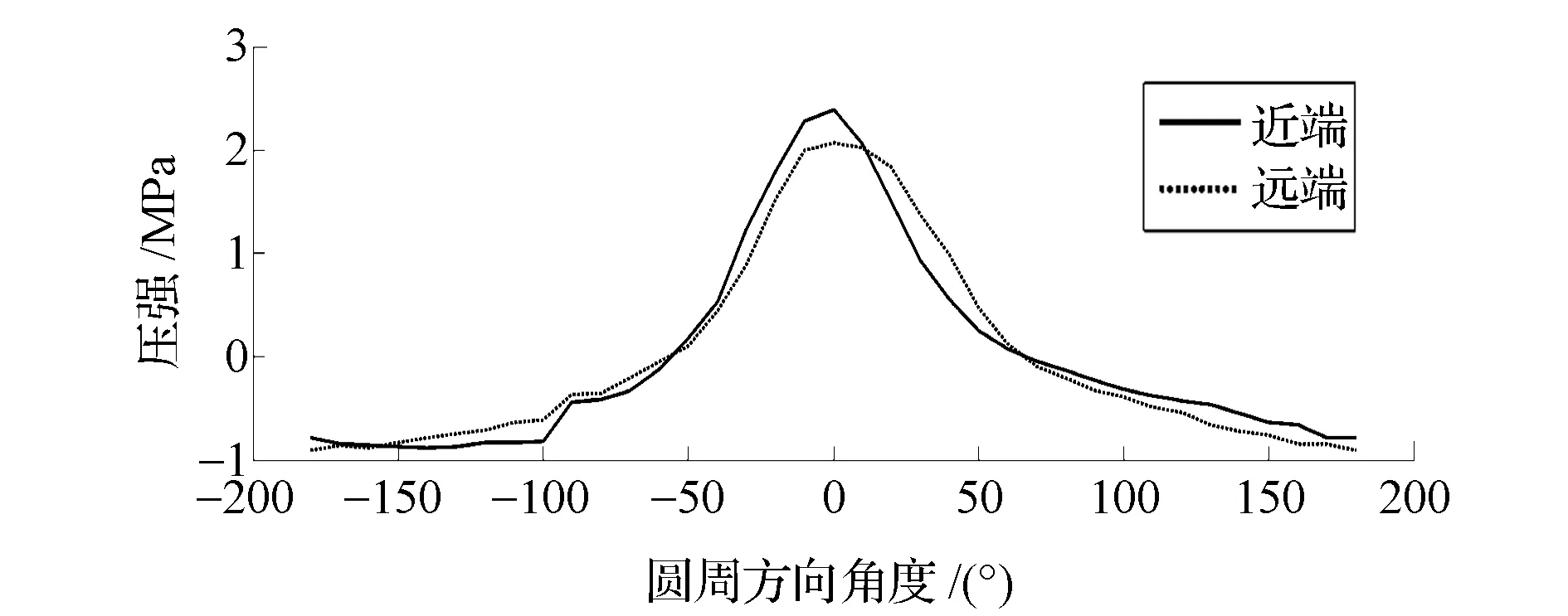
圖10 由徑向載荷引起的胎唇與胎圈座之間周向壓強平均分布圖

同時可以看出，J.Stearns提出余弦波狀的壓強僅分布在關于加載方向對稱的±40°范圍左右，在此范圍之外的壓強影響可以忽略。然而由上面的分析可知，在其它角度范圍為負壓強，并不能忽略。因此，這就是采用J.Stearns提出的方法進行加載仿真出現較大偏差的原因。

將胎唇、胎圈座間圓周方向壓強在胎圈座與胎唇的接觸面積上進行積分，可得到輪輞近端、遠端的徑向載荷，并可利用它們的和與實際加載數據的比較驗證本文中對載荷處理方法的正確性。積分后得到：

輪輞近端徑向載荷F近=34.427kN

輪輞遠端徑向載荷F遠=35.153kN

車輪徑向載荷F=F近+F遠=69.58kN

實驗中在車輪上施加的實際徑向載荷為71kN，由上述胎唇、胎圈座間載荷分布計算的車輪徑向載荷為69.58kN，與實際的集中載荷誤差為2%，因此，可證明上述處理胎唇、胎圈座載荷分布方法是可行的。

2.2 胎唇-胎圈座間載荷分分布模型構建

為了解決J.Stearns載荷模型中沒有考慮負壓強的問題，本文中基于整個胎圈座的壓強分布圖來構建新的載荷模型。即根據圖10的數據每隔10°取一點，則近端和遠端分別有36個點，繪出胎唇-胎圈座接觸壓力數據圖，如圖11所示。

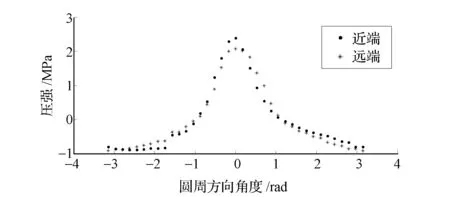
圖11 胎唇與胎圈座之間接觸壓力分布數據圖

由圖11可見，在一周即360°范圍上，輪輞遠端與近端載荷分布十分相似，并且均類似于墨西哥草帽，同時其中部曲線形狀似正弦曲線的一部分，因此，根據曲線擬合經驗，將曲線的函數假設為

(8)

式中:x為沿周向的角度，rad，取值范圍為[-π,π]；ai,bi和ci分別為擬合常數；i為擬合項數，本文中取4項；f(x)為胎唇、胎圈座間載荷，MPa。

針對某鋼制車輪在徑向載荷作用下的壓力分布測試結果，采用最小二乘法進行曲線擬合，得到擬合函數。擬合函數中的各個參數如下。

(1)輪輞近端胎唇-胎圈座接觸壓力分布函數中的各個參數為

(2)輪輞遠端胎唇-胎圈座接觸壓力分布函數中的各個參數為

利用這些參數獲得的擬合曲線如圖12所示。由圖可見，采用4個正弦函數進行擬合，具有足夠的擬合精度。

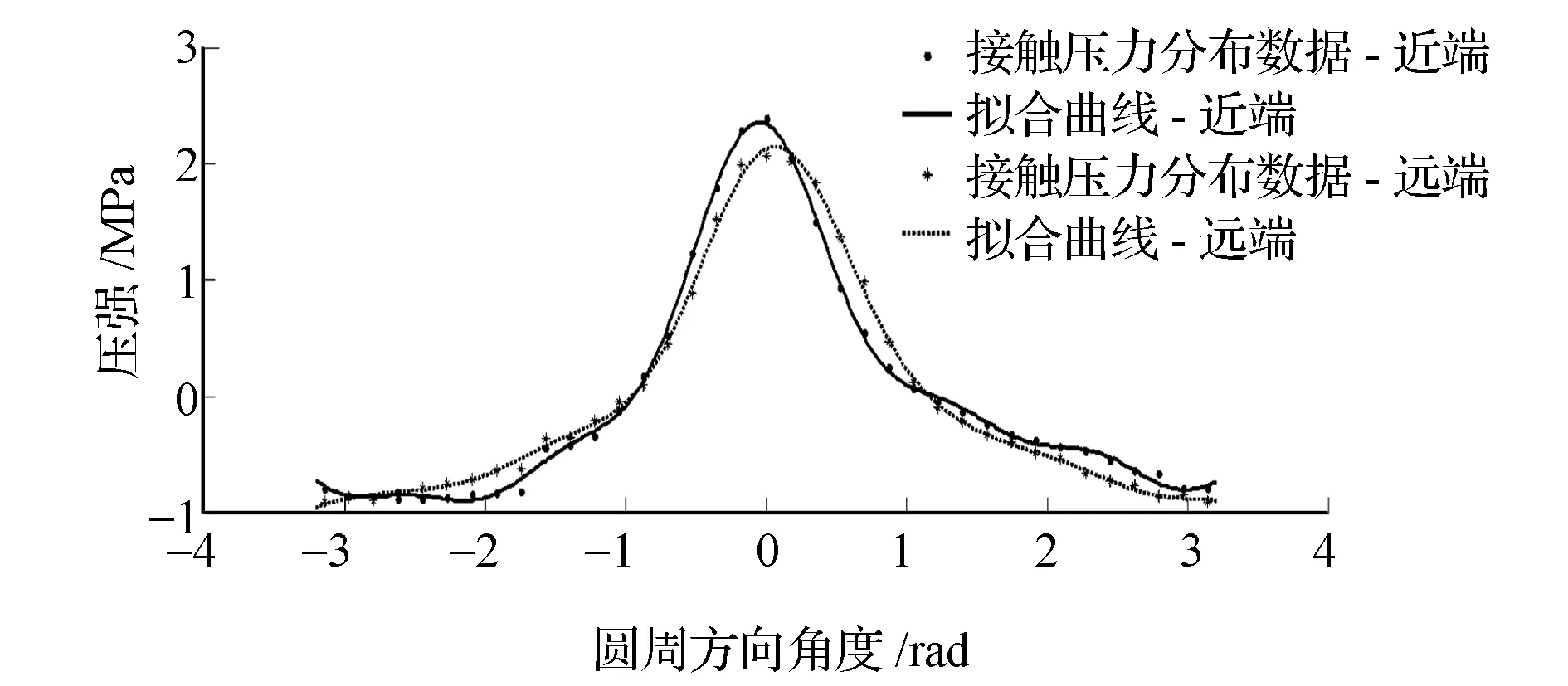
圖12 胎唇-胎圈座接觸壓力分布擬合圖

無論是鋼制車輪還是鋁制車輪，也不論車輪的大小，在與輪胎裝配后車輪本身的變形遠小于輪胎的變形，并且胎唇與胎圈座之間的載荷傳遞也無不同之處。另外，根據車輪的徑向加載實驗，隨著徑向載荷的增加，在輪輞內側的應力也基本呈線性增加。因此本文中構建的胎唇-胎圈座間載荷模型也可適用于其他大小以及材質的車輪。并且，所施加載荷如果不同，只須調整式(8)中的擬合常數ai，而其他參數不變。具體調整方法如下：假如在測試中采用的徑向集中載荷是88kN，則得到調整系數α=88/71=1.24。于是，近端參數變為

而遠端參數為

3 胎唇-胎圈座間載荷分布模型的驗證

將本文中所構建的載荷模型加載于車輪整圈胎圈座上，利用ABAQUS軟件進行仿真分析，得到車輪的應力分布，如圖13所示。考慮到實驗測試是對輪輞遠端進行的，對仿真結果的輪輞內側每隔10°的等效應力值進行查詢，得到36個測點的應力數據。將這36個測點的應力數據、實測結果以及按J.Stearns所述方法加載的仿真結果繪于同一圖中，得到圖14。

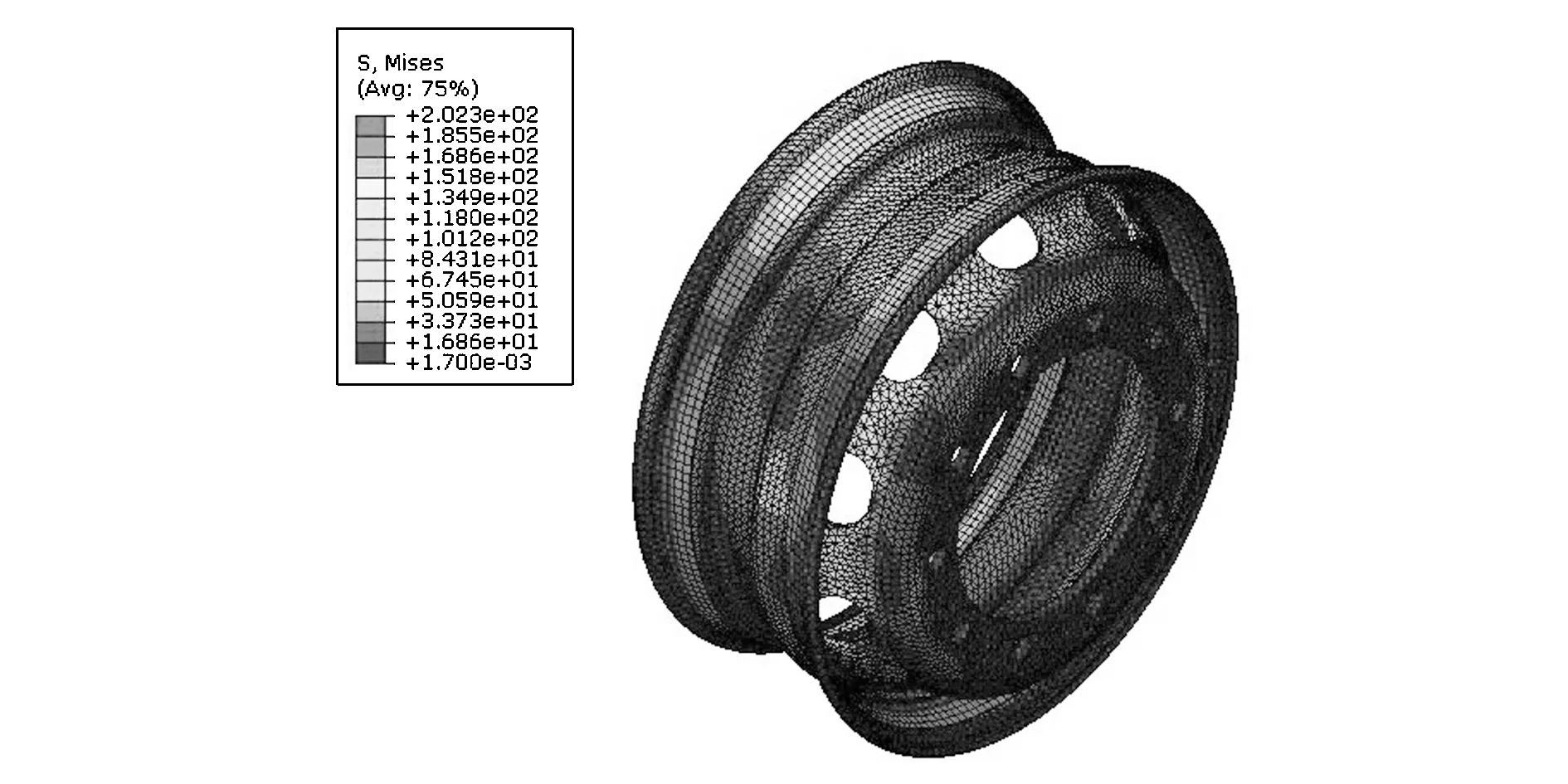
圖13 按新建載荷模型加載的仿真結果

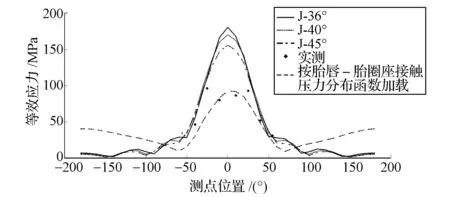
圖14 按胎唇-胎圈座接觸壓力分布函數進行加載得到的仿真結果與實測結果的對比

由圖14可見，按本文中所構建的胎唇-胎圈座間載荷模型進行加載，其仿真結果在高應力區域與實測應力吻合較好，雖然圖中沒有給出其它位置的實測應力，但因為仿真分析關注的是結構應力危險點的應力及疲勞壽命，因此并不會影響對車輪在徑向載荷作用下壽命的評估。采用胎唇-胎圈座接觸壓力分布函數，輪輞內側的應力在整圈中會出現兩個峰值；而采用J.Stearns理論進行加載，輪輞內側的應力在整圈中只有一個峰值。出現這種差異的原因是基于整圈實測壓強構建的載荷模型中包含正壓強和負壓強，正壓強對應有一個波峰，負壓強對應有一個波谷，又因為等效應力沒有負值，所以，在輪輞內側的等效應力在整圈會出現兩個峰值；而J.Stearns載荷模型中只有正壓強，對應一個波峰，因此，在輪輞內側的等效應力在整圈只有一個峰值。

4 結論

本文中針對車輪在徑向載荷作用下強度仿真結果不夠準確的問題，基于輪胎與輪輞間壓力分布的測試結果，構建了一種新的徑向載荷數學模型。通過與J.Stearns提出的余弦分布載荷加載下的車輪應力仿真結果與實測結果的對比，得出結論如下。

(1)按J.Stearns提出的余弦載荷形式進行車輪徑向載荷的加載，其仿真結果在高應力區域明顯偏大，導致基于該仿真結果進行車輪徑向疲勞壽命估算時過于保守，不利于車輪的輕量化設計。

(2)按所構建的胎唇-胎圈座間載荷模型進行加載，其仿真結果與實測結果在輪輞高應力區域吻合較好。這些為車輪壽命估算提供了更好的基礎，對鋼制車輪的輕量化設計具有重要的意義。

(3)胎唇、胎圈座間載荷分布在整圈范圍內有一個波峰和一個波谷，一個是正壓強的波峰，一個是負壓強的波谷，波峰和波谷的相位正好相差180°。

(4)采用所構建的胎唇-胎圈座間載荷模型，得到的輪輞內側的應力在整圈中會出現明顯的兩個峰值，而采用J.Stearns理論進行加載，輪輞內側的應力在整圈中只有一個明顯的峰值。因目前車輪應力測試時測點分布的角度范圍較小，今后將通過對輪輞整圈應力的測試對該現象進行進一步驗證。

[1]MohammedBillalK,ThomasOery,RaghuramanTaruvaiSankaran,etal.SimulationandTestCorrelationofWheelRadialFatigueTest[C].SAEPaper2013-01-1198

[2]MENGJin,ZHUPing,JIQinghui,etal.AnImprovedPressureDistributionModelofAutomotiveWheel'sRadialFatigue[J].AppliedMechanicsandMaterials, 2012, 201-202(10):287-291.

[3]RajuPRamamurty,SATYANARAYANAB,RAMJIK,etal.EvaluationofFatigueLifeofAluminumAlloyWheelsunderRadialLoads[J].EngineeringFailureAnalysis,2007,14(5) :791-800.

[4]MehmetFirat,RecepKozan,MuratOzsoy,etal.NumericalModelingandSimulationofWheelRadialFatigueTests[J].EngineeringFailureAnalysis, 2009,16( 5): 1533-1541.

[5]TOPACMM,ERCANS,KURALAYNS.FatigueLifePredictionofaHeavyVehicleSteelWheelunderRadialLoadsbyUsingFiniteElementAnalysis[J].EngineeringFailureAnalysis,2012,20:67-79.

[6] 韋東來，崔振山. 鋁合金車輪徑向疲勞試驗的數值仿真[J]. 機械強度，2008,30(6): 998-1002.

[7]WANGGuofeng,SUNHuixue,LIJian,etal.StudyonBiaxialFatigueLifeTestandFEAAnalysisoftheSteelWheel[C].InformationandComputing(ICIC), 2010ThirdInternationalConferenceonIEEE, 2010, 4: 235-237.

[8] 顏偉澤，郝艷華，黃致建，等.車輪徑向疲勞試驗有限元仿真及疲勞壽命估算[J].機械設計與制造，2011(6):54-59.

[9]STEARNSJ,SRIVATSANTS,PRAKASHA,etal.ModelingtheMechanicalResponseofanAluminumAlloyAutomotiveRim[J].MaterialsScienceandEngineering,2004,366(2): 262-268.

[10] 王偉，鄧濤，趙樹高. 輪胎與輪輞接觸的有限元分析[J]. 特種橡膠制品，2003，24(2):41-46.

[11] 薛小香，姚振漢，尹偉奇，等.子午線輪胎靜負荷實驗的有限元模擬[J]. 工程力學，2005，22(4): 33-42.

[12]LIUJunhui.ResearchonTire/wheelLoadDistributionofStructuralStrengthofSteelWheels[D].Beijing:BeihangUniv.,2012.

Modeling of the Contact Pressure Distribution Between the Tire Bead and Bead Seat of Vehicle Wheel

Shan Yingchun1,2, Liu Wanghao1,2, Liu Xiandong1,2& Wang Jiegong3

1.SchoolofTransportationSci. &Eng.,BeihangUniv. ,Beijing100191; 2.BeijingKeyLaboratoryforHigh-efficientPowerTransmissionandSystemControlofNewEnergyResourceVehicle,Beijing100191; 3.ShandongXingminWheelCo.,Ltd.,Longkou265716

The equivalent stresses in wheel rim obtained by a simulation based on the assumption proposed by J. Stearns that the distribution of contact pressure between tire bead and bead seat follows the cosine law are significantly deviated from test results. To resolve this problem, the contact pressure distribution between tire bead and bead seat is measured first and a curve of the change of distributed pressure caused by applying radial load on wheel rim is obtained. Then a novel contact pressure distribution model between tire bead and bead seat is built based on the fitting of that pressure distribution curve obtained. Finally a simulation is conducted on the new model built. The results show that with the new contact pressure distribution model built, an equivalent stress distribution in wheel rim closer to reality can be obtained.

steel wheel; tire bead; bead seat; contact pressure distribution; simulation

*北京市自然科學基金(3142013)和國家自然科學基金(51405011)資助。

原稿收到日期為2014年7月25日，修改稿收到日期為2014年9月12日。