道路載荷譜采集可靠度評判方法的研究與應用

曾發林，阮 洋，李建康

(1.江蘇大學汽車工程研究院, 鎮江 212013; 2.江蘇大學汽車與交通工程學院, 鎮江 212013)

2016015

道路載荷譜采集可靠度評判方法的研究與應用

曾發林1，阮 洋2，李建康1

(1.江蘇大學汽車工程研究院, 鎮江 212013; 2.江蘇大學汽車與交通工程學院, 鎮江 212013)

本文中對道路載荷譜采集可靠度的評判方法進行了研究。首先探討時域標準差參數與基于雨流計數法計算疲勞累積偽損傷值之間的關系,得出偽損傷值與標準差正相關的結論。然后基于以上結論,提出一種同車軸載荷譜歸一化標準差評判方法,并成功應用于載荷譜采集監測過程。最后通過載荷譜的雨流參數擬合,表明標準差也影響雨流變程和均值的分布性狀。本研究的結果表明:該方法理論意義清晰,具有提高載荷譜采集可靠性、節約試驗時間的工程應用價值,為后續室內道路模擬試驗奠定基礎。

道路載荷譜;歸一化標準差;雨流計數法;室內道路模擬試驗

前言

汽車耐久性工程中的關鍵是獲得可靠的載荷數據，而這些載荷數據必須能夠準確代表用戶實際使用過程中汽車零部件的累積損傷[1]。用于室內道路模擬試驗的目標道路載荷譜(下文簡稱載荷譜)的采集屬于隨機過程，其每個樣本中各對應元素時間歷程具有一定的離散性[2]。在汽車試驗場采集數據時，由于受到實際行駛車速的非平穩性、駕駛員的駕駛習慣、測量儀器的非線性失真和行駛環境中存在風阻、坡阻和慣性等因素影響[3]，使載荷譜信號具有非線性非平穩特征，嚴重情況下會導致在臺架試驗迭代環節出現結果發散、得不到合適驅動譜的問題。倘若后期才發現載荷譜存在瑕疵，補救方法有限，重新采集則嚴重浪費人力與物力。因此，實時監測載荷譜采集過程的可靠度和有效性顯得非常重要。

本文中通過仿真數據與工程實際載荷譜的計算分析，探究了樣本標準差S和基于雨流計數法算出的疲勞累積偽損傷值D(下文簡稱損傷D)之間的關聯性，首次提出同車軸載荷譜歸一化標準差評判法，并初步研究了針對載荷譜雨流參數分布模型的擬合問題。實際工程應用表明，本文中所述方法能夠提高數據采集的可靠度，具有較高的工程應用價值與指導意義。

1 參數計算介紹

1.1 雨流計數法簡介

雨流計數法屬于典型的雙參數法，雙參數分別為動強度(雨流域變程Range，相鄰峰谷值之差，兩倍于循環振幅)和靜強度(雨流域均值Mean，相鄰峰谷值的平均值)。最終計數所得的雨流矩陣記錄了三維數據——變程Range、均值Mean及相應頻次Cycle。文獻[4]～文獻[6]中對雨流計數法有詳細介紹，可概括為3步：

(1)將載荷譜的幅值范圍等級劃分后進行遲滯濾波，刪除不能構成損傷的小量變程循環；

(2)提取具有損傷性的子循環，統計Range、Mean和Cycle，形成雨流矩陣；

(3)根據預先設定的疲勞-壽命曲線和Miner線性疲勞累積損傷理論[7]來估算損傷值。

雨流計數法的統計結果能夠比較全面地反映載荷的真實特征，且主要應用于以下方面：

(1)刪除微小損傷循環，壓縮時域載荷譜以達到加速疲勞試驗的目的；

(2)通過雨流矩陣運算，外推出時程更長的載荷譜信號，克服某些強化路面距離短的不足；

(3)估算疲勞壽命和編制疲勞試驗載荷譜[8]；

(4)基于損傷等效原理，得到各強化道路路段的組合系數。

1.2 標準差計算

在實際處理中，一般平穩物理現象的隨機數據都可以認為是各態歷經的，所以能夠用單個樣本(時間歷程記錄)來測定其特征。道路載荷譜屬于隨機響應信號，具備不規則、不能重復等特征，須要使用統計分析方法對其進行描述與分析。因此，采用樣本標準差S作為總體標準差σ的估計值，計算公式[9]為

(1)

2 評判法提出的工程背景

載荷譜的采集過程中，一般只能進行短時間(距離)的采集。本文中主要研究兩組實測載荷譜，其中某型三軸重型運輸車的載荷譜采集于安徽定遠汽車試驗場(其典型軸頭加速度計安裝位置見圖1(a))，包括比利時路、搓板路等典型強化路面。行駛車速按照試車場的試驗標準進行，采樣頻率為400Hz，稱為1#道路載荷譜。另外，某型雙軸SUV車的道路載荷譜采集于湖北襄樊汽車試驗場(其典型軸頭加速度計安裝位置見圖1(b))，包括搓板路、長波路等強化路面，采樣頻率為200Hz，稱為2#道路載荷譜。

圖1 不同測試車型的典型位置加速度計安裝

1#道路載荷譜在后期的室內道路模擬試驗的迭代環節中，前軸左軸頭與后軸右軸頭在卵石路和扭曲路工況下的迭代結果無法收斂，延誤正常的臺架試驗進度。通過觀察扭曲路下的PSD(圖2)發現，前軸左軸頭和后軸右軸頭在3.0Hz以下低頻范圍內的能量比其他4個軸頭大得多，而其余各軸的主要能量集中在3.5和11.0Hz左右，進而斷定該兩軸頭傳感器在采集過程中受到干擾。若作3Hz低頻范圍的濾波處理，則違背了載荷譜編輯前后PSD需一致的原則[10]，并且無法全面地考察扭曲路況下的損傷效果。若在前期采集過程中及時發現問題，則可排除故障，避免物力的浪費。因此，運用一種簡捷有效的監測評判法顯得很有必要，基于時域參數計算方便的優點，著重考察時域均值μ、標準差S與損傷D的關系。

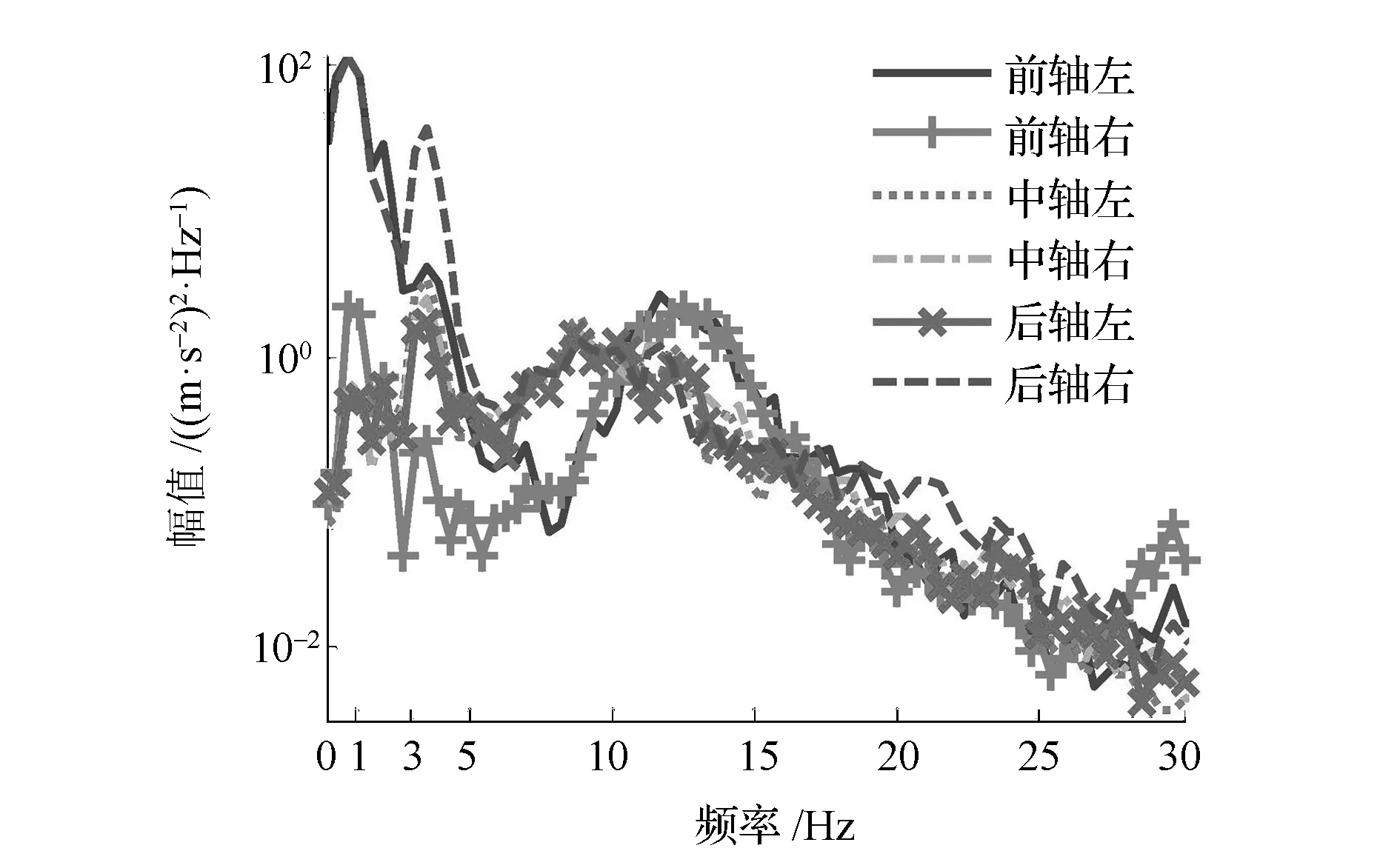
圖2 扭曲路工況下的載荷譜PSD計算結果

3 數值仿真

通過構造多組幅值服從正態分布的仿真隨機加速度信號，更改均值μ和標準差S兩個統計參數與損傷D之間的相關性。設所有仿真信號的采樣頻率為500Hz，總采樣時間為4s。

3.1 時域均值與損傷的關系

第一組仿真加速度信號的均值μ變化范圍為0～200m/s2，增幅為10m/s2，標準差S統一為1m/s2。為方便統計，將損傷D與μ進行歸一化(圖3)，發現μ與損傷的關聯性不是很有規律，非線性特征很強，意味著μ對最終損傷計算的影響不大。每組仿真信號的疲勞循環統計總數基本上在650次左右。

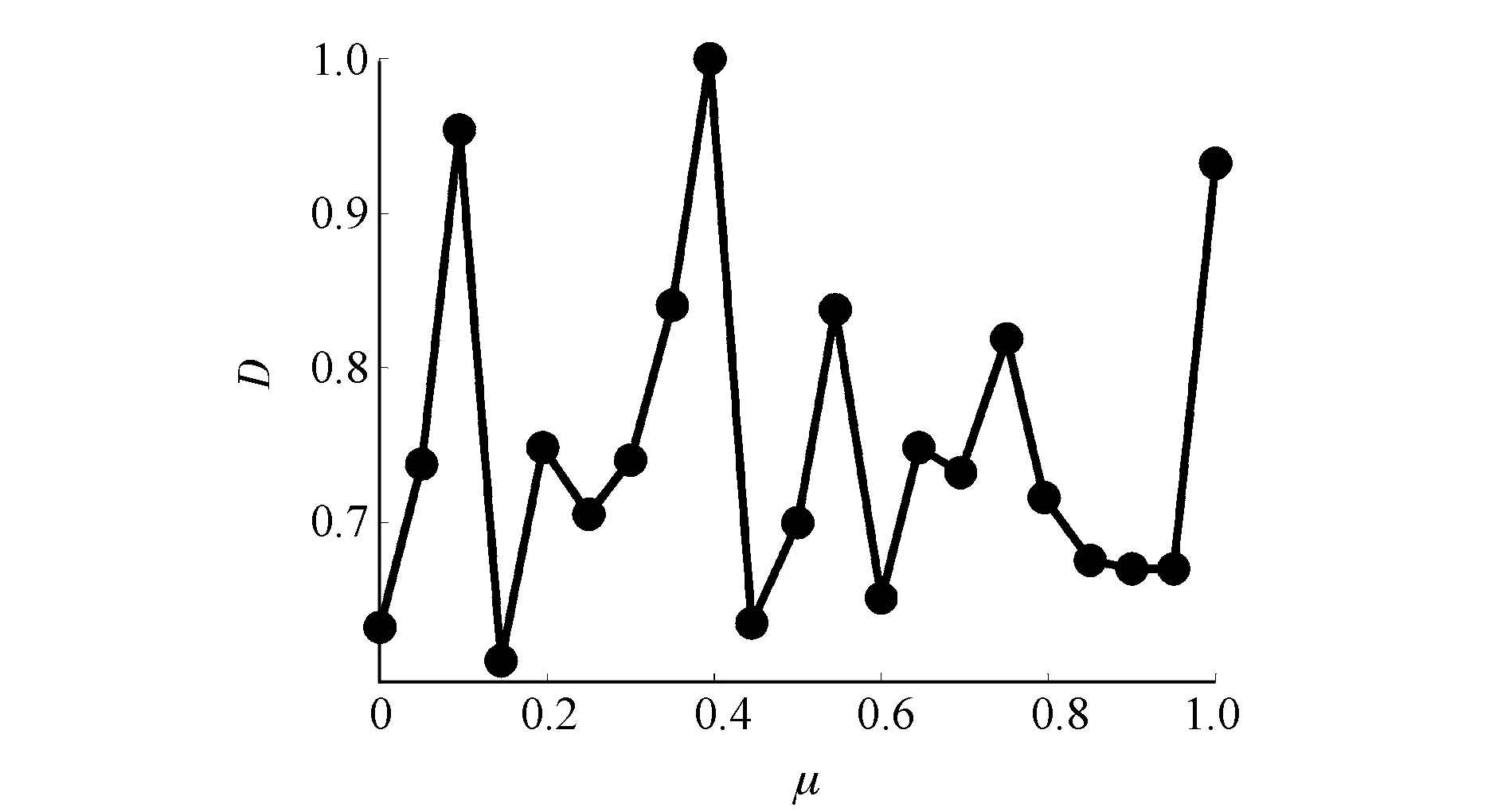
圖3 時域均值μ與損傷D的關系曲線

同時，觀察雨流矩陣的形狀圖(圖4)可發現，Mean具有以μ為對稱軸進行分布的特征。在編制特定疲勞載荷譜時(如隨機非各態歷經過程載荷譜)，須要考慮Mean的影響。

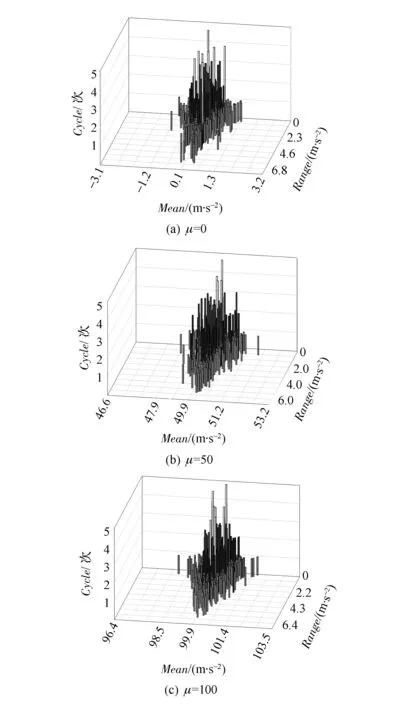
圖4 典型仿真信號雨流矩陣

3.2 標準差與損傷的關系

第二組仿真數據的標準差S取值范圍為0～200m/s2，增幅為10m/s2，時域均值μ統一為0。仿真結果表明：幅值服從正態分布的隨機信號，其疲勞循環數基本保持不變，并且S和D在雙對數坐標下呈現線性關系(線性坐標下為冪函數形式)，設定擬合公式為

D=ea·Sb或lnD=a+blnS

(2)

式中:a和b為待定參數，擬合結果見圖5。文獻[11]中指出，描述材料疲勞-壽命曲線的最常用形式就是冪函數形式，則待定參數a和b應與材料性質、應力比、加載方式等因素有關。

通過相關系數r[11]可判斷變量x與y之間的線性相關程度，r由偏差乘積和Lxx，Lyy，Lxy定義，即

(3)

r的絕對值越接近1，表明兩參數的線性相關程度越強。經計算，在雙對數坐標下的D-S線性相關系數達到0.999 9，線性相關程度很高，說明擬合公式正確合理。

圖5 時域標準差S與損傷D關系曲線

4 評判法的具體內容

4.1 初步假設

先作假設：

(1)不同路況采集所得的載荷譜可以看作是各態歷經的穩態隨機過程；

(2)車輛可以理想為對稱結構，且左、右車轍的路面不平度系數相等[12]，同軸的左右兩個軸頭結構、配重和力學性能參數相似。

基于以上兩點假設，同軸軸頭載荷譜除存在相位差的可能性之外(如扭曲路)，兩者的標準差S與損傷值D應該處于同一量級水平。因此，可將二者載荷譜的S與D同時作歸一化處理。譬如，若前軸的左軸頭載荷譜標準差大于右軸頭，則將左軸頭載荷譜標準差歸一化為100%。同一強化路面下時間序列樣本的選取、比較、分析，應遵循具有相等時間長度的原則。

將1#道路載荷譜在各路況下作歸一化S和D計算，見圖6(限于篇幅，不通過列表形式給出詳細計算結果)。結果表明，在各強化路面下，D與S存在正相關關系，意味著如果某軸頭載荷譜的S值大于另一軸頭，那么其D值必定相對較大。同時，圖6存在兩個歸一化比列不協調的異常現象：

(1)在卵石路工況下，前軸右軸頭載荷譜歸一化S值為71.08%(后軸左軸頭歸一化S值為66.00%)，而其歸一化D值為32.45%(后軸左軸頭歸一化D值為23.82%)；

(2)在扭曲路工況下，前軸右軸頭載荷譜歸一化S值為28.04%(后軸左軸頭載荷譜歸一化S值25.02%)，歸一化D值為1.42%(后軸左軸頭歸一化D值為0.52%)。

圖6 某運輸車載荷譜歸一化S和D計算結果

通過圖6可以初步判斷在這兩種路況下，前軸和后軸必定存在某個軸頭的載荷譜采集存在問題(由第2節已知前軸左軸頭和后軸右軸頭信號采集有誤)。

4.2 標準差同雨流計數法的聯系

從3.2節和4.1節的內容，總結出一個普遍規律：偽損傷D正相關于時域標準差S，即D∝S。從概率意義理解，S值越大，即載荷譜的幅值越離散，則經雨流計數得到大變程循環的可能性就越大，從而得到更高的偽損傷值。S計算過程比D計算過程更為簡捷，且易于編程，省去雨流計數再計算損傷的繁瑣過程。

名義上各試驗路段每一循環的載荷是一樣的，實際上不可能完全一致，因此在理論上為了精確地獲得載荷譜的平均值，須要進行無限次測量，但明顯不現實。如何在有限的采集循環里，提高采集可靠度很有工程意義。基于以上分析，提出“同車軸載荷譜歸一化標準差評判法”，根據S值的大小來判斷各類型載荷譜損傷，嘗試用于實時監測道路載荷譜的現場采集過程中，進而判斷信號采集的正常與否。當某同車軸的兩軸頭所測載荷譜的歸一化S值小于某一閾值時，則說明在該強化路況下的采集存在問題，有必要重新采集，避免整個采集循環失效。因為受到測量車輛、路面參數等眾多因素的影響，該閾值的設定具有不確定性，建議取值不可低于75%，具體取值需要更多的工程經驗加以確定。

4.3 評判法的應用工程實例

應用本文中“同車軸載荷譜歸一化標準差評判法”，實時監測2#道路載荷譜的采集試驗。通過實時計算歸一化標準差值，并規定閾值為78%，監測各強化道路載荷譜的采集情況。最終所測載荷譜正常，某一采集循環的計算結果見圖7(后期增補歸一化D值)，并且在后期的臺架試驗迭代環節中未出現任何問題，表明本文中的方法取得良好效果。表1為某SUV道路載荷譜時域統計參數和雨流域損傷計算結果。它驗證了在任何強化道路上，損傷D與標準差S正相關的結論。

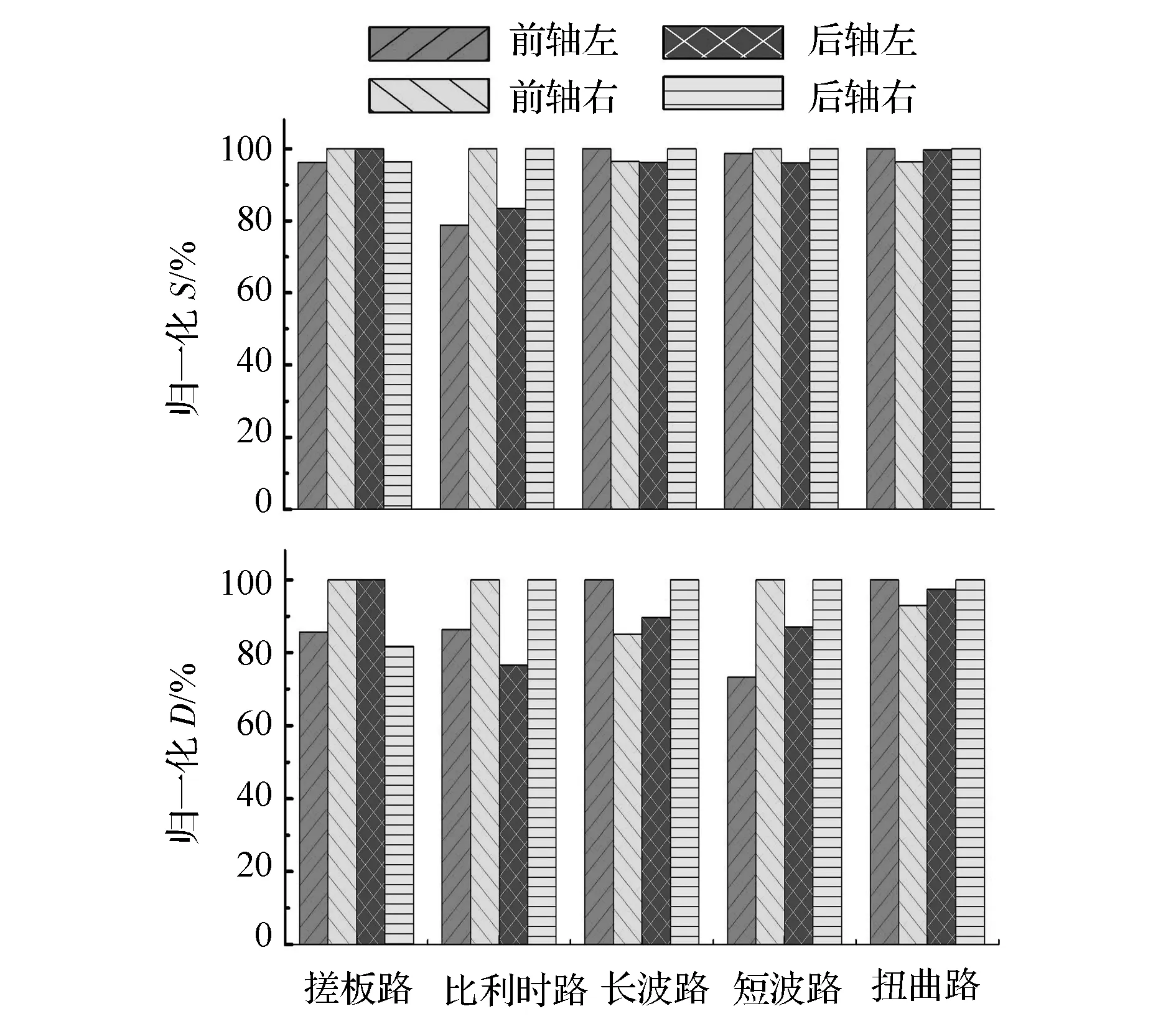
圖7 某SUV載荷譜歸一化S和D計算結果

5 雨流參數擬合

在同一道路載荷譜時間序列當中，假設信號為穩態隨機信號，即時域均值μ和標準差S不隨時間變化，那么通過雨流計算之后的偽損傷值只與S存在正相關的關系。應用雨流計數法完成對載荷譜的頻次統計，對得到的特征參數樣本——雨流Range和Mean進行概率分布擬合，找出描述參數分布特征的最佳模型。在無先驗經驗的情況下，通常選取6種常用分布模型——指數分布、正態分布、對數正態分布、Gamma分布、兩(三)參數Weibull對樣本進行擬合[13]。根據工程經驗，載荷譜的雨流域幅值一般服從正態分布或Weibull分布，雨流域均值服從正態分布。本文中，時域信號的差別通過S識別，雨流域Range和Mean的差別嘗試通過多級正態分布函數擬合識別。

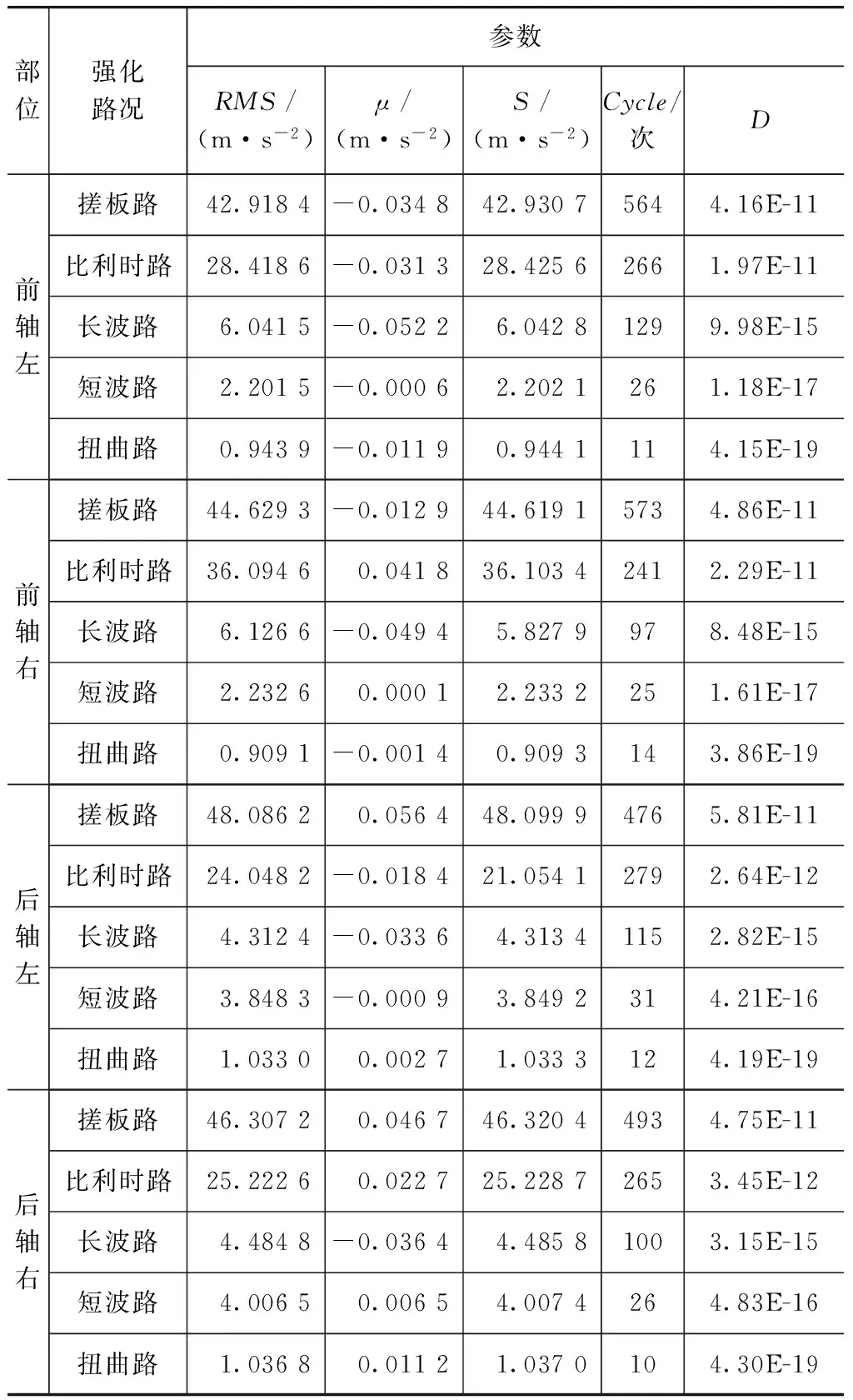
表1 某SUV道路載荷譜時域統計 參數、雨流域損傷計算結果

以某運輸車在扭曲路工況下的前軸載荷譜分析為例，左軸頭和右軸頭載荷譜的S值分別是12.671 4和3.552 6m/s2，時域均值μ分別是-0.344 9和0.000 8m/s2，Range和Mean的擬合結果見圖8。應用95%置信區間概率圖法進行假設檢驗，發現數據與多級正態分布組合的最佳擬合線最為接近，擬合誤差之和接近于零。對比圖8(a)和圖8(c)可知，左軸頭載荷譜的雨流變程范圍明顯大于右軸頭，且前者頻次分布主要集中在0～20m/s2，而后者集中于0～10ms2。同時，右軸頭雨流均值分布形狀(圖8(d))的對稱性要優于左軸頭(圖8(b))。表明標準差S的差異，折合到雨流域，則會影響參數Range和Mean的分布形狀。

圖8 扭曲路工況下前軸載荷譜雨流統計直方圖

針對SUV車，以分析搓板路工況下的前軸左軸頭載荷譜為例，其功率譜密度函數(圖9(a))存在38.8和78.1Hz兩個峰值，具有雙峰譜特征。文獻[14]中假設雙峰譜密度的雨流幅值(變程)分布可由兩個Weibull分布組合，而本文中通過實際檢驗，雙峰譜雨流變程可分為兩個正態分布的組合(圖9(b))，且雨流均值需要多個正態分布組合(圖9(c))。因為實測載荷譜具有非線性非平穩特征，所有的分布函數擬合只存在理論上的近似，可以肯定的一點是，雨流參數的分布形狀與標準差有關聯。針對不同路況下載荷譜雨流域Range和Mean的擬合研究，可以指導疲勞載荷譜的編制，限于篇幅原因本文中不作深入探究。

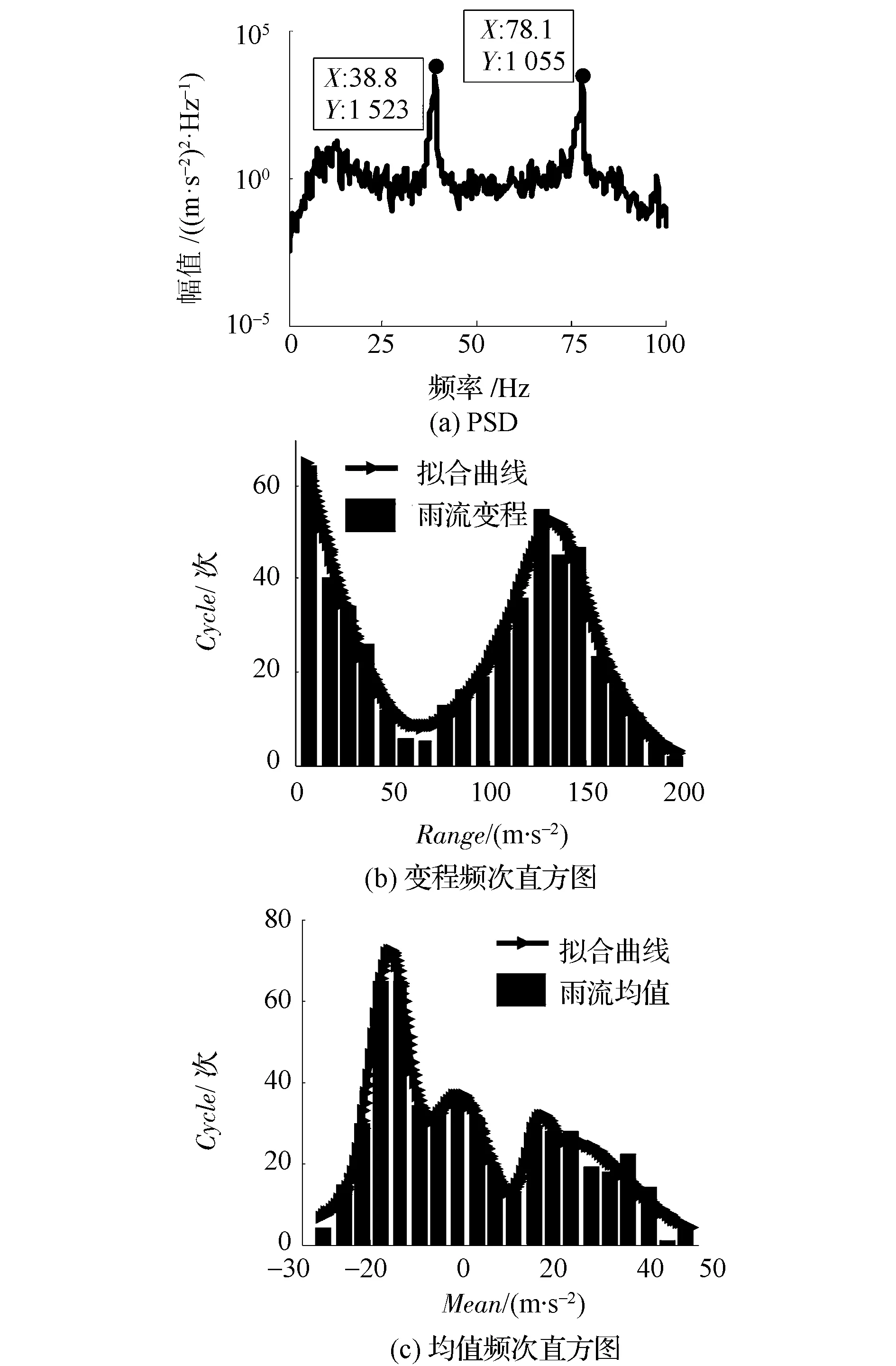
圖9 搓板路工況下載荷譜各參數計算結果

6 結論與展望

本文中采用同車軸載荷譜歸一化標準差評判法，實時監測道路載荷譜采集，可以提高采集的可靠度，避免人力物力的浪費，為后期臺架試驗的順利完成奠定基礎。該方法簡單高效，實際應用表明其含義直觀，使用方便。

(1)正態隨機仿真信號的分析結果表明，其標準差與疲勞累積偽損傷值呈對數線性關系；結合實測載荷譜信號的分析結果，得到更為一般的結論，即載荷譜的損傷值與標準差正相關。

(2)通過將不同強化路況下的載荷譜標準差作歸一化處理，設定歸一化閾值，當同軸載荷譜出現小于閾值時，基本可斷定該路況下的采集存在問題，須重新采集。

(3)載荷譜雨流域變程和均值的頻次分布特征受標準差的影響，且可由多級正態分布函數進行擬合。

關于歸一化S閾值的具體設定等問題，有待更多的道路載荷譜采集試驗來驗證，且時域標準差與雨流域雙參數之間的理論關系，需要大量的工程試驗數據進行更為深入的探究。最終，通過理論體系的完善來推廣該方法的應用。

[1] 康強,左曙光,周煒.汽車用戶道路行駛載荷譜測量及推斷方法研究[J].汽車技術,2009(10):55-58.

[2] 張覺慧,金鋒,余卓平.道路模擬試驗用載荷譜樣本選擇方法[J].汽車工程, 2004, 26(2): 220-223.

[3] 宋勤,姜丁,趙曉鵬,等.道路模擬試驗載荷譜的采集、處理與應用[J].儀表技術與傳感器,2011(3):104-106.

[4] 高鎮同,熊峻江.疲勞可靠性[M].北京:北京航空航天大學出版社,2000.

[5] CARMEN C, ENRIQUE C, CANTELI, et al. Rainflow Analysis in Coastal Engineering Using Switching Second Order Markov Models[J]. Applied Mathematical Modelling,2012,36(9):4286-4303.

[7] WANG Y S, MA Q H, ZhU Q, et al. An Intelligent Approach for Engine Fault Diagnosis Based on Hilbert-Huang Transform and Support Vector Machine[J]. Applied Acoustics,2014,75(1):1-9.

[8] 唐浩,屈梁生.基于支持向量機的發動機故障診斷[J].西安交通大學學報,2007,41(9):1124-1126.

[9] MANIKANDAN J, VENKATARAMANI B, AMUDHA V. A Noval Technique for Support Vector Machine Based Multi-class Classifier[C]. TENCON 2008. Hyderabad India:TENCON 2008 IEEE Region 10 Conference Publication,2008:1-6.

[10] 連可,黃建國,王厚軍,等.一種基于遺傳算法的SVM決策樹多分類策略研究[J].電子學報,2008,36(8):1502-1507.

[11] 王一,楊俊安,劉輝.一種基于遺傳算法的SVM決策樹多分類方法[J].信號處理,2010,26(10):1495-1499.

[12] 張慶,劉丙杰.基于PSO和分組訓練的SVM參數快速優化方法[J].科學技術與工程,2008,8(16):4613-4616.

[13] 金晶,王行愚,羅先國,等.PSO-ε-SVM的回歸算法[J].華東理工大學學報(自然科學版),2006,32(7):872-875.

Study and Application of the Reliability Evaluation Method for Road Load Spectra Acquisition

Zeng Falin1, Ruan Yang2& Li Jiankang1

1.AutomotiveEngineeringResearchInstitute,JiangsuUniversity,Zhenjiang212013;2.SchoolofAutomotiveandTrafficEngineering,JiangsuUniversity,Zhenjiang212013

The reliability evaluation method of road load spectra acquisition is studied in this paper. Firstly, the relationship between the standard deviation (SD) parameters in time domain and the cumulative fatigue pseudo damage calculated by rainflow counting algorithm is investigated with a conclusion that there is a positive correlation between pseudo damage and SD. Then based on the conclusion, an evaluation method of normalized SD of coaxle load spectra is proposed and successfully applied to the monitoring process of load spectra acquisition. Finally the rainflow parameter fitting of load spectra show that the SD also affect the distribution pattern of rainflow range and mean. The results of the study indicate that the method proposed is clear in theoretical sense and has the engineering application value in enhancing the reliability of load spectra acquisition and saving test time, laying the fundamentals for the follow-up indoor road-simulation tests.

road load spectra; normalized standard deviation; rainflow counting; indoor road simulation test

原稿收到日期為2014年4月2日，修改稿收到日期為2014年9月12日。