*-素環上同態或反同態的廣義導子

劉雙雙

(吉林師范大學 研究生院,吉林 長春 130103)

?

*-素環上同態或反同態的廣義導子

劉雙雙

(吉林師范大學 研究生院,吉林 長春 130103)

摘要：R是2-扭自由*-素環，J是R的非零*-Jordan理想.F是R上具有非零伴隨導子d的廣義導子.若F(xy)=F(x)F(y)或F(xy)=F(y)F(x)，x,y∈J,有d=0或R具有交換性.

關鍵詞：*-素環;*-Jordan理想;導子;廣義導子

0引言

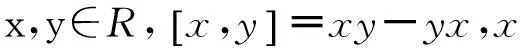
Bell 和Kappe[4]證明了若素環R的導子d在R的非零理想上是同態或反同態，則在R上d=0.近期，Asma et al[1]得到素環的Lie理想上的這一結果.另外，Yenigul ,Argac[7]和Ashraf[2]分別在素環的σ-導子和素環的(σ，τ)-導子上證明了的上述結果.Asma Ali和Deepak Kumar[5]將這一結果推廣到素環的廣義(θ，Φ)-導子上.

本文中，我們將這一結果推廣到*-素環上*-Jordan 理想的廣義導子上.

本文將用到下面的基本交換子恒等式，：

1主要結果

引理1[[6]引理2]R是2-扭自由*-素環，J是R的非零*-Jordan理想.若aJb=a*Jb=0， 則a=0或或b=0.

引理2[[7]引理3]R是2-扭自由*-素環，J是R的非零*-Jordan理想.若J?Z(R),則R具有交換性.

引理3[[8]引理2.6]一個群不能是它的兩個真子群的并.

定理1R是2-扭自由*-素環，J是R的非零*-Jordan理想.可加映射F:R→R

是具有伴隨導子d的廣義導子.

(i)若F是J上的同態映射，則d=0；

(ii)若F是J上的同態映射，則d=0或R具有交換性.

證明：(i)若F是J上的同態映射，

有F(xy)=F(x)y+xd(y)=F(x)F(y) x,y∈J

(1)

而F(xyz)=F(xy)z+xyd(z) x,y,z∈J

(2)

F(xyz)=F(x)F(yz)=F(x)F(y)z+F(x)yd(z)x,y,z∈J

(3)

比較(2)(3)得(F(x)-x)yd(z)=0 x,y,z∈J，即(F(x)-x)Jd(z)=0

用z*替代z得到(F(x)-x)Jd(z*)=0，而*與d可交換，則

(F(x)-x)Jd(z)*=0

由于R是*-素環，由引理1得F(x)-x=0或d(z)=0.當F(x)=x時，

xy=F(xy)=F(x)y+xd(y)x,y∈J

由上式得到xd(y)=0，i.e.Jd(y)=0.由于J≠0,所以d(y)=0 y∈J.

綜上所述，d=0

(ii)若F是J上的同態映射，有F(xy)=F(x)y+xd(y)=F(y)F(x) x,y∈J

(4)

在(4)中用xy代替x，得到xyd(y)=F(y)xd(y) x,y∈J

(5)

在(5)中用zx代替x，得到zxyd(y)=F(y)zxd(y) x,y,z∈J

(6)

用z左乘(5)得到zxyd(y)=zF(y)xd(y) x,y,z∈J

(7)

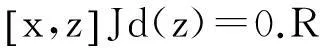
綜上所述，d=0或R具有交換性.

參考文獻：

[1]Bell HE,Kappe LC.Rings in which derivations satisfy certain algebraic conditions[J],Acta.Math.Hungar,1989,53:339-346.

[2]Ali A,Rehman N,Shakir A.On Lie ideals with derivations as homomorphisms and anti-Homomorphisms[J].Acta Math.Hungar,2003,101:79-82.

[3]Yenigul M,Argac N.On prime and semiprime rings with α-derivation[J].Turk.J.Mah,1994,18:280-284.

[4]Ashrsf M,Rehman N,Quadri M A.On (σ，τ)-derivations in certain classes of rings[J].Rad.Mat,1999,9:187-192.

[5]Asma Ali,Deepak Kumar.Generalized derivations as homomorphisms or as anti-homomor-Phism in a prime ring[J].Hacettepe Journal of Mathematics and Statistics Volume,2009,38:17-20.

[6]Oukhttite L,Salhi S,Taoufip L.Commutativity conditions on derivations and Lie ideals in σ-prime rings[J].Beitrage Algebra Geom,2010,51:275-282.

[7]Oukhtite L.On Jordan ideals and derivations in rings with involution[J].Comment.Math.Univ.Carolin,2010,51:389-395.

[8]Huang S.Generalized derivations of prime rings,International Journal of Mathematics and Mathematical Sciences[J],Article ID,2007,6:85612.

[責任編輯：王軍]

Generalized derivation of the homomorphism or anti-homomorphism on *-Prime ring

LIU Shuangshuang

(Graduate School,Jilin Normal University,Changchun 130103,China)

Abstract:In the present paper it is shown that:if R is 2-torsion free *-prime ring,J be a nonzero *-Jordan ideal.F is called a generalized derivation associated with a derovation d.If Either F(xy)=F(x)F(y)or F(xy)=F(y)F(x) for all x,y∈J,then d=0or R is commutative.

Key words:*-prime ring;*-Jordan ideal;derivation;generalized derivation

中圖分類號：O153.3

文獻標識碼：A

文章編號：1672-3600(2016)03-0022-02

作者簡介:劉雙雙(1990-)，女，滿族，吉林長春人，吉林師范大學碩士研究生，主要從事環論的研究.

收稿日期：2015-11-17