基于分數階傅里葉變換的高動態目標檢測方法

黃明軍，王永民，牛家紅

(空軍工程大學信息與導航學院，陜西 西安 710077)

?

基于分數階傅里葉變換的高動態目標檢測方法

黃明軍，王永民，牛家紅

(空軍工程大學信息與導航學院，陜西 西安 710077)

摘要:針對高動態環境下接收機的接收信號含有較大多普勒頻率及其變化率，傳統捕獲方法無法對多普勒頻率變化率進行有效補償的問題，提出了基于分段自相關分數階傅里葉變換的高動態目標檢測方法。該方法首先對接收信號進行載頻預測，將接收信號調制到基帶信號，然后利用分數階傅里葉變換對線性調頻信號在最優階次具有能量聚集的特點，采用分段自相關與離散分數階傅里葉變換相結合的處理方法，快速而準確的估計出多普勒頻率及其變化率。仿真驗證表明，該方法解決了傳統方法在高動態環境下難以對信號多普勒變化率進行有效補償的問題，并提高了檢測信噪比和接收機捕獲概率。

關鍵詞:高動態；捕獲；線性調頻；分數階傅里葉變換；檢測

0引言

直接序列擴頻體制在測控、通信和導航等領域中有著廣泛的應用，但擴頻技術的廣泛應用是以準確同步為前提的。航天測控中，由于飛行器離地面站較遠，且飛行速度高，接收信號的能量微弱同時還具有較高的多普勒頻率變化率，因而高動態環境下偽碼快速捕獲是實現飛行器測控的關鍵因素。

偽碼捕獲方法眾多，當前多使用并行快速傅里葉變換(Fast Fourier Transform，FFT) 的方法進行捕獲，它的一大優點是捕獲速度快，如文獻[1—3]所提出的方法。基于 FFT方法在頻域進行捕獲時，不僅會引起由于時域截斷而產生的能量泄漏和分析點個數有限而帶來的扇貝損失[4]，而且在高動態環境下由于載體高速運動使信號產生了較大多普勒頻率，并伴有較大多普勒頻率變化率，這些捕獲方法難以對由加速度引起的多普勒頻率變化率分量進行有效補償[5]。因而，傳統捕獲方法在高動態環境下并不適用，尤其是對捕獲準確性要求較高的場合下。針對此問題，本文在文獻[6]的基礎上，提出了一種基于分段自相關分數階傅里葉變換的高動態目標檢測方法。

1分數階傅里葉變換技術

在衛星移動通信與深空測控通信等高動態環境下，由于載體的機動范圍和機動強度很大，使得發射信號的多普勒頻移、一次變化率、甚至二次變化率都比較大，使信號參數發生強烈變化。當多普勒頻移達到±25 kHz時就對信號捕獲時頻域的搜索帶寬提出了較高要求，頻域帶寬增加，使得頻域搜索點個數增加，數據處理量增大[7]；另外，由于頻率變化率的存在，使得載波頻偏不再是一個恒定不變的常數，這就給偽碼快速捕獲帶來了困難，使得傳統捕獲方法不再適用于高動態環境。

設在高動態環境下，載波頻偏表示為fd(t)，將其進行泰勒級數展開，則表為:

(1)

由于頻率變化率k的存在，導致多普勒頻率不斷變化，因此在一段觀測時間內信號不能看作頻率不變的信號，信號離散傅里葉變換頻譜也不再是一個單峰譜，而是由高動態性引起的擴展頻譜，離散傅里葉變換是不適用的。圖 1中可以明顯看到信號傅里葉變換頻譜能量無法集中，不再出現單峰，而是出現頻譜擴展現象，無法進行頻偏估計。因此，高動態環境下，傳統利用FFT估計頻偏的效果并不理想。基于此，在高動態環境下，現階段將分數階傅里葉變化技術(FRFT)引入到了偽碼捕獲算法當中。

分數傅里葉變換理論是在傳統傅里葉分析的基礎上迅速發展起來的一門新興學科。傅里葉變換的基函數是一族指數函數{ejwt}，因此，傅里葉變換適合分析平穩信號，對現實物理世界中的多數非平穩信號是不適用的。在時頻平面中，時間軸與頻率軸相互垂直，即認為傅里葉變換將信號從時間域旋轉π/2變換到頻率域。如果將時頻平面旋轉不是π/2的整數倍角度時，信號在這個域的表示則由分數階傅里葉變換給出，這個域稱為分數階傅里葉變換域[8]。

根據文獻[9]，信號s(t)在旋轉角度α下的FRFT表示為：

(2)

其中，p是FRFT的階數，p=2α/π，變換核

(3)

圖1　高動態對捕獲性能影響Fig.1　Capture high dynamic impact on performance graph

圖2給出了Chirp信號的FT和FRFT示意圖。Chirp信號在時頻平面上呈斜刀刃狀，具有明顯的時頻耦合特性。Chirp信號的FT可以看作是其在頻率軸f上的投影，較寬的頻譜使得能量分散；而FRFT則是在旋轉角度α后u軸上的投影。隨著旋轉角度在[0,π]范圍內變換，分數階Fourier變換展示出信號從時域逐步變化到頻域的所有變化特征，可以為信號時頻分析提供更大選擇余地；從物理意義上講，FRFT就是將信號在時頻平面的任意旋轉。從上式可以看出，當旋轉角度為0時，即是信號本身，旋轉角度為π/2時信號FRFT變換就是其頻域特征，合適的旋轉角度α可以使Chirp信號的能量高度集聚，產生一個很窄的積累峰值，利于對信號的檢測與估計，這一性質在對LFM信號的處理中具有很大優勢。

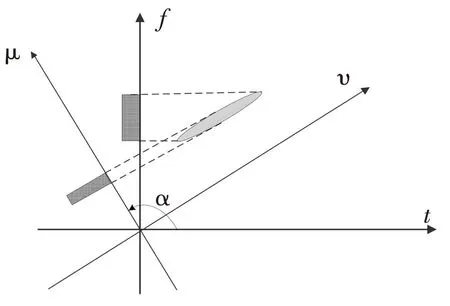
圖2　LFM信號的Fourier變換與FRFT比較Fig.2　Compare Fourier transform and FRFT on LFM signal

2分段自相關FRFT的高動態目標檢測原理

由1知，傳統捕獲方法無法檢測出多普勒頻率變化率的補償量，因而不適合高動態環境下信號的快速捕獲。基于此，本文提出了分段自相關與分數階傅里葉變換相結合的高動態目標檢測方法，有效估計了多普勒頻率變化率。所提方法先通過FFT對信號載頻預測，減小頻偏變化區間，再通過部分匹配濾波器(PMF)近一步降低數據處理量，大大減小了捕獲時間，最后利用FRFT對調頻信號有能量聚積的特性，通過檢測峰值來估計多普勒變化率分量。具體實現如圖3所示。

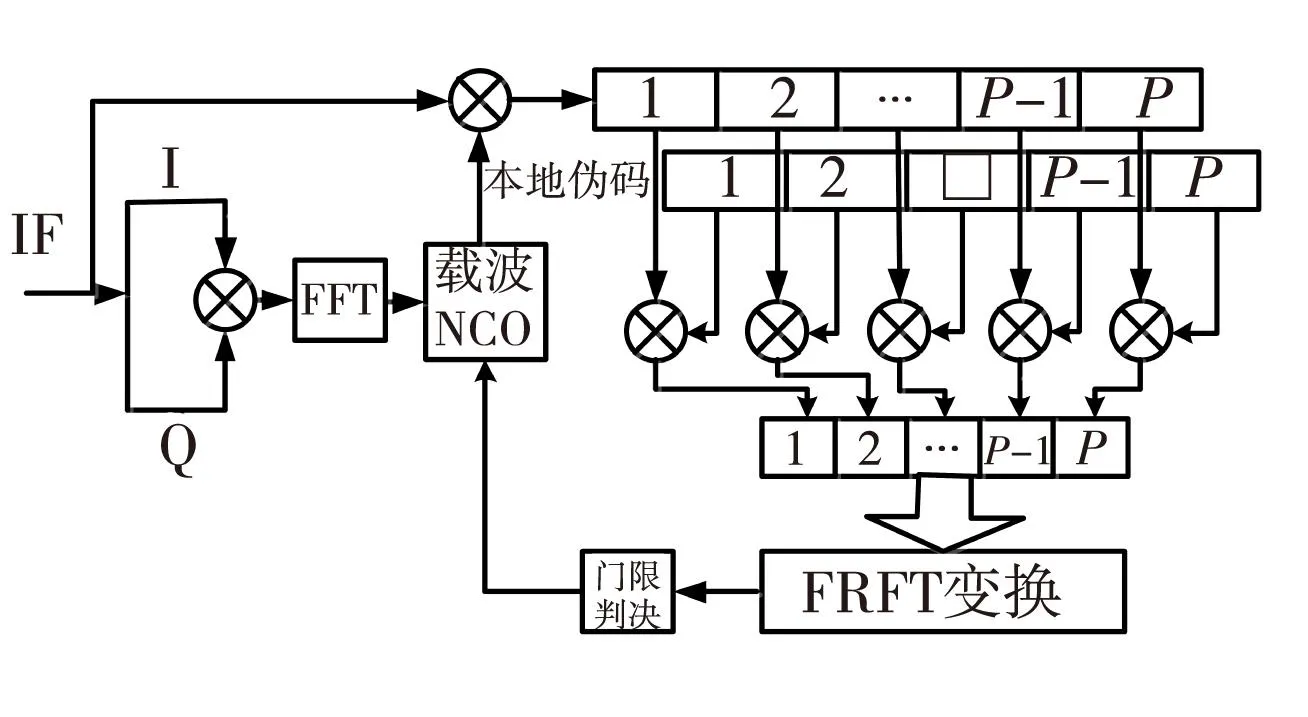
圖3　F-PMF-FRFT系統原理圖Fig.3　Schematic of F-PMF-FRFT System

從系統的原理框圖可以看出，本文所提算法主要包括三個步驟：第一，對接收到的中頻信號分為I和Q路并分別相乘，對相乘后的信號進行FFT變換，預測多普勒頻偏，然后進行混頻，得到基帶信號；第二步，對基帶信號進行部分相關降采樣，得到P個相關值；最后，對這P個相關值進行FRFT搜索，利用chirp信號在合適角度出現能量聚集的特性得到相關峰值并與門限值比較，估計出殘余多普勒頻偏fd′和頻率變化率k。由此可見，該方法能夠通過檢測峰值估算出多普勒頻移及其變化率分量，從而進一步實現偽碼捕獲。

設高動態下接收到的信號為：

(4)

由式(1)、式(4)得：

(5)

則混頻后的零中頻信號為：

(6)

假設偽碼已經同步，則混頻后的零中頻信號為：

(7)

經過數字化采樣后，可得

(8)

其中m=1,2,3,…,M-1，M為抽樣后的點數。

每個單元信號可以表示為：

(9)

其中p=0,1,2,…,P-1,n=1,2,…,N-1。

分別對P個單元進行相干積累，得到的P個相干積累值為：

(10)

其中，B=A·exp(j(2πpNfd′/fs+πkp2N2/fs2+φ))

根據文獻[10]中離散時間分數階傅里葉變換的定義，序列x(n)可在p階分數階傅里葉域數字頻率軸上表示為：

(11)

根據這種算法，離散信號關于alpha的N點DFRFT可表示為[11]：

(12)

聯合式(10)、式(11)、式(12)得到

sk(α,m)=AαP-1/2·

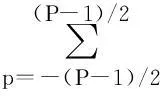
p2cotα)/P]·A·

exp(j(2πpNfd′/fs+πkp2N2/fs2))·

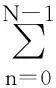
2nfd′/fs+2kpNn/fs2]}·

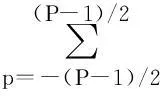
p2(cotα/P+2kN2/fs2)]}

(13)

當-2mcscα/P+2Nfd′/fs=0,cotα/P+kN2/fs2=0時，sk(α,m)值最大，此時信號在分數階傅里葉域具有最好能量聚集性，出現明顯的峰值，通過對sk(α,m)在(α,m)平面做峰值搜索得到與LFM信號對應得峰值坐標(α,m)，基于此對信號頻偏差和頻率變化率進行估計。

(14)

3仿真驗證及性能分析

為了分析上述算法在高動態環境下的捕獲性能，本文采用觀測時間Tp=4 s,擴頻碼長度為4096的擴頻系統，輸入均值為0、信噪比SNR=-20 dB的加性高斯白噪聲，預測后的多普勒頻偏差為100 Hz，多普勒頻率變化率為100 Hz/s，fs=1 000 Hz,P=128，N=32的性能指標使用 MATLAB進行仿真，仿真結果如圖4所示。

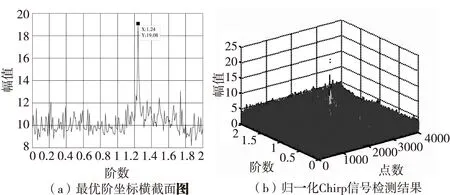
圖4　F-PMF-FRFT系統仿真圖Fig.4　Simulation diagram of F-PMF-FRFT system

由于Chirp 信號在相應階次的分數階傅里葉域內能實現能量聚集，高斯噪聲在任何分數階傅里葉變換域都呈現高斯形狀，在分數階傅里葉域上高斯噪聲不具有很好的時頻聚焦性，因而，圖4出現了明顯峰值，易于信號的檢測與參數估計。由圖4可以看出，峰值對應的二維平面坐標值為p0=1.24。由此可推得：實際信號的參數估計為k=98.98 Hz/s，fd=99.95 Hz。通過計算可得頻率的估算誤差為：(100-99.95)/100=0.05%，頻率變化率的估算誤差為：(100-98.98)/100=1.02% 。

通過仿真系統在不同信噪比時高動態目標參數估計、不同分數階次步長Δp時高動態目標參數估計、不同分段匹配濾波器個數P時高動態目標參數估計得到表1-表3。

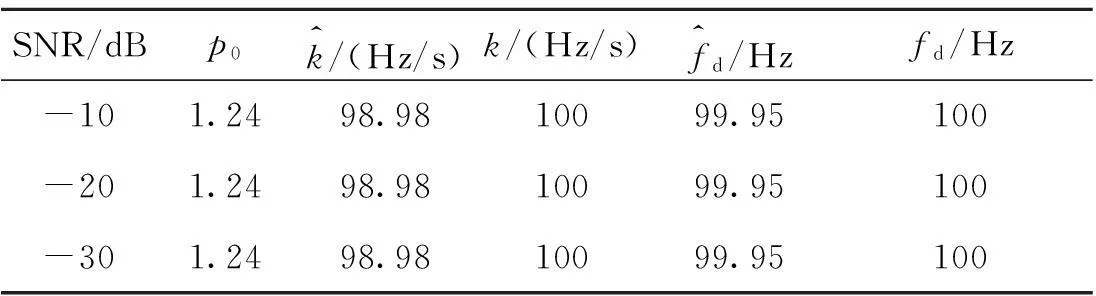
表1　不同信噪比時高動態目標參數估計

表1給出了分數階次步長Δp=0.01，分段匹配濾波器個數P=128條件下，不同信噪比時高動態目標參數估計情況。由表1可知，當SNR為-10 dB、-20 dB和-30 dB時，由于目標峰值明顯高于噪聲，故其參數估計相同。

表2給出了SNR=-20 dB條件下，不同分數階次步長Δp時高動態目標的參數估計情況，由表2可知，隨著步長Δp的減小，參數估計精度越來越高。

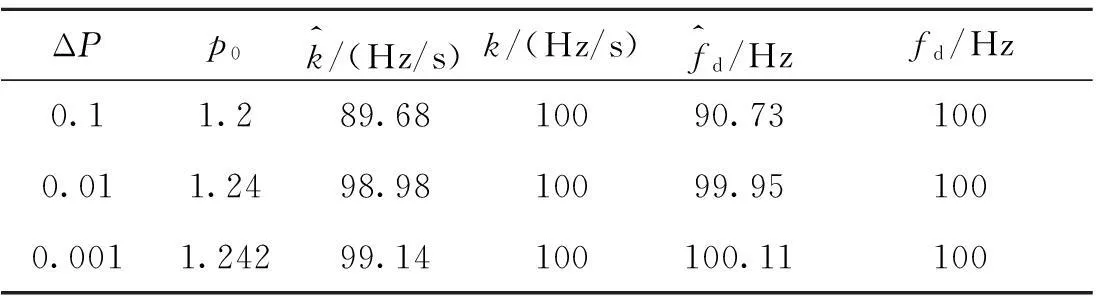
表2　不同分數階次步長ΔP時高動態目標參數估計

表3給出了-20 dB條件下，不同分段匹配濾波器個數時高動態目標的參數估計情況，由表3可知，隨著匹配濾波器個數P的增加，參數估計精度越來越高。

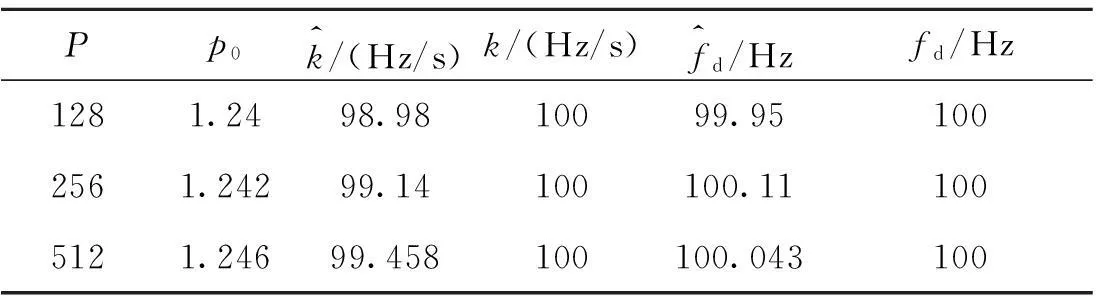
表3　不同分段匹配濾波器個數P時

4結論

在傳統捕獲算法的基礎上，本文提出了分段自相關分數階傅里葉變換的高動態目標檢測方法。該方法提出先對接收信號進行FFT變換預測多普勒頻率，然后采用PMF對信號進行降采樣，之后再進行FRFT變換，通過檢測信號峰值估算出多普勒頻移及其變化率分量。理論分析和仿真結果表明，本文提出的方法解決了傳統方法無法對頻率變化率進行補償的問題，也大大減少了FRFT算法計算量，縮短了捕獲時間。同時，所提算法利用高斯白噪聲在任意階次的分數階傅里葉域內能量分布是均勻的，在估計相關參數的同時抑制了噪聲,提高了信號的檢測信噪比，增強了系統抗噪性能，易于實現高動態環境下信號的快速捕獲，在工程實踐中具有一定的實用價值。

參考文獻:

[1]AKOPIAN D． Fast FFT based GPS satellite acquisition methods[J]．IEEE Proceedings of Radar Sonar and Navigation, 2005, 154(4):277-286.

[2]CANDIDA L S, SASCHA M S, GORDON J R P,et al. A Serial parallel FFT correlator for PN code acquisition from LEO satellites[C] // International Symposium on Spread Spectrum Techniques and Applications. Washington, DC:IEEE, 1998

[3]黃烈超,張天騏,杜曉華.基于PMF-FFT的高動態多進制擴頻信號的捕獲算法[J].計算機應用研究,2011,28(9):3407-3410.

[4]章蘭英,袁嗣杰,陳源. 航天擴頻測控系統中偽碼捕獲方法研究[J]. 電子學報，2011，06(6):1471-1476.

[5]郇浩, 陶選如, 陶然,等. 多普勒頻率變化率快速最大似然估計輔助的高動態載波跟蹤環路[J].電子與信息學報，2014，36(3):577-582.

[6]房琪. 基于分數階Fourier變換的LFM類信號的DOA估計[D].蘭州：蘭州交通大學，2013.

[7]陳斌杰,陳敏鋒.高動態下GPS信號的捕獲和跟蹤技術研究[J]. 現代電子技 術,2006,218(3):13-15.

[8]于鳳芹，曹家麟. 基于分數階傅里葉變換的多分量chirp信號的檢測與參數估計[J].電聲技術，2004:53-59.

[9]戰立曉,湯子躍,朱振波. 基于分數階傅里葉變換的加速微弱目標檢測與估計[J]. 電波科學學報,2013,28(2):296-304.

[10]Erseghe T, Kraniauskas P, Cariolaro G. Unified fractional Fourier transform and sampling theorem[J].IEEE Transactions on Signal Processing, 1999, 47(12): 3419-3423.

[11]陶然,周云松. 基于分數階傅里葉變換的寬帶LFM信號波達方向估計新算法[J]. 北京理工大學學報,2005,25(10):895-899.

High-Dynamic Target Detection Method Based on FRFT

HUANG Mingjun ，WANG Yongmin ，NIU Jiahong

(Information and Navigation College，Air Force Engineering University，Xi’an 710077，China)

Abstract:The received signal contained large Doppler frequency and its changing rate was high when the receiver in high dynamic environment, and traditional methods could not capture the changing rate of Doppler frequency for effective compensation. Aiming at this problem, a high dynamic target detection method based on fractional Fourier transform was proposed. This method first projected the receiving signals’ carrier frequency, Then using fractional Fourier transform of linear frequency modulation signal of the characteristics of energy in the optimal order times. The method of segmented autocorrelation combined discrete fractional Fourier transform to process the signal quickly and accurately. The theoretical analysis and simulation showed that this method could solve the problem that the traditional methods could not capture the changing rate of Doppler frequency for effective compensation, and improved the detection SNR and receiver’s capture probability.

Key words:high dynamic; capture; linear?frequency?modulation; fractional Fourier transform; detection

中圖分類號:TN914

文獻標志碼:A

文章編號：1008-1194(2016)01-0037-05

作者簡介:黃明軍(1990—)，男，安徽舒城人，碩士研究生，研究方向：擴頻通信、通信抗干擾。E-mail:513760454@qq.com。

基金項目:國家自然科學基金項目資助(61001111)

*收稿日期:2015-09-01