感知 感受 感悟
——《平均數》教學片斷與思考

季正偉

【教學片斷】

一、在“比”中感知平均數的意義

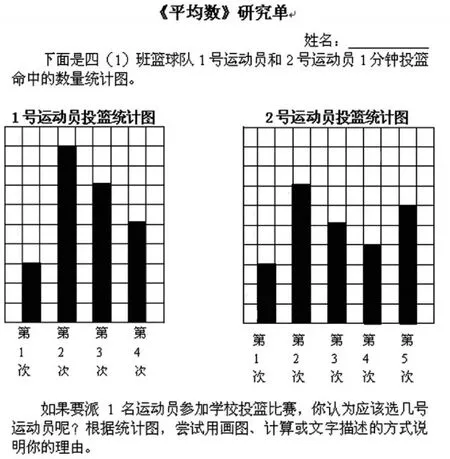
師：如果要派1名運動員參加籃球比賽，你認為應該選幾號運動員？

生：1號選手共投中24個，2號選手共投中25個，所以選2號選手。

生：1號4次投中了24個，2號5次才投中了25個，所以比較總數不合適。

師：既然大家覺得兩個人投籃的次數不同，比較總數不公平，那怎樣比才合理呢？

生：我把1號運動員第2次移3個給第1次，把第3次移1個給第4次，這樣1號運動員每次都投中了6個球；2號運動員我是把第2次移2個給第1次，把第5次移1個給第4次，這樣2號運動員每次都投中5個球。6比5大，說明1號比2號水平高。

師：大家能看懂他的意思嗎？（再找一名學生說一說）為什么要移？

生：這樣1號運動員的水平就是6個，2號運動員的水平就是5個。

師：那移之后的這個6表示什么？

生：6表示1號運動員的水平。

生：6表示1號的平均數。

師：6能表示具體哪一次的個數嗎？

生：6個不表示哪一次投中的個數，而是表示1號運動員這4次的整體的水平，也就是這4個數的平均數。就好比如這次我們單元練習班級平均分是92分，92分不代表哪一個同學的成績，而是代表我們班整體的水平。

師：那移之后的5表示什么呢？

生：5表示2號運動員5次平均每次投中5個球，代表2號運動員的整體水平。

師：數學上把這樣的方法叫做“移多補少”，通過“移多補少”我們能找出一個數表示一組數據的整體水平，這個數就叫做“平均數。”還有其他方法比較嗎？

生：我是計算的，先算出1號運動員一共投中24個球，再除以一共投了4次，算出他平均每次投中6個；2號運動員也是一樣，先算出一共投中25個球，再除以5次，算出平均每次投中5個，6比5大，所以應該派1號運動員去。

師：這樣的方法數學上叫做“求和平分”，雖然兩個同學介紹的方法不一樣，但是存在什么聯系呢？

生：都是變成一樣多了。

生：移多補少是把多的拉下來給少的，使每次一樣多。求和平分是先算出總數再平均分，也是使每次一樣多。我覺得這是它們一樣的地方。

師：不管是哪種方法，目的是讓每個數都一樣，這里的6就是 3、9、7、5 的平均數，而 5則是 3、7、5、4、6 的平均數，它們代表了兩個人投藍的整體水平。回憶一下，咱們解決誰的水平高這個問題的過程，其實就是我們認識平均數的過程，想想你對平均數有了什么認識？

生：平均數不代表哪一次的水平，而是代表運動員的整體水平。

生：可以用“移多補少”和“求和平分”這兩種方法求平均數。

【教學思考：這節課，我用“選幾號運動員參加比賽”作為引領學生獨立思考、小組討論、展示分享的主線，讓學生通過解決這樣一個與生活結合密切的問題來感知平均數的產生、意義以及作用。誰的水平高中的“水平”其實就是平均數的代名詞，這一個簡潔而易懂的問題，既貼近學生的生活，又調動了學生已有的知識儲備和生活經驗 。“移多補少”、“求和平分”等形象化的呈現方式是促進理解的最佳途徑，在移多補少的基礎上，讓學生展示求和平分的方法，從而體會求平均數一般有兩種方法。】

二、在“選”中感受平均數的方法

【教學片斷】

師：平均每個筆筒里有多少支鉛筆？

生：6支。

師：反應這么快，怎么知道的？

生：移多補少。

師：這一次平均每個筆筒里有多少支鉛筆？

師：為什么反應沒剛才快了？這時用什么方法求平均數更合適？

生：求和平分。

師：通過這兩個練習，你對平均數又有了哪些新的認識？

生：數據少且接近時用“移多補少”更快一些，數據多且數據相差較大時用“求和平分”更合適一些。

【教學思考：通過兩個練習的對比，使學生感受到面對不同的平均數問題應靈活選擇不同的方法解決，當面對數量較多且懸殊較大的數據時，選用求和平分的計算方法更合理。】

三、在“變”中感悟平均數的特征

【教學片斷】

師：大家覺得這次應該選擇什么方法求平均身高？

生：求和平分。

師：估一估，你覺得平均數可能是多少？

生：160厘米。

生：161厘米。

生：159厘米。

師：會不會是170厘米呢？

生：不可能，平均數要移多補少，最高的是165厘米，他還要移些給矮的同學，平均身高只會比165矮。

師：那肯定比誰高呢？

生：比154厘米高，因為高的同學還要移些給他，肯定要比154厘米多。

師：看來平均數是有一個范圍的。

生：平均數比最小的數大，比最大的數小。

生：我還知道平均數一般接近最大數和最小數中間的一個數。

師：具體是多少呢？算一算。（計算出平均身高是160厘米）

師：通過剛才的練習，你對平均數又有了哪些新的認識？

生：平均數是有范圍的，它比最小的數大，比最大的數小。

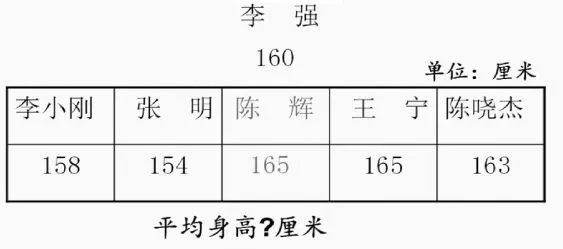
師：一天，由于李強請假了，教練將身高160厘米的李強換成了165厘米的陳輝，現在籃球隊的平均身高和原來比有什么變化？

生：我是這樣認為的，原來平均身高是160厘米，李強身高也是160厘米，他不要移別人的，也不要移給別人，現在陳輝身高是165厘米，他還可以給別人一些，所以平均身高會增加。

生：原來李強160厘米換成陳輝165厘米，他們的身高總和就多了5厘米，但是人數沒變，我們可以把這多的5厘米分給5個人，每人會多出1厘米，所以我可以知道現在籃球隊五人的平均身高是161厘米。

師：如果換成170厘米的運動員呢，平均身高會多多少？那換成155厘米的運動員呢？

師：通過剛才的練習，你對平均數又有什么新的認識？

生：一組數據中只要有一個數據變化了，平均數就會發生變化。

師：難怪有人這樣形容平均數：“平均數很敏感，任何一個數的風吹草動，都會使平均數發生變化。”現在看來這話有道理嗎？所以平均數是具有“不穩定”性的。

【教學思考：在計算平均身高前讓學生進行估算，學生根據經驗能感覺出大概的平均身高，在學生的不斷補充中悟出了平均數的范圍，平均數都比最小的數大，比最大的數小。】