《認識負數》教學實踐與思考

牛獻禮（特級教師）

【教學內容】

人教版六年級下冊第2、3頁。

【教學過程】

一、激活經驗，多元表征

師：今天我們學習“負數”（板書課題），聽說過負數嗎？會不會寫？請在本子上任意寫出一個負數。

（教師選擇部分學生的作品展示：-1、-2、-5、-100）

師：誰會讀？

生：減 1、減 2……

生：不對，應該讀負1、負2……

師：這個讀法是對的！負數里面的這個符號跟“減號”長的一樣，但不讀成“減”，它是“負號”，應該讀成“負”。我們一起來讀一讀。

生：負一、負二、負五、負一百。

師：想一想，你在哪里見到過這些負數？能舉個例子說說它的含義嗎？

生：坐電梯的時候，地下一層用-1表示。

生：天氣預報，零下5度用-5度表示。

生：賣東西，賠了100元，用-100表示。

……

師：看來，負數在生活中的應用真的很廣泛！那么負數表示什么意義呢？我們就以-2做例子，請你用自己喜歡的方式表示出它的意義，畫圖、列算式、寫文字都可以。

（學生獨立思考，自主嘗試，然后全班交流，集體反饋）

生：1-3=-2。

生（畫了一個電梯圖）：地下二層是-2。

生（畫了一個溫度計）：零下2度是-2。

生：賣東西，虧了2元是-2。

……

【思考：負數在日常生活中很常見，因此，學生對負數的讀、寫有一定的經驗基礎，只不過會有部分學生把負號讀成“減”，對負數意義的理解還不夠清晰，對相反意義的量的表示也僅有一些朦朧意識。通過讓學生描述生活中見到的負數，激活了學生頭腦中“沉睡”的關于負數的經驗。接著，給學生提供自主探索的空間，引導學生用自己的方式表示心目中的“-2”，這樣就將學生的認知過程外顯化，便于教師據此施教，也為后續學習提供了素材。由于學生的經驗和知識基礎的差異，他們對于“-2”的表征方式必定也是多元的，一般為“小數減大數的算式”、“溫度計上的零下溫度”、“電梯示意圖中的地下二層”等等。分析、解釋這些表征的過程，就是認識負數并加深理解的過程，有益于學生思維品質的提升。】

二、理解意義，建立概念

1.溫度計上的正負數。

師：我們就以溫度計為例子來研究一下。為了看得更清楚，我們把溫度計放大。

師：觀察一下溫度計上有兩個2℃，如何區分？

生：一個是零上2℃，一個是零下2℃。

師：生活中經常用“零上”和“零下”來區分溫度，還有別的區分方法嗎？

生：0上2格的是2℃,0下2格的是-2℃。

師：0在這里有什么作用？

生：0有分界的作用，高于0℃是零上溫度，低于0℃是零下溫度。

師：現在明白為什么用-2℃表示零下2℃了吧？

生：為了跟零上2℃區分開。

師：因為有兩個2℃，是零下還是零上要區分開來。以前學過的數只能夠表示零上溫度或零度，那零下溫度就要用負數來表示了。

（板書：零下2℃用-2℃表示，零上2℃用2℃表示）

（讓學生讀一讀，再次逐一出示學生對“-2”的表征，讓學生完整表述它的含義）

（板書：地上2層記作2層，地下2層記作-2層；賺2元記作2元，虧2元記作-2元）

【思考：通過讓學生觀察溫度計上零上2度和零下2度寫著的都是2度，使學生明白“為什么要用-2度來表示零下2度”，體會負數產生的必要性。接著，通過“零上2度記作2度，零下2度記作-2度；地上2層記作2層，地下2層記作-2層……”等幾組相反意義的量的比較，使學生體會負數不會單一表示，而是會與正數一起形成一組相反意義的量，初步體會到正負數的規定性。】

2.理解相反意義的量。

師：觀察上面用2和-2表示出來的這些信息，它們有什么共同特點？

生：每一組的意思都是相反的，比如“地上2層與地下2層”、“賺和虧”。

生：就好像語文當中的反義詞一樣。

師：零上和零下、地上和地下……每組的意義都相反，這使我們明白了一個道理：2和-2表示一組相反意義的量。（板書：相反意義的量）

師：除了2和-2，還能舉出其他例子來表示另外一些相反意義的量嗎？

生：往左走10米記作10米，往右走10米記作-10米。

（板書：左、右 10、-10）

生：順時針轉6圈記作6圈，逆時針轉6圈記作-6圈。

（板書：順、逆 6、-6）

……

師：這些負數的表示都十分符合人們的生活習慣。下面的數能理解嗎？

［出示：存折上的支出、收入數據（課本第3頁）］

生：2000表示存入 2000元，-500表示支出500元。

生：-132表示支出 132元，500表示存入500元。

師：存入和支出也是一組表示相反意義的量。存入為正，支出為負。

師：像以前學過的很多數都是正數。+500，讀作正五百，2000也可以寫成+2000，讀作正二千，省去正號和加上正號都是正數。正號可以省略，那負號可以省略嗎？為什么？

生：去掉負號就變成正數了，就不能區分相反意義的量了。

師：回想一下，以前學習中，當測量結果無法用整數表示的時候，我們就去認識了分數和小數。人們在生活中經常會遇到各種相反意義的量。比如,在記錄溫度時有零上有零下；在計算生活收入開支時，有時要記收入多少，有時要記支出多少。為了方便，人們就考慮用正負數來表示兩種相反意義的量。

【思考：通過讓學生舉例、解釋等方式對相反意義的量的理解進行拓展、歸納，進一步理解正負數表示“相反意義的量”。接著，通過能否省去數前面的“+”和“-”的討論以及聯系前面學過的分數、小數的產生過程，再一次加深對負數產生必要性的理解。】

三、應用練習，深化理解

1.（1）樂樂長大了，今年的體重比去年增加了3.5千克記作（+3.5）千克；媽媽減肥成功，體重比上月減輕了3.5千克記作（ ）千克。

（2）向東走10米記作（ ）米，那么向西走14米記作（）米。

生：體重增加3.5千克記作+3.5千克，體重減輕3.5千克，記作-3.5千克。

生：向東走10米記作+10米，那么向西走14米記作-14米。

生：還可以這樣，向東走10米記作-10米，那么向西走14米記作+14米。

師：可以這樣嗎？有兩種答案？

生：兩種都對。因為規定了正數，與它相反的可以用負數來表示。

師：只要規定合理，兩種都是可以的。看來規定哪個為正數是非常重要的。

2.小華身高可以表示為-2厘米。

師：你覺得可能嗎？

生：不可能，因為人的身高不可能是負數的。

生：有可能，如果找一個比小華高2厘米的人為標準，那么小華身高可表示為-2厘米。

師：據統計，全國12周歲兒童身高的正常范圍為140～160厘米。

生：小華158厘米，如果以160厘米為標準，記作0，小華可表示為-2厘米。

師：如果以最低的140厘米為標準呢？

生：小華可表示為+18厘米。

師：同樣一個小華，怎么一會兒用正數表示，一會兒用負數表示，你又有什么想法？

生：以誰為“0”非常重要！

師：好一個變化多端的“0”！看來確定標準是關鍵。標準變化，就會引起正、負的變化。

3.北京連續5天的最低氣溫統計表。

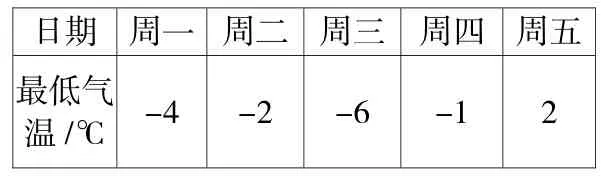
日期　周一　周二　周三　周四　周五最低氣溫/℃　-4　-2　-6　-1　2

師：溫度計把水結冰的溫度規定為0度，以0為界，0上為正，0下為負（課件動態演示：溫度計橫過來，逐步抽象成直線）請把表中這些數表示在這樣的直線上。

（展示學生代表性作品）

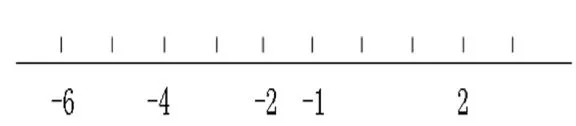
第一種：

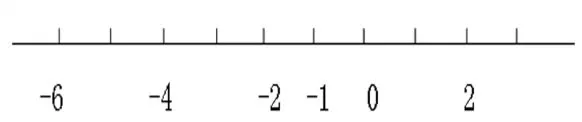
第二種：

師：你更喜歡哪一種寫法？為什么？

生：我喜歡第二個，因為第一個沒有寫0，不是很清楚。

師：為什么寫了0就清楚了呢？

生：因為0是正負數的分界點，有了分界點就清楚了。

（課件演示：先在直線上寫0）

師：2寫哪里呢？

生：往0的右邊數2格。

師：為什么是往右邊數2格？

生：因為越往右越大。

師：為了研究方便，數學上通常把0的右邊規定為正，用箭頭做個記號（課件演示：添加表示正方向的箭頭），這樣帶有正方向的直線叫做數軸。

（板書：數軸）

師：-2在哪里呢？

生：從0往左數2格就是-2。

師：-4呢？

生：從0往左數4格就是-4。

師：這是-4，那表示相反意義的+4該在哪里呢？

生：在0的右邊數4格。

師：剛才我們學習的一直都是正整數、負整數，能在數軸上表示正負分數、正負小數嗎？+1.5在哪里？

生：從0往右數1格半的位置。（課件顯示：在數軸上標出+1.5）

師：那表示和它相反意義的-1.5在哪兒呢？

生：從0往左數1格半的位置。（課件顯示：在數軸上標出-1.5）

師：仔細觀察這個數軸上的正負數，你有什么發現？

生：我感覺這樣一對一對的正、負數，都是對稱的。

師：（課件一對一對演示）確實是對稱的。這樣一對數中，總是一個為正，另一個就為負。有個數卻很孤單。

生：0

師：這說明什么？

生：0既不是正數，也不是負數。

師：還有別的發現嗎？

生：我發現每一對正負數離0的距離都是相等的，而且正負號后面的數越大，這個數離0就越遠。

師：剛才有同學寫出了1-3=-2，現在你能借助這個數軸來解釋一下它為什么等于-2嗎？

生：減去3就要往左數3格，從1開始往左數3格正好是-2，所以得數是-2。

師：講得真好！這是我們以后初中要繼續學習的內容。

【思考：通過把溫度計橫放、抽象成直線，引導學生脫離具體的情境，把數軸的點和抽象的正負數對應起來，直觀體會數軸上正負數的排列規律。接著，引導學生根據知識的遷移類推，探討如何在數軸上表示分數和小數，以完善學生對數概念的建構。最后根據數軸來解釋1-3=-2的意義，把課延續到了初中數學。】