《導(dǎo)數(shù)及其應(yīng)用》單元教學(xué)設(shè)計

安常勝

【摘要】教師在設(shè)計教學(xué)時，應(yīng)有一個整體計劃，要根據(jù)模塊章節(jié)、關(guān)聯(lián)知識、數(shù)學(xué)方法來設(shè)計教學(xué)，而不能局限在某個知識點來設(shè)計。數(shù)學(xué)課程設(shè)計要突出主線，這對于學(xué)生理解數(shù)學(xué)將是非常重要的，也有助于學(xué)生提高應(yīng)用能力。本文以《導(dǎo)數(shù)及其應(yīng)用》為例，從不同方面介紹如何總體把握課程。

【關(guān)鍵詞】單元教學(xué)設(shè)計

【中圖分類號】G633.6 【文獻標(biāo)識碼】A 【文章編號】2095-3089（2016）02-0182-02

“單元教學(xué)設(shè)計”就是根據(jù)整套教材的結(jié)構(gòu)體系和課程標(biāo)準(zhǔn)的要求，從模塊章節(jié)、關(guān)聯(lián)知識、數(shù)學(xué)方法等角度出發(fā)，按照數(shù)學(xué)分析、課標(biāo)分析、學(xué)生分析、教材分析、重難點分析、教學(xué)安排等方面，對相關(guān)內(nèi)容或方法優(yōu)化整合，形成完整、總體的教學(xué)設(shè)計。“單元教學(xué)設(shè)計”體現(xiàn)整體性、相關(guān)性、階梯性、綜合性的基本要求。實現(xiàn)教師整體把握高中數(shù)學(xué)課程，不斷開拓視野和提高教學(xué)能力。例如，高中數(shù)學(xué)教材中所涉及到的垂直關(guān)系、函數(shù)單調(diào)性、常用邏輯用語等，都可作為一個“單元”，教師從不同角度和層次進行教學(xué)設(shè)計。這種系統(tǒng)教學(xué)設(shè)計的方法，既幫助了教師整體把握章和單元的教學(xué)內(nèi)容與教學(xué)形式，也更方便學(xué)習(xí)者理清知識點之間的關(guān)系，形成體系更加完整、結(jié)構(gòu)更加堅固的知識結(jié)構(gòu)。根據(jù)單元教學(xué)設(shè)計的理念，結(jié)合教學(xué)實際，對人教版選修2-2《導(dǎo)數(shù)及其應(yīng)用》本章為單元，淺談如何整體把握和實施教學(xué)過程。

一、單元教學(xué)目標(biāo)

1.了解微積分概念的實際背景和幾何意義，能夠利用微積分解決簡單與函數(shù)性質(zhì)有關(guān)的問題和某些實際問題。

2.通過豐富的實際背景創(chuàng)設(shè)情境，教學(xué)中重現(xiàn)新概念的背景、產(chǎn)生、發(fā)展、完善的過程，呈現(xiàn)數(shù)學(xué)的本來面目。通過學(xué)習(xí)微積分，體會從局部到整體，再由整體到局部的思想方法，學(xué)會以動態(tài)的、變化的、無限的變量數(shù)學(xué)觀點來研究問題，而不僅僅是停留在靜態(tài)的、不變的、有限的常量數(shù)學(xué)觀點上。

3.通過數(shù)學(xué)文化的學(xué)習(xí)，可以使學(xué)生了解數(shù)學(xué)科學(xué)與人類社會發(fā)展之間的相互作用，體會數(shù)學(xué)的科學(xué)價值、應(yīng)用價值和人文價值，并從中受到優(yōu)秀文化的熏陶，領(lǐng)會數(shù)學(xué)的美學(xué)價值，從而提高自身的文化素養(yǎng)和創(chuàng)新意識。

二、要素分析

1.數(shù)學(xué)分析

《導(dǎo)數(shù)及其應(yīng)用》在整個高中數(shù)學(xué)教材中占有非常重要的地位和作用。它既是對函數(shù)知識的補充和完善，也為今后進一步學(xué)習(xí)微積分奠定基礎(chǔ)。

2.標(biāo)準(zhǔn)分析

《導(dǎo)數(shù)及其應(yīng)用》內(nèi)容要求注重對導(dǎo)數(shù)本質(zhì)的認(rèn)識（要求把導(dǎo)數(shù)作為一種重要的數(shù)學(xué)思想、方法來學(xué)習(xí)），提高對導(dǎo)數(shù)應(yīng)用性的要求，降低了對求導(dǎo)計算和定積分計算的要求。

3.學(xué)生分析

（1）學(xué)習(xí)水平分析：學(xué)生學(xué)習(xí)水平和能力比較好。

（2）知識儲備分析：學(xué)生已經(jīng)學(xué)習(xí)函數(shù)的相關(guān)性質(zhì)，而且能夠利用性質(zhì)解決一些函數(shù)綜合性問題，但學(xué)生沒有學(xué)習(xí)數(shù)列的極限、函數(shù)的極限、函數(shù)的連續(xù)性等知識的基礎(chǔ)上具體、直觀的認(rèn)識微積分的數(shù)學(xué)思想。

4.重難點分析

教學(xué)重點：導(dǎo)數(shù)概念的建立及其幾何意義；簡單函數(shù)的導(dǎo)數(shù)運算；利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性，極值、最值等性質(zhì)。

教學(xué)難點：在沒有極限的條件下建立導(dǎo)數(shù)的概念；體會極限意義下的數(shù)學(xué)與精確意義下的數(shù)學(xué)的區(qū)別和聯(lián)系；利用導(dǎo)數(shù)研究函數(shù)的性質(zhì)；微積分基本定理。

5.考點分析

函數(shù)與導(dǎo)數(shù)應(yīng)用客觀題主要考察導(dǎo)數(shù)的計算；導(dǎo)數(shù)的幾何意義；單調(diào)區(qū)間、極值、最值的求解；分段函數(shù)、函數(shù)定義域、函數(shù)性質(zhì)、函數(shù)圖像與變換、函數(shù)零點；已知函數(shù)的單調(diào)性、最值、極值等求參數(shù)的取值范圍以及與不等式的綜合應(yīng)用；定積分的運算；利用定積分求平面圖形的面積。函數(shù)與導(dǎo)數(shù)解答題，主要考查單調(diào)性、極值點、導(dǎo)數(shù)公式與運算、函數(shù)方程的思想，靈活運用導(dǎo)數(shù)分析問題、解決問題的能力。以導(dǎo)數(shù)的綜合應(yīng)用為主，函數(shù)、方程、不等式、曲線切線等綜合命題。

6.教學(xué)方式分析

應(yīng)用現(xiàn)代教育技術(shù)，通過實例分析法、探究式教學(xué)法、直觀教學(xué)法進行教學(xué)設(shè)計。

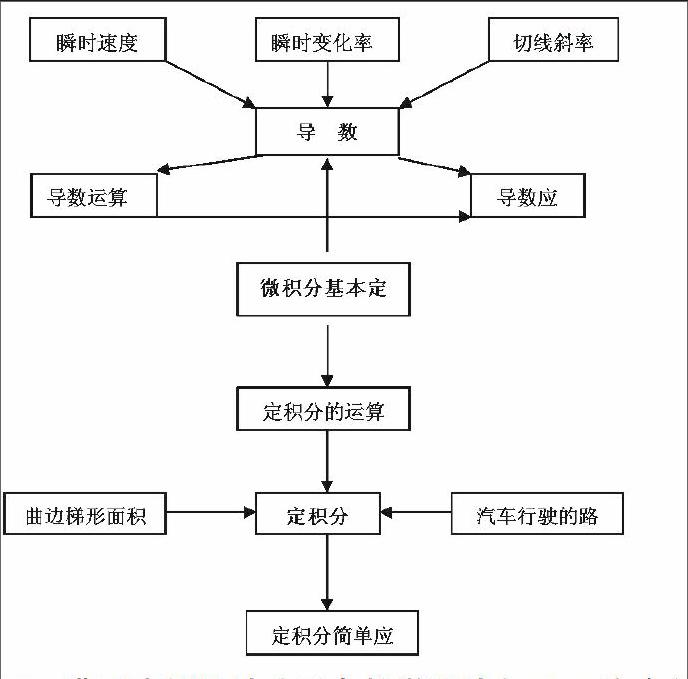
三、教學(xué)流程設(shè)計

四、典型案例設(shè)計（重點教學(xué)設(shè)計）1.5.2汽車行駛的路程

創(chuàng)設(shè)情境

問題1：汽車以速度v作勻速直線運動時，經(jīng)過時間t所行駛的路程為S=vt.如果汽車作勻速直線運動，在時刻t的速度為v（t）=0.6（單位：km/h），那么它在0≤t≤1（單位：h）這段時間內(nèi)行駛的路程s（單位：km）是多少？

學(xué)生活動：通過確定汽車以速度v作勻速直線運動的路程，利用速度--時間函數(shù)圖像發(fā)現(xiàn)路程的幾何意義，其幾何意義就是： t=0， t=1，v=0，v=0.6所圍成的圖形面積。

問題2：如果汽車作變速直線運動，在時刻t的速度v（t）=0.6 t（單位：km/h），那么它在0≤t≤1（單位：h）這段時間內(nèi)行駛的路程s（單位：km）是多少？

學(xué)生活動：根據(jù)物理知識，確定汽車在這段時間內(nèi)行駛的路程，結(jié)合速度—時間函數(shù)圖像發(fā)現(xiàn)由t=0， t=1，v=0，v= 0.6 t所圍成的圖形面積在數(shù)值上與汽車行駛路程的關(guān)系，進一步明確路程的幾何意義是對應(yīng)圖形的面積。

分析：通過探究1、2發(fā)現(xiàn)路程的幾何意義，為探究3汽車作變速運動時，其路程的確定問題化歸到曲邊梯形面積的方法上。

新課探究

問題3：如果汽車作變速直線運動，在時刻t的速度為（單位：km/h），那么它在0≤t≤1（單位：h）這段時間內(nèi)行駛的路程S（單位：km）是多少？

分析：利用問題1、2得到路程s的幾何意義，汽車行駛的路程在數(shù)據(jù)上等于由直線和曲線所圍成的曲邊梯形的面積.所以與求曲邊梯形面積類似，采取“以不變代變”的方法，把求勻變速直線運動的路程問題，化歸為勻速直線運動的路程問題.把區(qū)間分成n個小區(qū)間，在每個小區(qū)間上，由于的變化很小，可以近似的看作汽車作于速直線運動，從而求得汽車在每個小區(qū)間上行駛路程的近似值，在求和得S（單位：km）的近似值，最后讓n趨緊于無窮大就得到S（單位：km）的精確值.（思想：用化歸為各個小區(qū)間上勻速直線運動路程和無限逼近的思想方法求出勻變速直線運動的路程）。

五、反思與改進

1. 理解課程標(biāo)準(zhǔn)的要求，把握課堂教學(xué)主線——逼近思想、以直代曲思想、數(shù)形結(jié)合思想。

2. 寓德教學(xué)于數(shù)學(xué)教學(xué)之中。激發(fā)學(xué)生的學(xué)習(xí)興趣，培養(yǎng)民族責(zé)任感，激發(fā)學(xué)生的熱情，樹立為振興中華，開創(chuàng)未來的崇高理想和為科學(xué)獻身的遠(yuǎn)大志向。

3. 在教學(xué)中傳授給學(xué)生知識的過程中，應(yīng)培養(yǎng)學(xué)生自主學(xué)習(xí)的能力和思維品質(zhì)。

參考文獻：

[1]曹莉莉.《新課程理念下課堂教學(xué)評價的標(biāo)準(zhǔn)》[J].教育科學(xué)研究，2003.7：8—12.

[2]高慎英.《“有效教學(xué)”的理想》[J].課程·教材·教法，2005.8：12-19.

[3]何克抗.現(xiàn)代教育技術(shù)培訓(xùn)教程[M].北京：高等教育出版社， 2005：10-13.

[4]季蘋.《如何落實三維目標(biāo)？（二）——對“單元教學(xué)設(shè)計”的探討》[J].基礎(chǔ)教育課程，2005.09

[5]管錫基.《“和諧高效思維對話”型課堂教學(xué)研究綜述》[J].當(dāng)代教育科學(xué)，2010年第12期.

[6]夏清.《單元教學(xué)設(shè)計背景下的課堂有效教學(xué)》[J].科學(xué)教育，2010年第6期.

本文為甘肅省教育科學(xué)規(guī)劃“十二五”立項課題（GS[2014]GHB1076）的階段性成果。