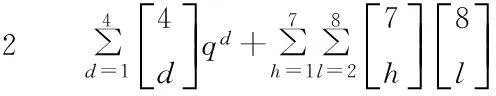確定多指標醫學參考值范圍的統計方法

?

確定多指標醫學參考值范圍的統計方法

陳彬1， 紀超娜2

(1.四川大學華西公共衛生學院， 四川 成都 610041； 2. 汕頭大學醫學院附屬第一醫院， 廣東 汕頭 515041)

【關鍵詞】三類指標組合指標法； 參考值范圍； 參考值； 多指標醫學參考值范圍

第十三講三類指標組合指標法

三類指標組合指標法(method of combinatorial indicatrixes for three categories indicatrixes， 陳 彬等，2005)是將所觀察的m項指標按醫學意義分為三大類，當每類中至少有1項指標異常時判斷受試者的某功能或某器官狀態為異常，若指標異常個數少時，或異常類數少時則判為可疑異常。

1基本公式

1.1多指標百分位數法(精確法)

計算各指標的參考值范圍的百分數Pi(i= 1，2，……，m；m為指標個數)，設各指標的參考值范圍的百分數Pi相等，均為p，，則：

(1)

p=1-q。

(2)

一般用迭代法求q，q的初始值q0用下式求解。

q0=1-P1/m。

(3)

…式中P為參考值總百分數，m為指標個數，一般k≦ 5，當k過大時，qk很小而無實際意義。

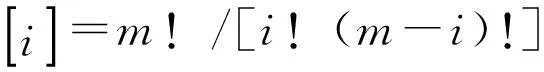
(4)

1.2組合指標法計算各指標的參考值范圍的百分數Pi(i= 1，2，……，m；m為指標個數)，設各指標的參考值范圍的百分數Pi相等，均為p，則：

(5)

p=1-q

(6)

一般用迭代法求q，q的初始值q0用下式求解。

q0=1-P1/m。

(7)

…式中P為參考值范圍總百分數，m為指標個數，一般k≦5，當k過大時，qk很小而無實際意義。

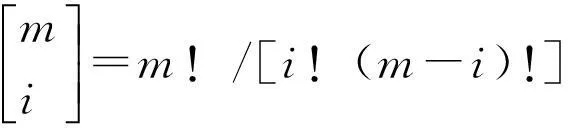
(8)

1.3兩類指標組合指標法

(9)

式中，m表示指標個數，m1、m2分別第1、2類指標個數，P表示總參考值范圍的百分數，q的是異常率(陽性率)。一般用迭代法求q，q的初始值q0用下式求解。

(1)

k1=a+5≤m1,

(11)

k2=b+5≤m2,

(12)

當迭代n次后終止，可用下式求兩類指標參考值范圍的百分數：

第1類指標p1=1-qn;

(13)

第2類指標p2=1-λqn。

(14)

式中qn為迭代n次后求得的第1類指標異常百分數，λqn為迭代n次后求得的第2類指標異常百分數。兩類陽性率的比值為q1∶q2=1∶λ。

1.4三類指標組合指標法

(15)

k1=a+5≤m1,

(16)

k2=b+5≤m2,

(17)

k3=v+5≤m3,

(18)

式中，m表示指標個數，m1、m2、m3分別為第1、2、3類指標個數，P表示總參考值范圍的百分數，q的是異常率(陽性率)。一般用迭代法求q，q的初始值q0用下式求解。

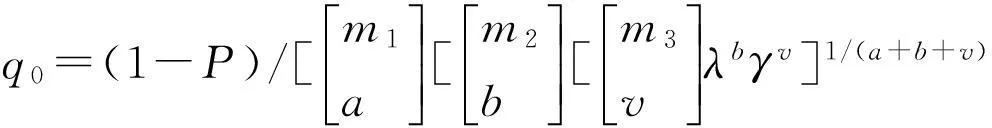
(19)

當迭代n次后終止，可用下式求三類指標參考值范圍的百分數：

第1類p1=1-qn;

(20)

第2類p2=1-λqn;

(21)

第3類p3=1-γqn。

(22)

三類指標陽性率的比值為

q1∶q2∶q3==1∶λ∶γ。

(23)

2分析步驟

(1)確定a、b、v值觀察受試者的m項指標，按醫學意義分為三大類，第1類有m1項指標，第1類有m2項指標，第3類有m3項指標，第1類中至少有a(1≤a≤m1)項指標異常，同時第2類中至少有b(1≤b≤m2)項指標異常，同時第3類中至少有v(1≤v≤m2)項指標異常，則判斷受試者的某功能或某器官狀態為異常，而出現異常指標少時，或出現異常類數少時，通常判斷受試者的某功能或某器官狀態為可疑異常。a、b、v值通常由該領域的醫學專家論證、確定。

(2)確定λ、γ值 三類指標陽性率比值為

q1∶q2∶q3=1∶λ∶γ。當三類指標陽性率相等時λ=γ=1 。

(3)確定各指標的參考值范圍的百分數兩種可能：(1)獨立應用三類組合指標法基本公式；一般用迭代法求q，當q前后兩次迭代結果的差值小于指定值時終止迭代。(2)根據醫學情況，幾個基本公式組合、構建方程。如部分指標可分為三大類，在其余項指標中，存在只要有單獨1項指標異常就有診斷意義！或至少有2項指標異常時，或兩種情況同時存在，等，均能判斷受試者的某功能或某器官狀態為異常。

(4)確定每項指標的單、雙側及其相應的參考界值的百分數

單側： 下限PL=1-p；

(24)

上限PU=p。

(25)

雙側： 下限PL=(1-p)/2,

(26)

上限PU=p+(1-p)/2 。

(27 )

(5)確定各指標參考界值根據PL、PU，按未分組資料單指標百分位數新法，或資料近似服從正態分布時用單指標正態分布法(參看多指標正態分布法) 確定各指標參考界值。

(6)建立可疑參考值范圍？出現異常指標個數少時，或出現異常類數少時，通常判斷受試者的某功能或某器官狀態為可疑異常。

(7)醫學實踐檢驗與調整參考界值。

(8)臨床診斷試驗評價。

3應用實例

某醫師觀察101例健康成人某功能狀態,資料見表11-1 。為判斷某功能狀態是否正常，請用三類指標組合指標法確定95 % 多指標臨床醫學參考值范圍(單側、下限)？

表11-1觀察101例健康成人某功能狀態及95 % 多指標臨床醫學參考值范圍

指標1號50號95%多指標臨床醫學參考值范圍1類X111.91.7>2.0X125.34.3>4.8X1323.622.8>22.62類X2165.864.9>64.7X2292.591.3>92.03類X31124.5124.9>123.6X32198.1194.3>196.3

注：各指標小于參考界值為異常。在三類中，當每一類均有1項指標異常時，判斷受試者的某功能狀態為異常；當異常指標數少，或異常類別少時，判斷受試者的某功能狀態為可疑異常。

分析如下：

(1)確定a=1，b=1，v=1 ；m1=3，m2=2，m3=2。在三類中，當每一類均有1項指標異常時，判斷受試者的某功能狀態為異常；當異常指標數少，或異常類別少時，判斷受試者的某功能狀態為可疑異常。

(2)確定q1∶q2∶q3==1∶λ∶γ=1∶1∶1。即三類指標陽性率相同。

(3) 確定各指標的參考值范圍的百分數本例,P=0.95, 1-P=0.05,m=7, 設誤差ε=0.0001, 則按題意構建方程如下：

一般用迭代法求q，q的初始值q0用下式求解。

將q0=0.1609 代入方程，則

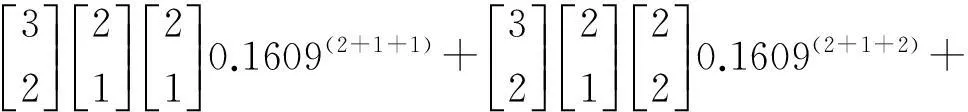
0.068 245-0.05 =0.018 245>0.0001, 取q1

(4) 確定各指標參考界值 根據P=0.8536，按未分組資料單指標百分位數新法，確定各指標單側下限參考界值，結果見表11-1。按未分組資料單指標百分位數新法，對第1個指標確定單側下限參考界值如下：

P14.64=X14.64 %(101-1)=1.9+(2.0-1.9)(6.4)/10=1.964≈2.0 。

如：第1類資料如下：

秩次012345…1112131415…觀察值X110.20.30.40.60.70.8…1.41.61.71.92.0…

其他指標的下限值見表11-1。

(5) 醫學實踐檢驗 以50號受試者為例，其X11、X12、X22、X32均小于參考界值，在4項異常指標中，1類有2項，2、3類中各有1項，故可認為此受試者具有某狀態危險因素(假陽性)。

4評論

三類指標組合指標法是綜合了許多確定多指標醫學參考值范圍的統計方法。在三類指標組合指標法基本公式中，含組合指標法、多指標百分位數法(精確法)、兩類指標組合指標法的基本公式。

三類指標組合指標法的應用條件中，注意的是全部或部分指標分為三類，關于三類指標如何判定，a、b、v如何確定，一般說均應由醫學專家確定。

(本講座終)

【參考文獻】

[1] 陳彬，李麗萍，張慶英，等. 未分組資料百分位數新計算方法 [J]. 西部醫學，2005， 17(1)：87-89.

[2] 陳彬， 張慶英，李麗萍，等. 確定多元醫學參考值的三類指標組合指標法 [J]. 西部醫學， 2005， 17 (2)： 32 - 34.

第十三講思考題(答案見：西部醫學，2015，27(1)：160.)

1 為什么講組合指標法、兩類指標組合指標法、多指標百分位數法(精確法)是三類指標組合法的特例？

2 三類指標組合法的特征？

第十二講思考題答案

1 單、雙側均可，必須有2個或兩個以上的回歸方程，方程可以是曲線或直線、多重線性回歸；應用條件既滿足回歸分析要求，同時考慮滿足結合的相應的其他確定多指標醫學參考值范圍的統計方法應用條件。

2 當確定各應變量指標的參考值范圍百分位數時，若使用的方法是近似法則稱多個回歸方程法(近似法)，若使用的方法是精確法則稱多個回歸法(精確法)

第十一講思考題答案

1 全部或部分指標分為兩類，指標彼此獨立，不拘分布，單雙側均可，樣本例數較大，類間有判斷效能差異，類內有相同效能； 兩類均有異常時有意義，且任一類出現異常時亦有意義；類間指標陽性率可相同亦可不同，但類內指標陽性率必須相同，能確定a、b值。

【中圖分類號】R 195.1； R 311

【文獻標志碼】C

doi：10.3969/j.issn.1672-3511.2016.01.039