基于粒子群隱式空間映射算法設計的雙頻濾波器

張友俊，王連棟

（上海海事大學 信息工程學院，上海 201306）

基于粒子群隱式空間映射算法設計的雙頻濾波器

張友俊，王連棟

（上海海事大學 信息工程學院，上海 201306）

將粒子群算法（Particle Swarm Optimization，PSO）用在隱式空間映射（Implicit Space Mapping，ISM）的參數提取中，可以有效改善參數提取過程中算法的不收斂性。首次在參數提取中引入PSO，主要的研究內容是改進了ISM算法。通過改進ISM算法中粗糙模型（Coarse Model, CM）與精細模型（Fine Model, FM）之間的參數映射，可以明顯減少迭代次數。以一個雙模濾波器為例，利用粒子群 ISM 算法設計了一個可以工作在無線局域網（WLAN）頻段的微帶雙頻帶濾波器，中心頻率分別是2.45 GHz和5.25 GHz。濾波器經過3次迭代并進行微調后達到了設計指標。由此可見，引入PSO之后顯著地減少了在FM中的仿真次數，有效地提高了濾波器的設計效率。

粒子群算法；隱式空間映射算法；參數提取；粗糙模型；精細模型；雙頻帶濾波器

空間映射算法利用了精細模型（Fine Model, FM）的準確性和粗糙模型（Coarse Model, CM）的快速性的特點，建立兩者之間的映射，把費時的優化過程放在CM中進行，FM只進行驗證工作。該思想最早是由Bandler于1994年提出的，后來逐漸發展出現了漸進空間映射（Aggressive Space Mapping）、ISM和神經網絡空間映射（Neural Space Mapping）等多個門類[1-5]。

在這些空間映射算法中，ISM 算法屬于實現最為簡單的方法。在濾波器的設計中存在著一些預先設定的參數，比如基板的相對介電常數和厚度，這些參數的變化會對濾波器的性能產生顯著影響。ISM算法在第代過程中通過使CM的響應逼近上一次FM的響應來對這些參數值進行提取，然后保持這些參數不變，重新優化 CM[6-8]，得到一組濾波器的物理尺寸參數。在FM中將這些優化參數代入驗證，重復上述步驟，直到FM結果達到設計要求。

PSO 算法是一種新的進化算法（Evolutionary Algorithm - EA），于1994年被Kennedy和Eberhart等提出，PSO算法是根據鳥類覓食行為衍生而來，設計模型的初衷是為了使鳥類的運動軌跡圖形化，在對鳥類覓食行為的無數次的實驗觀察中，發現鳥類在尋找食物的過程中會將自己的信息共享出去，其他鳥類會依據此信息來改變自己的運動[9]。PSO算法以其容易實現，收斂速度快，精度高等優點越來越多地被人們用于各種工程優化中。

1 基本理論

1.1 ISM算法

初始優化問題定義為：式中：U是一個給定的目標函數，它是表示誤差的函數；xf是需要求解的 FM參數；Rf為FM參量xf的響應。由于FM的電磁仿真需要的時間比較長，所以一般不會直接優化求解式（1），而是在 CM中進行優化，它是FM在某種程度上的近似[10-12]，CM參量響應為Rc，通過優化CM，得到CM最優解對應的系統響應為優化的過程就是不斷接近xf。

ISM算法通過建立一個xf，xc和預選參數xp之間的隱式映射Q，使

(2)式中的優化輔助參數xP可以在CM逼近第j-1步FM的參數提取中得到。在進行第j次第代中，通過將CM的響應逼近第j-1步FM響應來優化參數，使

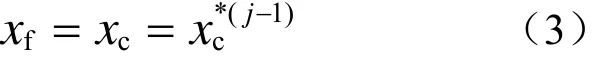
考慮到在空間映射算法中參數提取過程中的不收斂性，本文將PSO與ISM算法結合，改進了CM與FM之間的參數映射。若FM的響應達到要求，則不再進行優化過程。否則再次進行參數提取，如此循環優化直到FM的響應滿足目標[13-16]。

1.2 PSO算法

PSO算法是首先將一群粒子初始化為隨機值，然后第代找到最優解，在每一次第代中，可以通過兩個“極值”的變化來隨時更新自己的值。第一個解稱為個體極值pBest，它是粒子本身所找到的最優解。另一個解稱為全局極值gBest，它是整個種群找到的最優解。

假設在一個N維空間中有m個粒子，粒子的位置可以表示為:

陽圩農場自1956年建場以來，歷經了咖啡、橡膠、糧食、柑橘及茶葉種植等多個產業調整。1983年，農場立足資源、環境、區位條件，多方分析論證，引入芒果種植，三十多年來，不斷優化芒果品種結構，發展芒果品牌，初步呈現出區域化布局、規模化生產、產業化經營的發展格局，被農業部認定為“南亞熱帶作物名優芒果生產基地”。

xi是第i個粒子在N維空間中的位置。每一個粒子的位置都有可能是最優解，把 xi代入到一個目標函數得到的值就是其適應值，根據適應值的大小就可看出xi是否是所求的值。

記pa為第i個粒子群目前所能找到的最優位置，pg為整個粒子群目前所能找到的最優位置。粒子依據以下公式來改變自己的位置：

式中：i=1, 2,··, m,··, n=1, 2,··, N；參數c1，c2是非負常數；r1和 r2是[0:1]之間的任意數。第代停止的條件有兩個：一，第代次數達到最大第代次數；二，搜索到的最優化的位置滿足適應閾值。

1.3 參數提取的約束條件

參數提取是ISM算法的關鍵，參數提取中參數的范圍將直接影響著算法的收斂。對于ISM算法，代理模型優化參數的初始值設置的不同，得到的優化結果就不相同，導致FM逼近響應目標就有差異。經過仿真驗證在參數提取過程中引入 PSO，可以有效地減少第代次數，得到符合要求的指標。

根據PSO的啟示，可以設預提取的參數為：

設 pa為第 i個參數目前搜索到的最優值，pg為所有的預提取的參數目前搜索到的最優值。

各個參數根據以下公式來不斷調節各自的值：

式中：i=1, 2,··, m，n=1, 2,··, N；參數c1，c2是非負常數；r1和r2是[0～1]之間的任意數。

一般選取介質基板的相對介電常數εr和介質層厚度 h作為預選參數。需要注意的是，預選參數只在CM中變化，在FM中是保持不變的。將PSO用于ISM算法中的參數提取中，是改善和增強算法收斂性的一種有效手段，且不易帶來額外的誤差，保證算法的有效性。

2 雙頻濾波器設計實例

本節以一個雙頻濾波器為例，通過仿真驗證了PSO在ISM算法的參數提取過程中的有效性。

濾波器的工作頻率分別為 2.45 GHz和 5.25 GHz，其FM結構如圖1所示，為加快算法進程，減少設計參量數目，使濾波器部分參數保持不變，微帶耦合線寬度t1=0.7 mm，t2=0.6 mm，抽頭微帶線特性阻抗為50 Ω，其他設計參量為：

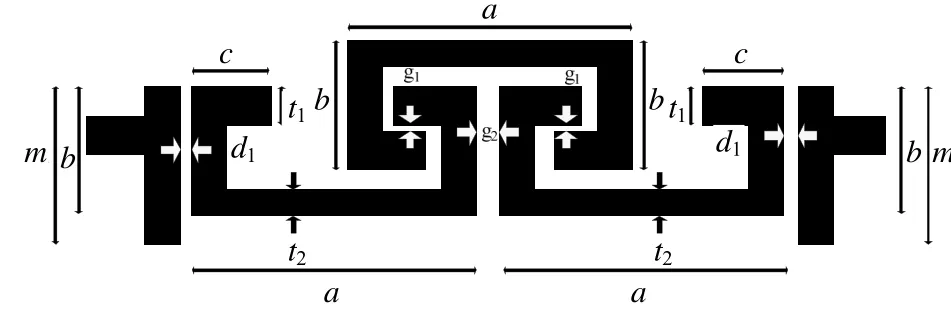
圖1 雙頻濾波器FM結構及各參數Fig.1 Dual-band filter fine model structure and parameters

所選用的介質基板的相對介電常數初始值為2.65，介質厚度為1 mm，其電路模型如圖2所示，各電路單元按照設計參量設置。預選參數為各個電路模塊的相對介電常數和厚度：

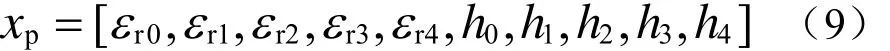
式中：εr1和h1，εr2和h2，εr3和h3分別為耦合線Clin1、 Clin2、Clin3的相對介電常數和厚度，εr4和h4為微帶線TL1的相對介電常數和厚度，εr0和h0為其他微帶線的相對介電常數和厚度，在對角線對稱的位置預選參數值相同，h單位mm。

圖2 雙頻濾波器CM結構及各參數Fig.2 Dual-band filter crude model structure and parameters

在實際仿真第代過程中，要靈活設計 CM優化的目標，使 CM能很快達到要求，將其設計參數優化值代入FM進行仿真，仿真結果如圖3所示，通過觀察S11和 S21曲線可以看出，兩個通帶中心頻率相對于 CM中的曲線均向右偏移，不滿足指標要求，需要進一步第代優化，因此進入參數提取步驟，對提取的預選參數用公式（7）處理后，保持其值不變，再次對 CM進行優化，將得到的優化參數值導入到HFSS中進行驗證，如此循環第代直到達到設計指標要求，完成整個算法流程。3次第代的過程如圖4所示，第代過程中設計參量的值如表1所示。

圖3 兩個模型初始計算結果Fig.3 A model for the two initial results

圖4 三次第代的響應結果Fig.4 Response result of three iterations

表1 濾波器設計參數優化值Tab.1 Filter design parameters optimal values

為使分析具有實際性和針對性，對第三次第代后的數據進行精度的取舍，得到雙頻濾波器最佳的設計參數為：a=14.8 mm，b=8.4 mm，c=3 mm，d1=0.1 mm，g1=0.46 mm，g2=0.1 mm，m=10 mm，n=1 mm。第三次第代后的響應結果圖5所示。

圖5 參數微調后的濾波器響應Fig.5 Parameters tuning the filter response

可以看出，濾波器兩個中心頻率分別約在 2.45 GHz和5.25 GHz，3 dB相對帶寬分別為2.94%和6.09%，帶內回波損耗大于18 dB，帶外抑制性能良好，能用于IEEE 802.11 b/a頻段。用本文算法設計的雙頻濾波器指標與常用方法設計的基本無差異，但是使用本文算法設計濾波器的時候第代次數會大大減少，由于每次第代耗時較長，所以使用本文算法會大大減少濾波器的設計時間。

3 結論

主要研究了將PSO應用到ISM算法的參數提取中，并以一個中心頻率為2.45 GHz和5.25 GHz的微帶雙頻段濾波器進行驗證。在 ISM 算法沒有引入PSO時，每次第代優化時的參數值往往變化較大，通過引入PSO對參數提取中參數的范圍施加限制約束條件，使得每次第代優化時的參數值不再出現較大幅度的變化，有效地改善了第代過程中算法的收斂性，并通過仿真驗證了算法的有效性和準確性。

[1] BANDLER J W, CHEN S H. Space mapping technique for electromagnetic optimization [J]. IEEE Trans Microwave Theory Tech, 1994, 42(12): 2536-2544.

[2] BANDLER J W, CHEN S H. Electromagnetic optimization exploiting aggressive space mapping [J]. IEEE Trans Microwave Theory Tech, 1995, 43(12): 2874-2882.

[3] BANDLER J W, CHEN S H. Implicit space mapping optimization exploiting preassigned parameters [J]. IEEE Trans Microwave Theory Tech, 2004, 52(1): 378-385.

[4] CHEN S H, BANDLER J W. A statistical input space mapping approach for accommodating modeling residuals [J]. IEEE MTT-S Int Microwave Symp Digest (IMS), 2014, 36(5): 1-3.

[5] CHEN S H, BANDLER J W. Fast EM modeling exploiting shape-preserving response prediction and space mapping [J]. IEEE Trans Microwave Theory Tech, 2015, 62(3): 399-407.

[6] ZHU J, BANDLER J W. Antenna optimization through space mapping [J]. IEEE Trans Antennas Propagation, 2007, 55(3): 651-658.

[7] TU S, CHEN S H, ZHANG Y F, et al. Space mapping optimization of handset antennas exploiting thin-wire models [J]. IEEE Trans Antennas Propagation, 2014, 61(7): 3797-3807.

[8] KOZIEL S, BANDLER J W. Implicit space mapping with adaptive selection of preassigned parameters [J]. IET Microwaves Antennas Propagation, 2010, 4(3): 361-373.

[9] NGUYEN T, MORISHITA H, KOYANAGI Y, et al. A multi-level optimization method using PSO for the optimal design of an L-shaped folded monopole antenna array [J]. IEEE Trans Antennas Propagation, 2014, 62(1): 206-215.

[10] KOZIEL S, BANDLER J W, CHEN Q S. Constrained parameter extraction for microwave design optimisation using implicit space mapping [J]. IET Microwaves Antennas Propagation, 2011, 5(10): 1156-1163.

[11] XING L F, LEI Z Y, XIE Y J, et al. A new implicit space mapping with high convergence for microwave filter design [J]. J Electron Inf Technol, 2011, 48(3): 744-748.

[12] ZHANG G X, ZHAO H L. Optimization of microstrip dual-band filter with implicit space mapping algorithm [C]//2011 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). New York: IEEE, 2011.

[13] SU J R, YAO C H. Design of dual-band filters with arc patch based on square loop structure [C]// The 7th International Conference on Computer Science & Education (ICCSE). New York: IEEE, 2012.

[14] SU J R, YAO C H. Design of dual-band filters with arc patch based on square loop structure [C]// International Conference on Computer Science & Education (ICCSE). New York: IEEE, 2012.

[15] LI Z, RAHMAT Y. Optimization of PIFA-IFA combination in handset antenna designs [J]. Antennas Propagation IEEE Trans, 2015, 53(5): 1770-1778.

[16] KIM K J, AHN K H. The high isolation dual-band inverted F antenna diversity system with the small N-section resonators on the ground plane [J]. Microwave Opt Technol Lett, 2007, 49(3): 731-734.

（編輯：曾革）

Particle swarm implicit space mapping algorithm design of dual-band filter

ZHANG Youjun, WANG Liandong

(School of Information Engineering, Shanghai Maritime University, Shanghai 201306, China)

The particle swarm optimization (PSO) algorithm used in implicit space mapping (ISM) parameter extraction can improve the dis-convergence of the parameter extraction algorithm. This paper first introduced PSO in parameter extraction, and the main aim of the research was to improve the ISM algorithm. It is found that improving the parameter mapping in the ISM algorithm between the coarse model (CM) and the fine model (FM) significantly reduces the number of iterations. Take the dual-mode filter as a for example, by using the PSO algorithm of ISM a micro-strip dual-frequency band filter worked in the wireless local area network (WLAN) spectrum was designed, whose center frequencies were 2.45 GHz and 5.25 GHz, respectively. After three iterations and fine-tuning, the filter reached the design target. Thus, the introduction of PSO significantly reduces the number of simulations in the FM, and effectively improves the design efficiency of the filter.

particle swarm optimization; implicit space mapping; parameter extraction; coarse model; fine model; dual-band filter

10.14106/j.cnki.1001-2028.2016.12.013

TN713; TP391

A

1001-2028（2016）12-0057-04

2016-09-28

王連棟

國家自然科學基金資助項目（No. 61131002）

張友俊（1961-），男，江蘇揚州人，教授，主要從事微波技術的研究，E-mail: yjzhang@cie.shmtu.edu.cn ；

王連棟（1991-），男，安徽亳州人，研究生，主要從事空間映射算法方面的研究，E-mail: wangliandong917@163.com 。

時間：2016-11-29 11:41:40

http://www.cnki.net/kcms/detail/51.1241.TN.20161129.1141.013.html