基于云模型的多狀態系統可靠性評估

高 龍， 宋太亮， 閆 旭

(1. 裝甲兵工程學院技術保障工程系， 北京 100072； 2. 中國國防科技信息中心， 北京 100142)

基于云模型的多狀態系統可靠性評估

高 龍1， 宋太亮2， 閆 旭1

(1. 裝甲兵工程學院技術保障工程系， 北京 100072； 2. 中國國防科技信息中心， 北京 100142)

針對多狀態系統可靠性評估中存在的不確定性問題，研究了采用云模型表示狀態概率的隨機不確定性和認知不確定性的多狀態系統可靠性評估方法。基于狀態概率云模型進一步擴展了通用生成函數(Universal Generating Function ，UGF)，形成了云通用生成函數(Cloud Universal Generating Function ，CUGF)，并定義了其2種基本運算，給出了在給定需求下多狀態系統可用度的求解步驟以及云模型表示系統可用度的3個云數字特征。最后，通過3單元串-并聯多狀態系統算例及其與基于概率理論的評估結果的比較，驗證了方法的準確性和可行性。研究成果為多狀態系統可靠性評估中信息或數據的不完整性、不精確性及模糊性等的處理提供了新的思路和方法。

多狀態系統；可靠性評估；云模型；不確定性

多狀態系統可靠性研究是近幾年國內外研究的主流方向之一。Murchland[1]提出并完善了多狀態系統可靠性的基本概念。目前，多狀態系統可靠性的相關概念和理論已廣泛用于機械[2]、電力[3-4]和網絡[5-7]等領域。多狀態系統可靠性評估主要基于結構函數法[8]、隨機過程法[9]、Monte Carlo仿真[10]以及通用生成函數法(Universal Generating Function，UGF)[5]4種方法，應用這些方法的基本前提條件為：1)構成多狀態系統的單元或子系統的每個狀態可利用統計概率完全表征；2)可精確獲得多狀態系統的單元或子系統的所有性能水平。但由于數據與信息的不精確和不充分等不確定因素，實踐中很難對狀態概率和性能水平進行處理，進而影響了評估結果的準確性和可信性。因此，在多狀態系統可靠性評估中需要對單元或子系統的狀態概率和性能水平的各種不確定性進行建模。不確定性可分為隨機不確定性和認知不確定性[11]，其中隨機不確定性主要來自部件行為的可變性和隨機性；認知不確定性主要來自知識或數據的不完整性和不精確性[12]。Destercke等[13]應用信任函數表示認知不確定性并擴展了UGF來評估多狀態系統的可靠性。雖然信任函數中的概率指派函數可有效刻畫信息的不完整性，但該方法并不適用于信息具有模糊性的多狀態系統可靠性評估。Li等[14]基于模糊集合理論，應用隨機模糊變量綜合考慮隨機不確定性和認知不確定性,對多狀態系統可靠性進行了評估。該方法雖然解決了2種不確定性共存的問題，但卻丟失了單元或子系統的部分細節信息,且計算過程較為復雜。

根據單元或子系統的物理特性、歷史數據以及專家經驗等信息，可對多狀態系統的有關特性進行估計并給出相應的偏好值，則所有信息來源給出的偏好值集合就構成了該特性的一個云，可應用云理論對整個多態系統的行為進行進一步研究。雖然單個偏好值是確定的，但是由偏好值集合構成的云卻蘊含了單元特性的隨機不確定性和認知不確定性。筆者基于云理論的基本思想，針對多狀態系統可靠性評估中不確定性問題，應用云模型來表示狀態概率的不確定性，建立云通用生成函數(Cloud Universal Generating Function ，CUGF)并定義相應的運算，給出在給定需求下多狀態系統的穩態可用度評估步驟以及可用度云的3個數字特征值，并通過算例進行驗證。

1 基本理論與假設

1.1 多狀態系統理論

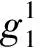
1.2 云理論

1.2.1 云的定義

設U={x}為以精確數值表示的論域，A為與之對應的定性概念，x∈U存在一個有穩定傾向的隨機數y=μA(x)，并稱之為x對A的隸屬度，隸屬度y在論域U上的分布稱為隸屬云(簡稱“云”)[15]，(x,y)稱為云滴。云是定性概念與定量數值之間的轉換模型，成千上萬的云滴組成云，云滴是對定性概念的定量描述，云滴的產生過程表示了定性與定量之間的相互映射。

1.2.2 云的數字特征

云通過期望值Ex、熵En和超熵He三個數字特征值來定量表示。其中：Ex為論域的中心值，可表示定性概念；En為定性概念模糊程度的測度，反映了在論域中被概念所接受的數值范圍，En越大，概念的數值范圍就越大，模糊程度就越大；He為熵的熵，可反映云滴的離散程度，也是隸屬度隨機性的測度，He越大，表明云滴越厚，離散程度也越大。

1.2.3 正向正態云發生器

由數字特征產生云滴進而構成云的過程稱為正向云發生器。由于正態云模型具有普適性[16]，因此筆者選擇正態云模型來描述信息的不確定性。設云滴數量為m，則產生m個云滴(xl,μl)(l=1,2,…,m)的正態云的具體步驟如下：

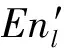
1.2.4 逆向正態云發生器

逆向正態云發生器是根據一定數量的正態分布云滴得到云的3個數字特征值的過程。逆向正態云發生器算法是基于統計原理，分為包含確定度信息和不包含確定度信息2類。筆者采用Liu等[17]提出的不包含確定度信息的算法。設有m個樣本點xl(l=1,2,…,m)，則得到該云的3個數字特征值的步驟如下：

1.3 基本假設

假設1：單元或系統具有有限個離散狀態，且各狀態都是確定的，即各狀態相應的性能水平不具有隨機性和模糊性。

假設2：單元或系統的狀態概率具有不確定性，可用正態云模型對其特征進行描述。

假設3：對于每個狀態概率，存在多個與其有關的信息來源，且每個來源的信息均能給出一個偏好值。

2 基于UGF的多狀態系統評估

可靠性分析的復雜性隨著單元數量n的增加呈指數增長的趨勢，而通用生成函數通過利用系統模塊化的優勢可在一定程度上降低該指數的增長趨勢。

目前，主要利用所有單元性能水平的概率分布來研究系統結構函數。當給定概率pj時，單元j的狀態信息的z變換函數為

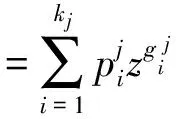
式中：變量z用于提供多項式算子，單元或系統的性能水平信息存貯于指數項中。整個系統的UGF為

U(z)=Ωφ(U1(z),…,Un(z))=

由此可以看出：UGF是一種基于z變換和通用合成運算的方法。在合成運算中，系統結構函數φ(g)為整個系統的性能水平，由不同單元的性能水平構成。在可靠性邏輯框圖中，φ(g)通過單元之間的連接形式(串聯或并聯等)來嚴格定義[18]。

系統性能水平和需求w之間的關系通常利用系統狀態滿足指標ri的情況來確定，即ri=gi-w。當且僅當ri≥0時，狀態i是一個可接受的狀態。通常，多狀態系統的可用度可定義為多狀態系統的性能水平大于需求的概率，即

對于給定的U(z)和w，應用運算δA可獲得多狀態系統的穩態可用度，即

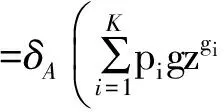
3 云模型表示不確定性的CUGF

由上述基于概率論的評估過程可以看出：定義在空間狀態gj上的概率pj描述了單元狀態出現的隨機不確定性。然而，確定單元狀態概率pj的值需要大量的數據，特別是在各種不確定性同時存在的情況下，如數據缺失或不精確、小樣本以及專家意見等，概率論難以對這些不確定性進行建模。因此，筆者應用云模型來表示狀態概率的不確定性。

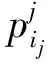
應用云模型表示單元狀態概率不確定性時，若給定單元j的概率云Cpj(Ex,En,He)時，則單元信息的z變換函數為

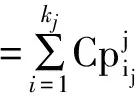
式中：變量z用于提供多項式算子，單元的性能水平信息存貯于指數項中，這與UGF相類似。整個系統的CUGF為

U(z)=Ωφ(U1(z),…,Un(z))=

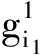
設Cp1(Ex1,En1,He1)和Cp2(Ex2,En2,He2)為任意2個正態概率云，其運算結果為正態概率云Cp(Ex,En,He)，則依據文獻[19]定義運算規則如下：

1)當Cp(Ex,En,He)=Cp1(Ex1,En1,He1)+Cp2(Ex2,En2,He2)時，有

2)當Cp(Ex,En,He)=Cp1(Ex1,En1,He1)×Cp2(Ex2,En2,He2)時，有

得到多狀態系統基于云模型的CUGF后，便可應用運算δA計算出多狀態系統的穩態可用度，即

4 算例分析

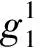
φ(G1(t),G2(t),G3(t))=

φS(φP(G1(t),G2(t)),G3(t))=

min((G1(t)+G2(t)),G3(t)),

式中：φS為串聯運算；φP為并聯運算。整個系統的UGF為

U(z)=Ωφ(u1(z),u2(z),u3(z))=

ΩφS(ΩφP(u1(z),u2(z)),u3(z))。

圖1 流體傳動系統結構

4.1 基于概率的穩態可用度

A(1.5)=δA(U(z),1.5)=δA(0.56gz3.5+0.23gz3

+…+0.009 6gz1+0.049 6gz0,1.5)=

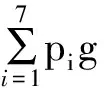
0.067 2+0.096+0+0=0.940 8。

4.2 基于云模型的穩態可用度

設單元j的每個狀態有200個信息來源，每個信息來源可給出一個狀態概率偏好值，則所有偏好值構成樣本集合X={x1,x2,…,x200}，采用1.2.4節中不包含確定度信息的逆向正態云生成器算法，求得每個概率云的3個數字特征值Ex、En和He，如表1所示。采用1.2.3節中的正向正態云發生器算法求得3個單元概率云的云滴以及正態云圖，如圖2-4所示。

表1 云概率的數字特征值

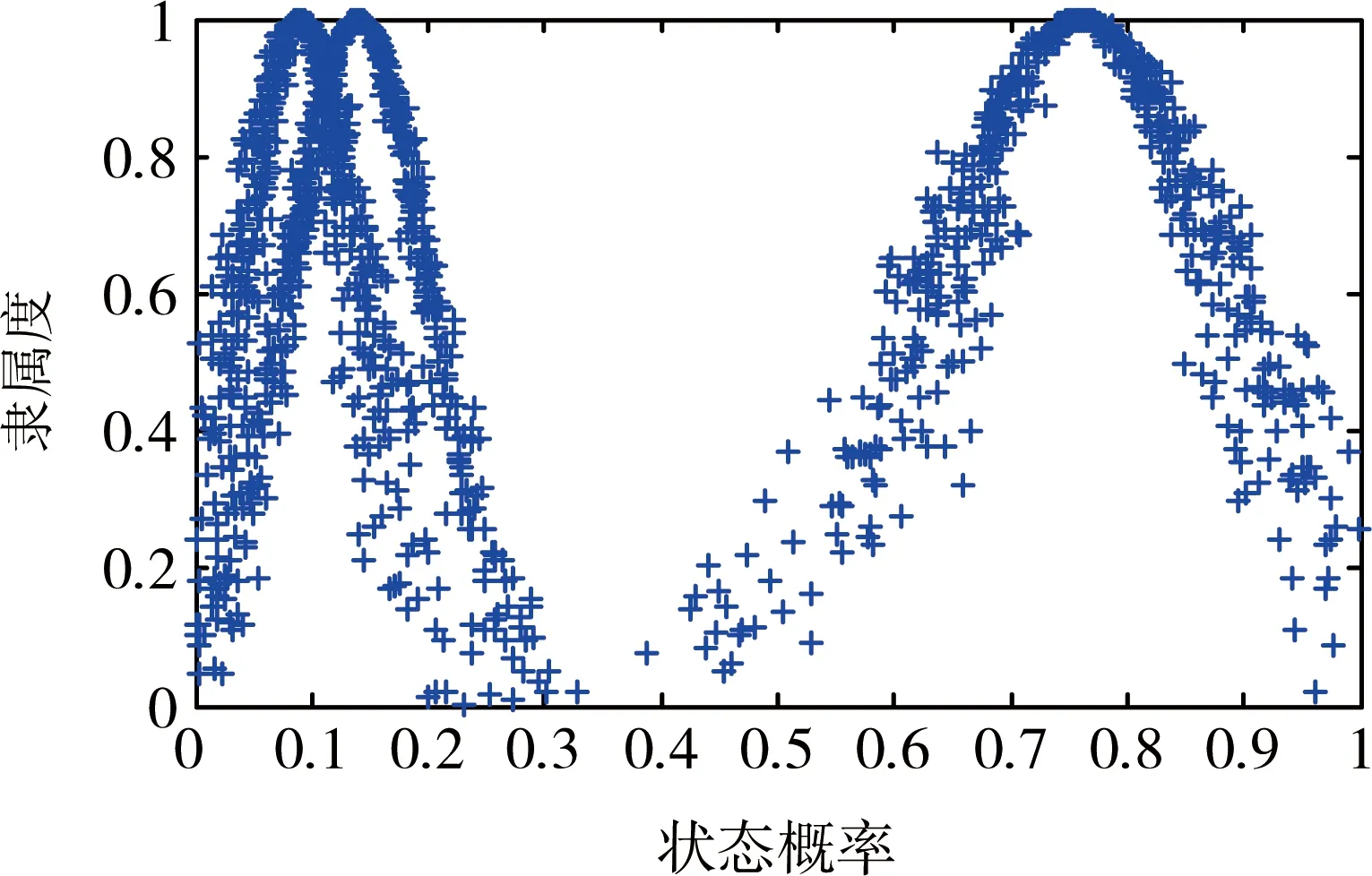
圖2 單元1的狀態概率正態云

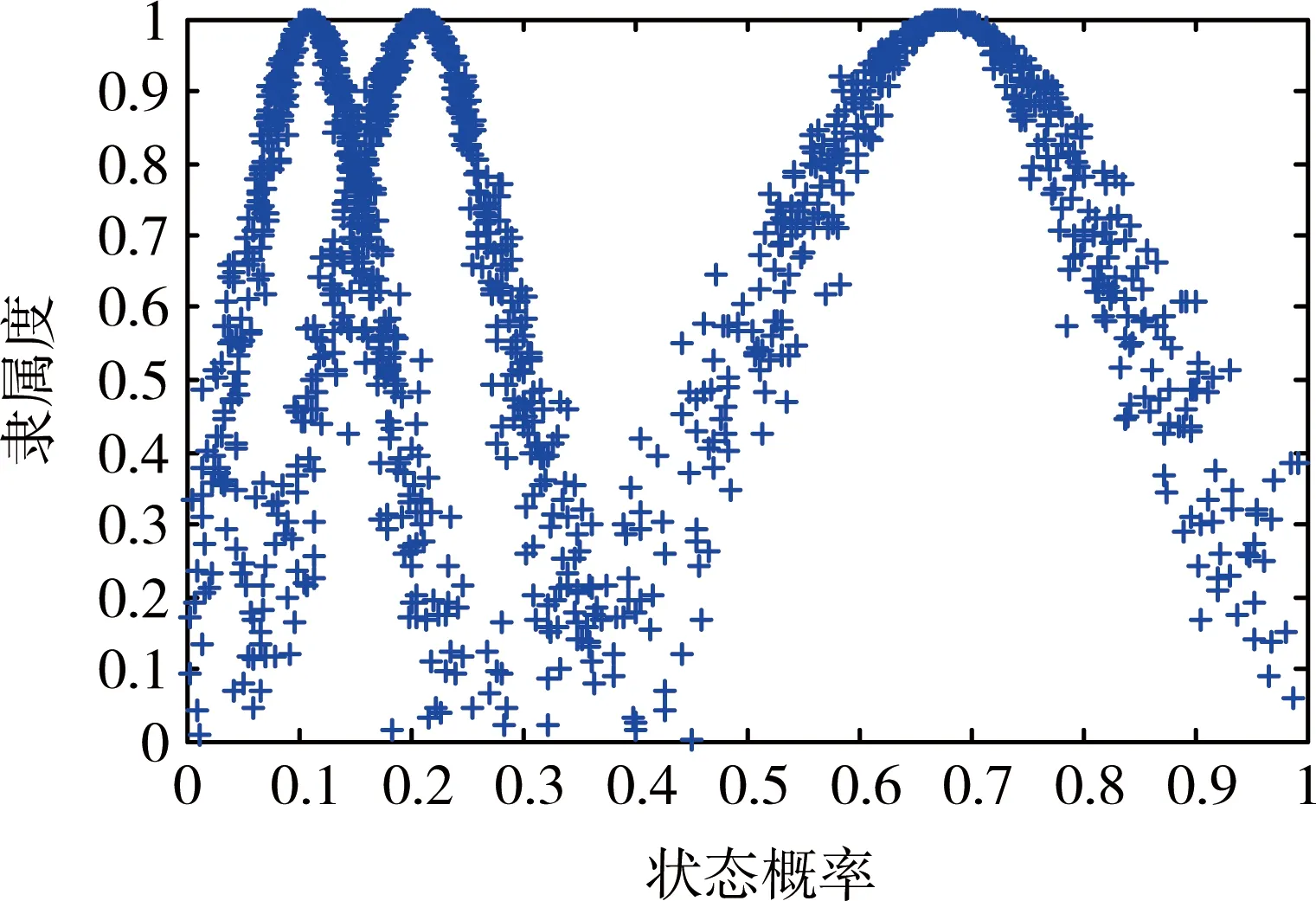
圖3 單元2的狀態概率正態云

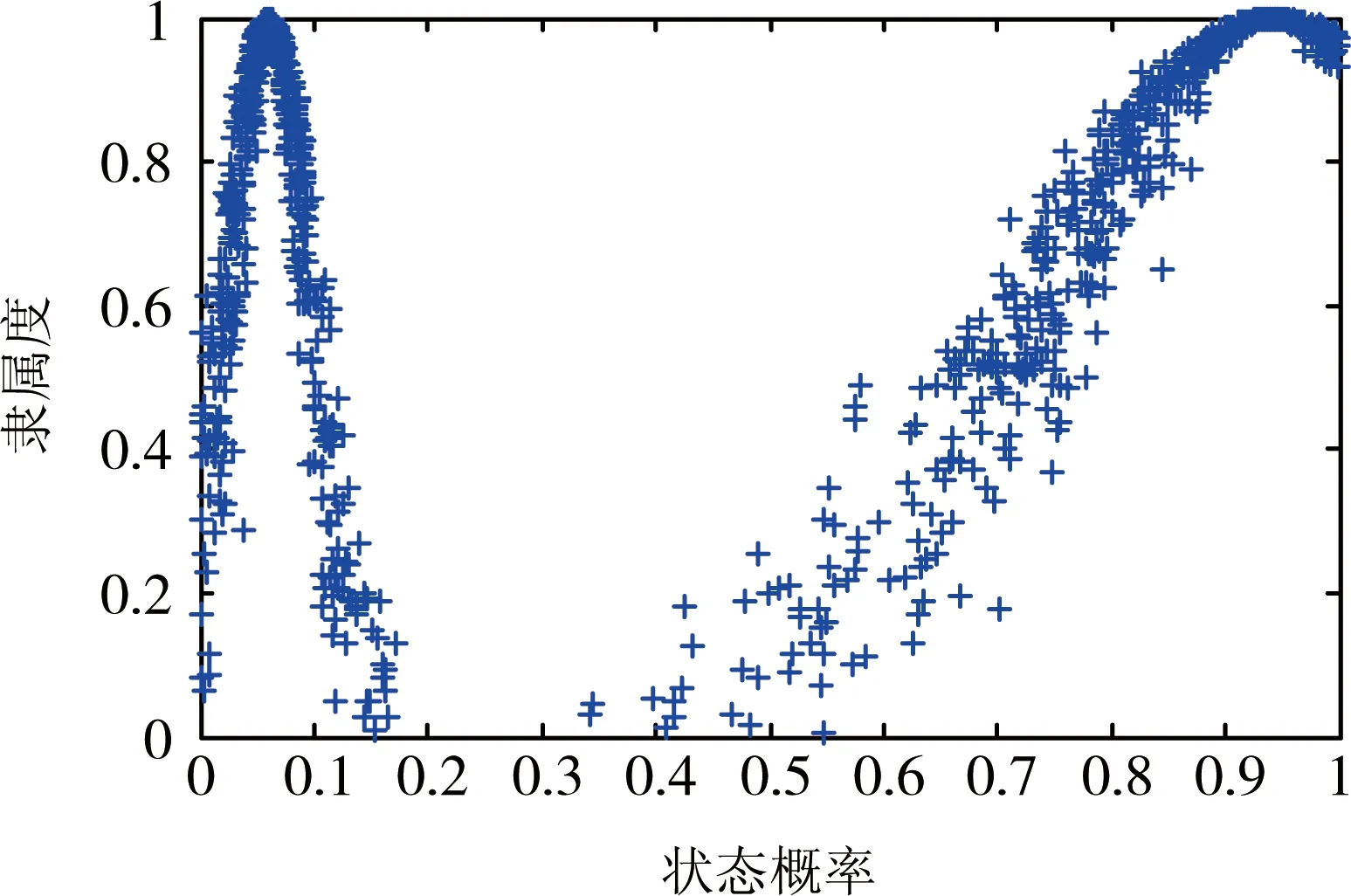
圖4 單元3的狀態概率正態云

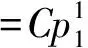
(0.77,0.124 6,0.023 78)gz1.5+

(0.14,0.062 3,0.006 92)gz1+

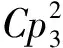
(0.68,0.114 5,0.031 42)gz2+

(0.21,0.076 5,0.010 62)gz1.5+

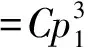
(0.94,0.201 3,0.034 12)gz4+

(0.06,0.036 7,0.008 32)gz0。

為了方便編程，應用矩陣來表示各個具有多狀態的單元變換函數，其中矩陣的列依次分別為單元各個狀態的Ex、En和He，具體如下：

各矩陣之間的運算采用根據前文所定義的運算規則下的特定運算。由于單元1和單元2是并聯的，所以采用并聯結構函φP來進一步獲得二者的CUGF，即

ΩφP(u1(z),u2(z))=

由于單元1和單元2所組成的子系統與單元3是串聯，因此整個系統的CUGF為

U(z)=ΩφS(ΩφP(u1(z),u2(z)),u3(z))=

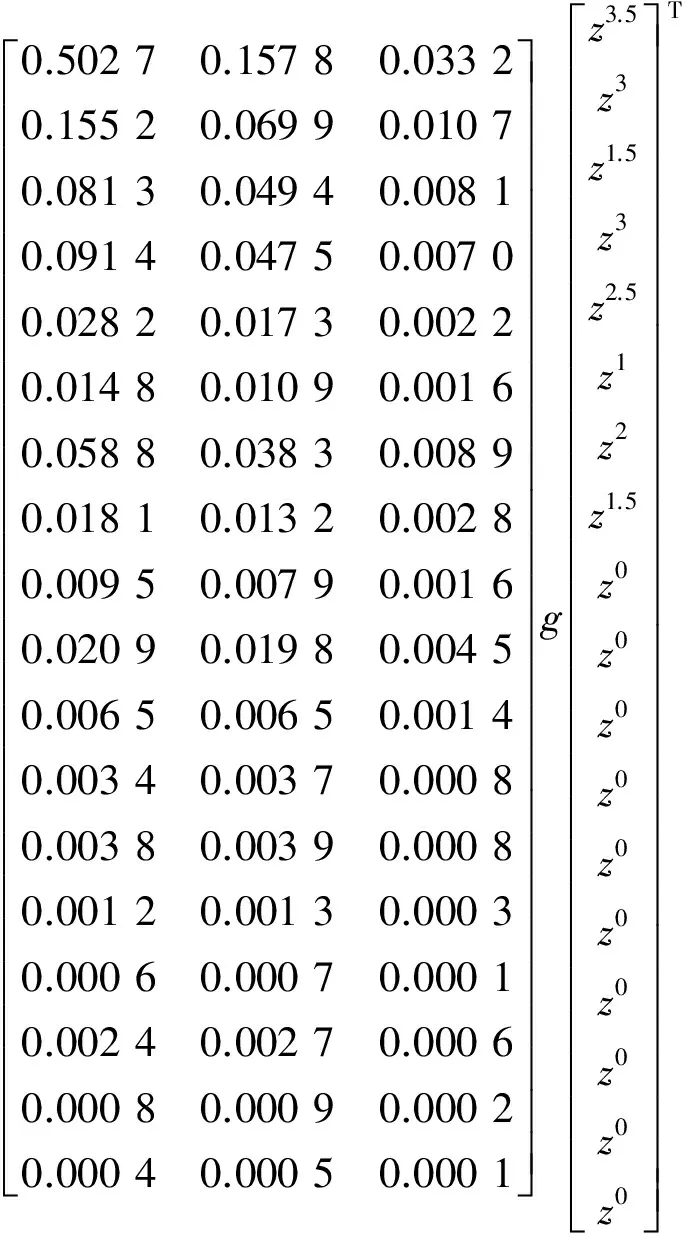
為簡化計算，計算過程中可將指數相同的項先合并，然后再計算，但為了程序處理方便，筆者采用先計算后合并的方式。當w=1.5時，該多狀態系統的可用度為

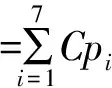
(0.502 7,0.157 8,0.033 2)+(0.155 2,0.069 9,0.010 7)+

(0.081 3,0.049 4,0.008 1)+(0.091 4,0.047 5,0.007 0)+

(0.028 2,0.017 3,0.002 2)+(0.058 8,0.038 3,0.008 9)+

(0.018 1,0.013 2,0.002 8)=(0.937 8,0.024 1,0.003 6)。

由此可見：在給定需求的情況下，該多狀態系統的穩態可用度云的期望值為0.935 7，與概率情況下該系統的可用度0.940 8相比稍小，但非常接近且都大于所要求的可用度0.9。采用1.2.3節中的正向正態云發生器算法可求出該可用度的云滴，其正態云如圖5所示。

圖5 多態系統穩態可用度正態云

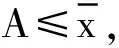
在本算例中，評估得到的穩態可用度云為(0.937 8,0.024 1,0.003 6)，對該結果判定如下：

Ex-3En=0.937 8-3×0.024 1=0.865 5，

Ex+3En=0.937 8+3×0.024 1=1.010 1，

故當A=0.9時，

Ex-3En≤A≤Ex+3En。

5 結論

針對多狀態系統可靠性評估中的不確定性建模問題，提出了應用云模型表示單元或子系統狀態概率的隨機不確定性和認知不確定性。在概率云模型的基礎上擴展了通用生成函數，并給出了多狀態系統在給定需求下的系統穩態可用度的求解過程以及可用度云的3個數字特征值。得出的系統穩態可用度云不僅能夠定量描述系統可用度，同時還保留了系統可用度的更多細節信息，評估結果準確、可信。筆者提出的研究思路和方法為存在信息或數據的不完整性、不精確性及模糊性的多狀態系統可靠性評估提供了一定的借鑒，但在研究中主要考慮了狀態概率的不確定性問題，并未涉及單元和子系統的狀態存在不確定性的情況，下一步研究將同時考慮單元和子系統的狀態和狀態概率的不確定性。

[1] Murchland J D.Fundamental Concepts and Relations for Reliability Analysis of Multi-state Systems and Fault Tree Analysis[C]∥Theoretical and Applied Aspects of System Reliability and Fault Tree Analysis,Philadelphia：SIAM,1975：581-618．

[2] Krzysztof K， Joanna S.On Multi-state Safety Analysis in Shipping [J]． International Journal of Reliability， Quality and Safety Engineering， 2007，14(6)：547-567．

[3] Massim Y， Zeblah A， Meziane R， et al．Optimal Design and Reliability Evaluation of Multi-state Series-parallel Power Systems[J]． Nonlinear Dynamics，2005，40(4)：309-321．

[4] Taboada H A， Espiritu J F， Coit D W．Design Allocation of Multi-state Series-parallel Systems for Power Systems Planning： A Multiple Objective Evolutionary Approach[J]．Journal of Risk and Reliability， 2008， 222(3)：381-391．

[5] Yeh W C． A Simple Universal Generating Function Method for Estimating the Reliability of General Multi-state Node Networks[J]． IIE Transactions， 2008， 41(1)： 3-11．

[6] 黃寧， 伍志韜． 網絡可靠性評估模型與算法綜述[J]． 系統工程與電子技術， 2013， 35(12)： 2651-2657．

[7] Gianni C, Emilio G, Fabrizio P, et al． Reliability Assessment in Smart Distribution Networks [J]．Electric Power Systems Research, 2013, 104：164-175．

[8] Zaitseva E, Kovalik S, Levashenko V, et al．Algorithm for Dynamic Analysis of Multi-State System by Structure Function[C]∥Proceedings of the IEEE International Conference on Computer as a Tool, Belgrade：EUROCON, 2005： 1224-1227．

[9] Lisnianski A. Extended Block Diagram Method for a Multi-state System Reliability Assessment[J]． Reliability Engineering & System Safety， 2007， 92(12) ： 1601-1607．

[10] Zio E, Marella M, Podofillini L．A Monte Carlo Simulation Approach to the Availability Assessment of Multi-state Systems with Operational Dependencies[J]．Reliability Engineering & System Safety， 2007， 92(7)： 871- 882．

[11] Li Y F， Zio E． Uncertainty Analysis of the Adequacy Assessment Model of a Distributed Generation System[J]． Renewable Energy, 2012, 41(1)：235-244．

[12] Drouin M. Guidance on the Treatment of Uncertainties Associated with PRAs in Risk-informed Decision Making: Main Report[R]. US：Nuclear Regulatory Commission,2009．

[13] Destercke S, Sallak M. An Extension of Universal Generating Function in Multi-state Systems Considering Epistemic Uncertainties[J]. IEEE Transactions on Reliability, 2013, 62(2)：504-514．

[14] Li Y F, Ding Y, Zio E. Random Fuzzy Extension of the Universal Generating Function Approach for the Reliability Assessment of Multi-State Systems under Aleatory and Epistemic Uncertainties[J]. IEEE Transactions on Reliability, 2014, 63(1)： 13-25．

[15] 李德毅, 杜鹢． 不確定性人工智能[M]. 北京：國防工業出版社, 2005： 229-230．

[16] 李德毅, 劉常昱.論正態云模型的普適性[J]. 中國工程科學, 2004, 6(8)： 28-34．

[17] Liu C Y, Feng M, Dai X J, et al. A New Algorithm of Backward Cloud[J]. Journal of System Simulation, 2004, 16(11)：2417-2420．

[18] Levitin G, Lisnianski A. Multi-state System Reliability Assessment, Optimization, Applications[M].London：Springer London, 2003：61-90.

[19] Shi Y B, Liu H, Sun J. The Cloud Model Based on Grey System Theory and Application on Effectiveness Evaluation[C]∥Intelligent Computing Theories. Nanning：Springer, 2013：31-38．

[20] Ding Y, Lisnianski A. Fuzzy Universal Generating Functions for Multi-state System Reliability Assessment[J]. Fuzzy Sets and Systems, 2008, 159(3)： 307-324．

[21] 湯永利, 徐國愛, 鈕心忻, 等.基于信息熵的信息安全風險分析模型[J]． 北京郵電大學學報， 2008， 31(2)： 50-53．

(責任編輯:王生鳳)

Reliability Assessment of Multi-state Systems Based on Cloud Model

GAO Long1, SONG Tai-liang2, YAN Xu1

(1. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China； 2. Defense Science Technology Information Center, Beijing 100142, China)

This paper studies the method of reliability evaluation of the multi-state systems aimed at the problems of uncertainties, in which the uncertainties of aleatory and epistemic of the state probability are presented by the cloud model. The Universal Generating Function (UGF) is further expanded on the basis of the cloud probability model, then a Cloud Universal Generating Function (CUGF) is formed, its two kinds of operations are defined, and the process of the solution and three cloud digital features of the cloud model of the availability for the multi-state systems in a given demand are provided. Finally, the accuracy and feasibility are verified by the examples of series-parallel multi-state system of the 3-unit and comparision of the assessment result based on probability theory. The research provides a new thought and method to deal with the incomplete, inaccuracy, fuzzy information and data in reliability evaluation of the multi-state systems.

multi-state systems; reliability evaluation; cloud model; uncertainty

1672-1497(2016)05-0100-07

2016-06-13

軍隊科研計劃項目

高 龍(1988-)，男，博士研究生。

TB114.3

A

10.3969/j.issn.1672-1497.2016.05.021