基于人工神經網絡的蒸汽壓縮制冷系統建模方法

楊永利， 叢 華， 江鵬程， 馮輔周

(1. 裝甲兵工程學院機械工程系， 北京 100072; 2. 裝甲兵工程學院科研部， 北京 100072)

基于人工神經網絡的蒸汽壓縮制冷系統建模方法

楊永利1， 叢 華2， 江鵬程1， 馮輔周1

(1. 裝甲兵工程學院機械工程系， 北京 100072; 2. 裝甲兵工程學院科研部， 北京 100072)

針對傳統蒸汽壓縮制冷系統建模方法運算量大且建模精度難以保證的問題，研究了基于人工神經網絡的建模方法。結合蒸汽壓縮制冷系統實際特點，研究并確定了訓練數據、網絡結構等要素，分析了網絡訓練算法。利用Levenberg-Marquardt(LM)法和最速下降法2種典型網絡訓練算法分別對神經網絡參數進行尋優，比較了2種算法的優劣。最后，將所建網絡模型應用于蒸汽壓縮制冷系統輸出變量的預測，結果表明：該網絡模型預測精度較高，說明建模方法有效。

蒸汽壓縮制冷系統； 人工神經網絡； 建模； 最速下降法； LM法

蒸汽壓縮制冷系統(以下簡稱“制冷系統”)能實現降溫及除濕功能，是空調系統的關鍵組成部分[1]，其結構和工作原理較為復雜，建立其模型有助于其優化設計和精確控制。制冷系統的建模方法主要分為物理方法和實驗方法。物理方法基于熱力學理論，需要確定眾多的參數，所建模型運算速度慢且準確性難以保證[2]。實驗方法利用實驗數據擬合系統內部變量間的關系，具有建模簡單、模型運算速度快等優點，其中，人工神經網絡(Artificial Neural Network，ANN)是一種模擬大腦學習的智能技術，對非線性和耦合系統具有很強的擬合能力，在制冷系統建模方面具有很大的優勢[3-9]。因此，筆者基于ANN理論，對蒸汽壓縮制冷系統建模方法進行系統研究，并通過將所建模型用于制冷系統出口狀態的預測來驗證建模方法的有效性。

1 制冷系統簡介及實驗數據

1.1 制冷系統簡介

蒸汽壓縮制冷系統主要由蒸發器、壓縮機、冷凝器、節流閥(亦稱膨脹閥)以及制冷劑構成，如圖1所示。蒸氣壓縮制冷系統的工作過程為:從冷凝器流出的液態制冷劑經過節流閥時壓力和溫度降低，而后流入蒸發器；在蒸發器內制冷劑吸熱，由液態變為氣態，此過程中溫度和壓力不變；從蒸發器流出的氣態制冷劑流入壓縮機，被壓縮為高溫、高壓的氣體(為保證過熱度，不能有液體出現)；而后氣態蒸發劑在冷凝器內被定壓冷卻為液態蒸發劑；處理空氣在蒸發器內借助銅管與低溫的制冷劑完成熱傳遞，從而實現降溫。

圖1 蒸氣壓縮制冷系統結構

1.2 實驗數據的獲取

從實際需求出發，制冷系統的建模一般是在處理空氣入口狀態、冷卻空氣狀態以及壓縮機轉速已知時，對處理空氣出口狀態進行預測。需要說明的是：由于膨脹閥開度起著保證制冷劑過熱度的作用，一般不對其進行直接控制，而由其自帶的控制器進行控制；同時，由于壓縮機轉速與制冷劑流量高度線性相關，故此處建模不考慮膨脹閥開度和制冷劑流量。

根據制冷系統的變量間關系，選取處理空氣入口溫度Tair,pro,in,db和相對濕度φair,pro,in、冷卻空氣溫度Tair,cds,in,db和壓縮機轉速Ncps為神經網絡輸入，選取處理空氣出口干球溫度Tair,pro,out,db和相對濕度φair,pro,out表示其出口狀態。根據實際需求，選擇實驗工況范圍如表1所示。在申菱環境有限公司的焓差法實驗臺開展了實驗，實驗中處理空氣風量為3 000 m3/h，制冷劑為R410A(總質量為10 kg)，壓縮機型號為谷輪VPV038SE。

表1 實驗工況范圍

由于實驗室設備的高能耗和大滯后性給獲得大量實驗數據帶來一定難度，因此本實驗共測試了60組數據，其中：40組數據用于訓練網絡；20組數據用于檢驗網絡的預測精度。

2 制冷系統建模

完整的網絡系統模型包括傳遞函數、模型結構(網絡層數和神經元個數)以及訓練算法。具體建模過程如下：

1)傳遞函數的確定。選擇隱含層和輸出層的傳遞函數分別為tansig和purelin。

2)網絡結構的確定。為不失一般性，本文僅建立處理空氣出口干球溫度網絡模型。結合上文研究，確定處理空氣出口干球濕度網絡模型結構如圖2所示。其中，已將處理空氣入口相對濕度φair,pro,in換算為相應的濕球溫度Tair,pro,in,wb。單隱含層神經網絡已能滿足所有系統的建模需求，還減小了網絡陷入過擬合的風險，制冷系統的網絡模型采用單隱含層結構[10]。

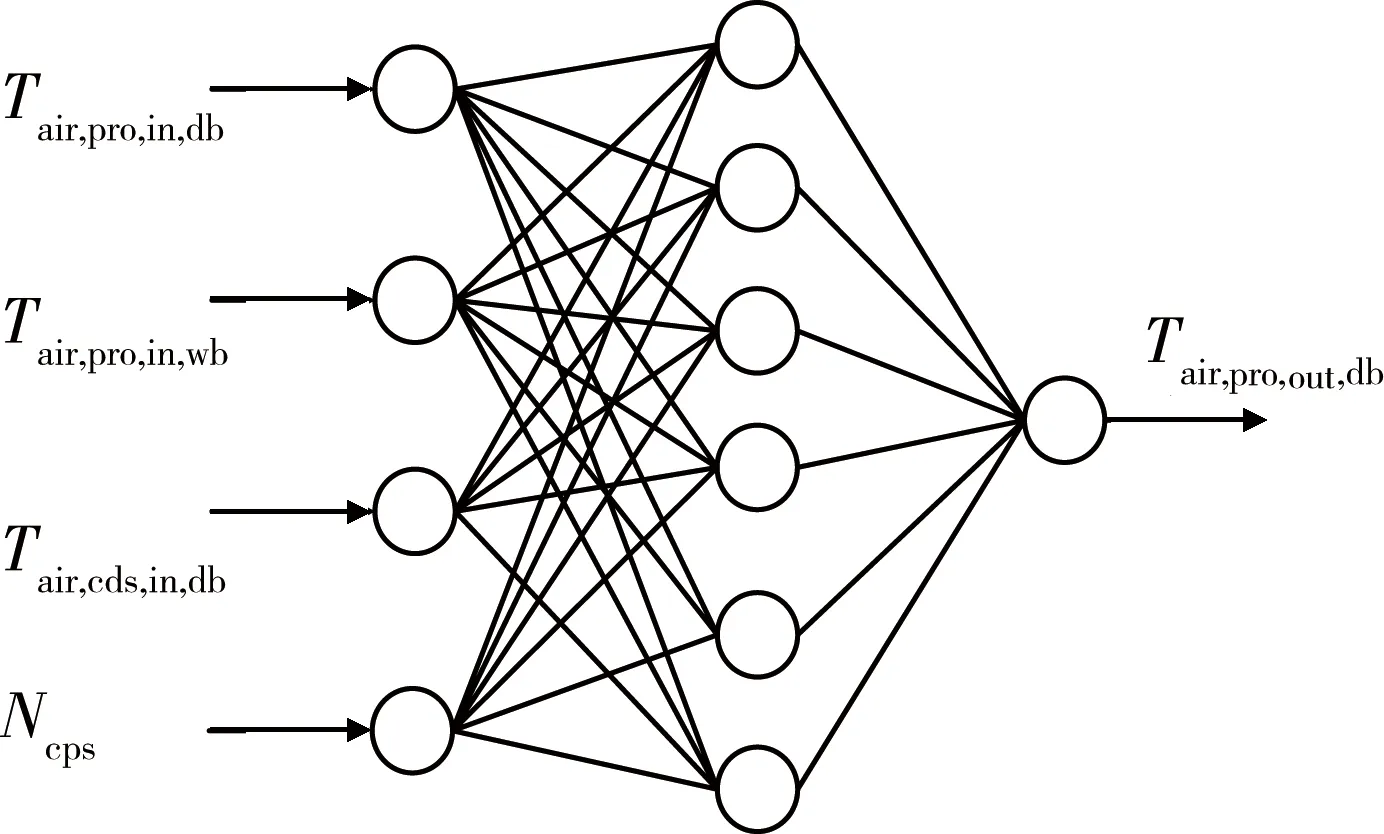
圖2 處理空氣出口干球溫度網絡模型結構

為保證神經網絡完全求解，當網絡輸入個數Nin、輸出個數Nout和訓練數據個數Ntrain確定后，神經元數量Nn需滿足

Ntrain≥(Nin+Nout+1)×Nn+Nout。

(1)

由于Nin=4，Nout=1，Ntrain=40，由式(1)可確定神經元數量Nn=6，此時訓練數據最少為37個，給定的40個訓練數據滿足要求。

3)訓練算法的確定。為減小模型陷入過擬合的概率，采取了以下措施：(1)將實驗數據分為訓練樣本、驗證樣本和觀察樣本，其中，訓練樣本用于訓練網絡，驗證樣本用于計算每次迭代得到的均方誤差(Mean Square Error, MSE)，當該值連續多次大于得到的最低MSE值時，算法結束，觀察樣本僅用于再次檢驗模型精度，其對模型訓練過程不產生影響；(2)當梯度值小于設定值時，說明誤差降低速度非常慢，繼續優化已失去意義，可終止算法。

在神經網絡的訓練算法中，具有代表性的有梯度法、牛頓法和Levenberg-Marquardt(LM)法，其中：最速下降法(Steepest Descent, SD)是一種典型的梯度訓練算法，它采用速率固定的速度搜索模型參數；牛頓法具有非常快的收斂速度，但需要計算誤差性能函數對網絡參數的二階導數(即Hessian矩陣)，計算量和存儲要求都很大，應用較少[11]；而LM法引入了JTJ(J為Jacobian 矩陣)和調整因子μ，實現了牛頓法和變學習速度梯度法的融合。需要說明的是，雖然JTJ與Hessian矩陣表達式類似，但前者僅是誤差和對參數的一階導數，運算量小存儲要求較低。

3 訓練結果

分別用SD法和LM法對上文所建的網絡模型進行尋優，利用MATLAB工具箱編寫代碼，2種算法的尋優參數設置如表2所示。

表2 2種算法的尋優參數設置

2種算法的尋優過程分別如圖3、4所示。由圖3可見：LM法具有非常快的收斂速度，MSE值下降速度非常快，第6次迭代得到的最優驗證MSE值為0.010624；之后，雖然訓練MSE值在降低，但驗證MSE值一直大于此前尋優的最小值，當迭代到第12次時，驗證MSE值連續6次大于最小值，尋優結束。

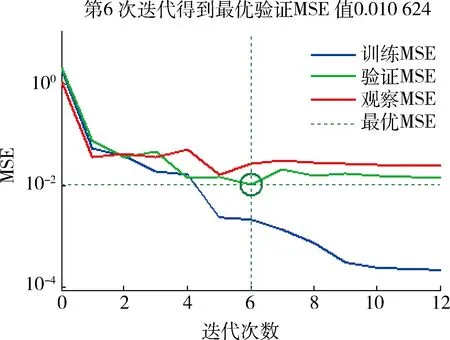
圖3 LM法的尋優過程

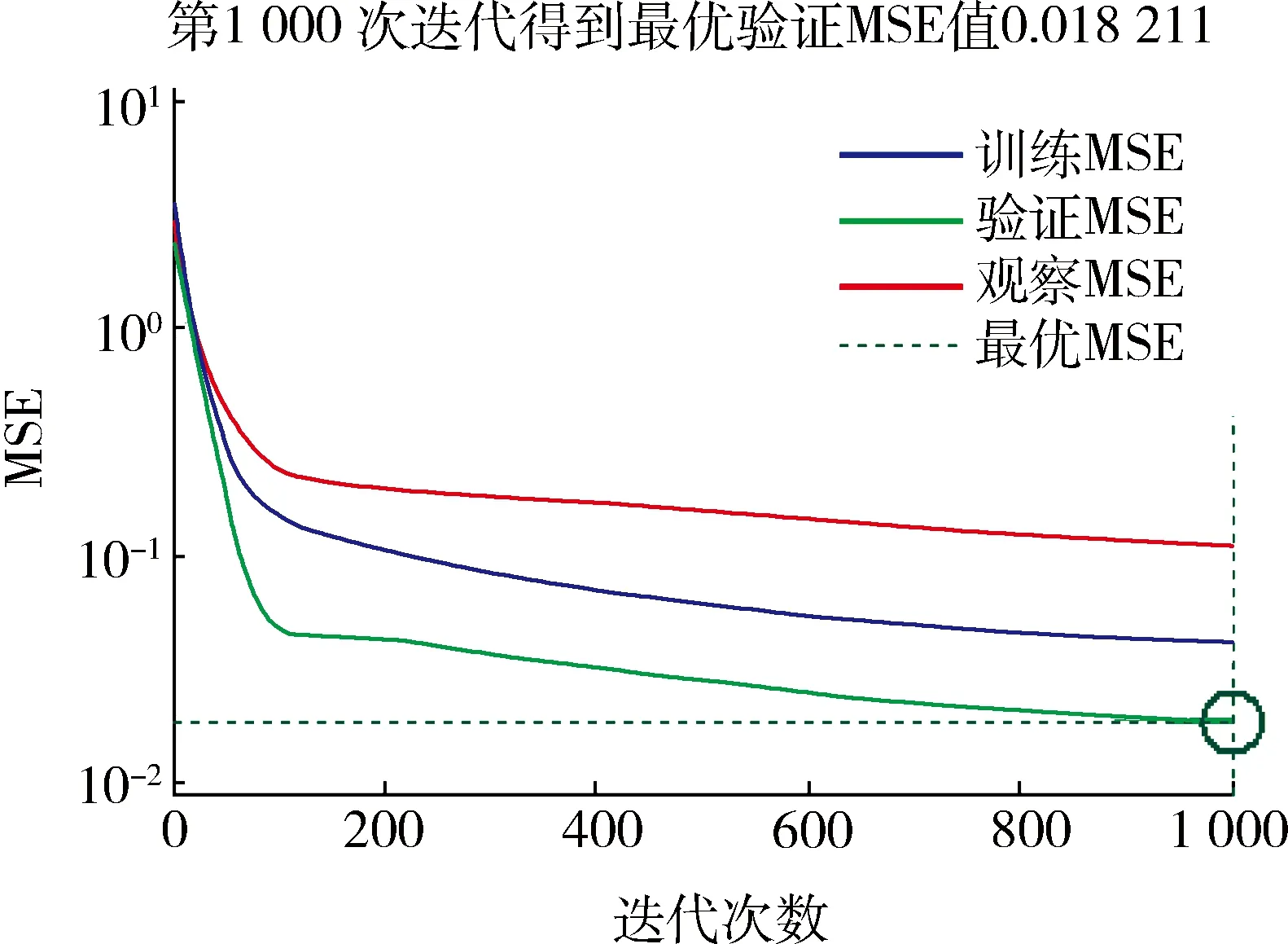
圖4 SD法的尋優過程

由圖4可見：SD法需要1 000次迭代完成尋優，與LM法相比，整個過程訓練MSE值和驗證MSE值下降速度均非常慢，當迭代到第1 000次時得到的最優驗證MSE值為0.018 211，大于LM法得到的最優驗證MSE值，說明了SD法尋優能力低于LM法。需要說明的是:圖3、4中的MSE值為訓練數據經過歸一化處理后得到的值，并非原數據的MSE值。

表3為2種訓練算法的精度對比，可以看出：LM法訓練的平均絕對誤差(Mean Absolute Error, MAE)和MSE值均比SD法小一個數量級，且其模型輸出與實際輸出的相關度R也比SD法更接近1，說明LM法尋優能力更強。這主要是由于LM法采用了牛頓法和可變學習速度法相結合的尋優策略，在不同的尋優階段通過調整μ值實現了不同的尋優速度，大大提高了尋優效率。

表3 2種訓練算法的精度對比

4 制冷系統網絡模型的應用

當工況已知時，可應用所建網絡模型預測處理空氣出口狀態，為制冷系統的優化設計和高精度控制提供參考。

筆者基于LM法所建立的神經網絡模型，選擇1.2節所預留的20組預測數據對處理空氣出口干球溫度進行預測，并將預測結果與實際結果進行對比，如圖5所示。可以看出：預測輸出能很好地跟蹤期望輸出，二者的誤差基本保持在5%以內。表4為基于LM法的神經網絡預測精度，可見：MSE值和MAE值均在較小的范圍內，R值非常接近1，模型預測效果非常好。

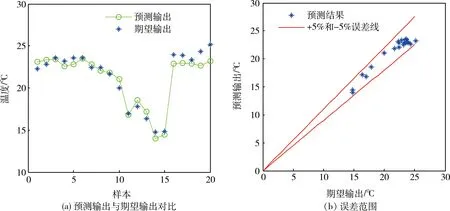
圖5 處理空氣出口干球溫度預測結果

表4 基于LM法的神經網絡預測精度

5 結論

筆者對基于神經網絡的制冷系統建模方法進行了研究，對建模過程中涉及的各要素進行了分析，將基于LM法所建立的神經網絡模型應用于處理空氣出口干球溫度的預測，得到了高精度的預測結果，說明建模方法有效。此外，建模過程中使用了不多的訓練樣本(40個)就獲得了高精度模型，說明系統內部存在弱線性。

[1] Yang Y L, Jiang P C, Cong H, et al. Research on the Route Optimization for Fresh Air Processing of Air Handling Unit in Spacecraft Launching Site[J]. Applied Thermal Engineering, 2015,86(5): 292-300.

[2] 王美霞.小型變頻空調系統動態特性及控制策略研究[D].南京:東南大學, 2005.

[3] Mohanraj M, Jayaraj S, Muraleedharan C. Applications of Artificial Neural Networks for Refrigeration, Air-conditioning and Heat Pump Systems：A Review[J]. Renewable and Sustainable Energy Reviews, 2012, 16(2): 1340-1358.

[4] 趙永標. 基于人工神經網絡的制冷空調系統的仿真研究[D]. 武漢:武漢理工大學, 2005.

[5] Pérez C. Thermodynamic Properties of Refrigerants Using Artificial Neural Networks [J]. International Journal of Refrigeration, 2014, 46: 9-16.

[6] Hosoz M H, Ertunc M. Modeling of a Cascade Refrigeration System Using Artificial Neural Networks [J]. International Journal of Energy Research, 2006, 30(14):1200-1215.

[7] Li N, Xia L, Deng S M, et al. Dynamic Modeling and Control of a Direct Expansion Air Conditioning System Using Artificial Neural Network [J]. Applied Energy, 2012, 91: 290-300.

[8] Ng B C, Darus I Z M, Jamaluddin H, et al. Dynamic Modelling of an Automotive Variable Speed Air Conditioning System Using Nonlinear Autoregressive Exogenous Neural Networks [J]. App-lied Thermal Engineering, 2014, 73: 1255-1269.

[9] Tian Z, Gu B, Qian C, et al. Electronic Expansion Valve Mass Flow Rate Prediction Based on Dimensionless Correlation and ANN Model [J]. International Journal of Refrigeration, 2015, 57: 1-10.

[10] 趙靈曉.基于部件神經網絡模型的制冷系統混合仿真方法及應用[D].上海：上海交通大學, 2010.

[11] Hagan M T, Howard B D. Neural Network Design [M]. Beijing: China Machine Press, 2005：12-19.

(責任編輯: 尚彩娟)

Modeling Method of Vapor Compression Refrigeration System Based on Artificial Neural Network

YANG Yong-li1, CONG Hua2, JIANG Peng-cheng1, FENG Fu-zhou1

(1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2. Department of Science Research, Academy of Armored Force Engineering, Beijing 100072, China)

Aiming at the problems that the traditional modeling method of Vapor Compression Refrigeration System (VCRS) has a large amount of computation and the accuracy of modeling is difficult to guarantee, the modeling method based on Artificial Neural Network (ANN) is researched. Combined with the practical characteristics of VCRS, the training data and network structure are studied and determined, and the network training algorithm is analyzed. By using Levenberg-Marquardt (LM) method and the steepest descent method, 2 typical network training algorithms are used to optimize the parameters of neural network, and the advantages and disadvantages of the 2 algorithms are compared. Finally, the network model is applied to the prediction of the output variables of VCRS. The results show that the network model has higher prediction accuracy, and the modeling method is effective.

Vapor Compression Refrigeration System (VCRS) ; Artificial Neural Network (ANN); modeling; steepest descent method; Levenberg-Marquardt (LM) method

1672-1497(2016)05-0069-04

2016-08-01

軍隊科研計劃項目

楊永利(1988-)，男，博士研究生。

TP183; TB657.2

A

10.3969/j.issn.1672-1497.2016.05.014