關于求直線斜率方法的探討

◆金玉國

(遼寧省阜新市第一中等職業技術專業學校)

關于求直線斜率方法的探討

◆金玉國

(遼寧省阜新市第一中等職業技術專業學校)

在解析幾何中直線方程的確定是十分重要的，而斜率又是確定直線方程的關鍵。結合教學經驗，總結了關于求直線斜率方法的問題。

直線斜率 定義法 公式法 斜截式 向量 導數 點差法 待定系數法

在解析幾何中，直線方程的確定是十分重要的，而斜率又是確定直線方程的關鍵。下面結合筆者多年的教學經驗，總結一下關于求直線斜率方法的問題。

一、定義法：利用定義k=tanα(α≠900)求斜率

例1.如圖正三角形OAB求兩邊OA、OB所在直線的斜率。

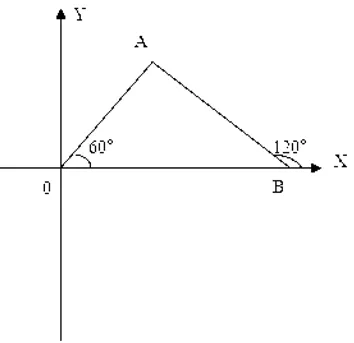
解：∵在正三角形中∠AOB=600∠ABO=600

∴直線AO的傾斜角為600AB的傾斜角為1200

點評：此類問題的解答關鍵是確定直線與x軸的位置關系。

二、利用公式法

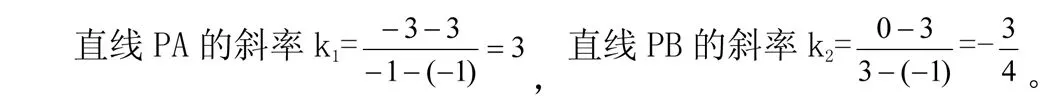
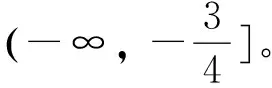
點評：直線經過的兩點不分先后順序，只要坐標保持一致即可。求斜率時要注意斜率不存在的情況。

三、利用直線方程的斜截式求斜率

四、利用向量求斜率

五、利用導數求切線的斜率

在求過曲線上一點(x0,y0)切線的斜率時，先對曲線方程求導，得到導函數，然后把x=x0帶入導函數方程，得到的y，的值就是所求切線的斜率。

例7.求過曲線y=2x3+x-3上的點(2,15)的切線的斜率。

解：對y=2x3+x-3求導得：y，=6x2+1，把x=2代入上式得y，=25，

所求直線斜率為k=25。

六、待定系數法求直線斜率

點評：注意根據上面算法如果得出k不存在時，不要下結論所求直線不存在，而是此直線斜率不存在，但直線是存在的寫成x=x0(x0為所過的點的橫坐標)

七、利用兩直線特殊關系求斜率

若兩條直線平行，它們的斜率相同；若兩條直線垂直，它們的斜率互為負倒數。

例9.求過點A(1，2)且與直線3x-4y+8=0①平行的直線方程，②垂直的直線方程。

九、利用“點差法”求直線斜率

在解有關以圓錐曲線某定點為中點的弦所在的直線方程的問題時，可以用“點差法”求直線斜率。

點評：利用“點差法”求直線斜率有時會產生增根，要注意檢驗。

[1]李小紅.在中職數學中直線斜率求法的探析[J].新課程學習，2012，(10).

[2]吳茂慶.數學[M].南京：江蘇教育出版社，2006.

[3]王文秀.數學復習用書[M].北京：原子能出版社，2008.