遺傳算法與蟻群算法在海洋調查路徑規劃中的應用

張寒野，凌建忠

（中國水產科學研究院東海水產研究所，農業部東海與遠洋漁業資源開發利用重點實驗室，上海 200090）

遺傳算法與蟻群算法在海洋調查路徑規劃中的應用

張寒野，凌建忠

（中國水產科學研究院東海水產研究所，農業部東海與遠洋漁業資源開發利用重點實驗室，上海 200090）

分別以遺傳算法與蟻群算法對23個站位的海洋漁業資源調查路徑進行規劃，尋找其最優路徑。求解結果表明，遺傳算法和蟻群算法都能找到同樣的最短路徑，比實際路徑縮短了8.32%的里程。蟻群算法求得的平均路徑長度小于遺傳算法，但所耗時間比遺傳算法多一倍左右。

路徑規劃；遺傳算法；蟻群算法；海洋漁業；資源調查

我國擁有廣袤的海洋面積，蘊藏著豐富的生物、能源和礦產資源。為了掌握海域資源環境現狀，我國于1996年開始了專屬經濟區和大陸架勘測工作［1］，陸續開展了各種海洋資源與環境調查。海洋調查中常用的方法是派出調查船，沿預先設計的航線逐點采樣觀測。這是項耗資費時的工作，科學地規劃調查路徑對于提高調查效率、降低成本具有重要意義。

尋找最優路徑是一類組合優化問題，實際上是一個旅行商問題（travelling salesman problem，TSP），TSP已被證明是一個多項式復雜程度的非確定性（non-deterministic polynomial，NP）問題，即沒有確定的算法能在多項式時間內得到問題的解。如果用精確算法求解，隨著節點數目的增加，可能的路徑數目呈指數增長，難以解決大規模問題。因此一般采用遺傳算法、蟻群算法等啟發式算法，求得近似解滿足要求。

遺傳算法（genetic algorithm，GA）［2］是模擬自然界生物進化中遺傳、突變、雜交和適者生存等現象，從一定數量的初始解開始，經過一系列進化，逐步逼近問題的最優解的一種算法。蟻群算法（ant colony optimization，ACO）［3－4］也是一種仿生算法，是模擬螞蟻在搜索食物時尋找最優路徑的過程而得到的算法：螞蟻在覓食過程中會在經過的路徑上留下一種信息素，并且信息素的濃度與路徑長度成反比，經過同一路徑的螞蟻越多，該路徑上的信息素濃度就越高，吸引后來的螞蟻選擇該路徑的概率也越大，最終使整個蟻群趨于最優路徑上。這類仿生算法已廣泛應用于組合優化領域［5－8］。本文將遺傳算法和蟻群算法應用于海洋漁業資源調查，比較兩者的優劣，以期實現海洋調查最優化路徑的分析和求解。

1 材料與方法

1.1 遺傳算法

1.1.1 編碼方式

0表示出發和返回位置，1，2，…n表示n個調查站位，以站位的遍歷次序作為遺傳算法的編碼。一個編碼是一個個體，代表一個可行解，即一條路徑。隨機產生N個編碼，組成初始種群。

1.1.2 適應度函數

適應度函數是用于評價種群中每個個體路徑優劣的指標，適應度值越大，該個體被遺傳到下一代的概率也越大。路徑越短說明這個解越好，其適應度也越大，因此可將適應度函數取為路徑長度的倒數。

1.1.3 選擇操作

選擇的方式采用輪盤賭法，每個個體被選中遺傳到下一代的概率與其在群體中的相對適應度成正比。此外還采用了精英保留策略，每一代適應度最高的個體原樣遺傳到下一代，以保證最優者生存下來。

1.1.4 變異操作與交叉操作

將被選擇遺傳到下一代的個體，按預先設定的概率進行變異和交叉操作，改變局部編碼，生成新個體。變異操作是隨機選擇路徑上的兩個點交換位置，從而產生一個新個體。交叉操作是選擇兩個父代個體，隨機選擇兩個交叉點，并互換這兩個交叉點之間的編碼，為保證每個站位都遍歷一次且僅有一次，互換后將交叉點以外的部分中與交叉點之間重復的站位用另一個父代的相應位置代替，這樣形成兩個新個體。

1.1.5 進化中止

當適應度達到期望的結果或迭代超過預設的次數，則進化中止。

1.1.6 參數設置

遺傳算法運行時所使用的參數如表1所示。

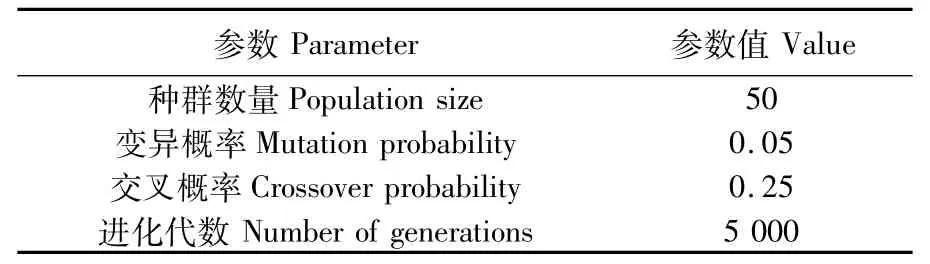
表1 遺傳算法的參數設置Tab.1 Parameters of GA

1.2 蟻群算法

1.2.1 選擇概率［9］

t時刻時，位于站位i的螞蟻k選擇向下一個站位j移動的概率為：

式中，τij（t）表示t時刻從i站位到j站位路徑上信息素的濃度，dij表示站位i和j之間的距離，α表示信息素濃度的相對重要性，β表示站位間距離的相對重要性，allowedk表示允許螞蟻k下一步選擇的站位的集合。

1.2.2 信息素更新

初始狀態下信息素濃度設為1。當所有螞蟻完成一次遍歷后，對路徑上的信息素濃度進行更新，t＋1時刻從i站位到j站位路徑上信息素的濃度為：

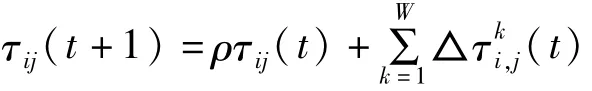
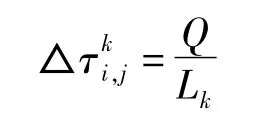
式中，Q為每只螞蟻能釋放的信息素總量，是一個常數，Lk表示螞蟻k在本次遍歷經過路徑的總長度。

1.2.3 參數設置

蟻群算法運行時所使用的參數如表2所示。

表2 蟻群算法的參數設置Tab.2 Parameters of ACO

1.3 路徑距離計算

假設地球是完美的球體，任意兩個調查站位i和j經度分別為λi和λj，緯度分別為φi和φj，則兩個站位間的距離為：

式中，R為地球半徑。

1.4 調查站位

以2014年5月東海北部的一次漁業資源調查為例，分別以遺傳算法和蟻群算法進行調查路徑規劃，此次調查共有23個站位，分布如圖1所示。

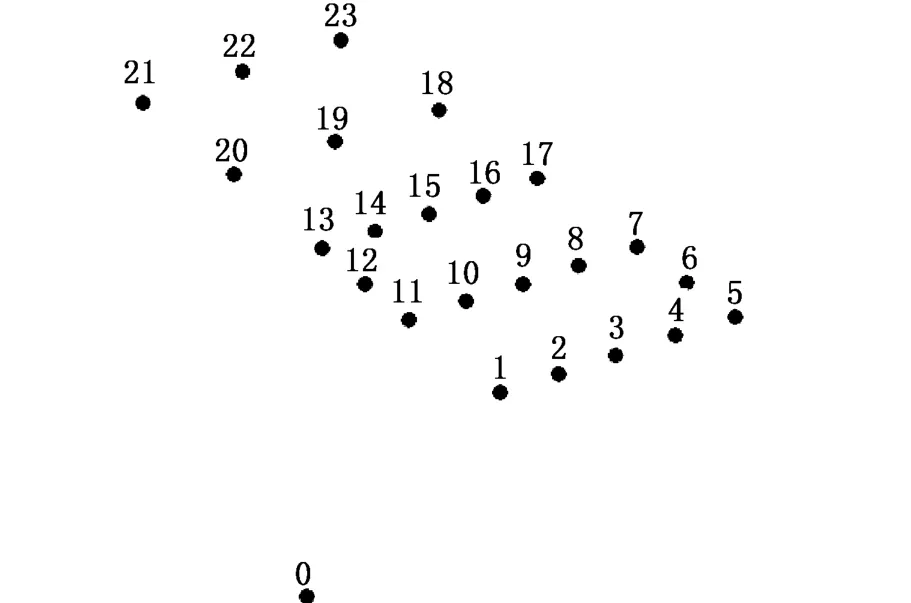
圖1 站位分布圖Fig.1 Distribution of survey stations

表3 兩種算法結果對比Tab.3 Com parison of results between GA and ACA

2 結果與分析

用遺傳算法和蟻群算法分別進行100次路徑規劃運算，其結果如表3所示。由表3可見，遺傳算法和蟻群算法都能找到同樣的最短路徑；蟻群算法求得的平均路徑長度小于遺傳算法，并且解的分布也比較集中；但是蟻群算法計算過程較復雜，運行所需時間比遺傳算法多一倍左右。

兩種算法所找到的最優路徑如圖2所示，圖3是調查船實際航行軌跡，最優路徑比實際路徑縮短了8.32%的里程。

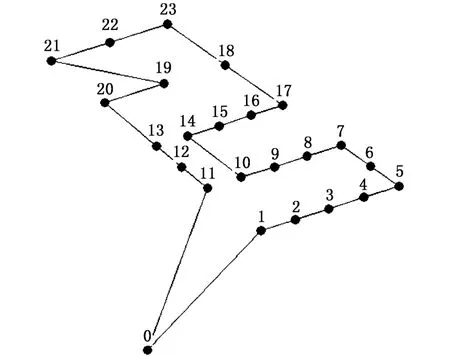
圖2 最優路徑Fig.2 Optimal path

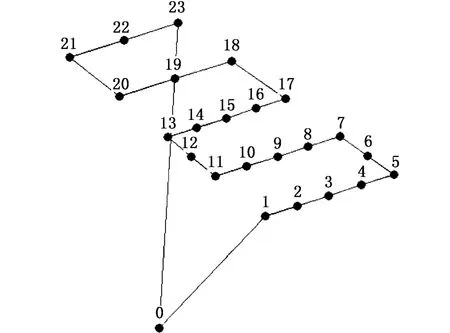
圖3 實際路徑Fig.3 Actual path

圖4是遺傳算法的收斂曲線，從中可以看到其迭代過程，遺傳算法在初始階段收斂較快，隨后進入平穩階段，進化5 000代后，其平均值已接近最優解。

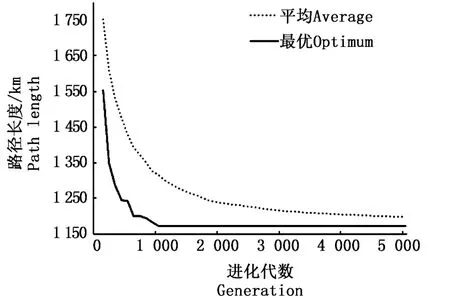
圖4 遺傳算法收斂曲線Fig.4 Convergent curve of GA

圖5是蟻群算法的迭代曲線，也是進行100次運算后統計所得。蟻群算法收斂速度非常快，在運行初期就已經接近最優解。

圖5 蟻群算法的迭代曲線Fig.5 Iterative curve of ACO

運算結果表明，蟻群算法在求解最優路徑時具有較快的收斂性，適用于較精確的求解。遺傳算法運行速度較快，適用于快速求解并且對結果準確度要求不高的場合。

3 討論

遺傳算法與蟻群算法通過不斷迭代，使所要解決的問題從初始解逐漸向最優解逼近。但是最終求得的解可能是次優解，不一定是全局最優解。特別是針對大規模問題，即站位點比較多時，容易陷入早熟和難以跳出局部最優的狀態，出現搜索停滯的現象。不少研究提出了改進方法，如最大最小蟻群系統（max-min ant system，MMAS）［10］修改了蟻群算法中信息素的更新方式，每次迭代后路徑上的信息素濃度被限制在［min，max］范圍內，可以改善算法的停滯現象。也有研究將蟻群算法和遺傳算法相結合［11］，以蟻群算法的解作為遺傳算法的初始種群，加快算法的收斂速度。另外在每次迭代過程中，引入2-opt等局部搜索算法可進一步改善解的質量。

遺傳算法和蟻群算法的參數設定對算法的性能優劣頗為重要。群體規模影響到算法的性能和效率，群體過小則由于搜索空間較小而效果不佳，群體過大則計算量較大導致速度變慢。遺傳算法中變異概率和交叉概率影響著種群的更新速度，概率過高則更新過于頻繁而使算法變成隨機搜索，概率過低則子代和父代過于相似而使進化停滯。蟻群算法中α值越大，螞蟻選擇以前經過路徑的概率也越大；β值越大，選擇局部最短路徑的可能性也越大；ρ值從大到小變化，其算法的隨機性和全局搜索能力變弱，但是能提高收斂速度。遺傳算法和蟻群算法的參數選擇雖然比較重要，但尚沒有數學解析方法求得最優值，在實際應用中一般采用經驗值。

遺傳算法和蟻群算法不僅可用于求解單目標優化問題，也適合求解多目標優化問題［12－15］。應用于海洋調查路徑規劃，除了可以求解單船最短路徑，也可求解多條船同時調查情況下，總成本最低或總路徑最短，且各船經過站位盡可能均衡的問題。對于多目標優化問題，往往不存在滿足所有條件的全局最優解，通常是得到一組Pareto最優解。

［1］ 鄭元甲，陳雪忠，程家驊，等.東海大陸架生物資源與環境［M］.上海：科技出版社，2003.

ZHENG Y J，CHEN X Z，CHENG J H，et al.Biological resources and the environment of East China Sea continental shelf［M］.Shanghai：Shanghai Science and Technology Press，2003.

［2］ HOLLAND JH.Adaptation in natural and artificial systems［M］.Ann Arbor：University of Michigan Press，1975.

［3］ DORIGO M，MANIEZZO V，COLORNIA.The ant system：Optimization by a colony of cooperating agents［J］.IEEE Transactions on System，1996，26（1）：28－41.

［4］ DORIGO M，GAMBARDELLA L M.Ant colonies for traveling salesman problem［J］.BioSystems，1997，43（2）：73－81.

［5］ DORIGO M，CAMBARDELLA L M.Ant colony system：a cooperative learning approach to the traveling salesman problem［J］.IEEE Transactions on Evolutionary Computation，1997，1（1）：53－66.

［6］ COSTA D，HERTZ A.Ants can color graphs［J］.Journal of the Operational Research Society，1997，48（3）：295－305.

［7］ MANIEZZO V，COLORNIA.An ants heuristic for the frequency assignment problem［J］.Future Generation Computer Systems，2000，16（8）：927－935.

［8］ COLORNIA，DORIGOM，MANIEZZO V，et al.Ant system for job shop scheduling［J］.Operations Research，1994，34（1）：39－53.

［9］ MULLEN R J，MONEKOSSO D，BARMAN S，et al.A review of ant algorithms［J］.Expert Systems with Application，2009，36（6）：9608－9617.

［10］ STUTZLE T，HOOS H.Max-min ant system［J］.Future Generation Computer System，2000，16（8）：889－914.

［11］ LEE Z J，SU S F，CHUANG C C，et al.Genetic algorithm with ant colony optimization（GA-ACO）for multiple sequence alignment［J］.Applied Soft Computing，2008，8（1）：55－78.

［12］ KOH S P，ARIS I B，HO C K，et al.Design and performance optimization of a multi-TSP（traveling salesman problem）algorithm［J］.AIML Journal，2006，6（3）：29－33.

［13］ SINGH A，BAGHEL A S.A new grouping genetic algorithm approach to the multiple traveling salesperson problem［J］.Soft Computing-A Fusion of Foundations，Methodologies and Applications，2009，13（1）：95－101.

［14］ CARTER A E，RAGSDALEC T.A new approach to solving the multiple traveling salesperson problemusing genetic algorithms［J］.European Journal of Operational Research，2006，175（1）：246－257.

［15］ GHAFURIAN S，JAVADIAN N.An ant colony algorithm for solving fixed destination multi-depot multiple traveling salesmen problems［J］.Applied Soft Computing，2011，11（1）：1256－1262.

Research of genetic algorithm and ant colony optim ization on path p lanning for oceanography survey

ZHANG Han-ye，LING Jian-zhong
（Key Laboratory of East China Sea＆Oceanic Fishery Resources Exploitation and Utilization，Ministry of Agriculture，East China Sea Fisheries Institute，Chinese Academy of Fishery Sciences，Shanghai200090，China）

Searching for the optimal path is one of the most important combinatorial optimization problems.Since this problem belongs to NP-hard problems，an exact algorithm could not solve the large-scale problems in time，somemetaheuristic approaches have been used to solve it in recent years.Genetic algorithm works in a way similar to the process of natural evolution，such as inheritance，mutation，selection and crossover.A basic GA starts with a random ly generated population of candidate solutions.After the evolution of several generations，the optimal solution for the problem is obtained.Ant colony optimization algorithm is to mimic themovements of ants.Ants leave a trail of pheromoneswhen they search for food，and the pheromone density becomes higher on shorter paths than longer ones.As more ants use a particular trail，the pheromone concentration on it increases，hence attracting more ants.Consequently，all ants follow a best path.This article presented GA and ACO for solving the path planning of 23 stations for a fishing resource survey.The results indicate that both algorithm are able to find out the same shortest path，which is 8.32%shorter than the actual path.The average path length obtained by ACO is less than thatby GA，but it takes nearly twice as long.It is suggested that ACO has better convergence and more acurate calculation results，as well as GA is suitable for fastsolving and roughly estimating the problems.

path planning；genetic algorithm；ant colony optimization；marine fishery；resources survey

S 932.4

A

1004－2490（2016）01－0083－05

2015－07－10

農業部專項近海資源調查（2014）

張寒野（1974－），男，副研究員，碩士，從事海洋漁業資源研究。E-mail：hy＠eastfishery.ac.cn