不同形狀底凹結(jié)構(gòu)對火炮彈丸飛行阻力影響研究*

陸海波,顓孫世周,孫鳳文,李義文

(南京炮兵學(xué)院,南京 211132)

不同形狀底凹結(jié)構(gòu)對火炮彈丸飛行阻力影響研究*

陸海波,顓孫世周,孫鳳文,李義文

(南京炮兵學(xué)院,南京 211132)

文中以改善火炮底凹彈的飛行阻力為目標(biāo),針對火炮彈丸不同底凹結(jié)構(gòu)對減阻效果的影響展開研究。通過基于N-S方程的數(shù)值模擬,得到帶底凹結(jié)構(gòu)彈丸的繞流流場參數(shù)分布以及彈丸的氣動阻力,討論了相同底凹深度、不同形狀底凹結(jié)構(gòu)對彈丸流場、減阻效果的影響。研究發(fā)現(xiàn),彈丸底部凹腔產(chǎn)生位于凹腔內(nèi)的回流流動對底凹結(jié)構(gòu)的減阻效果起決定性作用。研究的三種凹腔形狀中,“收縮”形狀的底凹結(jié)構(gòu)有最小的氣動阻力。

底凹彈;凹腔形狀;減阻;數(shù)值模擬

0 引言

以減小彈丸氣動阻力為手段的火炮增程方法因其不涉及彈丸、發(fā)射藥裝藥量的改變而受到普遍重視。在彈丸飛行過程中,火炮彈丸的氣動阻力主要由彈丸頭部脫體激波產(chǎn)生的波阻、底部流動形成的底阻和彈丸外壁與空氣摩擦產(chǎn)生的摩擦阻力三者構(gòu)成。

減小彈丸飛行時的空氣阻力,對改善彈丸的彈道性能(包括增大射程、飛行速度以及縮短飛行時間等)是十分有利的[1]。底凹結(jié)構(gòu)是一種有效的削弱彈丸底阻的方法[2-3]。在超聲速條件下,彈丸底阻約占總阻的20%～40%[4],通過加入底凹結(jié)構(gòu),可以有效的減弱彈丸的底阻,提高彈丸的射程。此外,底凹結(jié)構(gòu)還對火炮的威力和精度的提高有益。據(jù)設(shè)計實驗表明,在相同條件下,底凹彈可增程3%～5%,如果進(jìn)一步在底部開側(cè)向孔,可增程10%～12%[5]。

彈丸底凹技術(shù)已經(jīng)是一種成熟的彈丸減阻增程技術(shù),但是對于底凹結(jié)構(gòu)本身的分析卻并不多見。文中針對火炮彈丸的底凹結(jié)構(gòu),基于底凹彈繞流流場的數(shù)值仿真,分析了底凹結(jié)構(gòu)減阻效果的形成機理,探討了不同底凹結(jié)構(gòu)對彈丸減阻效果的影響,為底凹結(jié)構(gòu)的優(yōu)化設(shè)計提供理論基礎(chǔ)。

1 結(jié)構(gòu)示意

為了討論不同的底凹結(jié)構(gòu)對彈丸阻力的影響,文中設(shè)置了三種外形的底凹結(jié)構(gòu),圖1給出了結(jié)構(gòu)示意,三種彈丸的外形差異僅存在于底凹結(jié)構(gòu)的不同。底凹結(jié)構(gòu)的擴(kuò)張或者收縮角α為10°

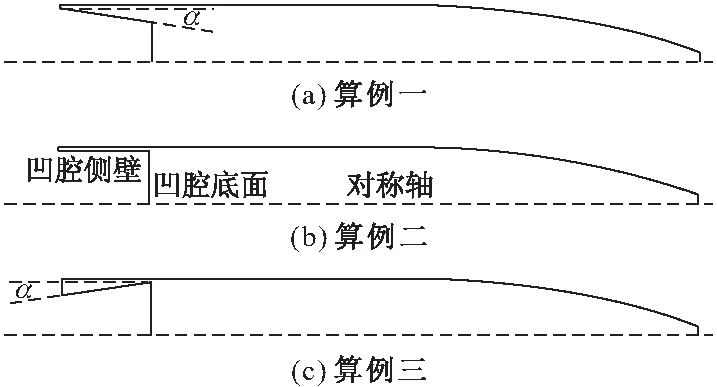
圖1 算例結(jié)構(gòu)示意

2 數(shù)值方法

2.1 控制方程及其離散

基于火炮彈丸超聲速繞流流場的可壓軸對稱特性,基本控制方程選擇了可壓縮的軸對稱N-S方程[6],如式(1)所示。

(1)

式中:x為流向;r為徑向;U為守恒變量;E、F為對流項;Ev、Fv為黏性項;S、H為對應(yīng)的源項。結(jié)合k-ε湍流模型[7]進(jìn)行方程求解。對流通量采用Van Leer格式處理,黏性擴(kuò)散項采用2階中心差分格式,時間項采用LU-SSOR的隱式格式離散分解。

2.2 計算網(wǎng)格與邊界條件

數(shù)值計算中使用的貼體計算網(wǎng)格如圖2所示(算例三為例)。

圖2 計算網(wǎng)格(算例三)

數(shù)值仿真中忽略彈丸自旋對流場的影響。彈丸壁面無滑移并且使用了絕熱壁假設(shè)。流動邊界條件如表1所示。

表1 流動邊界條件

3 結(jié)果與分析

3.1 流場參數(shù)分布

圖3～圖5分別給出了各算例超聲速繞流流場的流線和馬赫數(shù)、溫度以及壓力分布情況。基于超聲速流動后方擾動無法向前傳遞的特性,底凹結(jié)構(gòu)的影響主要體現(xiàn)于彈丸的尾部流場,計算結(jié)果也體現(xiàn)了這一特性。

圖3為各算例流場流線及馬赫數(shù)分布。由圖可知,超聲速來流與彈丸頭部相遇,產(chǎn)生繞彈丸頂端(引信部分)的脫體弓形激波,來流經(jīng)激波減速,但波后的流速依然沒有跌入亞聲速,繞流沿彈丸頭部進(jìn)入圓柱部,繞流發(fā)生一次膨脹,由計算結(jié)果亦可見,彈丸圓柱部外存在繞流的加速。繞流至彈丸尾部時,流動急劇擴(kuò)張又形成了一個高速膨脹區(qū),彈丸繞流流場的最大流速即在此區(qū)域產(chǎn)生。在彈丸的底部,由于底凹結(jié)構(gòu)的存在,沿底凹形成了顯著的回流區(qū)域。

圖4以算例三為例給出了底凹彈繞流流場的溫度云圖。事實上各算例繞流流場的溫度分布都體現(xiàn)了激波后升溫、膨脹區(qū)域降溫、回流區(qū)域高溫的經(jīng)典彈丸繞流溫度分布。

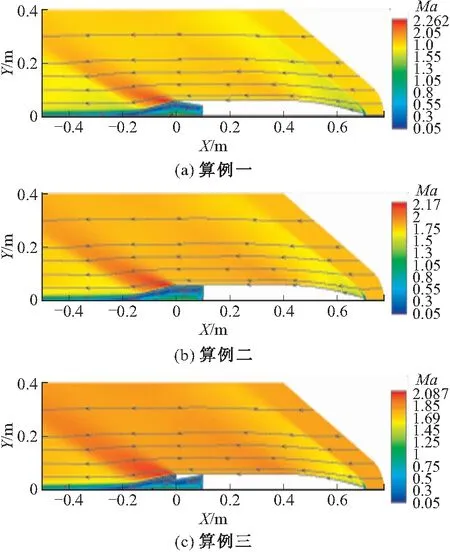
圖3 各底凹結(jié)構(gòu)彈丸Ma及流線分布

圖4 算例三底凹結(jié)構(gòu)彈丸流場溫度分布

圖5為各算例流場壓力等值線分布,由圖可見清晰的激波后高壓,彈丸圓柱部、尾部膨脹低壓。

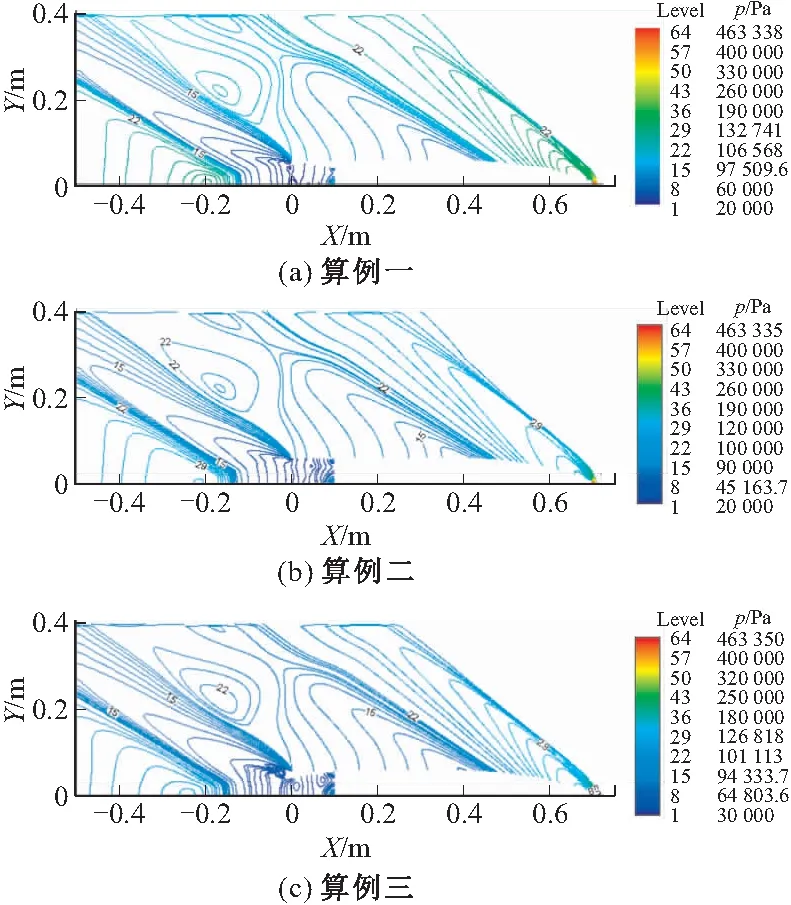
圖5 各底凹結(jié)構(gòu)彈丸壓力分布

圖6以算例三為例,給出了凹腔內(nèi)部的壓力分布放大圖。由圖可見,由于底凹結(jié)構(gòu)的存在,使得底部回流有了“充分發(fā)展”的空間,在底凹結(jié)構(gòu)內(nèi)部彈丸的底面上出現(xiàn)了兩個相對高壓。一個靠近中軸線,一個分布于凹腔的轉(zhuǎn)角。

需要指出的是,對算例三所采取的收縮式底凹結(jié)構(gòu)而言,由于凹腔側(cè)壁的傾斜方向使得彈丸尾部出現(xiàn)了一個有著較大面積的圓環(huán)結(jié)構(gòu)(彈尾底面,圖6中直線MN部分),而彈丸的繞流流動在彈丸尾部轉(zhuǎn)折處(圖6中M點)會發(fā)生急劇膨脹。事實上,仿真結(jié)果也顯示出,緊貼MN確實存在一個局部的低壓區(qū)。對于算例一、二采取的底凹結(jié)構(gòu)而言,此處的長度(實際為圓環(huán)面積)很小。算例三的彈尾底面結(jié)構(gòu)特性會增大彈丸的飛行阻力。

此外,對算例一、三而言,由于凹腔側(cè)壁的傾斜方向不同(圖1),作用于凹腔側(cè)壁上的壓力向彈丸軸向分解,產(chǎn)生的效果也不同。算例一,擴(kuò)張式的凹腔結(jié)構(gòu),側(cè)壁受力的軸向分量與彈丸氣動阻力相反,對彈丸減阻起優(yōu)化作用;算例三,收縮式的凹腔結(jié)構(gòu),側(cè)壁受力的軸向分量與彈丸氣動阻力相同,會增加彈丸的阻力。

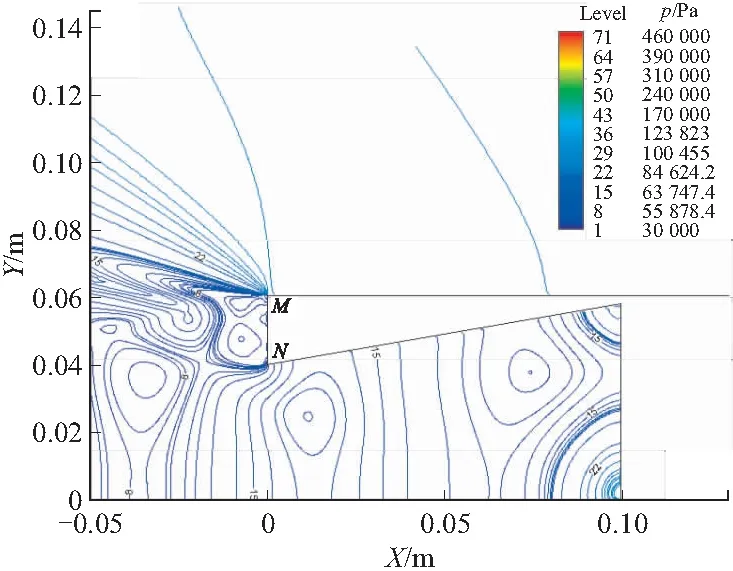
圖6 算例三彈丸底部壓力分布(放大)

3.2 氣動阻力

彈丸氣動阻力系數(shù)Cd計算式如下:

(3)

式中:Fd為氣動阻力;ρ∞為來流密度;u∞為來流速率;Sref為參考面積,取彈丸圓柱部的橫截面積。

表2給出了各算例的氣動阻力系數(shù),由表可見,算例三有最小的氣動阻力,算例一氣動阻力最大,即在文中的模擬條件下,對三種底凹結(jié)構(gòu)而言,收縮式的底凹結(jié)構(gòu)能夠形成最大的彈丸底部壓力,這種結(jié)構(gòu)最有利于彈丸的減阻,而算例一擴(kuò)張式的底凹結(jié)構(gòu)最劣,甚至不如算例二的圓柱式結(jié)構(gòu)。

表2 各算例阻力系數(shù)

表2中氣動力的計算結(jié)果仿佛與前文中結(jié)合圖6對各算例結(jié)構(gòu)特性對彈丸阻力影響的趨勢相左,實則不然。圖7給出了各個算例凹腔底面的壓力分布。由圖可知,算例一的凹腔外形有最好的底面壓力恢復(fù)(這主要取決于直接受凹腔形狀影響的彈尾回流的強弱),沿凹腔底面算例一的兩個局部高壓區(qū)在3個算例中均有最大值。但亦可見,算例一的曲線長度最短,也即擴(kuò)張式的凹腔結(jié)構(gòu)有最小的凹腔底面面積。算例二與算例三,凹腔底面面積相同,但算例三的底面壓力的表現(xiàn)要優(yōu)于算例二。

由如上分析可見,當(dāng)進(jìn)一步考慮各算例凹腔底面的壓力特性之時,算例三的凹腔構(gòu)型是最有利于彈丸減阻的。亦可知,對于底凹結(jié)構(gòu)減阻而言,凹腔底面上的受力特性在結(jié)構(gòu)各處上,占有主導(dǎo)地位。

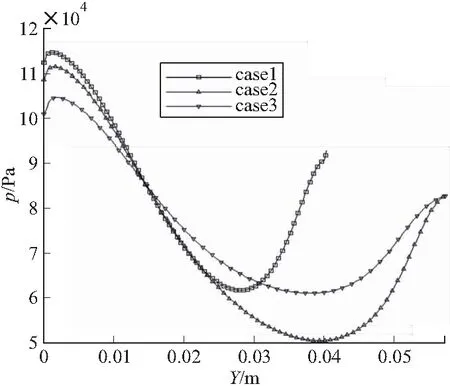
圖7 各算例彈丸凹腔底面壓力分布

4 結(jié)論

文中以數(shù)值模擬為主要研究手段,對火炮旋成體彈丸采取不同底凹結(jié)構(gòu)的減阻效果展開研究。主要結(jié)論如下:

1)合適的底凹結(jié)構(gòu)能夠有效的減小火炮彈丸的氣動阻力。

2)在文中計算條件下,彈丸底部凹腔采用收縮式的結(jié)構(gòu),彈丸的飛行阻力最小;擴(kuò)張式結(jié)構(gòu)的彈丸阻力最大。

3)彈丸底部的回流流動對底凹結(jié)構(gòu)的減阻效果有重要影響。

4)凹腔底面的受力情況在凹腔結(jié)構(gòu)對彈丸減阻的影響中,占有主導(dǎo)地位。

[1] 王中原. 超聲速底凹彈側(cè)壁開孔對飛行阻力的影響 [J]. 空氣動力學(xué)學(xué)報, 1997, 15(4): 502-506.

[2] HOWELL J, SIMS-WILLIAMS D, SPROT A, et al. Bluff body drag reduction with ventilated base cavities [J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2012, 5(1): 152-160.

[3] IBRAHIM A, FILIPPONE A. Supersonic aerodynamics of a projectile with slot cavities [J]. Aeronautical Journal, 2010, 113(1150): 15-24.

[4] 浦發(fā), 王中原. 減阻增程的潛力及其可能途徑的分析 [J]. 彈道學(xué)報, 1986(3): 38-42.

[5] 華恭, 歐林爾. 彈丸作用和設(shè)計理論 [M]. 北京: 國防工業(yè)出版社, 1975: 58.

[6] 王承堯, 王正華, 楊曉輝. 計算流體力學(xué)及其并行算法 [M]. 長沙: 國防科大出版社, 2000: 4.

[7] 陶文銓. 數(shù)值傳熱學(xué) [M]. 2版. 西安: 西安交通大學(xué)出版社, 2001: 152.

Research on Influence of Base Cavity with Different Shape on Aerodynamic Drag of Projectile

LU Haibo,ZHUANSUN Shizhou,SUN Fengwen,LI Yiwen

(Nanjing Artillery Academy, Nanjing 211132, China)

In order to improve aerodynamic drag of projectile with base cavity, drag reducing effect got from projectiles with different base cavity was investigated. Based on Navier-Stokes (N-S) equations, distribution of flow field parameters and aerodynamic drag was obtained by numerical simulation method. The effect of base cavity with same length but different shape on flow field and drag reduction were discussed. The results show that the recirculation region, which is caused by the base cavity and located inside the cavity, plays a pivotal role in reduction of the drag. In the paper, the projectile with a “contraction” shape has the minimum aerodynamic drag.

projectile with base cavity; cavity shape; drag reduction; numerical simulation

2015-09-15

陸海波(1980-),男,新疆昌吉人,講師,博士,研究方向:高速飛行器氣動力、熱分析與控制。

TJ012

A