非線性確定采樣型濾波器采樣點優化算法*
吳青坡,叢源材,周紹磊
(1 92313部隊,河南濟源 459000;2 92886部隊,山東膠州 266300;3 海軍航空工程學院,山東煙臺 264001)
非線性確定采樣型濾波器采樣點優化算法*
吳青坡1,3,叢源材2,周紹磊3
(1 92313部隊,河南濟源 459000;2 92886部隊,山東膠州 266300;3 海軍航空工程學院,山東煙臺 264001)
采樣點的選取對確定采樣型濾波器的精度和穩定性起著決定性作用,為提高濾波器的數值穩定性,首先,采用協方差矩陣分解方法對獲得的采樣點進行優化,解決了數值大小對采樣點離采樣中心距離的影響問題;其次,通過選擇合適的正交變換,在不改變濾波精度的前提下消除了采樣點中存在的非局部效應;最后,利用一個落體跟蹤模型對所提基于采樣點優化方法的確定采樣型濾波器進行仿真分析,仿真結果驗證了該采樣點優化方法的有效性。
確定采樣型濾波器;采樣點優化;協方差矩陣分解;正交變換
0 引言
對于線性高斯系統,Kalman濾波即是最優濾波器,而對于非線性系統,人們主要采用擴展Kalman濾波器(extended Kalman filter,EKF)及其相關改進算法等次優解的近似方法。但EKF存在精度偏低、需計算Jacobian矩陣、要求非線性函數連續可微等理論局限性,系統具有強非線性和高維數時數值穩定性較差,濾波精度不佳[1]。確定采樣型濾波因具有實現簡單、估計精度高等優點,目前已得到國內外學者的廣泛關注[2-6]。
確定采樣型濾波器在應用過程中出現濾波發散或失敗的情況,主要是由于在協方差矩陣的計算中出現了非正定的協方差矩陣和非局部效應導致的協方差矩陣過大[7],Julier提出了對采樣點進行比例修正的方法,提供了3個自由參數來調整采樣點到采樣中心的距離和權值,但并沒給出參數調整的具體方法。Merwe[8]提出在濾波過程中采用協方差矩陣的平方根矩陣代替協方差矩陣,然而導致協方差矩陣非正定的因素并沒有消除。Lefebvre[9]提出增加一個權值為1的中心采樣點來增大協方差矩陣從而保證協方差矩陣半正定,但這會大大降低濾波器的精度。Xiong[10]通過人為增大系統噪聲矩陣來增加濾波器的穩定性,保證了協方差矩陣的半正定性,卻以犧牲精度為代價來提高穩定性。Arasaratnam[6]提出基于球面徑向容積法的CKF(cubature Kalman filter),其獲得采樣點的方法為實現高精度的采樣點提供了理論基礎。CKF解決了UKF(unscented Kalman filter)中采樣點權值為負的問題,同時也帶來了非局部效應,限制了其在高維系統中的應用。Chang[11]巧妙地構建了一個正交矩陣,消除了非局部效應。
為提高確定采樣型濾波器的數值穩定性,避免濾波發散,文中從協方差矩陣分解的角度研究了提高濾波器穩定性的方法。采用基于相關系數分解的方法獲得平方根矩陣,可有效消除濾波采樣點中由于協方差矩陣中元素數值大小而產生的遠離采樣中心的問題。利用正交變換方法,在不會改變濾波精度的前提下消除了采樣點中存在的非局部效應。
1 確定采樣型濾波器
給定系統狀態方程和量測方程
xk+1=f(xk)+wk+1
(1)
yk+1=h(xk+1)+vk+1
(2)
式中:xk∈Rn為n維狀態向量;yk∈Rm為m維量測向量;系統噪聲wk和量測噪聲vk均為高斯白噪聲,協方差矩陣分別為Qk和Rk;wk和vk相互獨立,且與狀態量和量測量不相關。
確定采樣型濾波器在非線性高斯濾波框架下通過對一二階矩近似實現狀態估計,過程如下[3-5]:
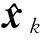
2)狀態傳遞方程
χi=f(σi)
3)量測更新方程
ξi=h(χi)
2 協方差矩陣分解
這里采用基于相關系數矩陣分解的新方法對協方差矩陣進行分解。
2.1 協方差矩陣中的信息提取
方差代表隨機變量相對其數學期望的分散程度,通常當隨機變量的取值離數學期望越遠則出現的概率越小,與之對應的是采樣點離中心點越遠,其權值越小。在確定采樣中,權值相同的基礎采樣點離中心點的距離相同,但經過線性變換后,距離會發生變化,這是造成濾波器誤差的一個重要原因。標準差代表了一個隨機變量偏離其數學期望的平均距離,如果將采樣點看作是等權值的,那么超出標準差越遠的點出現的概率越小。因此,在協方差矩陣分解時,應當盡可能減小這一變化的影響。
由于隨機向量中各分量標準差大小不同,不同分量間協方差的大小無法準確描述相關程度的大小,對協方差進行標準化得到相關系數ρij為:
ρij描述了狀態變量xi和xj之間的線性相關程度,0≤ρij≤1,ρij越大表明xi和xj之間的線性相關程度越強,顯然,xi和其自身呈線性關系,即ρii=1。
為了消除標準差的影響,將協方差矩陣P分解為對角矩陣D和相關系數矩陣C。
P=DCDT
(3)
式中:D為由隨機向量中各分量的標準差,即P的對角線上的元素的正平方根組成的對角矩陣:
由相關系數的定義ρij=ρji,C為對稱矩陣。
相關系數矩陣為無量綱矩陣,其中各個元素的數值大小真正地反應了它們的重要性,即相關程度。
2.2 基于相關系數分解的平方根矩陣
根據式(3),只需要對C進行分解就可以得到P的平方根矩陣。相關系數矩陣C應當是正定對稱矩陣,可采用cholesky分解來獲得其平方根矩陣。由于cholesky分解計算量比較小,目前在確定采樣濾波器中通常采用該方法。但濾波過程中存在的各種誤差都可能導致正定的條件不能滿足,從而出現濾波失敗的情況。另外一種可用于獲得平方根矩陣的矩陣分解方法是奇異值分解,該方法對矩陣的正定性沒有要求,因此采用奇異值分解可以在矩陣出現非正定的情況下依然能獲得平方根矩陣。
對n×n維的相關系數矩陣C進行奇異值分解得:
C=UΛUT
(4)
式中:U為n×n維正交矩陣;Λ為由C的奇異值為對角線元素的n×n維對角矩陣。U的列向量組成矩陣C的列向量所在空間的標準正交基。奇異值λi滿足λ1≥λ2≥…≥λn。奇異值的大小表明了在該奇異值對應的基向量上所包含的矩陣C的信息量的大小,即在各分量相關性較高的方向上的點離中心點的距離遠。這一特點能更好地體現出采樣點的差異性。
由式(3)和式(4)得協方差矩陣的平方根矩陣為:
(5)
將狀態向量的標準差投影到Ui上,Ui為單位向量,得到狀態向量在該方向上的散布程度DUi,因此保證了每個分量的散布程度不超過其標準差。對相關系數矩陣C進行奇異值分解的結果使得采樣點能夠更準確地描述隨機狀態向量的統計特性。
3 正交變換下采樣點的優化
正交變換利用平方根矩陣對基礎采樣點的線性變換可以獲得濾波所需的采樣點,而對平方根矩陣的正交變換不會影響采樣點的分布特性。因此,可以在不改變濾波器精度的前提下,通過選擇合適的正交變換解決采樣點中存在的非局部效應。
給定正交矩陣T=[T1;T2;…;Tn][11],其中:
Tk=(βk,1,βk,2,…,βk,n)T,k=1,2,…,n
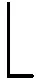
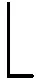
CKF的基礎采樣點可表示為[6]:
在正交變換γ=Tσ下進行采樣點優化,得到新的基礎采樣點:
qk=(qk,1,qk,2,…,qk,n)T,k=1,2,…,n
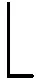
當n為奇數時,qk,n=(-1)k。由此得到的基礎采樣點γ將消除非局部效應。
i=1,2,…,n(n-1)/2
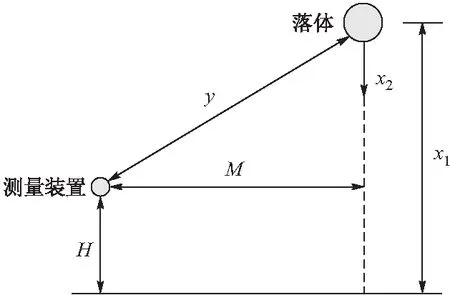
{si}={(ek+el),k {ti}={(ek-el),k 在正交變換T下該基礎采樣點變為: i=1,2,…,n(n-1)/2 采用落體跟蹤算例[2]對不同確定型濾波器及采樣點優化后對濾波結果的影響進行驗證,這里選擇UKF進行對比。如圖1所示,假設一個從空中下落的物體,其高度是x1,速度為x2,常彈道系數為x3。測量裝置的高度為H,與落體的水平距離為M。 圖1 垂直落體跟蹤幾何圖 系統方程為: 其中:wi為過程噪聲;v為量測噪聲;ρ0為海平面空氣密度;k為描述空氣密度和高度之間關系的常數;g是重力加速度。采用連續時間方程來描述系統,假定獲得量測的周期為0.5 s。系統初始條件和估計給定如下: 文獻[2]采用該模型驗證了UKF比EKF具有更好的估計效果。這里只對新濾波算法和UKF作比較。在相同運行環境下,進行50次Monte Carlo仿真,各狀態量的絕對估計誤差平均值如圖2~圖4所示。 從仿真結果看,在前10 s,落體高度和速度估計誤差逐漸增大,10 s前后估計誤差達到峰值,這是由于加速度發生了較大的變化,呈現出非常強的非線性所導致的,與文獻[12]中提到的局部方法可以處理的強非線性問題只是相對的觀點相吻合。10 s過后,估計誤差迅速減小并趨于穩定。 改進方法與UKF對落體高度和速度的估計效果相當,但其在前幾秒對落體速度的估計中新濾波算法要好于UKF,且對彈道系數的估計要明顯好于UKF。由于彈道系數直接影響加速度,故前幾秒中,改進方法對速度的估計誤差也小于UKF。這是由于彈道系數的數值遠小于高度和速度,對協方差矩陣直接進行分解,會忽略數值較小的分量,產生較大的誤差。新濾波方法將協方差矩陣分解為標準差對角陣和相關系數矩陣兩部分,對相關系數矩陣進行奇異值分解,由于相關系數是無量綱的,因此消除了數值大小的影響。在這一算例中,彈道系數的估計誤差對其他狀態量的影響較小,對系統的穩定性影響較小。但如果數值小的分量對系統穩定性影響較大,那么很可能會導致濾波發散,因此,改進方法在一定程度上提高了濾波的穩定性。 圖2 落體高度絕對估計誤差平均值 圖3 落體速度絕對估計誤差平均值 圖4 彈道系數絕對估計誤差平均值 文中首先從協方差矩陣分解的角度研究了提高濾波器穩定性的方法,其次,利用正交變換方法,在不會改變濾波精度的前提下消除了采樣點中存在的非局部效應。最后,通過仿真分析,表明改進后的優化算法具有一定的優越性。 [1] 王小旭, 潘泉, 黃鶴, 等. 非線性系統確定采樣型濾波算法綜述 [J]. 控制與決策, 2012, 27(6): 801-812. [2] JULIER S J, UHLMANN J K. A new method for the nonlinear transformation of means and covariances in filters and estimators [J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482. [3] ITO K, XIONG K. Gaussian filters for nonlinear filtering problems [J]. IEEE Transactions on Automatic Control, 2000, 45(5): 910-927. [4] MERWE R V, WAN E A. Sigma-point kalman filters for integrated navigation [C]∥Proc. of the 60th Annual Meeting of the Institute of Navigation. Dayton: Institute of Navigation, 2004: 641-654. [5] JIA B, XIN M, CHENG Y. High-degree cubature kalman filter [J]. Automatica, 2013, 49(2): 510-518. [6] ARASARATNAM I, HAYKIN S. Cubature kalman filters [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. [7] JULIER S J. The scaled unscented transformation [C]∥Proc. of American Control Conference. Anchorage: Institute of Electrical and Electronics Engineers Inc, 2002: 4555-4559. [8] MERWE R V, WAN E A. The square-root unscented kalman filter for state and parameter-estimation [C]∥Proc. of International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, Utah, 2001. [9] LEFEBVRE T, BRUYNINCKX H, DE Schuller J. Comment on “a new method for nonlinear transformation of means and covariances in filters and estimations” [J]. IEEE Transations on Automatic Control. 2002, 47(8): 1406-1408. [10] XIONG K, ZHANG H Y, CHAN C W. Performance evaluation of UKF-based nonlinear filtering [J]. Automatica, 2006, 42(2): 261-270. [11] CHANG L B, HU B Q, LI A, et al. Transformed unscented kalman filter [J]. IEEE Transactions on Automatic Control, 2013, 58(1): 252-257. [12] PEREA L, HOW J, BREGER L, et al. Nonlinearities in sensor fusion divergence issues in EKF, modified truncated SOF, and UKF [C]∥AIAA Guidance, Navigation and Control Conference and Exhibit, South Carolina, 2007. Sample Points Optimization Technique of Nonlinear Deterministic Sampling Filter WU Qingpo1,3,CONG Yuancai2,ZHOU Shaolei3 (1 No.92313 Unit, Henan Jiyuan 459000, China; 2 No.92886 Unit, Shandong Jiaozhou 266300, China; 3 Naval Aeronautical and Astronautical University, Shandong Yantai 264001, China) The selection of sample points plays a decisive role on the accuracy and stability of filter during the filter process of deterministic sampling filters. In order to improve the numerical stability of the filter, the obtained sampling points was optimized by covariance matrix decomposition, which solves the problem of the numerical influence on the distance between sample points and the mean Then the appropriate orthogonal transformation is used to eliminate the non-local effect, and it will not change the accuracy of filter under invariant theory. Finally, the effectiveness of the sample points optimization technique is validated through the simulation of a tracking problem deterministic sampling filters; sampling points optimization; covariance matrix decomposition; orthogonal transformation 2015-06-07基金項目:國家自然科學基金(61004002);航空基金(20110184)資助 吳青坡(1985-),男,河南南陽人,博士研究生,研究方向:多智能體協同控制、非線性濾波理論。 TJ55 A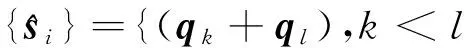
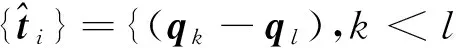
4 仿真分析
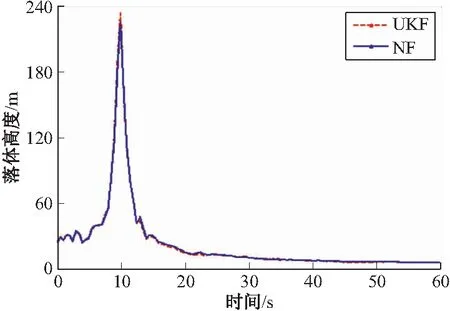
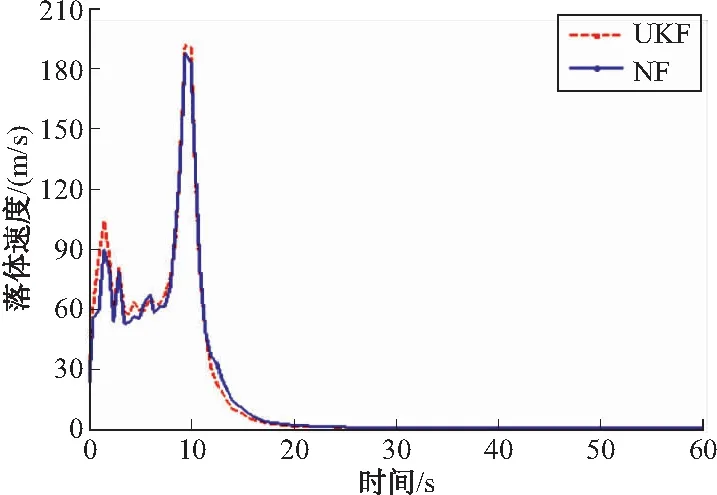
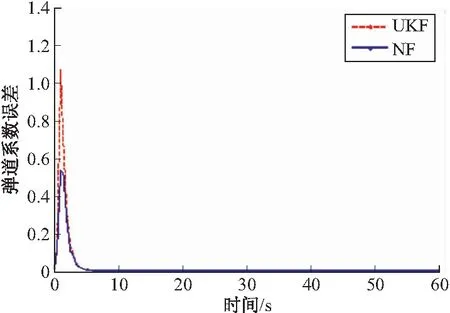
5 結論

