船載測量設備軸角編碼器誤差修正方法研究*

包 飛,倪 興,鐘德安,劉 揚

(中國衛星海上測控部,江蘇江陰 214431)

船載測量設備軸角編碼器誤差修正方法研究*

包 飛,倪 興,鐘德安,劉 揚

(中國衛星海上測控部,江蘇江陰 214431)

船載無線電測量設備進行標校時,幾套測量設備指向固定目標所測得的俯仰指向角度經修正后與大地測量所得角度存在約20″到30″的誤差。多次檢測后表明:該問題主要由設備俯仰軸角編碼器誤差導致。因此對傳統的軸角編碼器精度的檢測方法提出了新要求,增加了檢測密度和范圍,并擬合出了編碼器誤差修正公式。經過試驗任務數據驗算,該方法比以往的修正方法效果更好,該測量設備的俯仰測角總精度在原來的基礎提高了約15″。

軸角編碼器;誤差修正;精度檢測

0 引言

軸角編碼器是測量設備重要的測角部件。設備角度測量是由軸角編碼器來完成的,其基本功能是把天線各軸的機械轉角變為數字量的角度數據輸出[1]。影響軸角編碼器精度的因素很多,主要包括碼盤加工精度、旋轉變壓器的軸與天線機械軸間的耦合精度及同心度、傳感器電路引起的誤差、數碼讀出電路引起的誤差等。

船載測量設備進行標校時,幾套測量設備指向固定目標所測得的俯仰指向角度經修正后仍與大地測量所得角度存在約20″到30″的誤差。通過進一步分析發現,設備俯仰軸角編碼器雖然總的精度滿足要求,但是在具體角度上,其精度遠低于要求,導致設備的瞬時測量值誤差較大。基于此,文中以俯仰軸角編碼器為例,提出了新的軸角編碼器誤差修正方法。

1 軸角編碼器基本情況介紹

軸角編碼器主要分為直接角度編碼器和間接角度編碼器兩種。直接角度編碼器將天線軸的角位移直接轉換為數字化角度數據,可分為直讀式碼盤(如接觸式碼盤或光電碼盤[2])和“增量積累”的增量碼盤。間接角度編碼器是先將天線機械軸的轉角通過傳感器(如電位器)變為連續的物理量(電壓、時間間隔),然后再轉換為數字化角度數據。

船載測量設備軸角編碼器采用使用旋轉變壓器作為角度位移傳感器的軸角編碼器,并采用套軸式聯接來提高旋轉變壓器軸和天線機械軸間的耦合精度。

2 船載無線電測量設備軸角編碼器誤差修正現用方法

船載測量設備軸角編碼器誤差修正現用的方法主要分為兩步:第一步先檢測編碼器精度,若精度滿足指標要求(一般要求軸角編碼器精度比測量設備總精度高3～10倍[3]),則設備測角誤差可不進行編碼器誤差的修正;第二步,若編碼器精度不滿足指標要求,則通過殘差擬合進行誤差修正。

2.1 軸角編碼器精度檢測方法

對軸角編碼器精度檢測主要采用與高精度測角儀器直接比對的方法,具體檢測方法見參考文獻[4]。以俯仰軸角編碼器精度檢測為例,采用重力感應角擺儀檢測其精度包括以下步驟:

1)將角擺儀安裝在測量設備俯仰旋轉中心;

2)將天線指向俯仰為0°左右的位置,設置間隔參數為10°并清角擺儀初始讀數為0°;

3)從下往上轉動天線進行上測,每轉動10°左右停轉,并記錄角擺儀讀數Eji與設備俯仰編碼器讀數Eci直到90°;上測結束后進行下測,將天線從俯仰90°左右位置向下轉動天線,每轉動10°左右停轉,并記錄角擺儀讀數Eji與設備俯仰編碼器讀數Eci直到0°;

4)按下式計算俯仰編碼器精度:

(1)

ΔEi=(Eci-Eji)-Σ(Eci-Eji)/n

(2)

(3)

(4)

(5)

式中:n為測試的點數;ΔEi為第i次上測或下測時俯仰軸角編碼器讀數與測角儀讀數之差的殘差;σ為俯仰軸角編碼器的上測或下測的均方根誤差;Δ為上測與下測回差;δ為編碼器精度。

2.2 軸角編碼器誤差修正現用方法

軸角編碼器誤差的殘差擬合修正方法見參考文獻[5]。

3 船載測量設備軸角編碼器誤差修正改進方法

3.1 方法原理概述

從多次的實際檢測結果看,編碼器精度并不能完全反映編碼器誤差對設備測量誤差的影響,在某些角度上編碼器誤差可超過精度3倍以上,極大的影響了測量設備的測角值。為解決該問題,對原來的方法做了相關改進:

1)不再以軸角編碼器精度是否滿足要求作為誤差修正的先決條件;

2)提高檢測點密度,盡可能得到最真實的各個角度值上的實測誤差值;

3)使用具體角度值上的實測誤差值作為數據源擬合出角度測量值修正公式,直接對角度測量值進行修正而不是對最后的總測角精度進行修正,減少了中間環節誤差。

3.2 軸角編碼器誤差修正改進方法

3.2.1 誤差修正數據獲取

以俯仰軸角編碼器為例,采用3.1節中的方法,改變檢測點密度和角度范圍后得到角擺儀讀數Eji與設備俯仰編碼器讀數Eci。依據檢測點密度與角度范圍的不同,得到3組實驗數據:第一組為間隔5°一個檢測點,角度范圍為0°～180°,如表1;第二組為間隔1°一個檢測點,角度范圍為0°～90°,如表2;第三組為間隔0.3°一個檢測點,角度范圍為0°～6°,如表3。

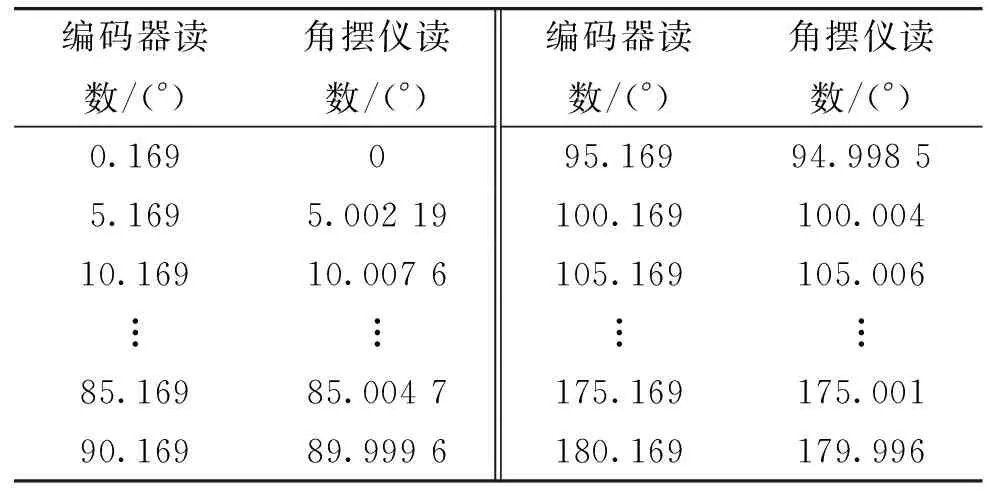
表1 ××設備俯仰軸角編碼器檢測數據(5°間隔)

表2 ××設備俯仰軸角編碼器檢測數據(1°間隔)

表3 ××設備俯仰軸角編碼器檢測數據(0.3°間隔)

3.2.2 誤差修正方法改進

將表1、表2、表3中的數據使用式(6)進行處理以得到對應的角度誤差值。

ΔEgi=(Eci-Eji)-(Ec1-Ej1)

(6)

式中:ΔEgi為俯仰軸角編碼器值誤差,即修正初始零值后的第i次上測或下測時俯仰軸角編碼器讀數與角擺儀讀數之差;Ec1為第1次上測或下測時俯仰軸角編碼器讀數;Ej1為第1次上測或下測時角擺儀讀數。

表1數據處理結果如表4所示,表2數據處理結果如表5所示,表3數據處理結果如表6所示。

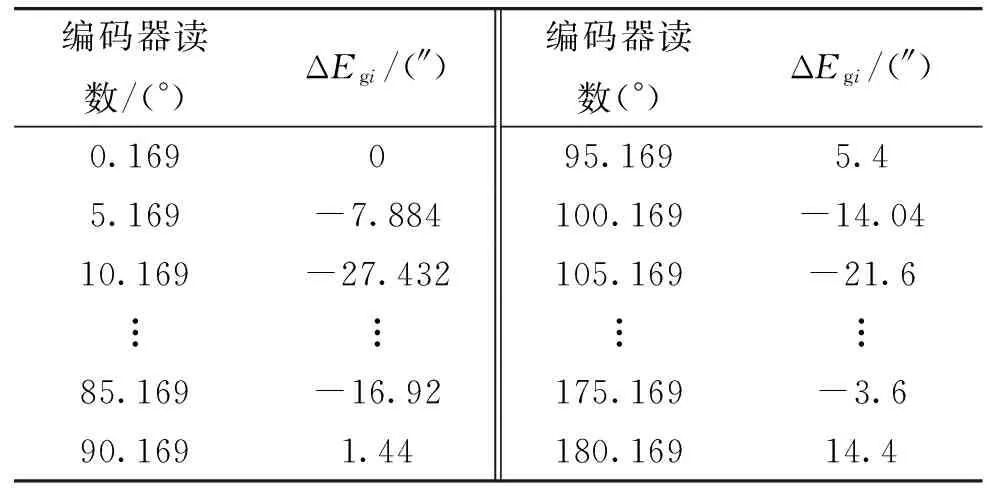
表4 ××設備俯仰軸角編碼器誤差處理結果(5°間隔)

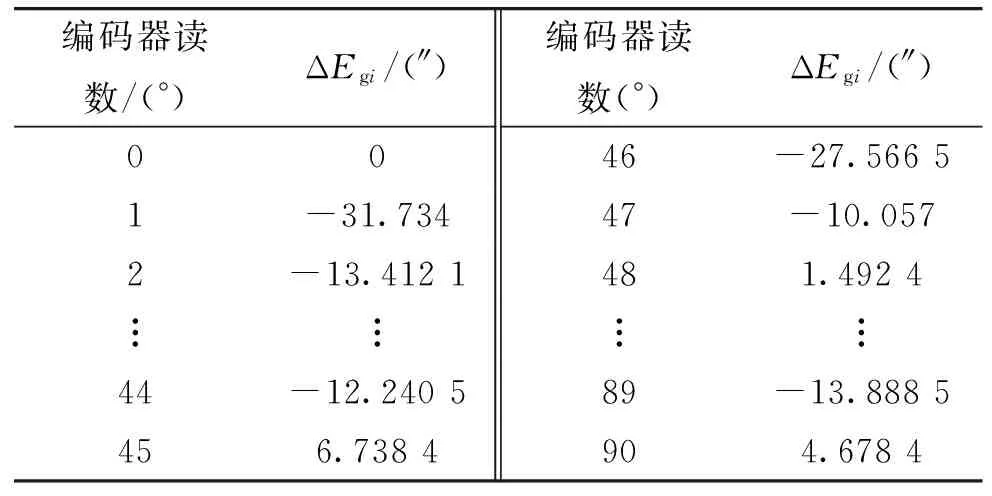
表5 ××設備俯仰軸角編碼器誤差處理結果(1°間隔)

表6 ××設備俯仰軸角編碼器誤差處理結果(0.3°間隔)

表4數據如圖1所示,圖中X軸為編碼器俯仰角度值,Y軸為ΔEgi,曲線上各點所標數值為俯仰角度值。

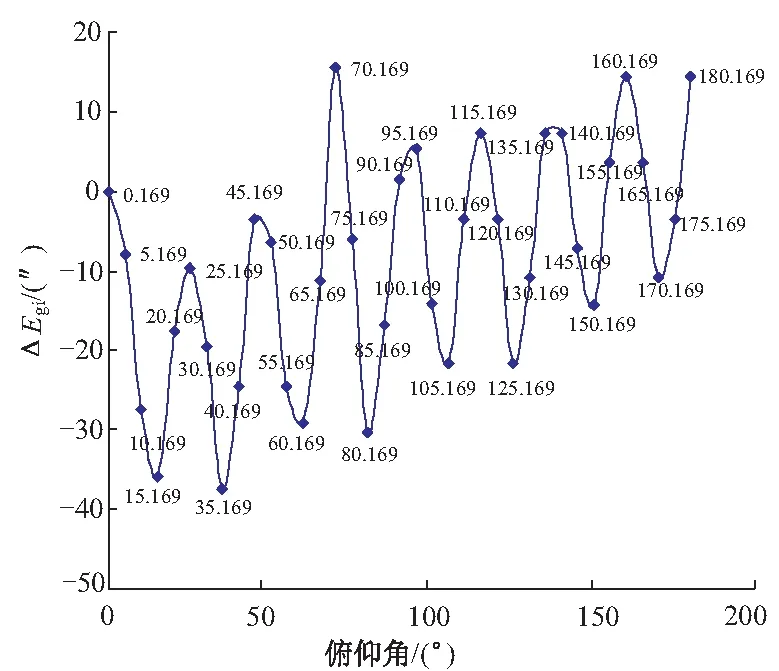
圖1 ××設備俯仰軸角編碼器誤差曲線(5°間隔)

表5數據如圖2所示,圖中X軸為編碼器俯仰角度值,Y軸為ΔEgi,曲線上各點所標數值為俯仰角度值。

圖2 ××設備俯仰軸角編碼器誤差曲線(1°間隔)

表6數據如圖3所示,圖中X軸為編碼器俯仰角度值,Y軸為ΔEgi,曲線上各點所標數值為俯仰角度值。

圖3 ××設備俯仰軸角編碼器誤差曲線(0.3°間隔)

3組實驗數據處理結果:第一組數據所得角度值誤差近似峰峰值約35″,周期約為25°的余弦或正弦函數;第二組數據所得瞬時值誤差近似峰峰值約30″,周期約為2.812 5°的余弦或正弦函數;第三組數據所得瞬時值誤差近似峰峰值約30″,周期約為2.7°的余弦或正弦函數。

經分析比較,第一組數據由于檢測間隔較大,誤差曲線不能完整反映編碼器誤差分布情況,但檢測角度范圍完整,偏心誤差可較明顯的反映出來;第二組數據與第三組數據基本吻合,認為較真實的反應編碼器誤差分布情況,但所測角度范圍較窄,因此,對誤差曲線進行擬合時需結合第一組數據。

綜合3組誤差曲線數據分布規律,擬合可得該編碼器角度誤差近似公式:

ΔEg=-15sin(128Ec-90°)+0.08Ec-15

(7)

式中:Ec為編碼器讀數,單位為(°);ΔEg為編碼器瞬時值誤差參數,單位為(″)。

3.3 軸角編碼器誤差修正改進方法的效果驗證

將該設備執行的多個任務的俯仰角測量數據作為數據源,經式(7)修正后重新進行測量精度處理,并與原來的精度處理結果做比較。

下面給出4個進入的任務數據驗證情況,如表7所示:設備標準模式下2個進入的殘差均值分別變小了15.6″和14.9″,殘差均方根值分別變小了0.3″和變大了2.5″;擴頻模式下2個進入的殘差均值分別變小了16.3″和12.5″,殘差均方根值分別變小了4.8″和4.7″。

從數據處理結果看,設備的俯仰系統誤差的殘差均值和隨機誤差的殘差均方根值均得到改善,設備俯仰角測角總精度較以往提高了約15″,軸角編碼器誤差修正效果較好。

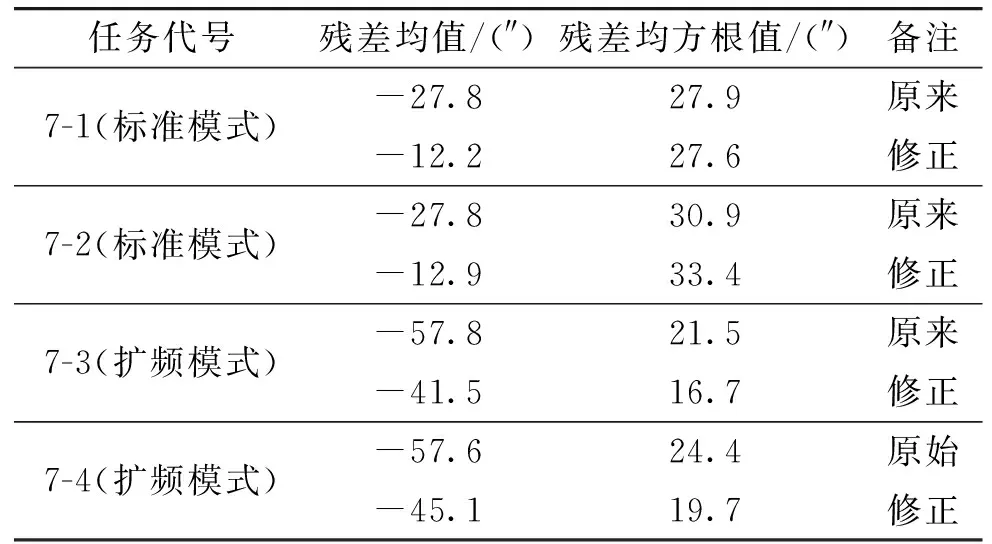
表7 ××設備俯仰軸角編碼器誤差修正驗算情況

4 結束語

無線電測量設備軸角編碼器誤差對設備的測量精度有著直接影響,通過實測軸角編碼器在各角度值上的誤差并進行數學擬合,得到了誤差與角度值的關系公式,經任務數據驗證,使用該公式進行軸角編碼器誤差修正后設備測量總精度較以往得到明顯提高。但該方法還存在一定的局限性,所得的誤差公式是由實測誤差值擬合而來,因此不同的軸角編碼器其誤差公式不同,即誤差公式不能通用。

[1] 趙業福, 李進華. 無線電跟蹤測量系統 [M]. 北京: 國防工業出版社, 2001: 98.

[2] 羅世魁, 王國強, 王繼新, 等. 偽隨機碼在絕對式光電軸角編碼器中的應用 [J]. 光學精密工程, 2003, 11(6): 596-601.

[3] 江文達, 陳道桂. 航天測量船 [M]. 北京: 國防工業出版社, 2002: 36-38.

[4] 鐘德安. 航天測量船測控通信設備標校與校飛技術 [M]. 北京: 國防工業出版社, 2009: 99-100.

[5] 鐘德安, 包飛, 張同雙, 等. 測量設備軸角編碼器誤差修正研究 [J]. 無線電工程, 2012, 42(9): 51-53.

Research on Error Correction in Axial Angle Encoder of Ship-borne Measuring Equipments

BAO Fei,NI Xing,ZHONG De’an,LIU Yang

(China Satellite Maritime Tracking and Controlling Department, Jiangsu Jiangyin 214431, China)

When ship-borne wireless measuring devices are measuring and calibrating, they have 20″ to 30″ error value between the angle values got by measuring devices and that got by the earth measuring. According to tests, the problem is mainly caused by the error of axis angle encoder. So, new requirements were made for detection method of the axial angle encoder, detection density and scope increased, and correction formula of the encoder error was fit. After the test checking, the effect is better than the previous methods, the total accuracy of the measuring equipment has been improved by about 15″.

axial angle encoder; error correction; precision detection

2015-10-12

包飛(1981-),男,江蘇淮安人,工程師,碩士,研究方向:標校、校飛。

V557

A