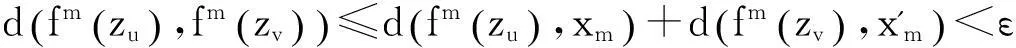漸近平均偽軌跟蹤性質、弱specification性質和分布混沌
王立冬,王 翔,劉 恒
(1.大連民族大學 a理學院;b環境與資源學院,遼寧 大連116605;
2.大連理工大學 數學科學學院,遼寧 大連 116024)
?

漸近平均偽軌跟蹤性質、弱specification性質和分布混沌
王立冬1a,2,王翔1b,2,劉恒1a,2
(1.大連民族大學 a理學院;b環境與資源學院,遼寧 大連116605;
2.大連理工大學 數學科學學院,遼寧 大連 116024)
摘要:證明了有漸近平均偽軌跟蹤性質的非平凡緊致動力系統具有一致分布混沌或者按序列分布混沌。此外,在具有漸近平均偽軌跟蹤性質系統中的分布混沌在測度中心是一致和稠密的,即有一個不可數的一致分布混沌集是由這樣的點組成,它們的軌道閉包包含測度中心。作為一個推論,具有弱specification性質的系統也有類似的結果。
關鍵詞:漸近平均偽軌跟蹤;弱specification性質;分布混沌;按序列分布混沌
最近,在具有specification性系統中的分布混沌已被深入研究[1-5]。最新的一個成果是,具有Specification性的系統一定具有一致稠密的分布混沌,且若它有一個不動點,可表現出稠密不變的一致分布混沌[5]。
既然弱specification性和AASP都比specification性質弱,那么就有這樣一個問題:它們中任何一個是否具有分布混沌?盡管文獻[6]中證明了具有AASP和兩個周期點的系統一定具有李約克混沌,但距離這個問題的答案還很遠。
本文對這個問題做出了正面的解答,帶有AASP(或者弱specification性質)的非平凡系統如果有兩個弱周期點,則具有一致分布混沌。
1預備知識
設(X,d)是一個至少有兩個點的緊致度量空間。f:X→X是連續映射。
f的測度中心記為M(f), 是所有不變測度的所有支撐集并的閉包。易知,X-M(f)對任何不變測度都是零測度集。如果對于任意ε>0 存在正整數M使得對所有n≥1,#{i;0≤i 0=j1≤k1 存在點z∈X 使得下列條件成立: (1)d(fi(z),fi(ym))<δ 對于所有m≤s以及i,(jm≤i≤km) 成立; (2)fn(z)=z, n=ks+Nδ; 就稱f有specification性。 定義2[8-9]如果S?X 包含至少兩個點,對于任意x,y∈S 且x≠y 時滿足: 就稱S 是一個分布混沌集。如果f有一個不可數分布混沌集,稱f分布混沌。 2漸近平均偽軌跟蹤的非平凡系統 本節證明如果一個具有AASP的非平凡系統(或者弱specification性)有至少兩個幾乎周期點,那么它具有一致分布混沌,否則它具有按序列的分布混沌。 由引理1, 存在稠密度為零的集合J1,J2?+滿足當m?J1時并且當m?J2時。 令J=J1∪J2,則J也是稠密度為零的集合,這樣對于m?J都有 對所有滿足tni≤m =1。 假設i足夠大且滿足tki≥K則對于滿足tki≤m 因此 對所有滿足tki≤m =0。 因此,對所有 推論1假設f有弱specification性并且有一個具有全支撐集的不變測度,那么f具有傳遞一致分布混沌。 參考文獻: [1]DOLE?ELOVáJ.Distributionallyscrambledinvariantsetsinacompactmetricspace[J].NonlinearAnalysis:Theory,Methods&Applications,2013,79:80-84. [2]OPROCHAP.Specificationpropertiesanddensedistributionalchaos[J].DiscreteandContinuousDynamicalSystems,2007,17: 821-833. [3]OPROCHAP,TEFáNKOVáM.Specificationpropertyanddistributionalchaosalmosteverywhere[J].ProceedingsoftheAmericanMathematicalSociety, 2008, 136: 3931-3940. [4]SKLARA,SMíTALJ.Distributionalchaosoncompactmetricspacesviaspecificationproperties[J].Journalofmathematicalanalysisandapplications, 2000, 241: 181-188. [5]WANGH,WANGLD.Theweakspecificationpropertyanddistributionalchaos[J].NonlinearAnalysis:Theory,Methods&Applications, 2013,91: 46-50. [6]NIUYX,SUSB.Onstrongergodicityandchaoticityofsystemswiththeasymptoticaverageshadowingproperty[J].Chaos,Solitons&Fractals, 2011, 44: 429-432. [7]ZHOUZL.Weaklyalmostperiodicpointandmeasurecenter[J].ScienceinChinaSeriesA,1993, 36 : 142-153. [8]SCHWEITZERB,SMíTALJ.Measuresofchaosandspectraldecompositionofdynamicalsystemsoftheinterval[J].TransAmerMathSoc, 1994,344:737-754. [9]OPROCHAP.Distributionalchaosrevisited[J].TransAmerMathSoc, 2009,361: 4901-4925. [10]WANGLD,HUANGGF,HUANSM.Distributionalchaosinasequence[J].NonlinearAnalysis:Theory,Methods&Applications, 2007,67: 2131-2136. [11]WALTERSP.AnIntroductiontoErgodicTheory[M].NewYork:Springer-verlag, 2000: 43. (責任編輯鄒永紅) Asymptotic average shadowing property, almost specification property and distributional chaos WANG Li-dong1,2,WANG Xiang2,3,LIU Heng1,2 (1.School of Science, Dalian Minzu University, Dalian Liaoning 116605, China; 2.School of Mathematical Science, Dalian University of Technology, Dalian Liaoning 116024, China; 3. School of Environment and Resource, Dalian Minzu University, Dalian Liaoning 116605, China;) Abstract:It is proved that a non-trivial compact dynamical system with asymptotic average shadowing property displays uniformly distributional chaos or distributional chaos in a sequence. Moreover, distributional chaos in a system with asymptotic average shadowing property can be uniform and dense in the measure center, that is, there is an uncountable uniformly distributionally scrambled set consisting of such points that the orbit closure of every point contains the measure center. As a corollary, the similar results hold for the system with almost specification property. Key words:asymptotic average shadowing property; almost specification property; distributional chaos; distributional chaos in a sequence 中圖分類號:O189 文獻標志碼:A 文章編號:2096-1383(2016)01-0043-04 作者簡介:王立冬(1955-),男,吉林德惠人,教授,博士,學校特聘教授,博士生導師,主要從事拓撲動力系統研究。 基金項目:國家自然科學 (11271061);中央高校基本科研業務費專項資金資助項目(DC201502050201)。 收稿日期:2015-11-19;最后修回日期:2015-11-27