Weibull分布在航空武器項目經費管理中的應用研究

劉浩敏

(中國空空導彈研究院，河南 洛陽　471000)

?

Weibull分布在航空武器項目經費管理中的應用研究

劉浩敏

(中國空空導彈研究院，河南 洛陽471000)

摘要：科學、合理的經費估算可以為項目立項與經費安排提供重要的決策參考；基于Weibull分布理論，首先提出了一種基于累計經費約束的最小二乘分布參數估計法，給出了幾個常用的項目累計經費約束條件；其次運用提出的方法，對其在航空制導武器項目經費管理中的應用進行了研究；最后對應用情況進行了綜合分析。

關鍵詞：Weibull分布；累計經費約束；最小二乘

本文引用格式：劉浩敏.Weibull分布在航空武器項目經費管理中的應用研究[J].兵器裝備工程學報，2016(1):102-105.

Citation format:LIU Hao-min.Study on Air-Borne Project Cost Management by Weibull Distribution [J].Journal of Ordnance Equipment Engineering,2016(1):102-105.

隨著新技術和新材料的廣泛應用，加之技術難度大、系統復雜、不可遇見因素多，航空制導武器項目日益增長的研制成本和有限的經費預算之間的矛盾越來越突出，如何科學、合理地估算出項目總研制經費及其各年度的投資強度，對項目立項決策、經濟性評估、合理分配有限經費資源及對其進行有效管理具有重要意義[1-5]。

研究發現，Weibull分布模型在一定條件下能較好地描述大型項目時間與經費之間的分布關系，即如果研制過程基本按計劃進行，無大的突發性變更和干擾，則在項目整個研制過程中，時間-經費的分布表現為中間多、開始和結束時少的特點。基于這種分布特性，國內許多學者和項目管理人員對其在各類項目經費管理中的應用做了大量研究。徐哲等[6]對Weibull分布模型的特點、應用范圍、參數估計方法等進行了較為詳細的理論研究，并對其在大型復雜系統研制經費預估等方面做了應用研究；郭基聯等[7]運用已有裝備項目的歷史數據對Weibull分布模型的參數估計方法進行了研究，并根據項目的特點，導出了分布參數的取值范圍，減小了主觀因素對參數估計的影響；胡葦[8]對Weibull分布模型在航天項目研制經費管理中的應用做了較為深入的研究，并對其應用過程中存在的問題進行了具體分析；謝紅勝等[9-10]基于Weibull分布建立了水電設備費用模型，并據此解決了水電設備維護費用模型中的不確定性問題。

目前，Weibull分布模型在航天、兵器等領域項目經費管理中已有較多應用研究，但在航空制導武器項目方面的應用較少。從目前我國航空制導武器項目經費管理相對落后的現狀來看，有必要對其在航空制導武器項目經費管理中的應用進行研究。此外，通過對Weibull分布模型進行研究發現，只有當時間趨于無窮大時其分布函數才會趨于1，即當時間趨于無窮大時項目所有經費才能執行完畢，但在實際過程中，項目研制周期是有限的，其所有經費必須在有限時間內執行完畢，或者說基本執行完畢(99.5%以上)。分析Weibull分布模型在相關領域中的應用發現，應用Weibull分布模型給出的項目經費分布在項目結束時往往還有大量經費“待執行”。

本文基于Weibull分布模型，對其在航空制導武器項目經費管理中的應用進行研究，提出基于累計經費約束的最小二乘分布參數估計法，可解決運用傳統最小二乘法面臨的存在大量經費“待支出”問題。最后，對Weibull分布模型在航空制導武器項目經費管理中的應用進行綜合分析。

1Weibull時間-經費分布模型

Weibull時間-經費概率分布函數的通用表達式為

(1)

其中，K為項目總研制經費，表示投資規模；參數a決定了曲線的陡度，表示投資的急迫性；參數m決定了分布曲線的峰值位置，表示項目投資的最高點；參數r為位置參數，表示研制階段的起始點，一般取0表示研制周期的開始時刻，所以，通常情況下，Weibull時間-經費分布函數的表達式為

(2)

在項目研制過程中，由于經費實際上并不完全按照理論情況連續發生，所以其累積分布模型在實際過程中應用的更多。Weibull時間-經費的累計分布模型為

(3)

其中，F(t)為第t時期末累積發生的經費總額。設第t時期所需的研制經費為ΔF(t)，則

(4)

由式(3)和式(4)可以看出，如果知道參數m和a就可以確定總投資額為K的項目研制周期內的投資強度分布和各個時間段內的累計投資額。

2基于累計經費約束的最小二乘分布參數估計

目前，較常用的參數估計方法有經驗估計法、線性回歸法和高斯-牛頓迭代法等，但研究發現，通過此類方法估算出的參數確定的經費分布在項目結束時往往還存在大量經費“待支出”，總體精度較差。本文給出一種基于累計經費約束的最小二乘參數估計法可以較好地解決此類問題。

2.1傳統最小二乘分布參數估計法

線性最小二乘法運用的對象是線性方程，顯然式(3)所描述的方程為典型的非線性方程，根據文獻[10]，式(3)可線性化為如下形式：

Y=A+BX

(5)

其中，Y=ln(ln(K/(K-F(t))))；A=lna；B=m；X=lnt。

假設已知關于變量X,Y的n對觀測數據(Xi,Yi)(n=1,2,…,n)，則根據線性最小二乘原理，在此有如下方程成立：

(6)

(7)

E為觀測值Yi和(A+BXi)之差的平方和，即誤差的平方和。求解上述方程即可得到參數A和B的最小二乘估計值。運用項目實際發生數據驗證發現，采用傳統最小二乘法擬合出的經費分布曲線在項目結束時仍然還有較大部分的經費“待支出”，總體擬合效果不理想。

2.2最小二乘分布參數估計法

研究發現，傳統最小二乘法對分布參數進行估計的基礎為已知的n對觀測數據，基于這n對觀測數據估算出的分布參數(或者說分布曲線)與觀測數據直接相關，也就是說，由這n對觀測數據在一定約束條件下(觀測值Yi和(A+BXi)之差的平方和最小)確定的分布曲線是觀測值的一種數學反映。基于此，為了使分布曲線能有效反映項目結束時的狀態，我們可以在觀測樣本中增加期望的項目結束樣本信息，進而可實現對項目結束時的經費支出情況進行約束。

1) 項目結束時累計支出經費占總經費比例為99.5%的約束條件為

lna+mlnT=ln(ln200)

(8)

2) 項目研制時間進行到一半時累計支出經費占總經費比例為50%(即時間過半、任務過半)的約束條件為

lna+mln(T/2)=ln(ln2)

(9)

3) 項目研制時間進行到t(0≤t≤T)時刻末時累計支出經費占總經比例為η(0≤η≤1)的約束條件為

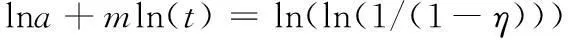
(10)

3實例分析與應用

下面以我國某航空制導武器項目為例，運用基于累計經費約束的最小二乘分布參數估計法，從上述3個方面分別進行應用研究。表1給出了我國某航空制導武器項目的歷史數據，本節后續的應用研究將以此為依據。由于保密原因，數據進行了處理，但不影響研究結果的給出。

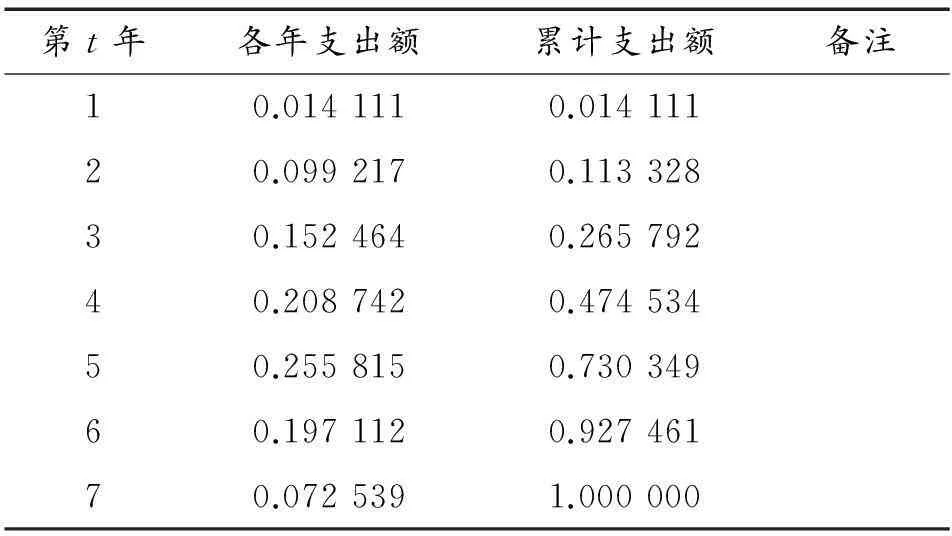
表1　某項目歷史數據

3.1事后評估應用

根據表1給出的歷史數據，基于式(6)和式(7)式描述的傳統最小二乘法，很容易得出m值和a值分別為2.823 014和0.014 686。在傳統最小二乘法的基礎上，增加式(8)描述的累計經費約束方程，可得出一組新的m值和a值分別為2.925 198和0.013 720。根據兩種方法確定的m值和a值，可以給出兩種方法確定的項目累計支出擬合值，詳見表2和圖1。

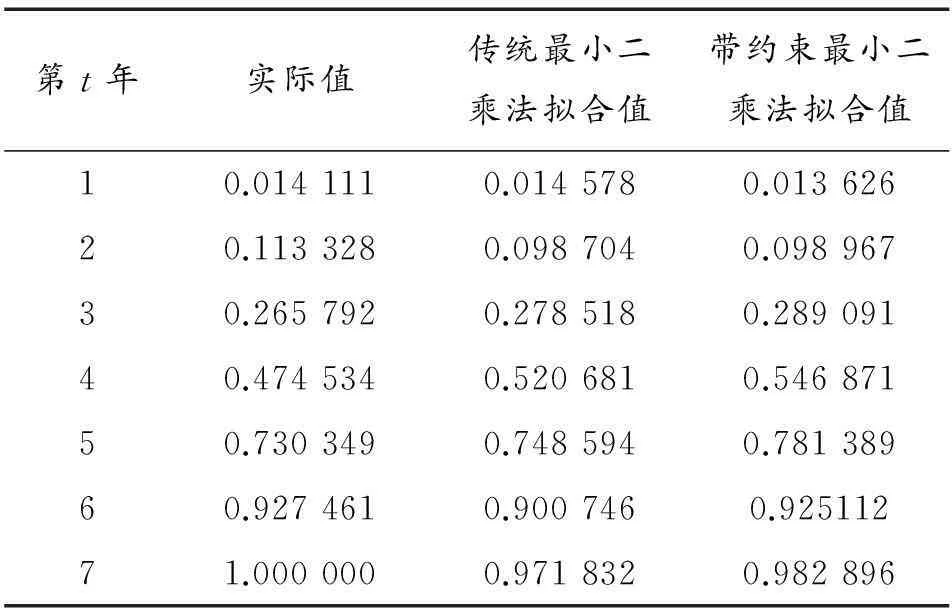
表2　兩種方法擬合數據對比

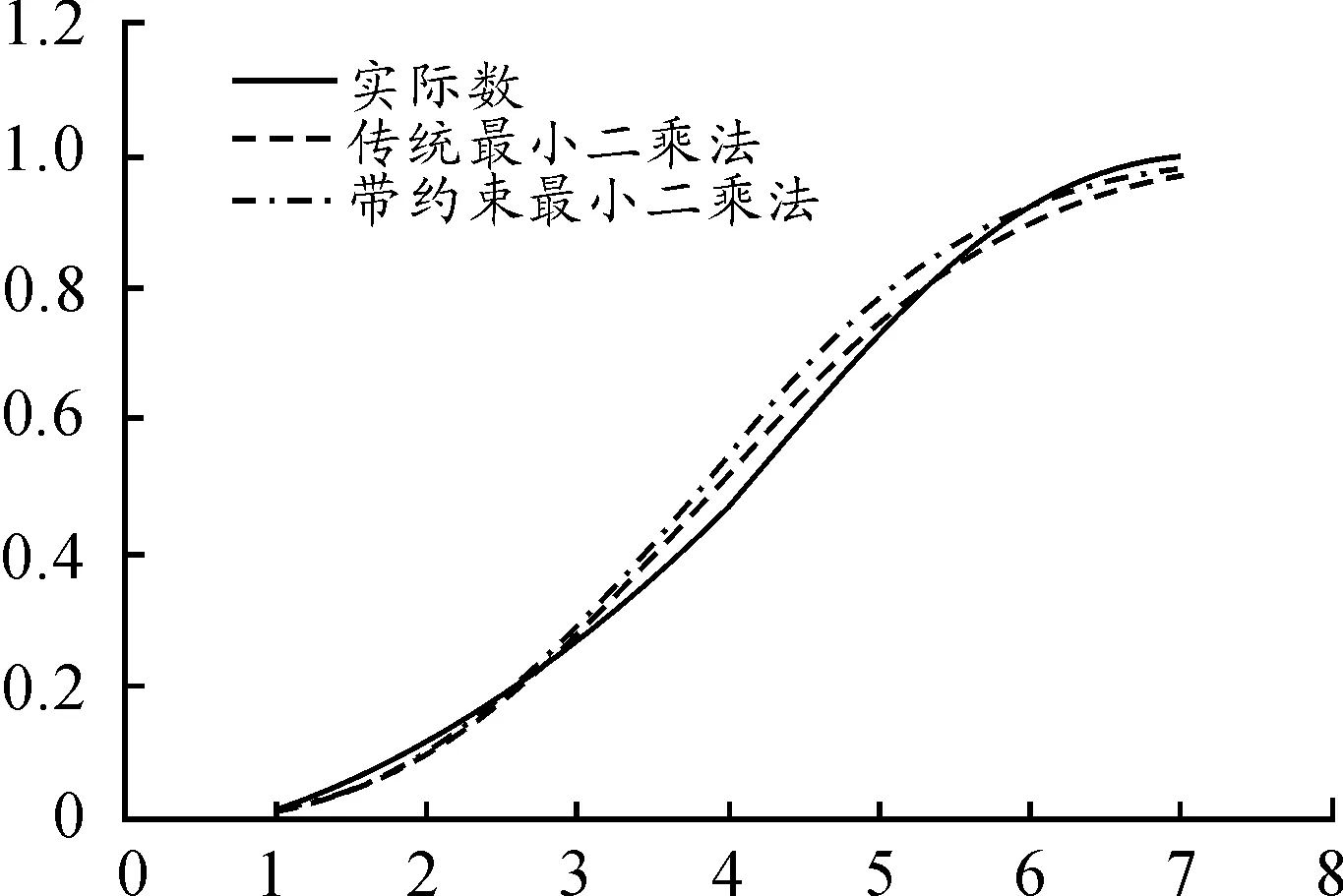
圖1　兩種方法擬合數據對比

從對比數據可以看出，在項目結束的第7年，采用傳統最小二乘法擬合的累計支出額為0.971 832，“待支出額”為0.028 168，而采用帶約束的最小二乘法擬合的累計支出額為0.982 896，“待支出額”僅為0.017 104，較傳統方法減小了0.011 064，累計擬合效果有了較大改善。

3.2事中預測應用

仍然以表1給出的數據為例，假設項目目前進行到第4年末，前4年的累計支出數據已知，分別用傳統最小二乘法和帶約束的最小二乘法對后續三年的支出情況進行預測。經計算，采用傳統最小二乘法給出的m值和a值分別為2.745 082和0.015 333，采用帶約束的最小二乘法給出的m值和a值分別為2.961 309和0.013 587，兩種方法給出的預測數據詳見表3和圖2。

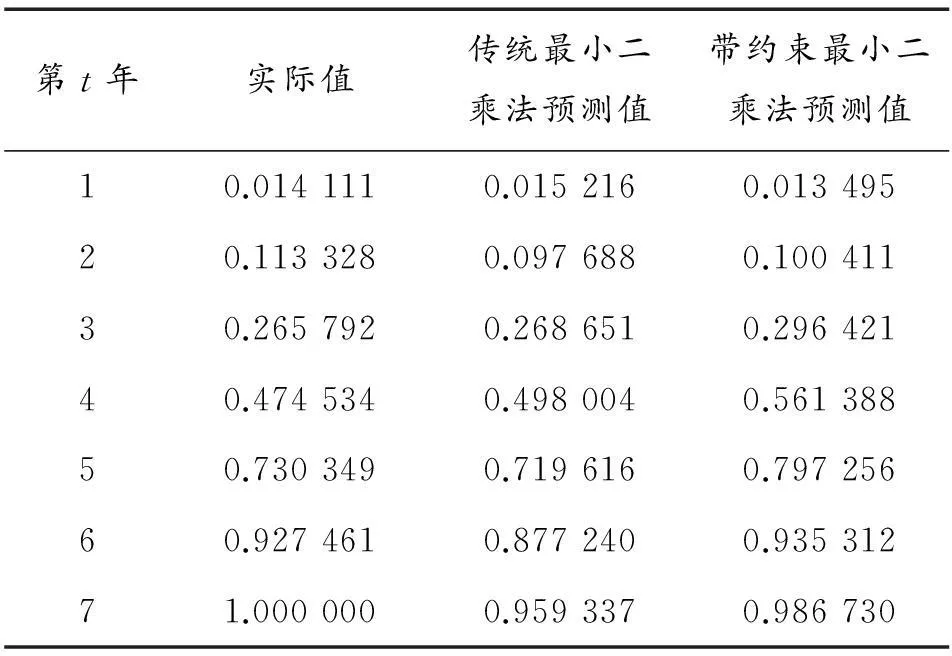
表3　兩種方法預測數據對比

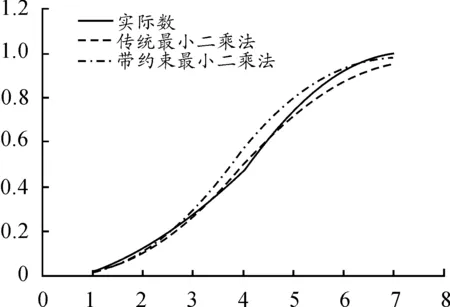
圖2　兩種方法擬合數據對比

從表3對比數據可以看出，在項目結束的第7年，傳統最小二乘法預測的累計支出值為0.959 337，“待支出額”達0.040 663，而帶約束的最小二乘法預測的累計支出值為0.986 730，“待支出額”僅為0.013 270，兩種方法預測的累計誤差額相差3倍之大。

3.3事前預估應用

在實際項目管理過程中，往往會有“時間過半、任務過半”的進度要求。根據項目掙值管理理論，任務過半也即預算過半。若項目研制過程基本按計劃執行，其時間和經費分布服從Weibull分布，則“時間過半、任務過半”的Weibull理論實現就可以用約束式(9)來描述。基于此，在項目前期規劃過程中，如果對項目開始年份和中間年份的經費管理給出一定要求，比如項目第一年支出占項目總經費的1%，中間年份累計支出占項目總經費的50%等，就可以對項目整個研制周期內的經費安排情況進行初步預估。

為了對事前預估的效果做對比評估，本節仍然以前面給出的某項目為估算對象。假定在項目開始規劃過程中，第1年項目支出占總經費的比例為1%，第4年累計支出占總經費的50%，即“時間過半、任務過半”，第7年，也即項目結束年，累計支出占總經費的99.5%。運用前面介紹的方法，我們可以得到一組m值和a值分別為2.997 390和0.013 385，并由此給出的各年度預估值和累計預估值分別見表4、圖3和表5、圖4。

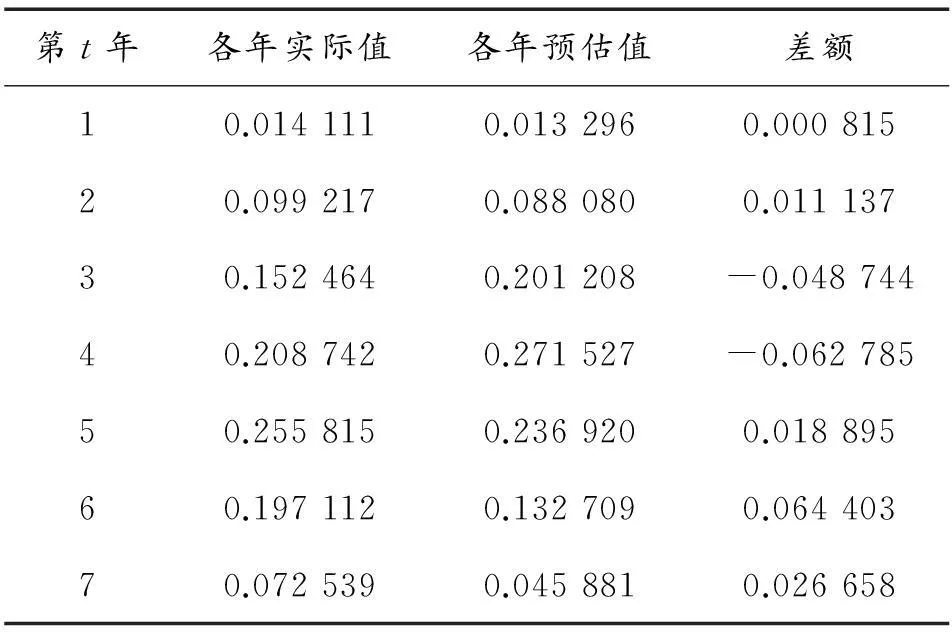
表4　預估各年度數據與實際數據對比

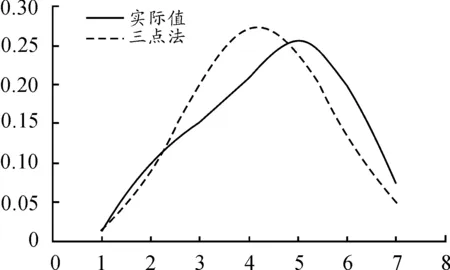
圖3　預估各年數據與實際數據對比

從表4和表5對比數據可以看出，規劃(預估)的項目累計支出與實際累計支出總體相差較小，僅有1.04%，但各年度規劃(預估)額與實際支出額之間的差異較大，規劃的經費支出峰值與實際相差1年。分析項目實際研制過程發現，在第3年和第4年期間，早期規劃的某關鍵技術沒有按照原計劃節點順利突破，某重大外場試驗因天氣原因沒有按時完成，進而導致其對應的經費沒有按照計劃(預算)執行。也就是說，項目實際并沒有嚴格按照理論過程進行，其實際支出與規劃存在較大差異。

綜上分析，如果項目嚴格按照計劃開展，過程中沒有大的變更，運用基于累計經費約束的最小二乘法對項目研制經費進行預估能收到較好的效果，可以為項目決策者提供較有力的決策依據。

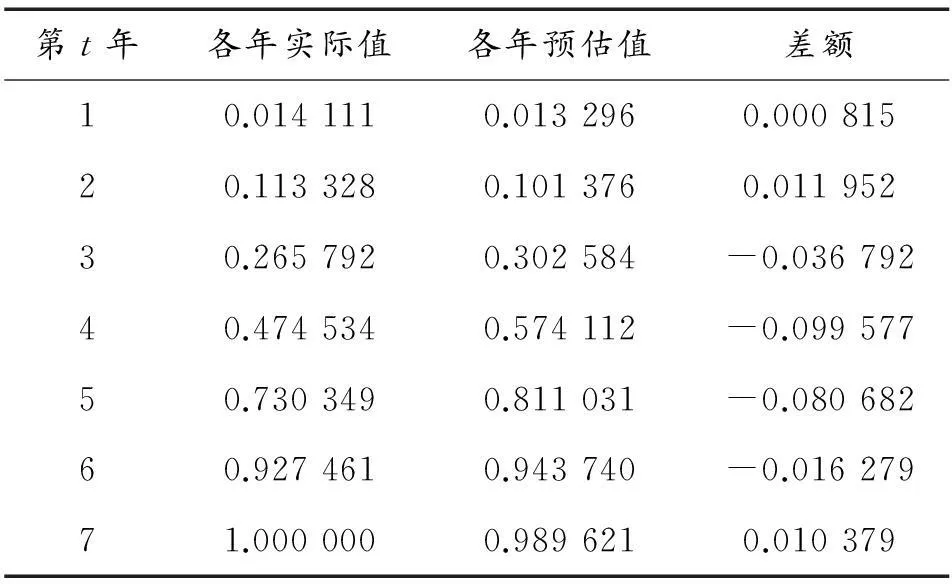
表5　預估各年累計數據與實際數據對比

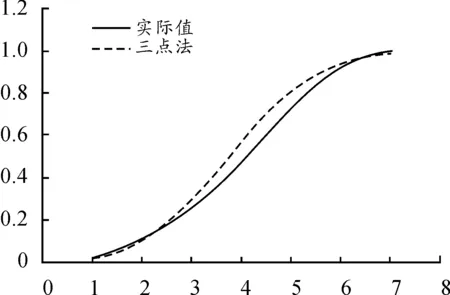
圖4　預估各年累計數據與實際數據對比

3.4應用綜合分析

從上述應用研究結果可以看出，不論是傳統最小二乘法還是本文提出的帶約束最小二乘法給出的累計結果與實際值均存在一定偏差，從航空制導武器項目經費管理實際情況來看，累計誤差在2%以內是完全可以接受的。實際上，在項目經費的具體管理過程中，一般允許留有一定的不可預計費，不同項目不可預見費比例不一樣，通常情況下可以按照項目總經費的3%計算，研究結果中2%左右的誤差對應的經費額在實際應用過程中可以按照不可預見費來考慮。

此外，對于大型復雜項目，不確定因素多，研制周期長，其研制過程往往不能完全按照事先計劃進行，其經費投入也往往不是呈現為單峰值分布，而是雙峰值或多峰值分布。針對此類項目，可先把大型復雜項目分解為若干子項目，然后對各子項目采用上述方法分別進行研究，最后疊加即可得到整個項目的研究結果。

4結束語

針對傳統最小二乘參數估計法存在的問題，本文以Weibull時間-經費分布模型為基礎，提出了基于累計經費約束的最小二乘法，給出了幾種常用的期望累計經費樣本約束條件。為了驗證本文所提方法的有效性，以某項目為例，從事后評估、事中預測和事前預估3個方面進行了應用研究，研究結果表明，與傳統最小二乘法相比，本文提出的發放具有更好的項目累計經費擬合效果和后續經費預測效果，對我國航空制導武器項目經費管理具有較大的指導意義和應用價值。

參考文獻：

[1]陳士濤，張志峰，歸建洲.基于Weibull分布的武器系統研制時間-費用模型[J].四川兵工學報,2008,29(2):39-41.

[2]馮自立，陳曉陽，顧家銘.Weibull分布下基于矩法的小樣本量定時截尾數據的估計[J].四川兵工學報,2010,31(3):93-97.

[3]唐薇.衛星型號研制工程計劃進度和經費管理技術研究[D].南京：南京航空航天大學，2011.

[4]漆鑫.航天產品全壽命周期成本的控制和管理研究[D].上海：上海財經大學，2008：19-26.

[5]徐輝，陶慶，王濤.產品研制費用的Weibull累計曲線擬合模型[J].北方工業大學學報，1997，9(3):54-57.

[6]徐哲，馮允成.復雜系統研制費用Weibull分布的研究[J].北京航空航天大學學報，1998，24(2):224-227.

[8]胡葦.威布爾時間-費用模型在航天型號研制經費管理中應用的再思考[J].航天工業管理，1994(8)：14-18.

[9]謝紅勝，吳春誠，吳相林，趙勇.基于威布爾分布的水電設備費用模型研究[J].華中科技大學學報(自然科學版)，2006，34(9)：54-56.

[10]徐哲.武器裝備項目進度、費用與風險管理[M].北京：國防工業出版社，2011.

(責任編輯唐定國)

【后勤保障與裝備管理】

Study on Air-Borne Project Cost Management by Weibull Distribution

LIU Hao-min

(China Airborne Missile Academy, Luoyang 471000, China)

Abstract:Scientific and appropriate cost estimating of project can be used in making important strategic decision for project application and project budget planning. Firstly, based on the Weibull distribution theory, a new least squares parameter estimating method that was based on total cost constraint and some common constraint conditions about total cost constraint of project were presented. Secondly, the article discussed the application in the air-borne project using the theory presented. Finally, a comprehensive analysis was summed up.

Key words:Weibull distribution; total cost constraint; least squares

文章編號：1006-0707(2016)01-0102-05

中圖分類號：V219

文獻標識碼：A

doi:10.11809/scbgxb2016.01.024

作者簡介：劉浩敏(1982—)，男，碩士，工程師，主要從事航空制導武器總體設計、航空制導武器項目經費管理等研究。

收稿日期：2015-06-25；修回日期：2015-07-15