艦艇裝備保障網絡的抗毀性分析

張　肖,戴明強,邵　帥

(海軍工程大學 理學院，武漢　430033)

?

艦艇裝備保障網絡的抗毀性分析

張肖,戴明強,邵帥

(海軍工程大學 理學院，武漢430033)

摘要：艦艇裝備保障是海軍后勤保障工作的重要環節，科學構建保障網絡是提高保障效率的前提和基礎；深入開展艦艇保障網絡研究，對提高裝備保障工作效益具有重要意義；針對保障網絡節點繁多、線路交錯的特點，分析了保障網絡的復雜特性，構建基于復雜網絡理論的保障網絡模型，設計保障網絡的拓撲特征參數，研究了保障網絡的抗毀性；理論分析和實驗結果表明：遭到隨機攻擊時保障網絡的抗毀性要大于選擇性攻擊，節點被攻擊時保障網絡的抗毀性小于邊被攻擊；處于保障流程末端的碼頭之間有更多的互連路徑對整個網絡的抗毀性也有較高的貢獻。

關鍵詞：艦艇裝備保障；復雜網絡理論；抗毀性

本文引用格式：張肖,戴明強,邵帥.艦艇裝備保障網絡的抗毀性分析[J].兵器裝備工程學報，2016(1):97-101.

Citation format:ZHANG Xiao, DAI Ming-qiang, SHAO Shuai.Analysis of Survivability of Warship Equipment Support Network[J].Journal of Ordnance Equipment Engineering,2016(1):97-101.

艦艇裝備保障是海軍后勤保障工作的重要組成部分，承擔著沿海一帶地區將艦艇航行所需物資從后方倉庫運送到部隊的任務，統籌好艦艇裝備保障對于艦艇戰斗力的發揮具有重要意義。艦艇裝備保障涉及到保障網絡規劃、倉庫選址、路徑優化等等，只有科學地構建裝備保障網絡，充分發揮保障網絡的整體效能，才能有效提高艦艇后勤保障的效率。艦艇裝備保障網絡是一個包含了不同種類節點和錯綜復雜線路的復雜系統。網絡的節點包括保障基地、倉庫以及各橋梁、路口、港口碼頭等交通樞紐，節點眾多、性質復雜；網絡的邊包括各等級的公路、鐵路以及水路和空運等，距離長短不一，網絡流量易受本身通行能力及外部環境影響[1]。

具有自組織、自相似、吸引子、小世界、無標度中部分或全部性質的網絡可以稱為復雜網絡[2]，1998年Watts與Strogatz提出的小世界網絡概念和1999年Barabasi與Albert提出的無標度網絡概念開創了現代復雜網絡理論研究的先河[3-4]。此后復雜網絡的抗毀性引起了越來越多的研究人員的關注，他們從不同的角度以及采用不同的方法研究了復雜網絡的抗毀性[5-7]。本文在對裝備保障網絡復雜特性進行分析的基礎上，構建了基于復雜網絡理論的裝備保障網絡模型，設計了裝備保障網絡的拓撲特征參數，對幾種不同的攻擊模式進行了仿真實驗，得出的結論對下一步相關的研究給出了參考。

1復雜網絡的基本拓撲特征

對于一個網絡來說，它的拓撲結構對其性質有著重要的影響，而用于描述復雜網絡拓撲結構的特征也有許多，本文重點選擇對網絡中節點與邊的度和介數來進行研究。

1.1度和度分布

一個節點的度通常定義為該節點連接的所有邊的總和。網絡的度分布即為網絡中節點的度的概率分布或者頻率分布。而度的分布情況可以用分布函數P(k)來描述，表示了一個隨機選定的節點度數恰好為k的概率分布。

度分布函數反映了網絡的宏觀統計性質，是現階段網絡分類的主要依據之一。小世界網絡模型中，節點度分布是泊松分布，而無標度網絡的度分布則是冪律分布。隨機網絡的度分布也是泊松分布，顯示了網絡中度分布比較均勻，不存在度數過高或過低的節點。

1.2介數和介數分布

節點的度這一指標通常作為節點重要的特性進行研究，它能夠在一定程度上反映這個節點在網絡中的重要性，但不能完全反映其在網絡中所處的地位。介數就是用來描述相應節點或邊在整個網絡中作用和影響力的參量。節點的介數為網絡中所有的最短路徑中經過該節點的數量[8]。假設任意兩個節點j與k之間的最短路徑為σjk，其中經過節點的最短路徑為σjk(i)，則節點i的介數反映的是節點i在節點j與k之間的重要程度，可以表示為

(1)

同度分布類似，介數分布表示的是隨機選定的節點的介數恰好為Bi的概率分布。累積介數分布函數表示的是介數不小于Bi的節點的概率，如式(2)所示：

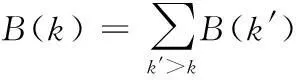
(2)

邊介數的定義與節點介數類似，可以定義為通過該邊的節點對之間的最短路徑的數目，邊e的介數反映的是邊e在節點g與h之間的重要程度，可以表示為

(3)

2艦艇裝備保障網絡的復雜性分析

艦艇裝備保障網絡是由多個互相區別又互相聯系的單元結合起來，以完成艦艇物資器材流動為目的的有機結合體。

2.1裝備保障網絡結構和節點的復雜性

網絡結構的復雜性通常體現在網絡的大規模性和行為的統計性、連接結構的復雜性、網絡連接的稀疏性等方面，而且艦艇裝備保障網絡通常會呈現出復雜的層次結構。因此，隨著艦艇物資種類的不斷更新和艦艇裝備保障范圍的不斷擴大，為滿足不同保障目標的需求，艦艇裝備保障的網點將不斷增加，艦艇裝備保障網絡會呈現出大規模發展的趨勢。

艦艇裝備保障網絡包含多種各自獨立的實體，構成某一特定網絡的實體在地理上一般是分散的，組織結構、技術水平、資源狀況、職能等許多方面也不盡相同。由于地理位置特點，有時也會存在兩節點之間存在業務關系而沒有地理連接的情況[9]，這說明其節點自身存在復雜性。

2.2各種復雜性因素的相互影響

艦艇主要部署在沿海一帶，所以裝備保障網絡會受到沿海地理和水文氣象以及其他各種因素的作用和影響，從而使得網絡產生時間和空間上演化的復雜性。影響裝備保障運輸效果的因素有很多。其中動態因素包括戰爭因素影響、極端天氣侵襲、車流量變化、道路施工、目的地的變動、可供調動的車輛變動和非戰時敵特破壞等；靜態因素如所保障部隊的分布區域、道路交通網絡、車輛運行限制等。這些因素之間的相互影響以及對保障網絡的影響使得網絡在一定的時間和空間內進行演化，成為更加復雜的網絡。

3艦艇裝備保障網絡模型構建

裝備保障問題可以說是一項復雜的系統工程。最基本的情況是，被保障單位會根據自己遂行的作戰與訓練任務，提出裝備上的包括配齊配件和裝備修理等保障需求，然后上報至保障指揮中心，中心來統籌和協調下屬的倉庫以及搶修隊來具體實施。完成一次裝備保障所需要的基本流程可以抽象并簡化成如圖1所示的環路。

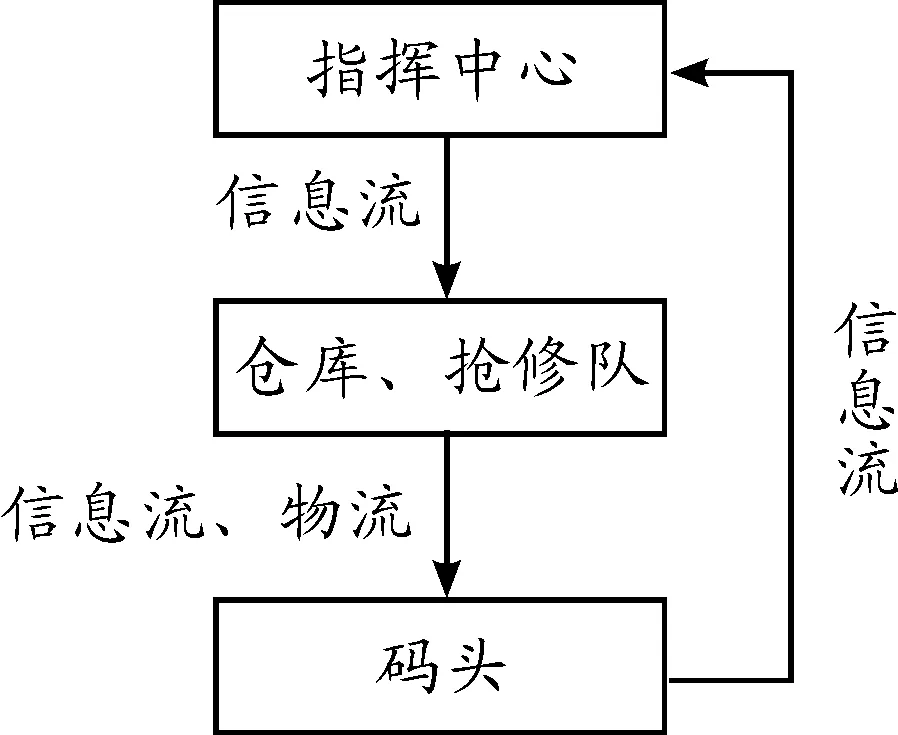
圖1　保障流程

本文所研究的流程部分是指揮中心下達任務給倉庫及搶修隊后，倉庫及搶修隊做出反應去基層單位對艦艇進行裝備保障。依據復雜網絡理論，將網絡體系中指揮管理、倉庫和保障實體等抽象為網絡節點，實體間復雜的相互關系抽象為邊，將網絡體系抽象為作艦艇裝備保障網絡。即將航材配送網絡抽象為一個由節點集合V和邊集合E組成的網絡圖G(V,E)。艦艇裝備保障網絡顯然是一個加權網絡，各邊的權值則是根據實際路徑長度、路徑可靠性、安全性、承載力、平均流量等因素綜合考慮。其次，雖然實際中的物流或者信息流已完全能實現雙向連通，但是本文主要研究的流程對象是單向物流的裝備保障，所以本保障網絡為有向加權網絡。通常會用鄰接矩陣來描述網絡中節點的相鄰關系，再根據連接情況將各邊的權值賦予矩陣中如下所示，式(4)為圖2加權網絡的鄰接矩陣：

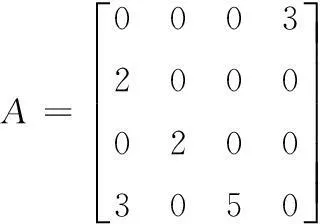
(4)

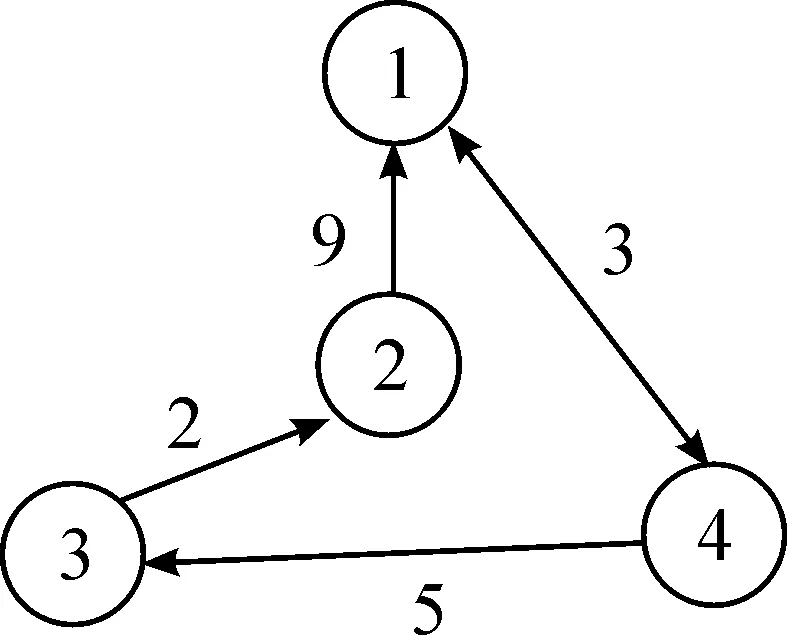
圖2　有向加權網絡示例

3.1模擬艦艇裝備保障網絡的構建

首先構建一個模擬網絡，包括指揮中心1個，倉庫3個，需要保障的單位9個，共13個節點。其中有向邊則為實際可行的路徑，邊上的數值則表示該條邊歸一化后的權值，共26條邊。根據設定的參數，運用ucinet軟件得到圖3。

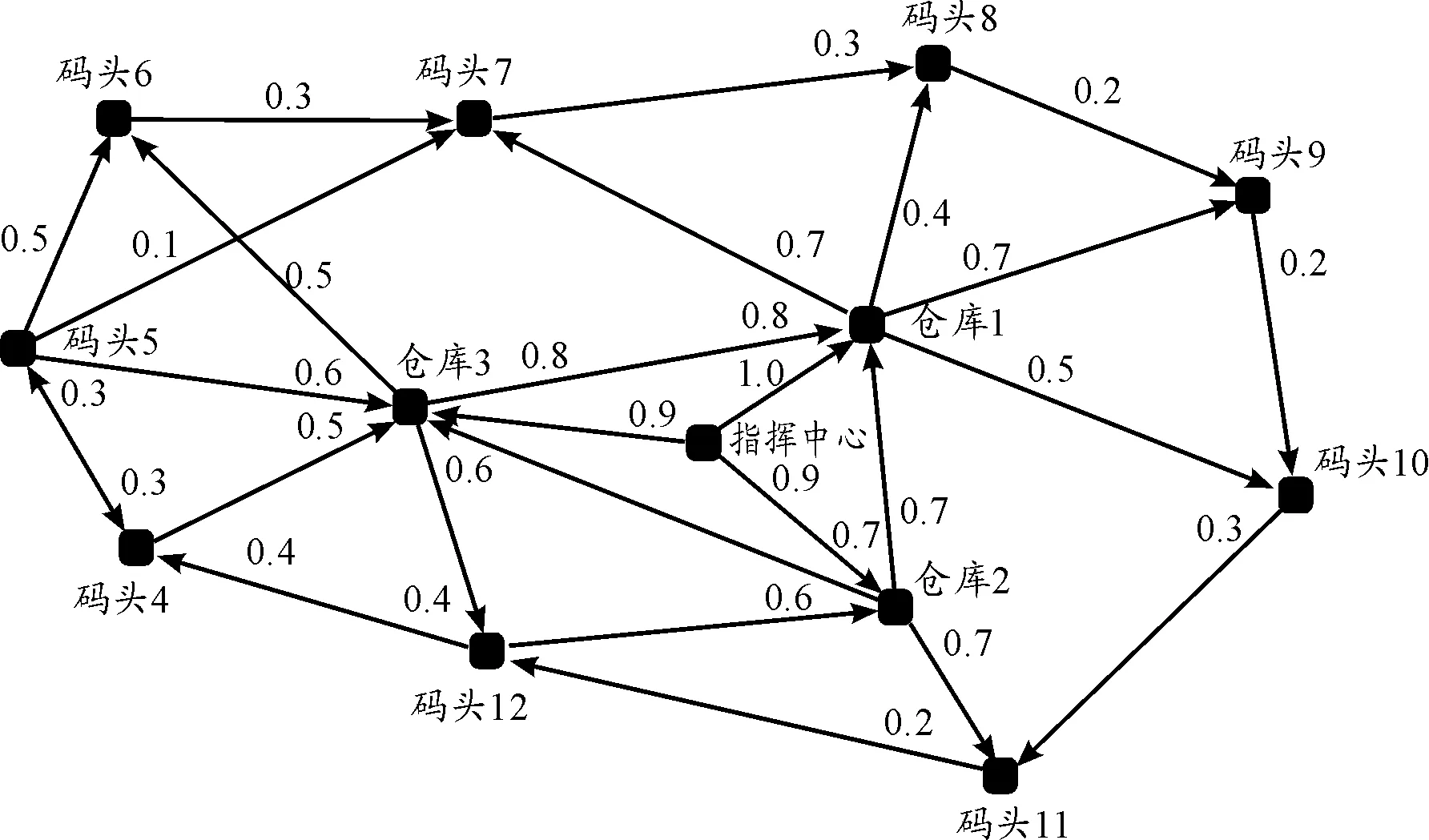
圖3　模擬艦艇裝備保障網絡示意圖

3.2網絡參數的計算方法

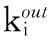
(5)

節點的介數表現出了信息流經該節點的可能性，節點的介數值會隨著經過該節點的信息流的變化而增大或減小，是動態變化的，利用介數這個統計特性能夠找到信息負載大的網絡節點。介數越大，說明流經該節點的數據分組就越多，該節點就越重要。由于介數可以反應出一個網絡的動態特征，因此，它是分析裝備保障網絡中配送中心重要程度和網絡受到影響后出現動態變化的重要特征參量。考慮到保障網絡為有向網絡，記ωjk表示節點j與k之間通過節點i的最短路徑的權值，在式(2)的基礎上，可以將保障網絡的的介數表示為

(6)

3.3網絡抗毀性指標的確立

由于裝備保障網絡具有典型的無標度特性，利用復雜網絡理論能夠有效分析裝備保障網絡的抗毀性并為網絡的設計和維護提供支持。本文采用了應用最為廣泛的抗毀性指標―網絡全局效率[10]進行分析。網絡全局效率的定義如下：

(7)

式(7)中G表示網絡圖，N為網絡中節點的總數，dij為節點i和節點j之間的最短距離。

4仿真實驗

圖3中的指揮中心入度為0，是網絡的頂點。考慮當其遭到攻擊時整個網絡將會癱瘓，抗毀性為0，所以優先攻擊其他各節點，最后再移除指揮中心。

按照式(5)和式(6)利用Matlab軟件可以計算各節點度和介數以及邊的介數，結果歸一化后如表1和表2所示。

采用5種攻擊方式進行模擬，具體算法如下：

① 對網絡中的節點進行隨機移除。

Step 1用rand函數在1～12產生一個隨機數。

Step 2在將鄰接矩陣中將隨機數對應的行和列置空。

Step 3根據式(7)計算此時的網絡效率。

重復Step 1、2、3。每重復一次，隨機數的范圍大小減1。依此操作直到鄰接矩陣置空為0。

② 對網絡中的節點按度的大小依次移除。

Step 1將表1中得到的節點度數用sort函數得到從大到小排序后的度數數組和與之對應的節點號數組D(i)。

Step 2將D(1)在鄰接矩陣對應的行和列置空。

Step 3計算此時的網絡效率。

重復Step 2、3。每重復一次前，D(n)與D(n-1)作比較。D(n)>D(n-1)時，節點號數組內元素均減1，即D(n)=D(n)-1；否則不進行操作。依此操作直至鄰接矩陣置空為0。

③ 對網絡中的節點按介數的大小依次移除。利用 bgl工具包中的betweenness_centrality函數可以得到節點與邊的介數，余下算法參照②中步驟。

④ 對網絡中的邊進行隨機移除。

Step 1將③中得到的邊的信息存儲賦值到一個 3×26的新矩陣E(i,j)中。其中第一行是邊的起點，第二行是邊的終點，第三行是邊的介數。

Step 2用randperm函數產生一個從1～26順序打亂的隨機數組R(i)。

Step 3選取隨機數R(1)，得到所對應在E(i,j)中的起點E(1,R(1))和終點E(2,R(1))，并將鄰接矩陣中對應的元素置inf。

Step 4計算此時的網絡效率。

依次選取隨機數，重復Step 3、4，直至R(26)。

⑤ 對網絡中的邊按介數的大小依次移除。具體算法參照②③④。

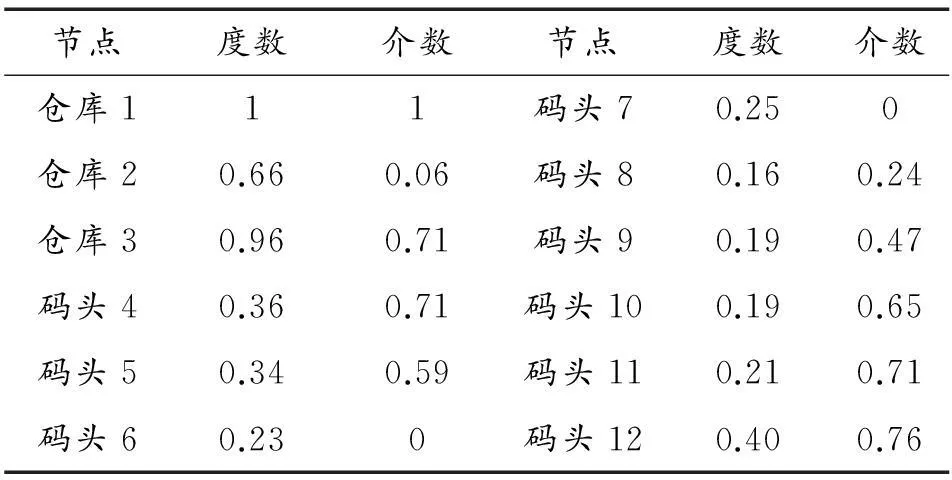
表1　各節點的度數和介數

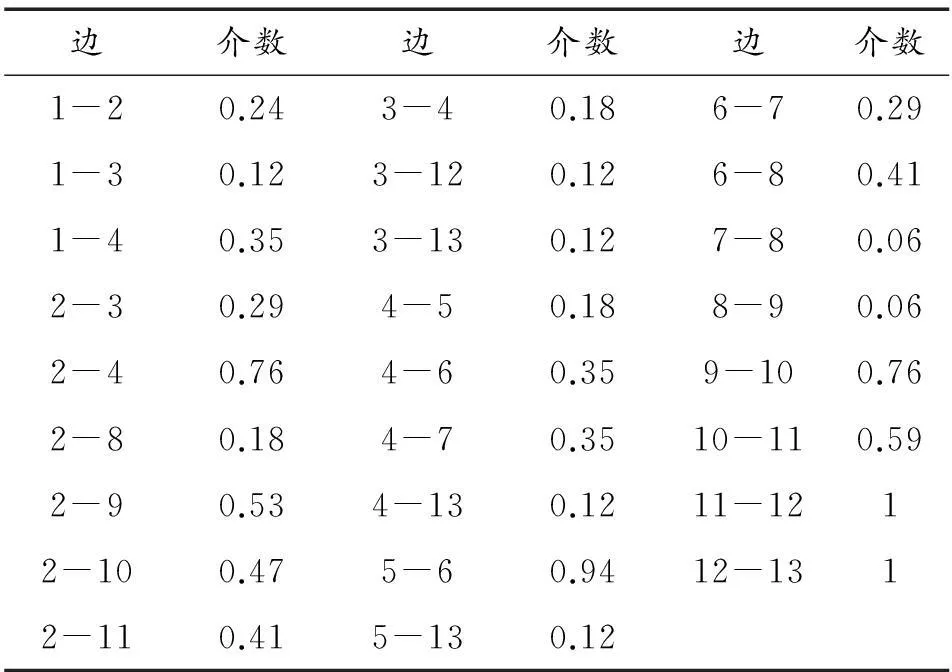
表2　各邊的介數

采用5種攻擊方式對網絡模型進行攻擊后，得到了網絡效率隨節點數和邊數變化情況圖，如圖4所示。

從圖4可以看出對節點進行高介數攻擊后網絡效率大幅下降，僅攻擊了最高介數的一個點后網絡效率就降低至50%；在攻擊到第5個節點后網絡效率和受到隨機攻擊時的網絡效率的下降速度大致相當。這說明在攻擊的前面幾步選擇高介數攻擊會對網絡造成更大的傷害。整個過程來看高介數攻擊對網絡的打擊也是最大的。當節點被隨機攻擊時，攻擊后網絡效率的下降則是均勻的、線性的。而當節點被高度數次序攻擊時，到第2、3個節點網絡效率沒有出現大幅度的下降。這是因為這兩個節點分別對應倉庫3和倉庫2，而這兩個倉庫所對應的被保障單位之間有更多的雙向連接，從而使在倉庫2、3被移除后大部分的保障路徑依然存在。

從圖5中可以看出邊在隨機攻擊和高介數攻擊兩種方式下的抗毀性大致相當。

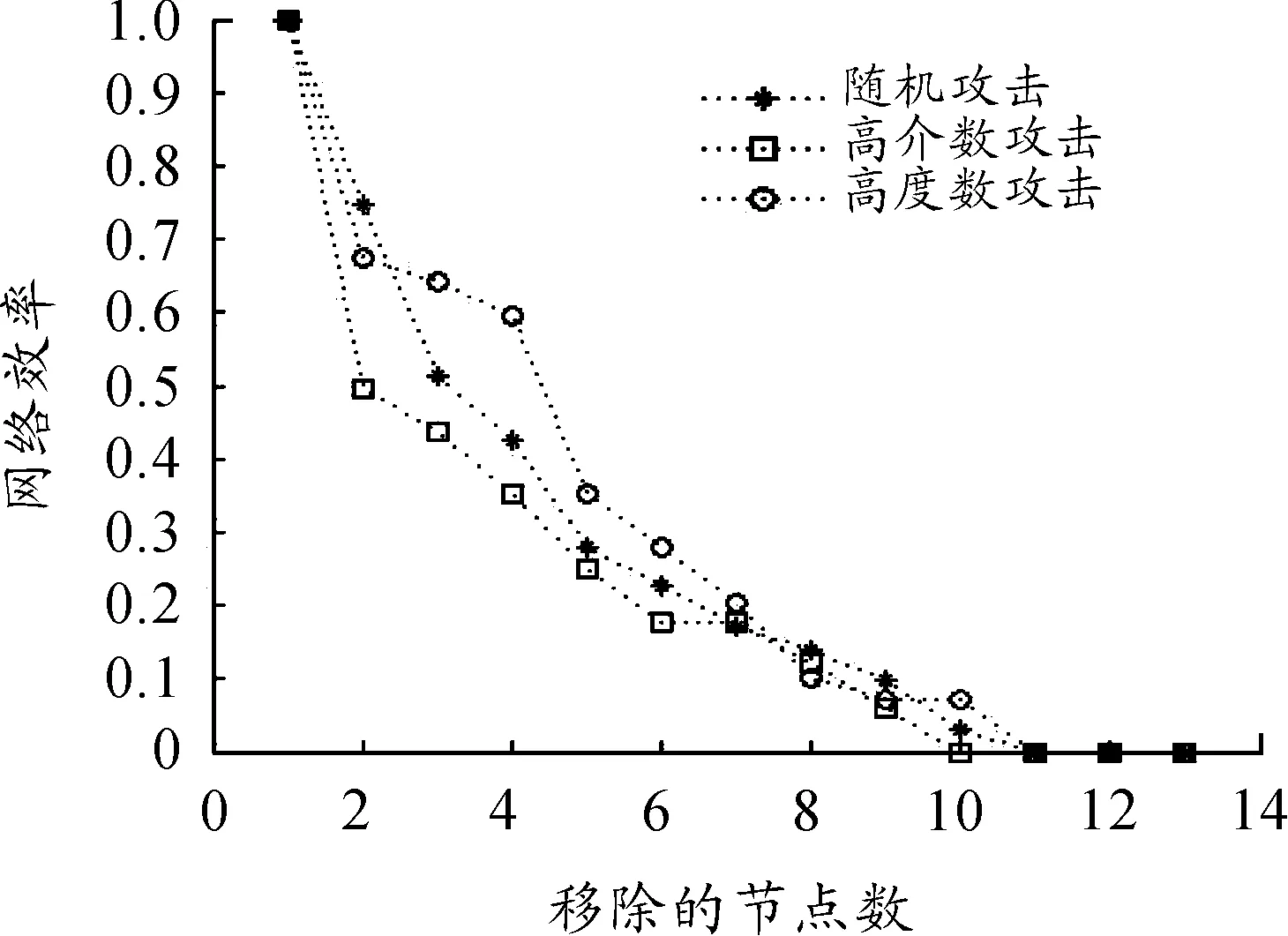
圖4　節點移除與網絡效率關系

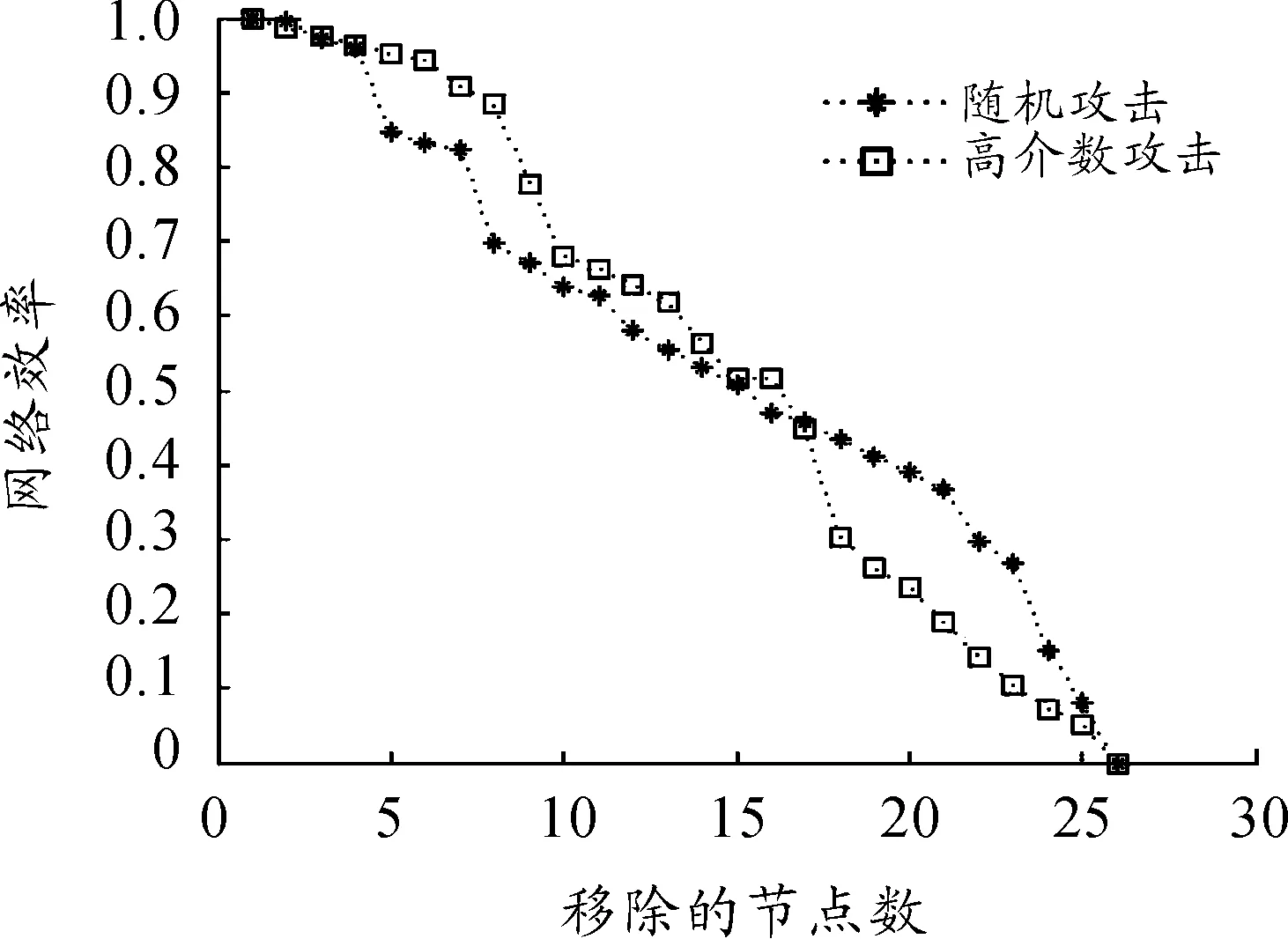
圖5　邊移除與網絡效率關系

邊的移除個數為26，而節點的個數為13，考慮在比較節點與邊被攻擊時網絡效率的參考不統一，這里把節點的移除個數進行了乘以2的處理之后得到了圖6和圖7，可以看出在兩種攻擊模式下，移除節點對網絡的傷害遠大于移除邊。這是因為一個節點的移除會順帶讓與之相關聯的邊均失效，這也說明節點對網絡抗毀性的意義要遠大于邊。

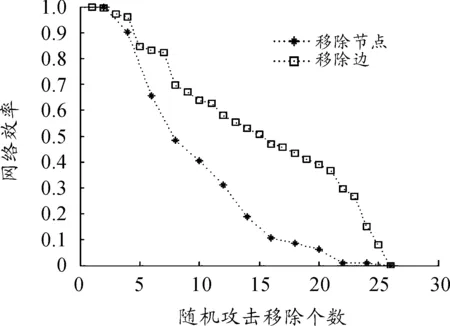
圖6　隨機移除邊與節點的網絡效率比較

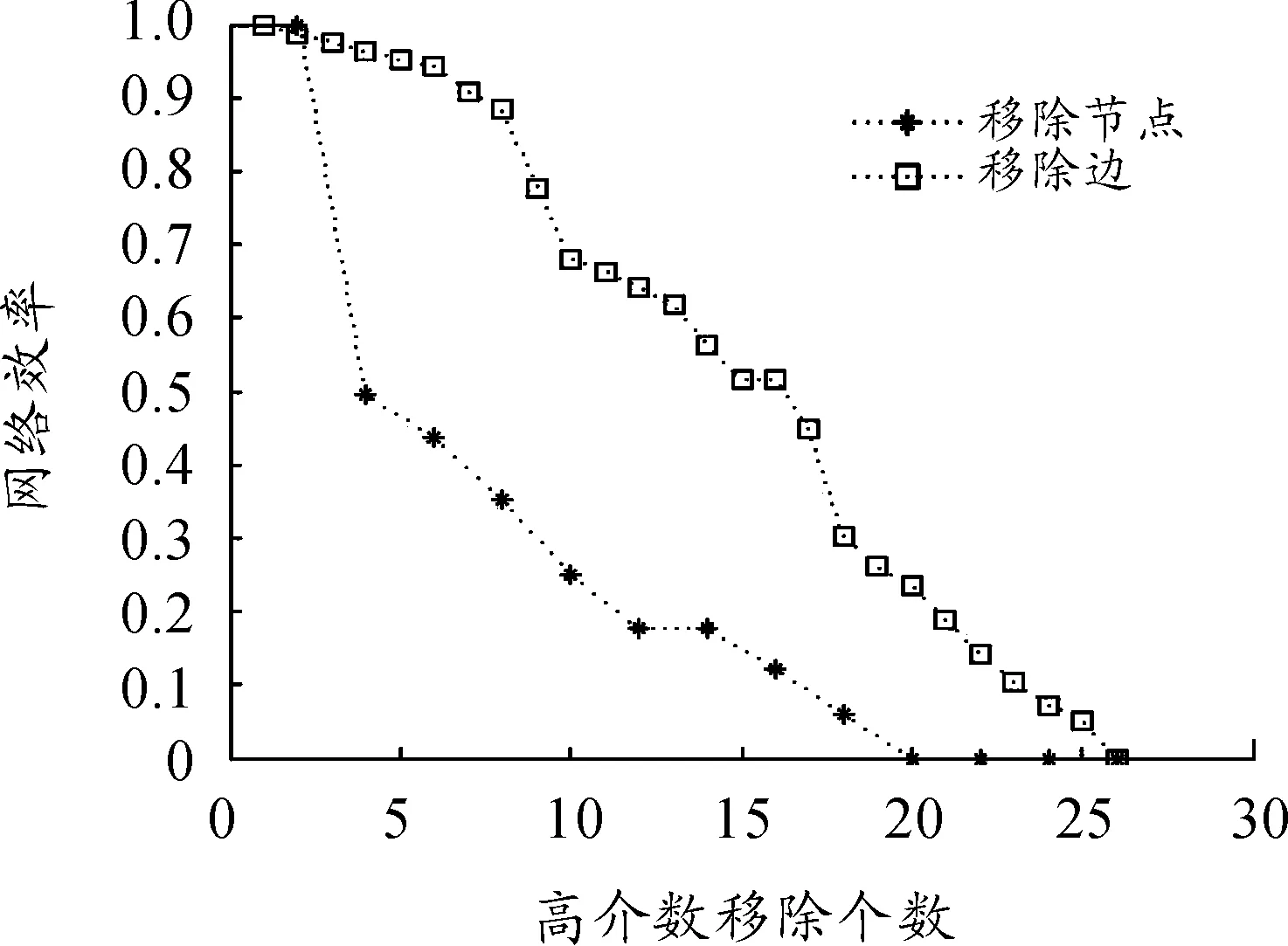
圖7　高介數移除邊與節點的網絡效率比較

5結論

本文從艦艇裝備保障網絡的特點出發，引入復雜網絡理論，分析了保障網絡的結構特征和抗毀性。在分析了艦艇裝備保障網絡復雜性的基礎上，利用復雜網絡理論構建了艦艇裝備保障網絡的拓撲模型，給出了艦艇裝備保障網絡的拓撲特征。最后，利用構建的艦艇裝備保障網絡拓撲模型分析了艦艇裝備保障網絡的抗毀性，為艦艇裝備保障網絡的設計提供了有效支持。理論分析和實驗結果表明，隨機攻擊時保障網絡的抗毀性要大于選擇性攻擊，節點攻擊時保障網絡的抗毀性小于邊攻擊。處于保障流程末端的碼頭之間有更多的互連路徑對整個網絡的抗毀性也有較高的貢獻。在進行艦艇裝備保障網絡規劃時，可依據出現隨機攻擊或者選擇攻擊的概率大小合理規劃網絡布局。

參考文獻：

[1]王鐵寧,于雙雙,梁波.軍事物流保障網絡仿真與抗毀性測度研究[J].中國物流與采購,2015(1):74-75.

[2]史進.電力系統復雜網絡特性分析與模型改進[J].中國電機工程學報,2008,28(25):93-98.

[3]WATTSDJ,STRPGATZSH.CollectiveDynamicsof“Small-world”Networks[J].Nature,1998,393(5):440-442.

[4]BARABASIAL,ALBERTR.EmergenceofScalinginRandomNetwork[J].Science,1999,286(12):509-512.

[5]譚躍進,呂欣,吳俊,等.復雜網絡抗毀性研究若干問題的思考[J].系統工程理論與實踐,2008(6):116-200.

[6]王斌,譚東風,凌云翔.基于復雜網絡的作戰描述模型研究[J].指揮控制與仿真,2007,29(4):12-16.

[7]丁琳,譚敏生,肖煒.復雜網絡抗毀性研究綜述[J].電腦知識與技術,2009,5(1):51-53,61.

[8]邱原,邢煥革.基于復雜理論的作戰網絡關鍵邊評估方法[J].兵工自動化,2005,30(8):22-25.

[9]張勇,楊宏偉,白勇,等.基于復雜網絡理論的裝備保障網絡實證研究[J].裝備學院學報,2014,25(1):83-87.

[10]吳俊.復雜網絡拓撲結構抗毀性研究[D].長沙:國防科學技術大學,2008.

(責任編輯唐定國)

【后勤保障與裝備管理】

Analysis of Survivability of Warship Equipment Support Network

ZHANG Xiao, DAI Ming-qiang, SHAO Shuai

(Naval University of Engineering, Wuhan, 430033, China)

Abstract:Warship equipment support is an important part of the naval logistic support. Research on scientific warship logistic network construction has important significance to improve the efficiency of logistic and equipment support. To ensure a wide range of network nodes and complex lines, a security network model based on complex network theory was constructed. We designed the topology characteristic parameters of the network. Theoretical analysis and experimental results show that, the network survivability for random attack is better than selective attack, and attacking node is more meaningful for network survivability than attacking line. The docks which have more survivable interconnection paths have a higher contribution on the anti-destroying ability of the whole network.

Key words:warship equipment support; complex network theory; survivability

文章編號：1006-0707(2016)01-0097-05

中圖分類號：E239.3

文獻標識碼：A

doi:10.11809/scbgxb2016.01.023

作者簡介：張肖(1987—)，男，碩士研究生，主要從事軍事系統建模與運籌決策研究。

基金項目：全軍軍事學研究生資助項目(2012JY002-476)

收稿日期：2015-06-22；修回日期：2015-07-28