錐度球頭立銑刀磨削加工數學模型研究*

夏文勝，趙先鋒，高　飛，周兆鋒

(1.鹽城工學院 機械工程學院，江蘇 鹽城　224051；2.貴州大學 機械工程學院，貴陽　550025)

?

錐度球頭立銑刀磨削加工數學模型研究*

夏文勝1，趙先鋒2，高飛1，周兆鋒1

(1.鹽城工學院 機械工程學院，江蘇 鹽城224051；2.貴州大學 機械工程學院，貴陽550025)

摘要：針對錐度球頭立銑刀的幾何特征，根據錐度球頭立銑刀的成型原理，利用微分幾何的基本原理，研究了錐度球頭立銑刀前后刀面的刀刃曲線建模方法，設計了一種新的錐度球頭立銑刀刀刃曲線，并借助Visual Basic語言，利用SolidWorks軟件對所設計的刀刃曲線進行了建模和驗證。為錐度球頭類刀具的進一步設計提供了理論方法和依據。

關鍵詞：錐度球頭立銑刀；磨削加工；前后刀面；數學模型

0引言

合理的刀具數學模型是加工制造刀具研究的基礎。錐度球頭立銑刀制造的關鍵技術在于球頭部分的加工。錐度球頭立銑刀的切削性能與球刃的S形密切相關，較好的S形刃和合理的幾何參數分布是錐度球頭立銑刀切削性能的保證，如何獲得較好的S形刃和合理的幾何參數分布是錐度球頭立銑刀制造的關鍵。在現有的研究中，錐度球頭立銑刀球刃模型大多采用的球刃曲線是正交螺旋面和球面的交線[1-2]。我們在研究圓柱球頭立銑刀的制造過程中提出了新的前刀面數學模型[3]，并將其拓展為錐度球頭立銑刀的數學模型，利用這種建模方法加工出來的錐度球頭立銑刀，球頭與錐刃的螺旋槽槽底刀刃曲線能夠實現光滑連接。

1錐銑刀前刀面數學模型

1.1球刃前刀面數學模型

1.1.1球刃前刀面成形原理

我們提出了新的前刀面數學模型，其磨削運動關系由沿X、Y、Z三個方向的平移運動和繞銑刀軸線的旋轉運動構成。錐度球頭立銑刀前刀面磨削加工過程中砂輪與銑刀的位置關系如圖1所示。

圖1　錐銑刀前刀面磨削運動關系圖

BBe為錐度球頭立銑刀前刀面的槽底曲線，砂輪與工件發生相對運動時砂輪大圓圓周p0ppe始終與槽底曲線BBe相切，在工件上形成螺旋槽前刀面。在前刀面磨削加工過程中，從砂輪較大圓的端面圓周開始與槽底曲線的起點B相切開始，直至砂輪較大圓的端面最低點pe與槽底曲線的終點Be相切結束。由于螺旋槽的側面點的螺旋升角各不相同，螺旋槽側表面是扭曲的。為了避免砂輪與工件螺旋槽發生干涉甚至產生過切，安裝角∑1應比螺旋角β大1°～3°，則：∑1=β+(1°~3°)。為了使本磨削加工方法更具有通用性，將砂輪圓周端面繞砂輪大圓面上水平軸轉動∑2角度。為此建立以下三個坐標系(見圖1)：

工件坐標系σ=[O;X,Y,Z]：以錐度球頭立銑刀球頭的球心為坐標原點O；

砂輪坐標系σS=[OS;XS,YS,ZS]：OS在砂輪大圓的圓心，OSXSZS在砂輪大圓面內，YS垂直OSXSZS。

機床坐標系σ0=[O0;X0,Y0,Z0]：為了計算方便，假設機床坐標系σ0與工件坐標系σ的初始位置重合，坐標原點在錐度球頭立銑刀的球心O位置。

1.1.2球刃前刀面數學模型

錐度球頭立銑刀的槽底曲線在XZ平面上為橢圓線：[srcosθ,0,sr(1-c)sinθ]，在空間為橢球體螺旋線：[srcosθ,sr(1-c)sinθsinω,sr(1-c)sinθcosω]。

其中：c—槽深系數

sr—球頭半徑

ω—錐銑刀繞X軸轉動角度，且0°≤ω≤90°

θ—與X軸夾角0°≤θ≤90°θ=θ0t(θ0為轉動的角速度)

即在坐標系內，球頭部分的槽底曲線為：

(1)

又空間曲線為等螺旋角[3]：

(2)

其中：β—螺旋線的螺旋升角

p—為導程

可得

p=2πsr(1-c)tanβ

(3)

在砂輪坐標系下，砂輪的平面(大圓面)方程：

(4)

砂輪的平面法線方程為：

(5)

砂輪在固定坐標系下起始位置：

砂輪要繞X軸旋轉∑2，繞Z軸旋轉∑1，然后在Y方向平移距離為rsin∑1，在X方向平移距離為(sr+r)坐標變換過程為：

①繞X軸旋轉∑2

②繞Z軸旋轉∑1

③Y方向平移距離為rsin∑1

④X方向平移距離為(sr+rcos∑1)

變換矩陣分別為：

繞X軸旋轉∑2

(6)

繞Z軸旋轉∑1

(7)

Y方向平移矩陣(Y負方向)

(8)

X方向平移矩陣

(9)

可得變換矩陣為：

T=TrxTrzTtyTtx

(10)

即：

(11)

砂輪的平面方程在固定坐標系下起始位置為：

rcosηsin∑1-rsinηsin∑2cos∑1-rsin∑1

rsinηcos∑21]

(12)

即：

(13)

法線方程在固定坐標系下起始位置為：

(14)

-rcos∑2cos∑1+rsin∑-rsin∑21|

(15)

即：

(16)

下面求θ與η的關系：

槽底曲線旋轉到XOZ平面，可得：

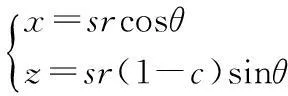
(17)

砂輪輪廓曲線投影到XOZ平面：

(18)

槽底曲線的切率：

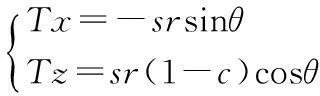
(19)

砂輪輪廓曲線切率：

(20)

兩者相切：

(21)

推導出θ與η的關系：

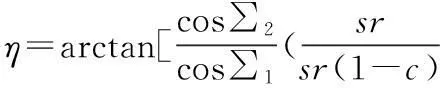
(22)

而θ與ω的關系：

(23)

砂輪大圓面方程：

(24)

砂輪繞X軸旋轉ω，其包絡面為：

(25)

(26)

整理得前刀面的方程：

(27)

即

(28)

1.2周刃前刀面數學模型

1.2.1周刃前刀面成形原理

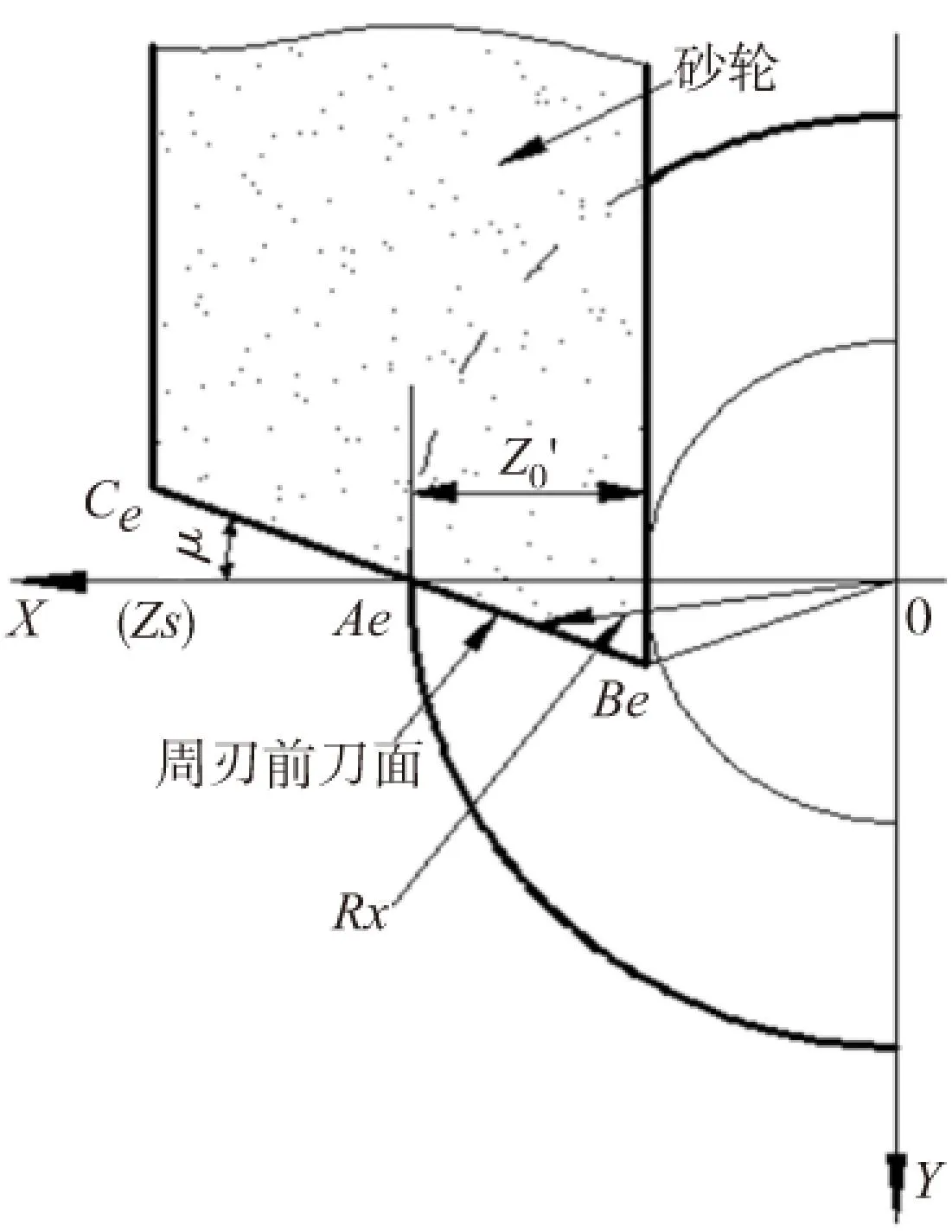
圖2　周刃前刀面的數學模型

球刃前刀面按上述方法形成后，B點到達Be點，即形成母線BC到達圖2所示位置。砂輪相對于銑刀作螺旋運動和軸向移動同時，砂輪還有一個遠離刀具軸線的運動，這樣，在工件上形成的螺旋槽，就由砂輪與工件接觸弧長的那一部分圓周產生[3-4]。在錐度球頭立銑刀制造過程中一次性依次完成球刃和周刃的加工，因此在磨削加工完球刃后，砂輪相對于工件作螺旋運動，周刃前刀面就是砂輪母線運動的包絡面。

1.2.2周刃前刀面數學模型

圓錐螺旋部分的槽底曲線，根據《數學在刀具設計中的應用》[5]，實際是圓錐螺旋線，為：

(29)

其中：β為螺旋線的螺旋升角

根據成形原理，可以推導出周刃前刀面的數學表達式。推導過程與球刃前刀面的推導過程相似，這里不再重復敘述。只給出推導結果，即周刃前刀面的數學表達式為：

(30)

式中m0—被加工螺旋槽部分的角度;

Rz—周刃前刀面上任一點的半徑，其計算公式為：

(31)

其中μ為砂輪母線與砂輪軸線的夾角，即圓錐砂輪的半錐度。

2錐銑刀后刀面的數學模型

2.1后刀面磨削加工滿足的條件

錐度球頭立銑刀后刀面與直柄球頭立銑刀相比，同樣包括球刃后刀面和周刃后刀面，球頭刀刃的形成是由球刃后刀面決定的。因此，加工球刃后刀面時，有兩個需要注意的地方。

(1)必須確保刀具的切削刃不能遭到任何破壞。在磨削加工錐銑刀后刀面的過程中，要盡量避免砂輪與球刃間的干涉，不偏離也不能過切。因此在磨削加工過程中，為了保證切削刃沒有遭到破壞，砂輪母線上始終要有一點與球刃相切觸。

(2)要求按等主后角來磨削加工。錐度球頭立銑刀刀齒的使用壽命，也就是錐銑刀刀赤的切削性能和磨損程度，是由球刃主后角來決定的。同時，從加工的角度來說，為了在加工過程中減小銑刀的振動，后刀面的加工要求按等后角來磨削。但是，由于錐銑刀球刃上各點的刃傾角各不相同，而且大多數情況下，按等法向后角來調整砂輪的位置，因此在球刃后刀面的磨削加工過程中會導致球刃各點的主后角不同[6]。

2.2球刃后刀面的磨削加工方法與數學模型

2.2.1后刀面的磨削加工方法

圖3　后刀面的成形運動

根據前刀面的成形原理，銑刀以角速度ω1繞回轉中心公轉，同時以K1ω1自轉。為了滿足后角的要求，砂輪軸線與銑刀軸線之間存在一個高度差h。在磨削加工過程中，銑刀繞球頭球心O以角速度ω2公轉，同時繞自身軸線以K2ω2轉動，如圖3所示。為了保證已經形成的刃口不被破壞，ω1與ω2，K1ω1與應滿足ω2=f1(ω1)，K2=f2(K1)。根據上述成型原理，建立銑刀后刀面數學模型。

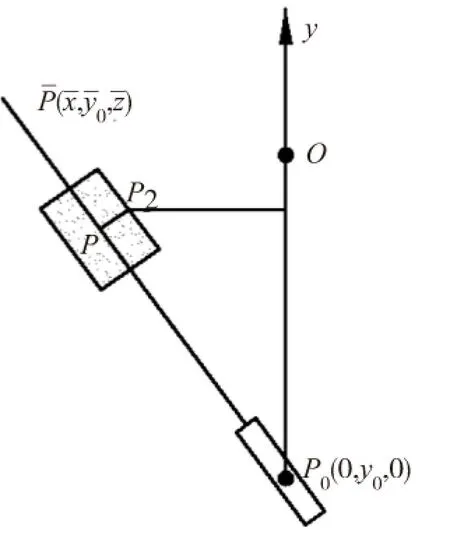
圖4　后刀面的加工原理

2.2.2后刀面數學模型—等主后角磨削加工

(1)重要曲線——曲線的法向等距線

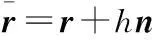
(32)

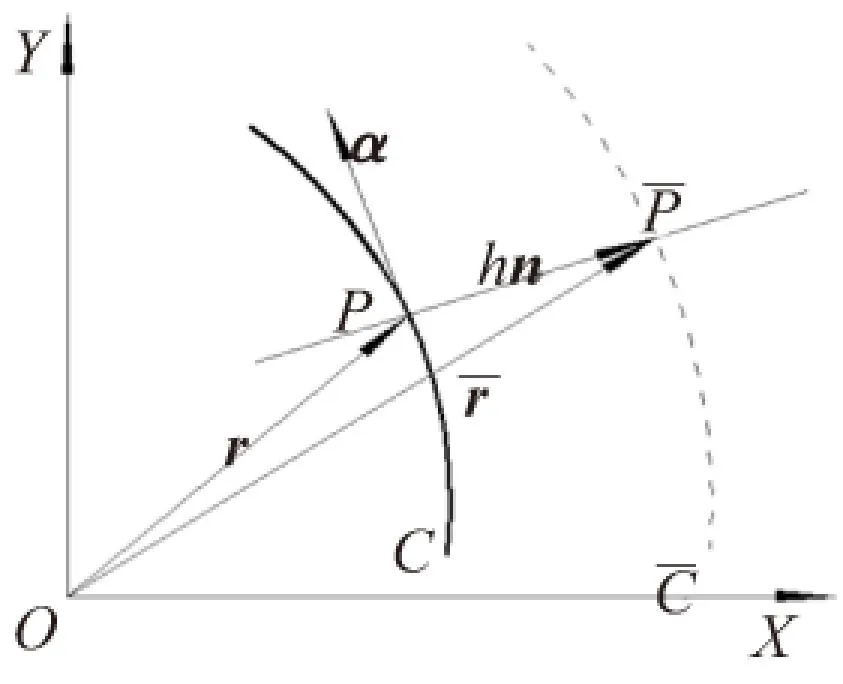
圖5　曲線的法向等距線

對于空間曲線上任意一點的法向矢量不是唯一的，因此其法向等距線也不唯一，但是我們知道空間曲線上任意一點法向矢量n可以根據該點的唯一幺切矢α0和主幺法矢n0獲得，為此引入如下定理：

(2)一個重要定理

矢量旋轉定理[9]：空間坐標系中，一個矢量n0繞另一矢量α0旋轉αn角后，所得到的新矢量n可以表示為：

n=n0cosαn-(α×n0)sinαn

(33)

下面結合后刀面的磨削條件，賦予上述定義及定理的物理意義。

(3)后刀面的數學模型

后刀面磨削加工的數學模型，如圖6所示，設砂輪母線上一點要與S形刃相切并且相接觸，并且保持砂輪軸線和切點處的切線矢量平行，切點處銑刀應具有已知的法向后角αn,，滿足這些條件的砂輪中心軌跡必為S形刃的一條法向等距線。如圖7所示，設坐標系為加工前刀面坐標系σ=[O;X,Y,Z]，在S刃上取任意點p，設砂輪的半徑為R1，在p點相切，則p點S刃的法向等距線方程為：

r1=r+R1r0

(34)

圖6　后刀面的數學模型

圖7　S刃的法向等距線

幺法矢r0可由切點p處球面主幺法矢N1繞該點處端刃切幺矢T0旋轉αn求得：

r0=N1cosαn-(T0×N1)sinαn

(35)

下面求p點端刃切幺矢T0：

如圖8所示，設p(X,Y,Z)為錐度球頭立銑刀球刃主切削刃所求點的坐標，則球面上該點處的單位法矢N1為：

(36)

圖8　法前角示意圖

球頭前刀面在該點的法矢N2為：

(37)

球刃主切削刃上在該點(X,Y,Z)的切矢T1=N1×N2，即：

T1=(N1YN2Z-N2YN1Z)i+(N1ZN2X-N2ZN1X)j+

(N1XN2Y-N2XN1Y)k

(38)

而

(39)

由于是等主后角磨削加工，給定的是主后角α0，根據《金屬切削原理》[10]求出法向后角αn。

ctgαn=ctgα0×cosλs

(40)

聯系式(34)、(35)、(39)、(40)可得到S形球刃的法向等距線方程，由于以上求導過程和矢量運算比較復雜，本文只給出其表達式。

r1=

(41)

3磨削仿真加工實例

3.1前刀面的磨削仿真加工

依據實際加工過程，以SolidWorks為操作平臺，VB為開發工具，建立錐度球頭立銑刀磨削仿真加工系統。此虛擬加工系統充分利用SolidWorksApI的方法與屬性，選用直接實體造型法來實現復雜曲面仿真加工。

按照錐度球頭立銑刀前刀面形成的位置關系編制合理的運動程序，用程序控制砂輪的各種運動，通過實體間的布爾差運算來實現砂輪實體對銑刀毛坯實體的切除加工，從而形成球刃與周刃前刀面，前刀面的仿真結果如圖9所示。可以看出：錐度球頭立銑刀的球刃為S形弧形刃，刃形曲線較為理想；球刃前刀面與周刃前刀面能實現光滑連接。

(a)S形刃　　　　　(b)S形刃在球頭和圓錐結合處

3.2后刀面的磨削仿真加工

利用前刀面磨削仿真加工的結果來實現后刀面的磨削仿真加工。按照磨削錐度球頭立銑刀前刀面形成的位置關系，通過程序選出所有主切削上的點，根據這些被選中的點，編制合理的運動程序，同樣利用程序控制砂輪的移動和偏轉，通過實體間的布爾差運算，實現砂輪實體對銑刀毛坯實體的切除加工，從而形成球刃后刀面和周刃后刀面，如圖10所示。

(a)球刃后刀面　　　　　(b)周刃后刀面

4結束語

本文以錐度球頭立銑刀的正交螺旋形的刀刃曲線為基礎，根據錐度球頭立銑刀前后刀面的成形原理，分別建立了錐度球頭立銑刀數學模型，他們具有等法向前角的前刀面、等主后角的后刀面。最后利用該模型建立了錐度球頭立銑刀磨削加工仿真與分析系統，以檢驗模型的正確性。該模型及其仿真設計軟件為錐度球頭立銑刀的設計、制造與進一步開發提供了理論方法與基礎。

[參考文獻]

[1] 盛尚雄,吳卓,馬世輝. S 形刃球頭立銑刀的數學模型[J]. 甘肅科學學報, 2009,21(4): 104-108.

[2] 李清,王太勇,吉洪武. 基于物理仿真模型的螺旋立銑刀建模[J]. 組合機床與自動化加工技術,2005(8):19-22.

[3] 李帥. 新型球頭立銑刀前刀面刃磨仿真研究[D]. 貴州:貴州大學,2008.

[4] 康長玉,朱斌,雷君相. 利用數控改造加工等螺旋角等前角錐球頭立銑刀[J]. 制造技術與機床, 2010(6): 129-131.

[5] 姚南珣. 數學在刀具設計中的應用[M]. 北京:機械工業出版社,1986.

[6] 韓政峰. 基于四軸磨削加工的球頭立銑刀數學模型研究[D]. 貴州:貴州大學, 2008.

[7] 唐余勇，汪興濤，鮑青山. 非數控加工球頭銑刀的主干數學模型[J]. 工具技術,2002,36 (3):19-21.

[8] 黃宣國. 空間解析幾何與微分幾何[M]. 上海:復旦大學出版社,2003.

[9] 吳叢炘,唐余勇. 微分幾何講義[M].北京:高等教育出版社,1985.

[10] 陸劍中，孫家寧.金屬切削原理與刀具[M]. 5版.北京:機械工業出版社,2011.

(編輯李秀敏)

Research on Grinding Mathematical Models of the Taper Ball-nose End Milling Cutter

XIA Wen-sheng1, ZHAO Xian-feng2, GAO Fei1, ZHOU Zhao-feng1

(1.School of Mechanical Engineering, Yancheng Institute of Technology, Yancheng Jiangsu 224051,China; 2. School of Mechanical Engineering, Guizhou University, Guiyang 550025, China)

Abstract：For geometrical features of taper ball-nose end milling cutter, according to the forming principle of taper ball-nose end milling cutter, with the basic principles of differential geometry, the modeling method for edge curves of taper ball-nose end milling cutter was studied and a novel edge curve of taper ball-nose end milling cutter was designed. Beside，with the Visual Basic language, the edge curve which designed was modeled and verified by using SolidWorks. As a result, a theoretical method and basis for the further design of taper ball-nose end milling cutter was provided.

Key words：taper ball-nose end milling cutter; grinding ; rake and flank; mathematical model

中圖分類號：TH162;TG506

文獻標識碼：A

作者簡介：夏文勝(1984—)，男，江蘇阜寧人，鹽城工學院講師，工學碩士，從事機床、刀具與模具方面的教學科研工作，( E-mail)xws2222@126.com。

*基金項目：貴州省科技廳重點科技項目：高性能球頭立銑刀工具磨的研制[黔科合GZ字(2007)3008]

收稿日期：2014-10-24；修回日期：2014-11-27

文章編號：1001-2265(2016)01-0122-05

DOI:10.13462/j.cnki.mmtamt.2016.01.034