機床熱誤差建模技術研究及試驗驗證*

李泳耀，叢　明，廖忠情，孫宗余，李宏坤

(1. 大連新宇理工科技開發中心有限公司，遼寧 大連　116024;2. 大連理工大學 機械工程學院，遼寧 大連　116023;3. 一汽解放汽車有限公司無錫柴油機廠，江蘇 無錫　214026)

?

機床熱誤差建模技術研究及試驗驗證*

李泳耀1，2，叢明1，2，廖忠情1，2，孫宗余3，李宏坤1，2

(1. 大連新宇理工科技開發中心有限公司，遼寧 大連116024;2. 大連理工大學 機械工程學院，遼寧 大連116023;3. 一汽解放汽車有限公司無錫柴油機廠，江蘇 無錫214026)

摘要：針對機床熱誤差補償技術中預測模型建立的問題，綜合多元線性回歸及Bp神經網絡的優點，提出一種機床熱誤差建模新方法。由不同樣本數據建立若干多元線性回歸模型，依據統計學理論篩選出預測精度及魯棒性高的回歸模型，預處理后將其結果輸入到Bp神經網絡中進行非線性擬合建模，在不斷調節網絡權值及對神經網絡訓練的基礎上，最終建立熱誤差補償模型。在臥式加工中心上進行試驗驗證，主軸Z向最大熱誤差從17.895μm減小到1.654μm。

關鍵詞：熱誤差模型；多元線性回歸；統計學；Bp神經網絡

0引言

機床熱誤差是由其零部件間因溫升變化而導致不同程度的熱變形引起的，最終會反映到刀具和工件上，引起其相對位置的偏移，降低機床的加工精度[1]。大量研究表明，熱誤差占機床總誤差的比例往往在40%~80%，越是精密的機床，所占比例越大[2-3]。熱誤差補償技術是一種有效提高機床加工精度的方法[4]，而實現熱誤差補償的前提是進行機床溫度測點優化及熱誤差建模。

近年來，國內外學者對熱誤差建模技術進行了大量研究，提出了許多理論和方法，如多元線性回歸法[5]，人工神經網絡法[6-7]，時間序列分析法[8]，最小二乘支持向量機法[9]，灰色理論法[10]等。由于機床熱誤差是一個典型的非線性系統，這些單一的建模方法雖然取得了成功，但其補償精度及魯棒性均有待進一步提高。結合每種理論的優點，也有學者提出了多種理論相結合的方法，如灰色神經網絡法[11-12]，時序分析及灰色理論法[13]，人體免疫神經網絡法[14]等，這些方法綜合了每種理論的優點，將兩種模型的預測結果進行有效的組合，充分利用其預測信息，提高了模型的預測能力。

就單一模型而言，多元線性回歸模型簡單，容易計算，但缺乏自主學習能力及誤差反饋調節機制，模型預測的精確性及魯棒性得不到保證。Bp神經網絡屬前饋式網絡模型，是一種廣泛使用且較為復雜的神經網絡[7]，不僅包括輸入、輸出節點，還有一層或多層隱層，可以獲得很高的預測精度，但模型收斂速度慢，模型訓練時間長，容易出現局部極值，不適于工作條件變化較大的場合。綜合兩者的優缺點，本文采用多元線性回歸及Bp神經網絡相結合的方法來實現機床熱誤差建模，基本思想是：首先采用多元線性回歸對測點數據預處理，然后由Bp神經網絡進行綜合計算及誤差反饋，以提高模型預測精度及魯棒性。

1模型的理論分析及建立

1.1多元線性回歸

多元線性回歸建模方法采用統計學理論建立多輸入、單輸出關系的模型。就本文熱誤差建模而言，溫度變量為多輸入，機床某一方向上的熱誤差為單輸出。以Z向為例，熱誤差模型一般形式可表示為：

ΔZ=β0+β1ΔT1+β2ΔT2+…+βpΔTp

(1)

式中，ΔZ為Z向熱誤差變化量，ΔTi(i=1,2,…,p)為各測點溫度變化量，βi(i=0,1,…,p)為回歸系數，ε為隨機誤差。

假設通過試驗獲取N組觀測數據：(Ti1,Ti2,…,Tip;Zi)，則模型可表示為：

ΔZ=ΔTβ+ε

(2)

式中，

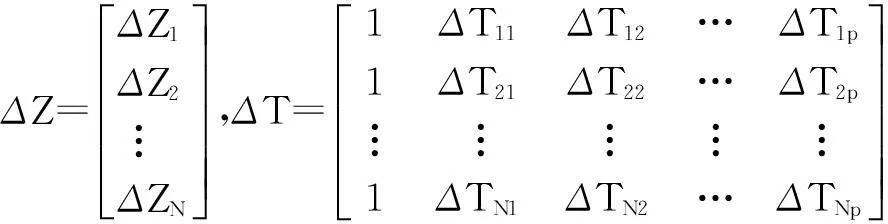
采用最小二乘法計算出回歸系數βi的理論估計值。設bi(i=0,1,…,p)為參數βi的最小二乘估計，則bi應使得ΔZi的殘差平方和最小，即使得：

(3)

達到最小。

要使Q(b0，b1，…，bp)達到最小，則需滿足：

(4)

模型建立后，采用統計學理論對模型參數進行評價，如對回歸系數、回歸模型等進行顯著性檢驗，通過檢驗的模型方可用于熱誤差預測。

1.2Bp神經網絡

Bp神經網絡具有非線性映射的特點，以及良好的數據并行處理、數據容錯、存儲等能力，并能實時反饋并校正輸出誤差[11]。其建立的一般步驟為：

(1)數據的準備

本文采用的是多輸入、單輸出的網絡結構。輸出層的傳遞函數為線性函數，輸入層、隱藏層的傳遞函數為Sigmoid函數，表達式為：

(5)

其值域為[0, 1]。輸入變量的取值范圍亦要求為[0, 1]，否則不同數量級的輸入變量值將直接影響到網絡權值的確定及最終的預測結果。通常采用極差法對輸入變量進行標準化處理，即：

(6)

其中，xmax和xmin分別為輸入變量的最大值和最小值。

(2)網絡結構的確定

網絡結構的復雜度(預測精度)與模型收斂速度反相關，應在兩者間做出權衡。而決定神經網絡復雜度的是隱藏層層數及其隱節點個數。在保證預測精度的前提下，通常選擇一個隱層的網絡最合算。隱節點的選取沒有確定的準則，通常隱節點越多模型越易收斂，但可能會產生模型過擬合問題，應根據模型實際訓練情況進行選取。

(3)網絡權值的確定

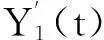
(7)

網絡權值調整的目標是使預測誤差Ej(t)最小，采用梯度下降法可以實現。則第個i節點對輸出節點的權值調整量為：

(8)

其中，負號表示負梯度方向，η為學習率。

那么，t+1時刻節點的權值調整為：

Wij(t+1)=α·Wij(t)+ΔWij

(9)

其中，α通常為常數。

一般是初始隨機給定一網絡權值(通常來自均值為0，取值范圍[-0.5，0.5]間的正態分布)，根據上述原理反復調整權值，直至誤差達到一個較理想值為止。這樣，網絡權值便被確定下來。

1.3預測模型的建立

對于同一組建模數列，采用不同樣本數據建立的模型不盡相同，且模型預測精度亦存在差別。為獲得最佳預測效果，建立多元線性回歸-Bp神經網絡熱誤差預測模型，如圖1所示。首先采用多元線性回歸模型對關鍵溫度測點及熱誤差數據進行第1次預處理，根據樣本劃分不同，建立多個回歸模型；其次對回歸模型2次預處理，根據統計學理論篩選出若干預測效果較好的模型；然后將其預測結果輸入到Bp神經網絡中進行非線性擬合建模，在這個過程中需要不斷對神經網絡進行訓練，不斷調節網絡權值；最終建立熱誤差預測模型。

圖1　預測模型結構圖

就預測模型中的Bp神經網絡模塊來講，輸入層為第2次預處理后的多元線性回歸模型的預測值，輸出層則為最終的熱誤差預測值，很好的解決了Bp神經網絡不適于工作條件變化較大場合的問題，亦有利于發揮其非線性映射及誤差反向傳播學習的特點。

2試驗驗證及結果分析

2.1試驗分析

試驗在某臥式加工中心上進行，采用電渦流位移傳感器測量主軸Z向熱誤差(圖2)，在經過溫度測點優化后的四個關鍵位置上布置溫度傳感器，分別為：X向電機表面ΔT4，主軸中外環面ΔT6，環境溫度ΔT10，X向遠機端軸承座表面ΔT12，如圖3所示。試驗采用空切削方式及階梯轉速，盡量模擬實際加工過程，共進行3小時的數據采集，如圖4、圖5所示。

圖2　Z向位移傳感器布置圖

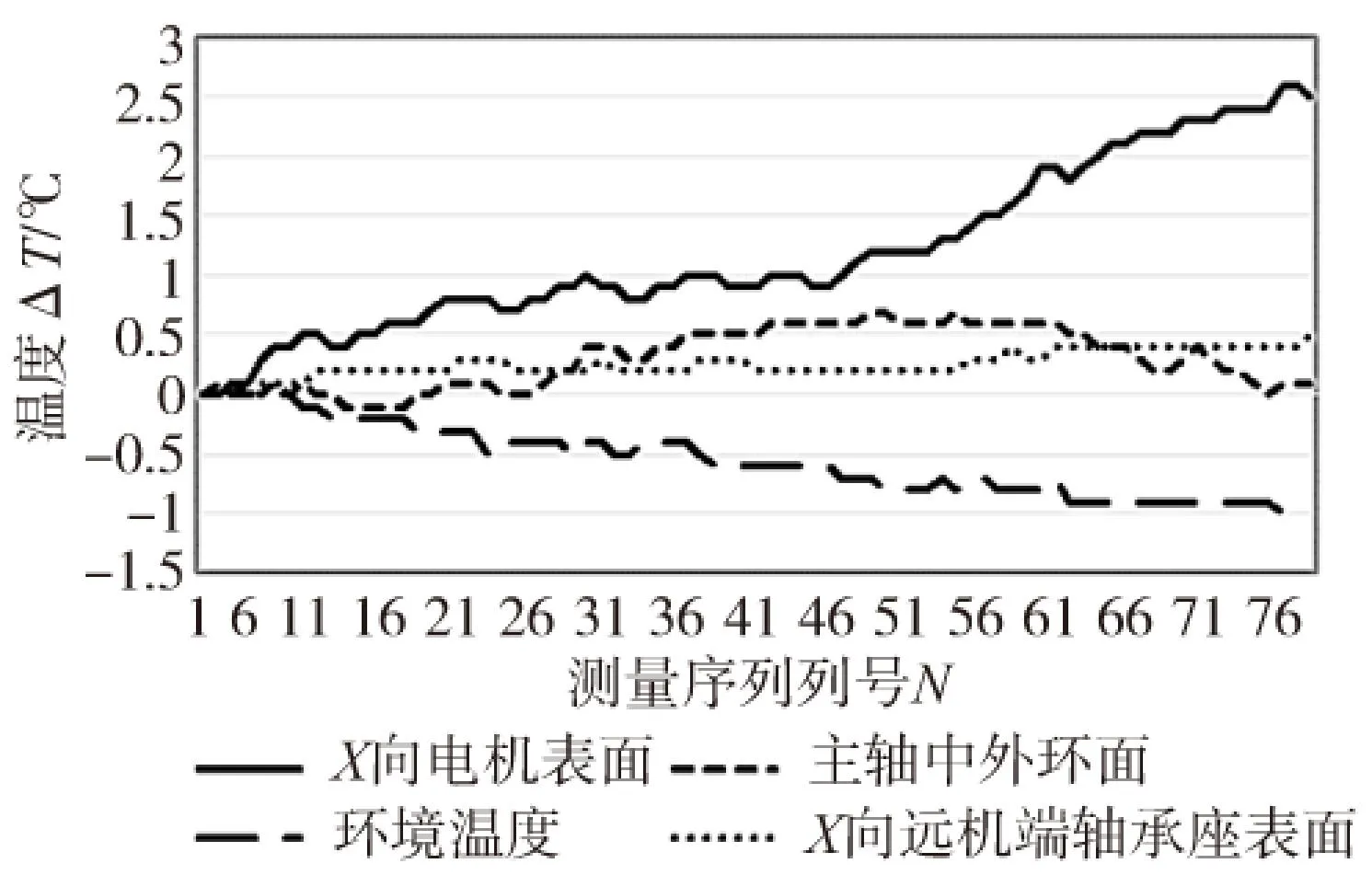
圖4　關鍵溫度測點數據

圖5　Z向熱誤差

2.2模型的建立

根據關鍵溫度測點及Z向熱誤差數據，首先建立多元線性回歸模型。隨機對試驗數據進行劃分(70%用于訓練，30%用于測試)，共進行十次劃分。根據每次用于建模數據的不同，共建立十組回歸模型，并對模型進行基于統計學原理的分析，如表1所示。

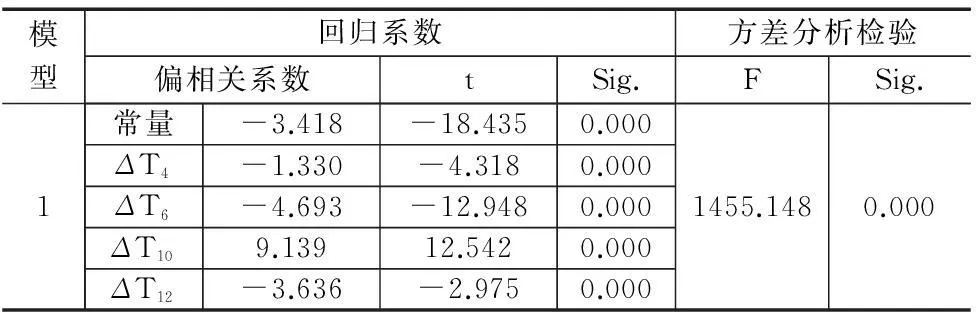
表1　多元線性回歸模型分析

續表

注：此處的殘差均取了絕對值，下同。

下面根據一定規則，篩選出預測精度及魯棒性均較高的五個模型。

(1)對回歸系數進行顯著性水平為0.01的t檢驗，可知模型8、9檢驗沒通過，排除。

(2)R為復相關系數，取值范圍[0,1]，表征自變量和因變量間線性回歸關系的密切程度，其值越大回歸關系越密切。調整的R2反映模型的擬合效果，其值越大說明擬合效果越好。剩余標準差(殘差的標準差)表征了模型預測結果的精確度，其值越小預測效果越好。模型摘要如圖6所示。根據以上規則，排除模型2。

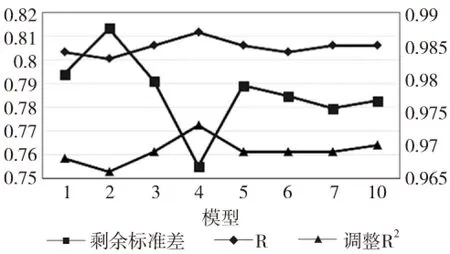
圖6　模型摘要

(3)殘差表征了模型預測值與實際值的差別程度，最大殘差則在一定程度上反映了模型的魯棒性。如圖7所示，模型4和5的前后訓練和測試的預測值的最大殘差差別較大，且模型5的魯棒性更差些，這里先排除掉模型5。

(4)平均殘差反映了模型的整體預測精度，如圖8所示。模型4的訓練和測試預測值的平均殘差差別較大，且測試預測值的平均殘差要遠高于其他模型，排除模型4。

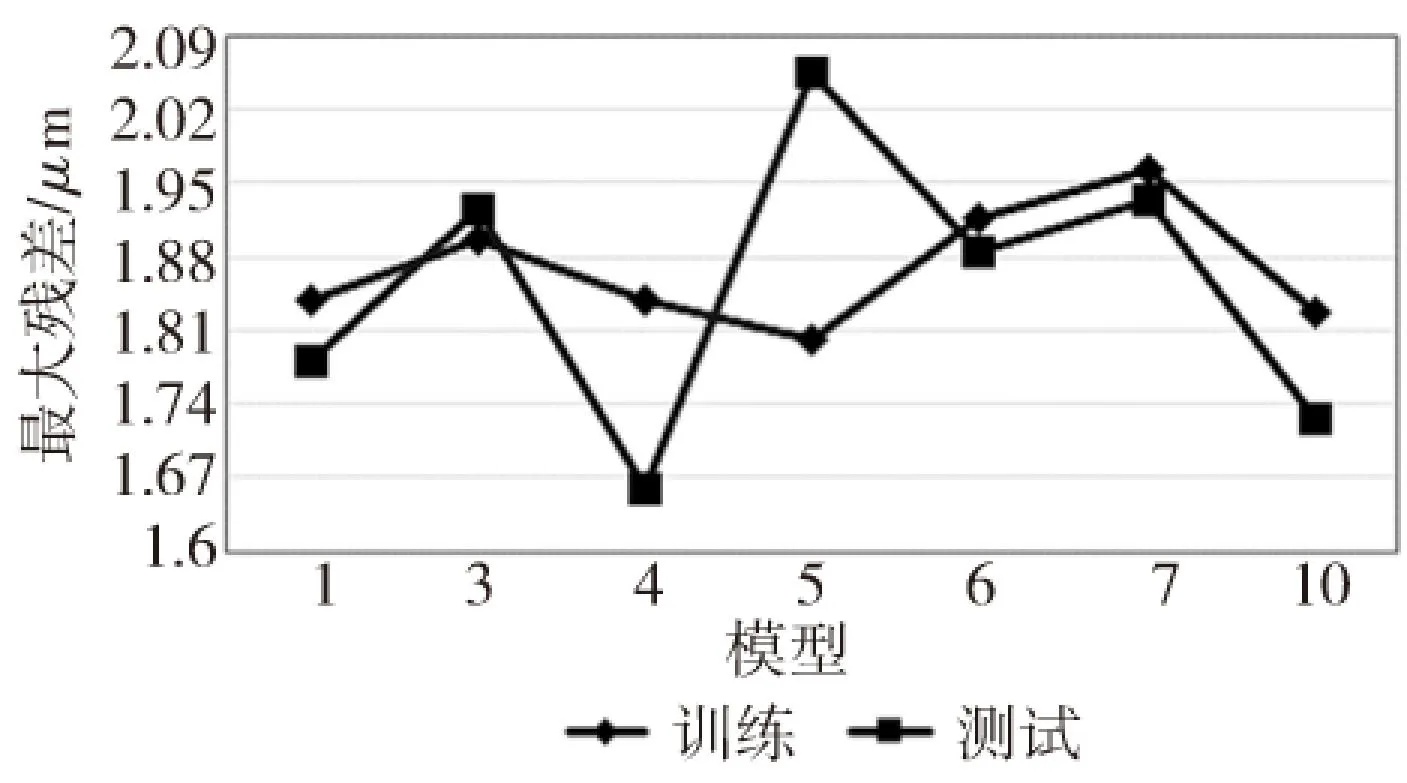
圖7　模型最大殘差

圖8　模型平均殘差

通過以上分析，篩選出5個精度和魯棒性均較高的回歸模型：1、3、6、7、10。

2.3結果驗證

Bp神經網絡預測模型采用5-8-1的拓撲結構，即輸入層有5個節點，隱藏層有8個節點，輸出層有1個節點，設置學習速率。以篩選出的五個模型的預測值作為輸入，建立Bp神經網絡預測模型(記為模型A)，如圖9所示。

若不采用本文方法，直接建立多元線性回歸模型(記為模型B)或Bp神經網絡模型(記為模型C)，其誤差預測如圖10、圖11所示。

圖9　模型A的預測圖

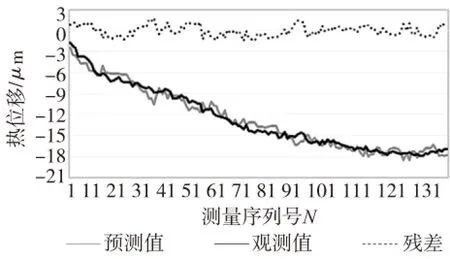
圖10　模型B的預測圖

圖11　模型C的預測圖

對比3種方法的熱誤差模型預測精度，結果如表2所示。

由表2可知，采用本文方法建立的模型，其最大殘差僅為1.654μm，平均殘差亦只有0.557μm，預測效果優于其他兩種方法， 且殘差基本分布于零軸附近，波動幅值均小于其他兩種模型。

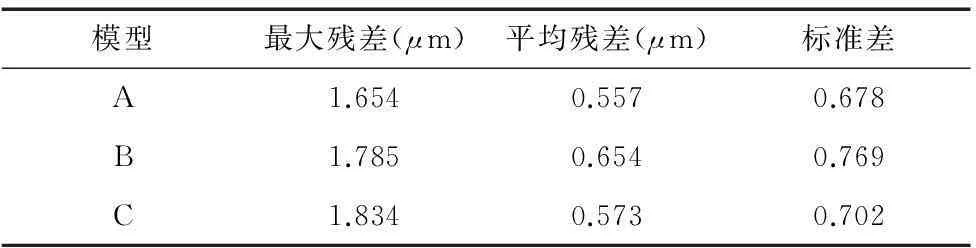
表2　熱誤差模型預測結果比較

3結論

(1)采用本文方法對臥式加工中心進行熱誤差建模及試驗驗證，主軸Z向最大熱誤差從17.895μm減小到1.654μm，平均殘差僅為0.557μm，大幅提高了模型的預測精度。

(2)綜合多元線性回歸及Bp神經網絡的優點建立了新的熱誤差預測模型。相對于其他模型，該模型具有預測精度高、魯棒性好、對原始數據要求低等優點，適用于加工條件變化較大場合的機床熱誤差補償。

[參考文獻]

[1] Ramesh R, Mannan M A, poo A N. Error compensation in machine tools—a review part Ⅱ: thermal errors[J]. International Journal of Machine Tools & Manufacture, 2000, 40(9): 1257-1284.

[2] 凡志磊, 李中華, 楊建國. 基于偏相關分析的數控機床溫度布點優化及其熱誤差建模[J]. 中國機械工程, 2010, 21(17): 2025-2028.

[3] pahk H J, Lee S W. Thermal error measurement and real time compensation system for the CNC machine tools incorporating the spindle thermal error and the feed axis thermal error[J]. International Journal of Advanced Manufacture Technology, 2002, 20(7): 487-494.

[4] Yang J G, Yuan J X, NI J. Thermal error mode analysis and robust modeling for error compensation on a CNC turning center[J]. International Journal of Machine Tools & Manufacture, 1999, 39: 1367-1381.

[5] 楊建國, 任永強, 朱衛斌, 等．數控機床熱誤差補償模型在線修正方法研究[J]. 機械工程學報, 2003, 39(3): 81-84.

[6] Yang S, Yuan J, Ni J. The improvement of thermal error modeling and compensation on machine tools by CMAC neural network[J]. International Journal of Machine Tools and Manufacture, 1996, 36(4): 527-537.

[7] Mize C D, Ziegert J C. Neural network thermal error compensation of a machining center[J]. Journal of the International Societies for precision Engineering and Nanotechnology, 2000, 24(4): 338-346.

[8] 李永祥, 童恒超, 曹洪濤, 等. 數控機床熱誤差的時序分析法建模及其應用[J]. 四川大學學報, 2006, 38(2): 74-78.

[9] 林偉青, 傅建中, 陳子辰, 等. 數控機床熱誤差的動態自適應加權最小二乘支持矢量機建模方法[J]. 機械工程學報, 2009, 45(3): 178-182.

[10] 閆嘉鈺, 楊建國. 灰色GM(X, N)模型在數控機床熱誤差建模中的應用[J]. 中國機械工程, 2009, 20(11): 1297-1300.

[11] 張毅, 楊建國. 基于灰色理論預處理的神經網絡機床熱誤差建模[J]. 機械工程學報, 2011, 47(7): 134-139.

[12] 張毅, 楊建國. 基于灰色神經網絡的機床熱誤差建模[J]. 上海交通大學學報, 2011, 45(11): 1581-1586.

[13] 李永祥, 楊建國, 郭前建, 等. 數控機床熱誤差的混合預測模型及應用[J]. 上海交通大學學報, 2006,40(12): 2030-2033.

[14] 閆嘉鈺, 楊建國. 基于人體免疫系統RBF網絡的數控機床熱誤差建模[J]. 上海交通大學學報, 2009, 43(1): 148-152.

(編輯李秀敏)

An Modeling Method for Machine Tool Thermal Error and Experimental Verification

LI Yong-yao1,2,CONG Ming1,2, LIAO Zhong-qing1,2, SUN Zong-yu3, LI Hong-kun1,2

(1.Dalian Xinyu Science Technology Development Center CO.，LTD,Dalian Liaoning 116024，China；2. School of Mechanical Engineering,Dalian University of Technology，Dalian Liaoning 116023，China)

Abstract：A new method is proposed to build the thermal error compensation model considering the advantages of multiple linear regression and Bp neural network. Some multiple linear regression models are established by using different sample data. According to the statistics principle, some high accurate and robust models are selected. The predicted results are input into Bp neural network for nonlinear fitting modeling. The final thermal error compensation model is built on the basis of adjusting the network weights and training the neural network constantly. The method is validated on a horizontal machining center. The result shows that Z-axis thermal error is reduced from 17.895μm to 1.654μm.

Key words：thermal error model; multiple linear regression; statistics principle; Bp neural network

中圖分類號：TH161；TG65

文獻標識碼：A

作者簡介：李泳耀(1991—)，男，河南商丘人，大連理工大學碩士研究生，研究方向為機床精度穩定性分析，(E-mail)liyongyao1991@163.com。

*基金項目：大連市科技計劃項目“汽車發動機和柔性自動線可靠性技術研究”(2013A11GX012)；國家“高檔數控機床與基礎制造裝備”科技重大專項課題(2013ZX04012071)

收稿日期：2015-06-12

文章編號：1001-2265(2016)01-0063-04

DOI:10.13462/j.cnki.mmtamt.2016.01.018