基于THDMOpSO綠色減速器模塊劃分不確定優(yōu)化*

劉電霆，張全永

(桂林理工大學(xué) a.機(jī)械與控制工程學(xué)院；b.信息科學(xué)與工程學(xué)院，廣西 桂林　541004)

?

基于THDMOpSO綠色減速器模塊劃分不確定優(yōu)化*

劉電霆a，張全永b

(桂林理工大學(xué) a.機(jī)械與控制工程學(xué)院；b.信息科學(xué)與工程學(xué)院，廣西 桂林541004)

摘要：針對含不確定的變量或參數(shù)的多目標(biāo)問題，以減速器的模塊化綠色配置設(shè)計(jì)為例，引入?yún)^(qū)間數(shù)和模糊數(shù)作為變量，研究了綠色設(shè)計(jì)中包含不確定因素的產(chǎn)品模塊劃分問題，給出了模塊劃分的原則和主要步驟，以模塊內(nèi)部聚合度最大、模塊之間耦合度最小和模塊劃分所得綠色度最高為多目標(biāo)函數(shù)，建立了產(chǎn)品綠色模塊劃分的不確定優(yōu)化模型，對其中區(qū)間數(shù)和三角模糊數(shù)確定化后，提出THDMOpSO方法進(jìn)行求解，通過減速器結(jié)構(gòu)模塊構(gòu)造進(jìn)行驗(yàn)證，表明此方法具有可行性和生產(chǎn)實(shí)用價(jià)值。

關(guān)鍵詞：不確定優(yōu)化；綠色設(shè)計(jì)；模塊化設(shè)計(jì)；十進(jìn)制離散多目標(biāo)粒子群算法

0引言

在綠色設(shè)計(jì)[1-3]成為企業(yè)產(chǎn)品設(shè)計(jì)標(biāo)配的時(shí)代，綠色產(chǎn)品的模塊化設(shè)計(jì)迎合了現(xiàn)代化設(shè)計(jì)的理念，已經(jīng)開始從大批量生產(chǎn)向大規(guī)模定制轉(zhuǎn)變，各種綠色配置設(shè)計(jì)和組合設(shè)計(jì)正浮出水面。近年來，針對綠色模塊化設(shè)計(jì)問題的研究成為熱點(diǎn)，但在已有研究中很少有人考慮設(shè)計(jì)過程中的不確定性因素以及離散多進(jìn)制多目標(biāo)粒子群算法求解[4-11]。

本文基于現(xiàn)有減速器的綠色模塊劃分方法，并考慮其中存在的不確定因素和綠色設(shè)計(jì)等目標(biāo)，從建立不確定模型入手，引入pareto 集理念，提出一種十進(jìn)制多目標(biāo)離散粒子群方法，求解并驗(yàn)證所提出的方法的有效正確性，具有生產(chǎn)實(shí)用性。

1案例分析及建模

1.1問題的描述

在綠色設(shè)計(jì)中產(chǎn)品族模塊劃分的原則可簡記為：高內(nèi)聚低耦合。高內(nèi)聚指模塊內(nèi)部的聚合度盡量大即模塊內(nèi)部之間的關(guān)聯(lián)應(yīng)該盡量大；低耦合指模塊之間的耦合度盡量小即模塊之間的交互應(yīng)該盡量少；同時(shí)還應(yīng)該考慮其綠色性盡量達(dá)到最優(yōu)。以一個(gè)減速器為例，實(shí)際生產(chǎn)中減速器結(jié)構(gòu)分為五大模塊，共十個(gè)基本單元，通過功能相關(guān)性分析，把同一功能的基本單元盡量聚合成一個(gè)模塊，以提高模塊的功能獨(dú)立性。通過結(jié)構(gòu)相關(guān)性分析，盡量使結(jié)構(gòu)相關(guān)的劃在一個(gè)模塊以保證結(jié)構(gòu)的完整性。它們的相關(guān)性大小是一種定性問題，可用三角模糊數(shù)來描述。比如功能相關(guān)性從弱到強(qiáng)有屬性“無”，“一般”，“較強(qiáng)”，“強(qiáng)”，“極強(qiáng)”等特性，可用三角模糊數(shù)[0.0,0.0,0.0]，[0.0,0.2,0.4], [0.2,0.4,0.6], [0.4,0.6,0.8], [0.6,0.8,1]表示,同理可以進(jìn)行結(jié)構(gòu)相關(guān)性的表示，考慮到篇幅限制，這里不再累述。

在確定了功能和結(jié)構(gòu)的度量后，綠色設(shè)計(jì)中產(chǎn)品族模塊劃分時(shí)必然要有一些綠色準(zhǔn)則，本文設(shè)有回收性、維護(hù)性、升級性、重用性、處理性等5個(gè)準(zhǔn)則,對每個(gè)綠色準(zhǔn)則的度量可采用區(qū)間數(shù)值表示，如表3所示。

1.2相關(guān)數(shù)據(jù)建立

減速器結(jié)構(gòu)由聯(lián)軸器、潤滑、齒輪、軸、箱體、軸承、端蓋、密封、螺釘、鍵等10個(gè)基本單元組成。本文分別用T1、T2、T3、T4、T5、T6、T7、T8、T9、T10表示。其功能關(guān)聯(lián)矩陣和結(jié)構(gòu)關(guān)聯(lián)矩陣數(shù)值如表1和表2所示[12]。

表1　減速器功能關(guān)聯(lián)表

表2　減速器結(jié)構(gòu)關(guān)聯(lián)表

續(xù)表

考慮無量綱化后T1、T2、T3、T4、T5、T6、T7、T8、T9、T10的綠色屬性區(qū)間值見表3所示。

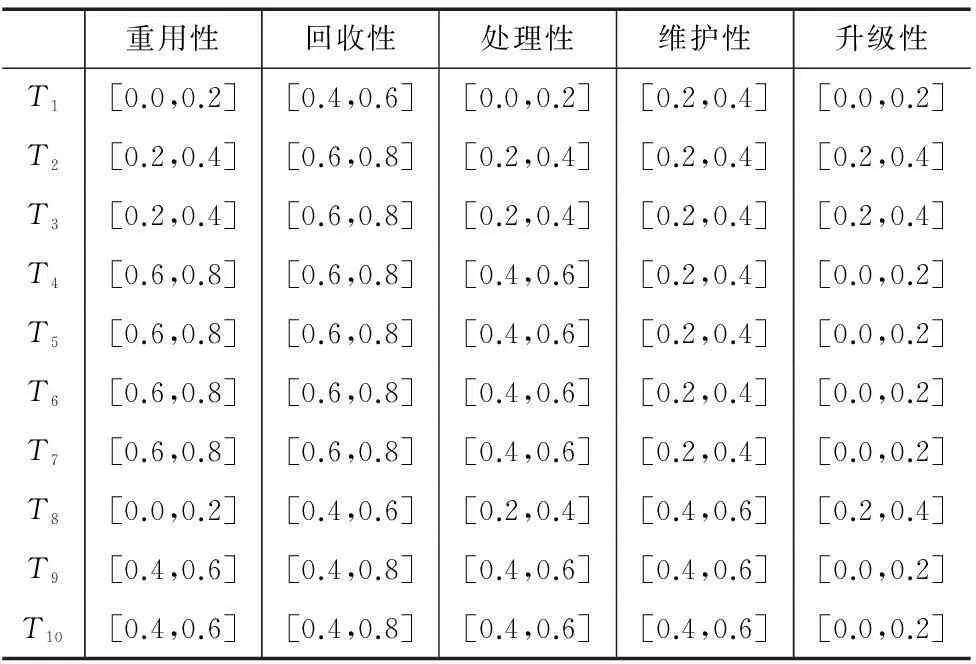
表3　綠色屬性區(qū)間值

2模塊劃分不確定模型

2.1耦合度和內(nèi)聚度以及綠色度模型

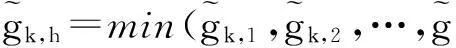
(1)

(2)

(3)

2.2三角模糊數(shù)的運(yùn)算法則

本文采用加權(quán)重心法對三角模糊數(shù)進(jìn)行確定化，即利用式(4)求得確定化數(shù)a：

(4)

2.3區(qū)間數(shù)的運(yùn)算法則:

區(qū)間數(shù)有其自身的二元運(yùn)算法則，同實(shí)數(shù)的二元運(yùn)算法則類似，設(shè)兩個(gè)區(qū)間數(shù)A=[aL,aR]和B=[bL,bR],令λ∈R,，則其對應(yīng)的二元運(yùn)算法則[15]如下。

(1)A-B=[aL-bL,aR-bR]

(2)λA=λ[aL,aR,]

(3)A+B=[aL+bL,aR+bR]

設(shè)帶區(qū)間數(shù)的目標(biāo)函數(shù)表示為Minf(X,U),則確定化轉(zhuǎn)化方法如式(5)：

f(X,U)=

[fL,(X)],fR(X)=；

(5)

其中，

(6)

(7)

引入變量β作為權(quán)系數(shù)，且β∈[0,1], 可把目標(biāo)函數(shù)Minf(X,U)轉(zhuǎn)化為如下單目標(biāo)形式，如式(8)所示：

min(βm(f(X,U))+(1-β)w(f(X,U)))

(8)

3十進(jìn)制離散多目標(biāo)粒子群算法的求解

3.1二進(jìn)制離散粒子群算法

針對實(shí)際工程中存在的組合優(yōu)化問題，Kennedy和 Eberhart[16]結(jié)合二進(jìn)制和粒子群算法提出了離散版二進(jìn)制粒子群算法即BpSO(Binary particle Swarm Optimization)，很好的解決了該問題。在BpSO中對粒子的速度和位置公式進(jìn)行了改進(jìn)，用公式(9)、(10)取代。

v[i][j]=w*v[i][j]+c1*rand()*(l[i][j]-

p[i][j])+c2*rand()*(g-p[i][j])；

(9)

其中，若rand()<1/(1+e-v[i][j])，則p[i][j]=1；否則，p[i][j]=0；

(10)

3.2多目標(biāo)問題模型

多目標(biāo)問題的數(shù)學(xué)形式可以表示為如下模型：

Min y= f(x)=[f1(x)，f2(x)，…fn(x)]

n=1，2，…，N

s.tgi(x)0i=1，2，…m

hj(x)=0j=1，2，…k

X=[x1，x2，…，xD]

針對多個(gè)目標(biāo)在大多數(shù)情況下不能同時(shí)達(dá)到最優(yōu)的問題，通過不斷協(xié)調(diào)各目標(biāo)函數(shù)之間的關(guān)系，直到找出使各目標(biāo)函數(shù)都能盡量達(dá)到最優(yōu)的最優(yōu)解集，通常稱這種解為非支配解或 pareto 最優(yōu)解[17]。

3.3pareto支配

定義1：支配關(guān)系[17-18]：對于?a,b∈Z；若fn(a)≤fn(b)，(n=1,2,…r)；且y∈{1,2,…r}，同時(shí)，有fy(a)< fy(b)，則稱a支配b，表示為 b。其中a>b，稱a是非支配的，b是被支配的，“>”表示支配關(guān)系。

定義2：不相關(guān)關(guān)系：對于?a,b∈Z；若a不支配b且b不支配a，則稱a和b不相關(guān)或者互不支配。

3.4十進(jìn)制離散多目標(biāo)粒子群算法求解過程

設(shè)功能關(guān)聯(lián)的權(quán)重系數(shù)和結(jié)構(gòu)關(guān)聯(lián)的權(quán)重系數(shù)都為0.5，并設(shè)5個(gè)綠色準(zhǔn)則的權(quán)重系數(shù)分別為：0.3564、0.2296、0.2296、0.0922和0.0922[19],β=0.8，定義n個(gè)精英解，n可根據(jù)實(shí)際情況變化。

十進(jìn)制離散多目標(biāo)粒子群優(yōu)化(THDMOpSO)求解步驟如下：

(1)初始化粒子：設(shè)置相關(guān)的參數(shù)、局部最優(yōu)集、定義n個(gè)精英集；將問題的解用十個(gè)隨機(jī)的十進(jìn)制數(shù)表示，產(chǎn)生相應(yīng)粒子群，比如：0,0,1,8,9,5,5,9,9,0；2,2,3,6,6,6,2,5,7,7。數(shù)值相同就表示是同一個(gè)模塊，有多少個(gè)不同的數(shù)值就有多少個(gè)不同的模塊。

(2)更新位置值：在離散二進(jìn)制基礎(chǔ)上改進(jìn)得到離散十進(jìn)制，利用SIGMOID函數(shù)，在每位上按式(11)產(chǎn)生隨機(jī)的離散十進(jìn)制整數(shù)。

particle[i][j]=((int)((1/(1+exp(-v[i][j])))*

RAND_MAX))%10

(11)

(3)更新速度：局部最優(yōu)解依舊選粒子本身的，全局最優(yōu)值由n個(gè)精英解中隨機(jī)產(chǎn)生一個(gè)作為全局最優(yōu)解；按式(12)更新速度。

v[i][j]=w*v[i][j]+c1*1.0*rand()/RAND_MAX*

(loc_best[i][j]-particle[i][j])+c2*1.0*rand()/

RAND_MAX*(glo_best[隨機(jī)][j]-particle[i][j])

；(12)

(4)更新局部最優(yōu)解：計(jì)算多目標(biāo)模型式(1)、(2)、(3),當(dāng)前解與局部最優(yōu)比較，如果非支配就更新，如果是互不支配就按式(13)進(jìn)行均值比較，均值小的保留，fi代表目標(biāo)函數(shù)。

(13)

(5)更新精英解：采用莊家法則，當(dāng)前解分別與精英解集比較，刪除精英解中被支配的解，同時(shí)讓非支配解進(jìn)入精英解集，如果是互不支配的解依據(jù)均值式(13)比較，讓均值大的刪除，騰出空間讓均值小的進(jìn)入精英解集。

(6)按式(13)依靠均值排序輸出均值最小的最優(yōu)解和n個(gè)精英解。

(7)如果達(dá)到迭代次數(shù)或理想結(jié)果就結(jié)束，否則轉(zhuǎn)2步。

3.2實(shí)驗(yàn)數(shù)據(jù)

實(shí)驗(yàn)環(huán)境及參數(shù)設(shè)置：運(yùn)行環(huán)境為C_FREE5.0，編寫程序語言為C語言，粒子數(shù)目100個(gè)，學(xué)習(xí)因子C1=2，學(xué)習(xí)因子C2=3.5，慣性權(quán)重0.5，最大迭代次數(shù)為1000次，目標(biāo)函數(shù)3個(gè)，精英解分別取為n=1，2，3個(gè)來做實(shí)驗(yàn)；獲得的測試數(shù)據(jù)如表4。

表4實(shí)驗(yàn)數(shù)據(jù)

3.3實(shí)驗(yàn)分析

分析實(shí)驗(yàn)數(shù)據(jù)可知，收斂速度非常快，隨著迭代次數(shù)增加，收斂不再變化，模塊劃分不再改變；在只設(shè)置一個(gè)精英解時(shí)候，收斂模塊劃分為：5,0,0,6,6,6,6,9,8,8；在設(shè)置兩個(gè)精英解時(shí)，收斂模塊劃分為6,9,9,0,0,0,0,5,1,1；在設(shè)置三個(gè)精英解時(shí)，收斂模塊劃分為：9,6,6,7,7,7,7,0,3,3；3,7,7,9,9,9,9,6,4,4。結(jié)論表示T1為單獨(dú)模塊，T2、T3為同一模塊，T4、T5、T6和T7為同一模塊，T8為單獨(dú)模塊，T9、T10為同一模塊。實(shí)驗(yàn)所得的結(jié)果剛好符合減速器當(dāng)前成熟的模塊設(shè)計(jì)標(biāo)準(zhǔn)，說明了方法的可行性和合理性。與現(xiàn)有文獻(xiàn)對比，本文研究了綠色模塊劃分過程中含有模糊數(shù)和區(qū)間數(shù)等定性變量的模型，基于二進(jìn)制離散粒子群，提出一種十進(jìn)制離散多目標(biāo)粒子群算法，尤其和文獻(xiàn)[13]比較，本文的研究有幾點(diǎn)特色：①解的求解是引入pareto非支配概念的，在多目標(biāo)求解方法上要優(yōu)于傳統(tǒng)的加權(quán)系數(shù)法；②本文考慮三角模糊變量的同時(shí)，還考慮了區(qū)間數(shù)的定性和確定化方法，更具有實(shí)際生產(chǎn)意義；③本方法非單一解，可能解會(huì)呈多樣性。

4總結(jié)

基于離散二進(jìn)制上改進(jìn)獲得離散十進(jìn)制多目標(biāo)粒子群優(yōu)化方法，對當(dāng)前減速器成熟的模塊劃分進(jìn)行驗(yàn)證，實(shí)例說明了該方法所建立模型及其求解原理的可行性，可以幫助中小企業(yè)進(jìn)行協(xié)同設(shè)計(jì)任務(wù)的模塊劃分，具有非常好的實(shí)用參考價(jià)值。實(shí)驗(yàn)方法收斂速度快，用sigmoid函數(shù)來得到的十進(jìn)制數(shù)，由于sigmoid函數(shù)本身圖形的特性，可能會(huì)引起十進(jìn)制數(shù)取值比較集中在某些數(shù)值，從而出現(xiàn)收斂較早和局部收斂的情況，增強(qiáng)粒子的擾動(dòng)性和突破十進(jìn)制數(shù)取值的局限將是作者下一步的研究方向。

[參考文獻(xiàn)]

[1] 袁群超,賈瑞通,劉兵兵,等.汽車制造業(yè)模塊化可配置BOM研究[J].制造業(yè)自動(dòng)化,2013,35(4):6-9.

[2] 劉飛,曹華軍,何乃軍.綠色制造的研究現(xiàn)狀與發(fā)展趨勢[J].中國機(jī)械工程,2000,11(1-2):105-110.

[3] 王日君,張進(jìn)生,葛培琪,等.模塊化設(shè)計(jì)中模塊劃分方法的研究[J].組合機(jī)床與自動(dòng)化加工技術(shù),2008,12(7):17-21.

[4] 陸長明,陳 峰,鄧勁蓮.綠色性對模塊化產(chǎn)品設(shè)計(jì)的影響[J].機(jī)械設(shè)計(jì)與研究,2006,22(6):13-16.

[5] 李婷婷,龔京忠,李國喜,等.可維修性驅(qū)動(dòng)的模塊劃分[J].機(jī)械設(shè)計(jì)與制造.2007,45(2):166-168.

[6] Tseng H E, Chang C C, Li J D. Modular design to support green life-cycle engineering[J].Expert Systems with Applications, 2008,34(4):2524-2537.

[7] 郭衛(wèi),劉光復(fù),張雷.面向全生命周期的產(chǎn)品綠色模塊劃分方法研究[J].合肥工業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版),2010,33(10):1441-1445,1449.

[8] Smith S, Yen C C. Green product design through product modularization using atomic theory [J].Robotics and Computer Integrated Manufacturing,2010,26(6):790-798.

[9] 陳小斌.機(jī)電產(chǎn)品綠色模塊劃分方法研究與應(yīng)用[D].杭州:浙江大學(xué)機(jī)械工程學(xué)系,2012

[10] Ji Y J, Jiao R J, Chen L, et al. Green modular design for material efficiency: a leader-follower joint optimization model[J],Journal of Cleaner production, 2013, 41(2):187-201.

[11] 唐文獻(xiàn),吳春艷,馬寶,等.基于模糊聚類分析的錨絞機(jī)模塊劃分方法研究[J].機(jī)械設(shè)計(jì), 2012,29(10):24-28.

[12] 徐敬華,張樹有.基于多域互用的數(shù)控機(jī)床模塊化配置設(shè)計(jì)[J].機(jī)械工程學(xué)報(bào),2011,47(17):127-133.

[13] 劉電霆.綠色設(shè)計(jì)中產(chǎn)品模塊劃分的不確定優(yōu)化及GA求解[J].桂林理工大學(xué)學(xué)報(bào),2013,33(4):743-748.

[14] 冉靜學(xué).三角模糊數(shù)排序方法的研究[J].中央民族大學(xué)學(xué)報(bào)(自然科學(xué)版),2011,20(4):37-42.

[15] 王新端.基于區(qū)間數(shù)的不確定優(yōu)化理論及求解方法研究[D].西安:長安大學(xué)應(yīng)用數(shù)學(xué)系,2012:29-32.

[16] 李蘭,改進(jìn)的離散粒子群算法求解0_1背包問題[D].廣州:華南理工大學(xué)理學(xué)院,2011.

[17] Vilfredo pareto. Cours D’Economie politique[M]. volume I and II. F. Rouge, Lansanne,1896.

[18] 賈庭芳,基于粒子群優(yōu)化的離散多目標(biāo)優(yōu)化算法[D].太原:太原科技大學(xué)機(jī)械電子工程,2011.

[19] 唐濤,劉志峰,劉光復(fù),等.綠色模塊設(shè)計(jì)方法研究[J].機(jī)械工程學(xué)報(bào),2003,39(11):149-154.

(編輯李秀敏)

THDMOpSO Green Reducer Module Based on Uncertain Optimization

LIU Dian-tinga,ZHANG Quan-yongb

(a.College of Mechanical and Control Engineering;b.College of Information Science and Engineering, Guilin University of Technology , Guilin Guangxi 541004,China)

Abstract：Aiming at the problems with variable or parameter uncertainty of green product design, a reducer modular green configuration design as an example, as a variable into interval number and fuzzy number, the green design of product module partition problem with uncertain factors, the module division principle and the main steps in the module, internal polymerization between the degree of maximum, minimum and module partition module coupling degree of the green degree is highest for the multiple objective function, a green product module partition of uncertainty optimization model, the interval number and triangle fuzzy number determination, put forward THDMOpSO method, verified the structure of the reducer module structure is reasonable and effective, feasible and the utility value of production.

Key words：uncertain optimization;green design;modular design;decimal discrete multi-objective particle swarm algorithm

中圖分類號(hào)：TH122；TG506

文獻(xiàn)標(biāo)識(shí)碼：A

作者簡介：劉電霆(1966—)，男，江西吉安人，桂林理工大學(xué)教授，博士，研究方向?yàn)闄C(jī)械制造及其自動(dòng)化；通訊作者：張全永(1992—)，男，安徽亳州人，桂林理工大學(xué)碩士研究生，(E-mail)1370006407@qq.com。

*基金項(xiàng)目：國家自然科學(xué)基金項(xiàng)目(51265008)；廣西自然科學(xué)基金項(xiàng)目(2012GXNSFAA053193)；廣西汽車零部件與整車技術(shù)重點(diǎn)實(shí)驗(yàn)室項(xiàng)目(2013KFMS10)；研究生創(chuàng)新項(xiàng)目(YCSZ2014153)；廣西科學(xué)研究與技術(shù)開發(fā)計(jì)劃項(xiàng)目(桂科攻1598007-15)

收稿日期：2015-03-13；修回日期：2015-03-16