MEMS-IMU隨機誤差的Allan方差分析

厲寬寬,陳允芳,程敏,王云鵬

(山東科技大學 測繪科學與工程學院,青島 266590)

MEMS-IMU隨機誤差的Allan方差分析

厲寬寬,陳允芳,程敏,王云鵬

(山東科技大學 測繪科學與工程學院,青島 266590)

隨著微機電系統—慣性測量單元(MEMS-IMU)技術的發展,低成本慣性導航系統(INS)也得到廣泛應用,MEMS-IMU在導航中的應用日益受到重視。但是MEMS-IMU中隨機誤差較大,通常會干擾和覆蓋傳感器中有用的信號,本文采用Allan方差方法對ADIS16405進行實測數據分析,辨別出ADIS16405隨機誤差的種類,并計算確定各誤差項系數。實驗表明該方法可以有效地辨識ADIS16405的主要隨機誤差成分,從而驗證了Allan方差分析法用于MEMS-IMU誤差分析的可行性。

MEMS-IMU;Allan方差;隨機誤差

0 引 言

MEMS-IMU具有體積小、重量輕、成本低、抗沖擊、可靠性高等特點[1-3],在低成本導航系統中得到了越來越廣的應用。但由于MEMS-IMU的精度較低,而導航解的精度又是由IMU輸出值積分得到,因此IMU誤差決定了最終導航解精度。所以如何更好的識別和評價MEMS-IMU誤差的貢獻程度,已成為MEMS-IMU研究的重點之一。根據IMU的誤差特性,慣性傳感器的誤差可以分為確定性誤差和隨機誤差[4]。確定性誤差是傳感器受到某種確切的物理現象的影響而產生的誤差,這些誤差可以在系統運行前,通過轉臺和溫度試驗進行提前標定,并在慣性傳感器內部被修正[4-5]。隨機誤差是由一些不確定因素的干擾而引起的,這類誤差一般通過在線補償來實現。大量研究表明,當確定性誤差被有效的補償后,慣性傳感器的隨機誤差將是影響捷聯慣性導航精度的決定性因素[6]。因此,準確辨識IMU隨機誤差對提高導航精度非常重要。目前,常用的隨機誤差識別方法包括功率譜密度(PSD)、自相關函數估計、Allan方差估計等方法。而絕大多數文獻都采用Allan方差法對MEMS-IMU隨機噪聲特性進行分析。

Allan方差分析法最初是1966年由美國國家標準局的David Allan為了研究原子鐘的振蕩器的穩定性而提出的[2,7],這種方法因其可以克服標準差對包含調頻閃變噪聲時出現的發散而得到廣泛的應用。1980年,Allan方差被引入到陀螺儀的隨機誤差識別中,之后主要在中、低精度激光和光纖陀螺信號性能分析中使用。由于該方法的實用性強1998年Allan方差被IEEE協會選為分析光纖陀螺隨機誤差的推薦方法[8]。在2003年Allan方差第一次被應用到MEMS陀螺儀隨機誤差的分析中,并取得了預期的識別效果[1]。

Allan方差是一種基于時域的分析方法,它的特點是不僅能夠確定產生數據噪聲的基本隨機過程的特性,而且能夠識別給定噪聲項的來源。它能非常容易地對誤差源以及對整個噪聲特性的影響程度進行細致的表征和識別,計算方便,易于分離。

本文主要通過對ADIS16405長時間輸出的實測數據進行Allan方差法分析,并分別對得到的陀螺儀和加速度計的Allan方差-時間雙對數曲線進行分析,結果表明，Allan方差分析法對ADIS16405的隨機誤差進行了有效的識別和分離。

1 Allan方差原理

Allan方差是一種從時域上對信號頻域穩定性進行分析的通用方法,也就是將隨機誤差作為時間序列來處理,描述其均方誤差的方法。下面介紹Allan方差對MEMS-IMU輸出數據的處理過程[6,9-11]:

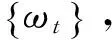
每一組的持續時間τ=Μτ0稱為相關時間。

2) 對于第k個子集,其平均值可以表示為

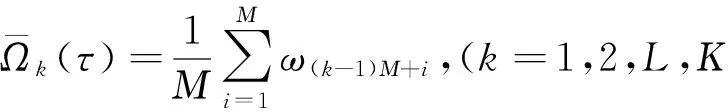
(1)

3) 對每個不同平均時間計算Allan方差:

(2)

式中,〈·〉表示對無限時間序列的總體求平均值。對于不同的相關時間τ,可求得相應的Allan方差,Allan方差的平方根σΑ(τ)通常被稱為Allan均方差。

4) 作出Allan標準差隨平均時間變化的雙對數曲線。然而在實際計算中,無限時間序列的條件是得不到滿足的,隨機誤差的Allan方差可以從Μ個有限采樣點中估計出來。在有限的數據中平均時間增大時,可劃分的獨立子集數目減少,這會導致Allan方差估計質量降低,Allan方差的百分比誤差計算公式為

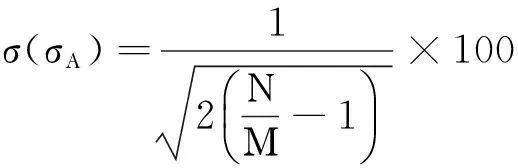
(3)

2 MEMS-IMU隨機誤差分析

MEMS-IMU的實測數據主要含有量化噪聲、角度/速度隨機游走、零偏不穩定性系數、角速率/加速隨機游走、角速率/加速漂移斜坡五種隨機誤差源,以下是對這幾種隨機誤差項的簡要介紹。

1) 量化噪聲(QuantizationNoise)

量化噪聲是一種模擬信號轉換為數字信號而產生的一種誤差,它是由IMU輸出的理想值和量化值之間存在的微小差別而引起的[5]。

2) 角度/速度隨機游走(Angle(Velocity)RandomWalk)

陀螺的角度隨機游走/加速度計的速度隨機游走屬于高頻誤差項,它是由自相關時間小于采樣時間時引起的,然而這種誤差大部分可以通過合理的設計進行消除。

3) 零偏不穩定性噪聲(BiasInstability)

這種誤差的來源是電路噪聲、環境噪聲及其他易受隨機閃爍影響項。由于低頻特性,偏值在數據中表現為波動性。

4) 角速率/加速隨機游走(AnglerRate/AccelerationRandomWalk)

這是一種還沒有確定其來源的隨機過程,可能是有著極長相關時間的指數相關噪聲的極限情況[13]。

5) 角速率/加速漂移斜坡(AnglerRate/AccelerationDriftRamp)

在較長的時間間隔中這種誤差可認為是確定性誤差,而不是隨機噪聲,并持續很長時間。

表1中示出了MEMS-IMU的5種典型隨機誤差項與Allan方差的對應關系。

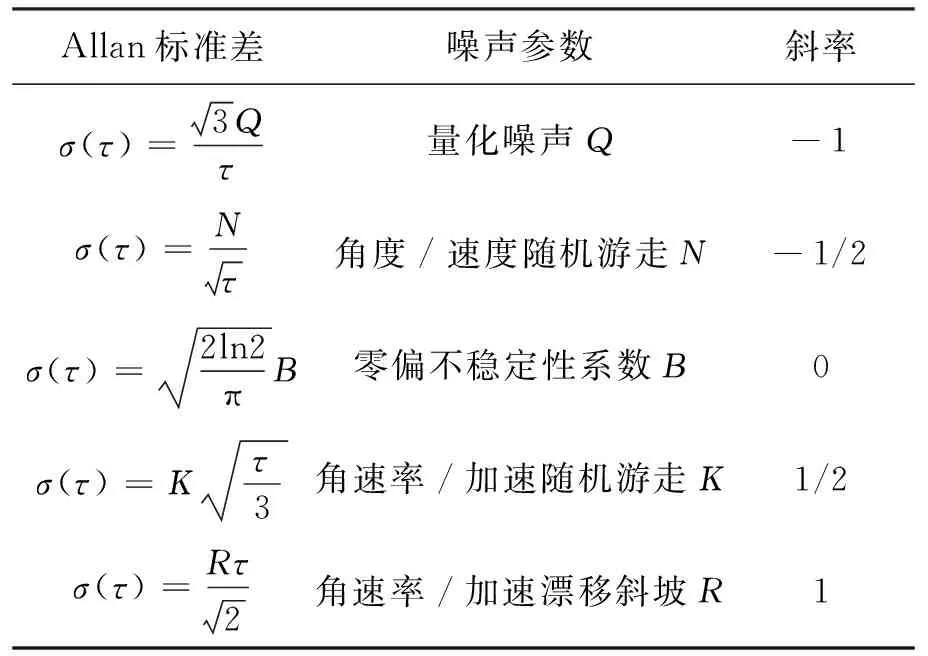
表1 Allan標準差與常見噪聲的對應關系

在利用Allan方差對慣性器件輸出數據進行分析處理時,認為慣性器件輸出數據中的隨機部分是由特定的噪聲源產生的。如果能保證測試環境穩定,可認為各噪聲源相互獨立,則計算出的Allan方差是各類型誤差的平方和[12],即

(4)

整理式(4),得到

(5)

式中,i=(-2,-1,0,1,2).

采用最小二乘法對得到的Allan方差曲線進行擬合,可以得到對應的誤差值及Ci值。再根據對應系數得到相應的誤差系數為

(6)

3 MEMS-IMU實測數據及其誤差項分析

在室溫下對ADI公司生產的ADIS16405慣性傳感器進行數據采集、實驗處理與分析。采用Allan方差法對采集的ADIS16405輸出數據進行處理與分析。圖1為Allan方差流程圖。

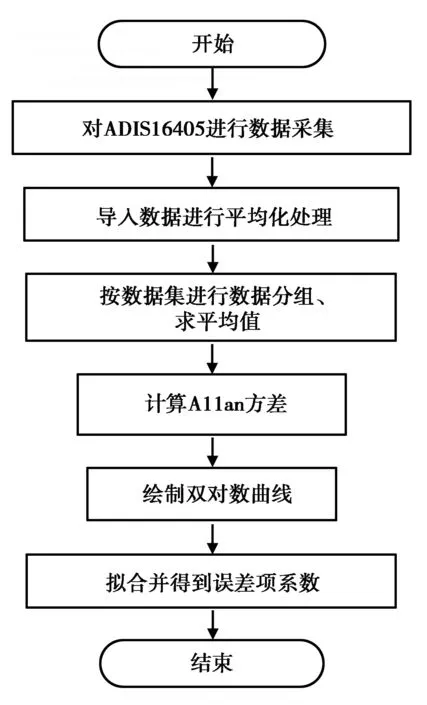
圖1 Allan方差計算流程圖

實驗采集過程中,將慣性傳感器固定在靜止的位置速率轉臺上,由轉臺為其提供水平基準。預熱30min以50Hz的采樣頻率采集4h陀螺儀和加速度計數據,一次采樣得到的ADIS16405陀螺儀和加速度計原始漂移數據如圖2,圖3所示。

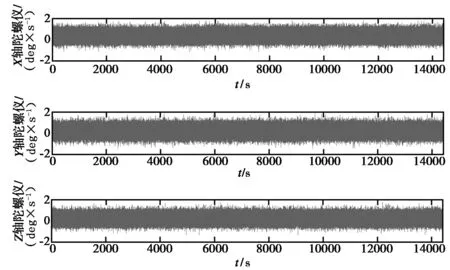
圖2 ADIS16405陀螺儀原始數據

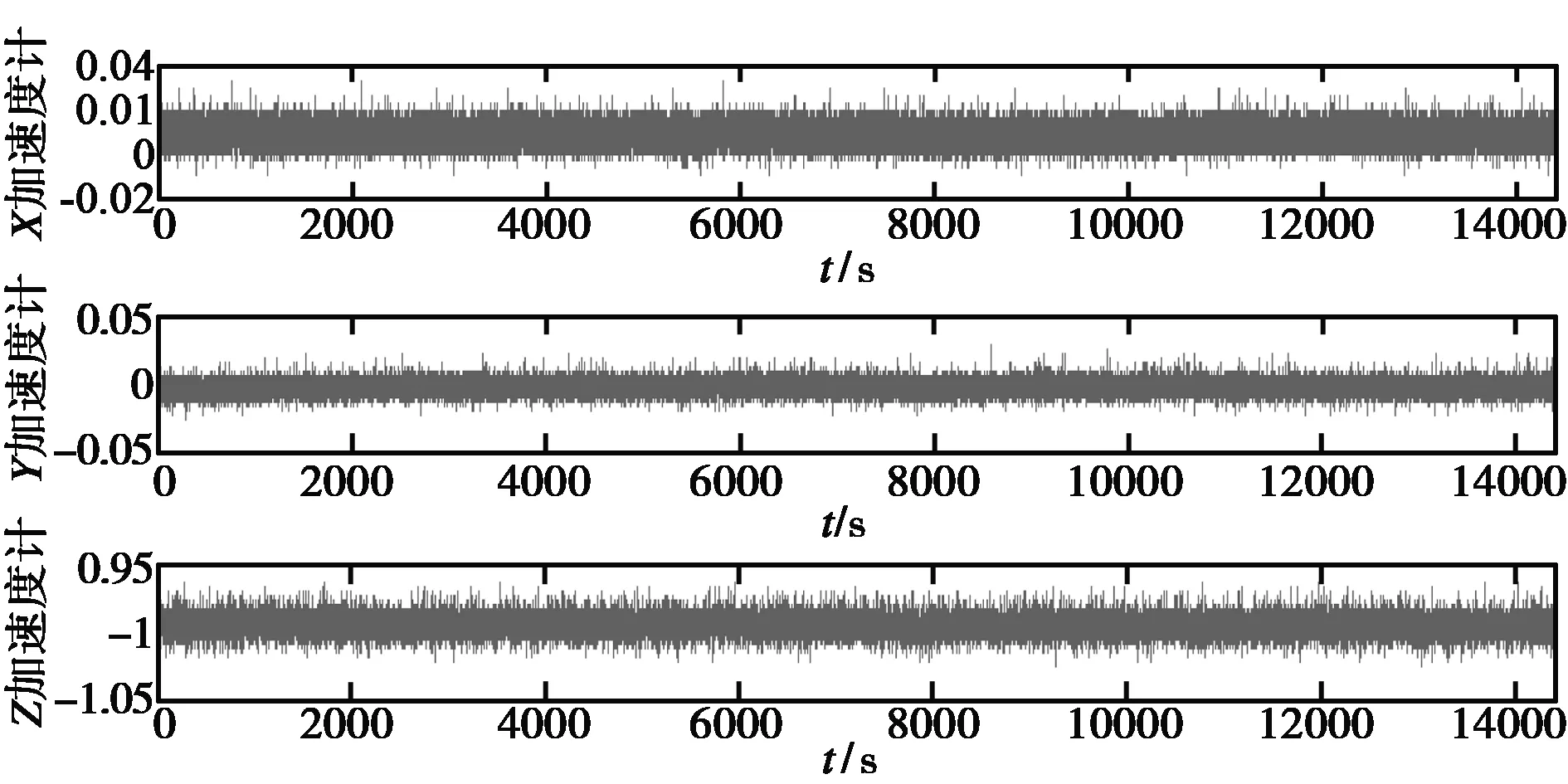
圖3 ADIS16405加速度計原始數據

對采集的數據進行Allan方差分析,得到的結果如圖4和圖5所示,圖4和圖5分別為ADIS16405陀螺儀和加速度計的Allan方差分析結果圖。根據圖中曲線的斜率可知ADIS16405陀螺儀的隨機誤差項主要包含量化噪聲、角度隨機游走和零偏不穩定性,加速度計的隨機誤差項主要包含量化噪聲、速度隨機游走和零偏不穩定性。在平均時間較小的部分,Allan方差曲線的斜率均為-1左右,與其相對應的主要誤差項為量化噪聲Q.圖4中一百到幾千秒量級的平均時間范圍內斜率為-1/2,角度隨機游走Ν是主要誤差項。由圖5中一百到幾百秒量級的平均時間范圍內斜率為-1/2,速度隨機游走Ν是主要誤差項。由圖4、圖5可知,在更大平均時間范圍內斜率為0左右,對應的隨機誤差項為零偏不穩定性Β,對于更長的平均時間而言,限于采集的數據長度用于做Allan方差分析的獨立子集個數有限,因此,其置信程度較低,本文不作分析。

對Allan方差分析結果進行最小二乘擬合可得到各主要誤差項系數(計算結果保留五位有效數字),如表2，表3所示,分別為ADIS16405陀螺儀和加速度計主要誤差項系數。

1) 從表2，表3可知ADIS16405陀螺儀和加速度計的量化噪聲系數都比較小,表明數據采集精度比較高,還可以采用低通濾波器進一步降低量化噪聲以提高ADIS16405 IMU的性能。

2) ADIS16405陀螺儀的角度隨機游走系數較大,說明陀螺儀的電子器件的高頻噪聲比較大,從表3可知速度隨機游走對加速度計也存在較大影響,可以采用頻采樣率和合理設計的濾波來降低該類噪聲的影響,從而提高IMU的性能。

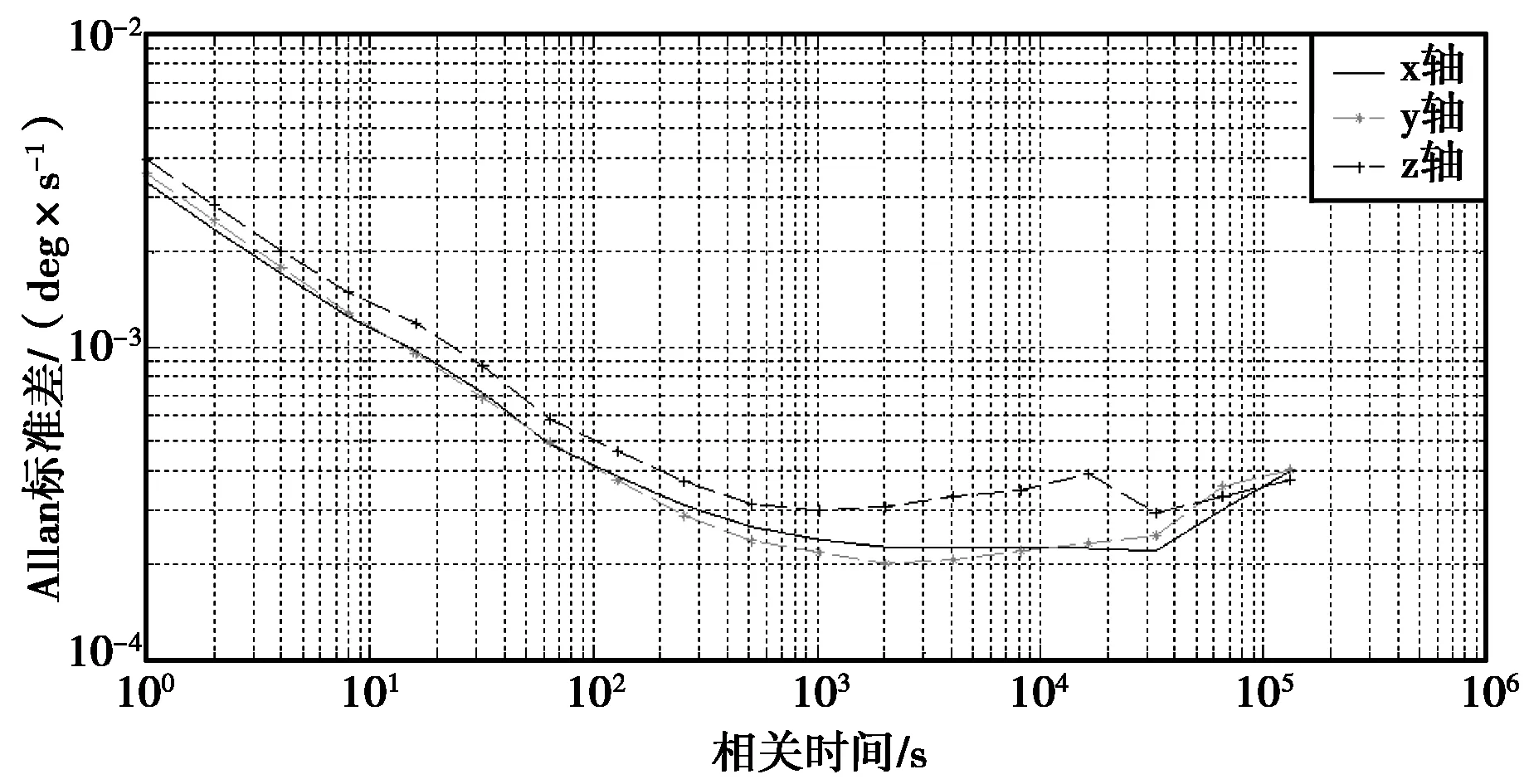
圖5 ADIS16405加速度計Allan方差分析結果圖

3) ADIS16405加速度計的零偏不穩定性系數相對其他項系數較大說明加速度計的電路模塊穩定性較差和環境噪聲影響較大。零偏不穩定性對陀螺儀也有一定的影響。

表2 ADIS16405陀螺儀隨機噪聲系數

表3 ADIS16405加速度計隨機噪聲系數

4 結束語

本文首先給出了Allan方差分析法的基本原理以及各誤差項系數與分析結果之間的對應關系。對ADIS16405的實測數據進行分析,畫出Allan方差-相關時間的雙對數曲線,通過最小二乘擬合得到ADIS16405 IMU的幾種主要隨機誤差系數,說明了Allan方差分析法用于MEMS-IMU誤差分析的可行性。使用Allan方差分析得到的誤差項結果可用于IMU誤差建模、慣導獨立導航以及組合導航等應用方面具有重要指導意義。

[1] WOODMAN O J. An introduction to inertial navigation Tech Rep UCAMCL-TR-696[R]. University of Cambridge, Computer Laboratory, 2007:1-17.

[2] 李榮冰,劉建業,曾慶化,等.基于MEMS技術的微型慣性導航系統的發展現狀[J].中國慣性技術學報,2004,12(6):88-94.

[3] XIA D, YU C, KONG L. The development of micromachined gyroscope structure and circuitry technology[J]. Sensors,2014,14(1):1394-1473.

[4] VACCARO R J, ZAKI A S. Statistical modeling of rate gyros[J]. IEEE Transactions on Instrumentation and Measurement,2012,61(3):673-684.

[5] El-Sheimy N, HOU H, NIU X. Analysis and modeling of inertial sensors using Allan variance[J]. IEEE Transactions on instrumentation and measurement, 2008, 57(1): 140-149.

[6] 嚴恭敏,李四海,秦永元.慣性儀器測試與數據分析[M].北京：國防工業出版社，2012.

[7] ALLAN D W. Statistics of atomic frequency standards[J]. Proceedings of the IEEE, 1966, 54(2): 221-230.

[8] Institute of Electrical and Electronics Engineers. IEEE Standard Specification Format Guide and Test Procedure for Linear, Single-axis, Non-gyroscopic Accelerometers[S]. IEEE Aerospace and Electronic System Society, 2008.

[9] BHARDWAJ R, KUMAR V, KUMAR N. Allan variance the stability analysis algorithm for MEMS based inertial sensors stochastic error[C]//Computing and Communication (IEMCON), 2015 International Conference and Workshop on. IEEE,2015:1-5.

[10]CEMIGLIARO A. Timing experiments with Global Navigation Satellite System clocks[D]. Politecnico di Torino, 2012.

[11]趙思浩,陸明泉,馮振明.MEMS慣性器件誤差系數的Allan方差分析方法[J].中國科學:物理學力學天文學,2010,42(5):672-675.

[12]李京書,許江寧,查峰,等.基于6類噪聲項擬合模型的光纖陀螺噪聲特性分析方法[J].兵工學報,2013,34(7):835-839.

Allan Variance Analysis for the Stochastic Error of MEMS-IMU

LI Kuankuan,CHEN Yunfang, CHENG Min,WANG Yunpeng

(CollegeofGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China)

With the development of MEMS-IMU, low-cost INS has been used widely, as well as the application of MEMS-IMU for INS. However, the large stochastic error will generally interference and override the effective signal in MEMS sensors. In this paper, Allan variance is adopted to analyze the measured data of ADIS16405, identify the types of random errors generated by ADIS16405 and determine the coefficients of individual stochastic error. Experiments demonstrate that this method can effectively recognize the main random errors of ADIS16405, which show the feasibility of Allan variance method applied in the error analysis of MEMS-IMU.

MEMS-IMU; Allan variance; random error

2016-06-29

10.13442/j.gnss.1008-9268.2016.06.020

P228.4

1008-9268(2016)06-0102-05

厲寬寬(1989-),男,河南開封人,碩士生,主要從事慣性導航技術。

陳允芳(1977-),女,博士,碩士生導師，主要從事大地測量學與測量工程專業相關教學和科研工作,研究方向為移動測圖、組合導航與定位及精密工程測量等。

聯系人：歷寬寬 E-mail:13206368478@163.com