基于二維極化特征的PolSAR圖像決策分類

邵璐熠洪 文

①(中國科學院電子學研究所 北京 100190)

②(中國科學院大學 北京 100190)

基于二維極化特征的PolSAR圖像決策分類

邵璐熠*①②洪 文①②

①(中國科學院電子學研究所 北京 100190)

②(中國科學院大學 北京 100190)

決策樹模型在極化SAR數據分類中有著極大的應用價值，既能描述分類結果的極化散射機制，又能獲得較好的分類精度。但在對散射機制相似的地物進行分類時，由于經典決策樹模型的節點采用的是單個特征，分類精度不理想。因此，該文提出了節點采用2維特征的方法，即在特征集相同的前提下，每次取兩個特征組成特征矢量用于節點，提高了經典決策樹難以區分的地物的分類精度；并且利用分類結果的混淆矩陣準確定位了導致分類誤差的節點，進而對節點進行有針對性的反饋調整，進一步提高了指定地物的分類精度。利用AIRSARFlevoland數據驗證了該方法的有效性，并結合極化特征描述了Flevoland地區多種植被的極化散射機制。

決策樹；極化特征；2維特征空間；混淆矩陣；結果反饋調整

1 引言

極化合成孔徑雷達(Polarimetric Synthetic Aperture Radar, PolSAR)具備合成孔徑雷達的全天時全天候工作能力，并且它發射的極化電磁波與觀測目標相互作用后返回，回波中包含了發射與接收極化狀態的各種組合。這些極化組合信息是目標極化散射機制的一種表現形式。極化散射機制包含豐富的內容，能夠反映目標的幾何結構、分布方向、介電特性等；但它本身非常復雜，于是人們運用各種方法從極化組合信息中提取極化特征，試圖描述和解釋目標的極化散射機制。具體到極化SAR數據分類應用時，地物類型不同，極化散射機制也不同，極化特征就會有差異；運用極化特征的差異，可實現不同地物的分類。

根據極化特征的使用方式不同，將極化SAR數據分類的方法劃為兩大類。第1類是直接將極化特征對應地物類別，即運用極化特征描述地物的極化散射機制，同時賦予類別。主要采用模型歸納或者經驗閾值劃分，最早由van Zyl[1]提出，將地物歸納為奇次散射類、偶次散射類、漫散射類及不確定類共4種模型與地物類別。后來，Cloude和Pottier[2]提出了采用矩陣特征值分解的極化特征提取方法，進而將極化特征H,α構成的特征平面用經驗閾值劃分為8個區域，并為每個區域賦予地物類別。由于H-α平面的區域閾值是硬性劃定的，Lee等人[3]采用Wishart統計特性對H-α分類結果進行優化。隨后，Pottier和Lee[4]引入了極化特征A將該方法的類別數增加至16類。相似的思路下，Lee等人[5]發展了基于Freeman-Durden分解的Wishart距離合并算法，將3種極化分解模型及其地物類別與Wishart統計優化相結合。第2類是將極化特征作為機器學習的輸入。在機器學習中，將輸入的、用于分類的測量值稱為特征。對已知類別標記的樣本提取極化特征的數值，輸入分類器中進行學習，得到相應的分類規則，再將規則應用于未分類的樣本即可預測類別，得到分類結果。經典的機器學習方法[6]包括，神經網絡及模糊神經網絡，支持向量機，AdaBoost，隨機森林，馬爾可夫隨機場及條件隨機場等。

第1類方法能夠為地物提供極化散射機制的解釋，利于我們得到關于地物更深刻的物理層面的認識；然而由于類別的賦予受經驗閾值及固定模型的影響，僅在散射機制差異很大的幾類典型地物分類時精度較好。第2類方法在各種地物分類時都獲得了較好的分類精度；但在經典的機器學習方法中，極化特征只是作為數值輸入，失去了物理意義，甚至在得到的分類規則中已經找不到極化特征的痕跡，更無法描述分類結果的極化散射機制。決策樹[7]屬于機器學習的范疇，但它得到的分類規則是嵌入了特征的樹形分級結構，能夠在分類規則中保留輸入特征，簡單、可讀且便于解釋；并且它在賦予類別時，通過學習和歸納已知類別標記的樣本，靈活地采用模型、適應性地調節閾值。因此，采用決策樹分類極化SAR數據，既能描述分類結果的極化散射機制，又能在非典型地物的分類應用中也獲得較好的分類精度[8]。然而，現有決策樹方法在節點上使用的是單個特征，當地物的極化散射機制非常相似時(例如多種植被)，分類精度顯出了不足。

本文分析了決策樹模型和“純度”的概念，介紹了可以用于決策樹的極化特征，并將由2個極化特征組成的2維特征矢量引入決策樹節點，建立了適用于2維特征矢量的決策樹分支準則和分支停止準則，從而解決了節點采用單個極化特征導致相似地物分類精度不足的問題。利用AIRSAR-Flevoland數據實驗，驗證了在特征集相同時，本方法的分類精度優于經典決策樹，提高了相似地物的分類精度；并且利用分類結果的混淆矩陣定位了導致分類誤差的節點，對指定地物的分類精度進行了反饋調整；在對實驗結果的分析過程中，利用極化特征描述了Flevoland地區多種植被的極化散射機制。

2 算法原理

2.1 決策樹模型

決策樹[7]是描述對象屬性與對象值之間映射關系的一種樹形預測模型，具有可讀性，有助于人工分析和解釋；分為名稱型和數字型兩類，數據分類屬于數字型。如圖1所示，ni是節點，表示一種屬性，數字型決策樹的節點必須具備的要素是特征fi和閾值ai，從而繼續分支得到新的節點(或屬性)ni+1;ωi是葉子，表示一個類，不再繼續分支。全部節點特征fi(i=1, 2, ···,m)構成特征集F=｛f1,f2, ···,fm}。

對某個樣本進行決策樹分類時，從根節點n0開始，對樣本的f0特征進行測試，根據測試結果f0＞a0，將樣本分配到其子節點n1，依次遞歸進行測試和分配，直到葉子。而在決策樹的訓練和建樹分支操作中，有一個重要的概念是“純度”，其含義為，若節點所包含的全部樣本均為同種類別標記，則稱該節點是“純”的，決策樹的分支操作也就結束了，節點變為葉子；“純度”的度量方法有很多，例如采用熵、方差、分類錯誤概率等形式[7]。現有的決策樹建樹算法包括ID3、C4.5與CART等[7]，采用的思想是一致的，也就是使分支操作所帶來的“純度”增益最大；而它們的節點采用的都是單個特征。具體來說，分支操作前，節點ni的單個特征fi及其相應閾值ai均未知。此時需要一一考察特征集F中的每一個特征fk(k=1, 2, ···,m)；測量當前節點所包含的全部樣本的fk特征值，遍歷所有相鄰兩數值的中間值，作為fk的候選閾值待定；而單個特征fi及其相應閾值ai的最終確定遵從的是“純度”增益最大原則。fi和ai的確定，標志著節點ni分支操作的完成。對于整棵樹來說，需要設置“純度”增益門限來停止分支，以及采用多數規則來判斷葉子的最終所屬類別。因此，這些算法的分支停止需要依賴門限值，并且會出現過擬合，需要剪枝算法[7]來提升推廣性。

圖1 決策樹模型Fig. 1 The model of decision tree

2.2 用于決策樹的極化特征

所有數值形式的、能夠反映不同地物之間差異的極化特征都可以用于上述決策樹模型。極化SAR數據分類時，對接收到的極化組合信息進行參數化、模型化等處理，可以提取出數值形式的信息，也就是極化特征[9]；通常它們能夠反映同類地物的共性和不同地物之間的差異，因此可以引入決策樹作為節點的特征。在全極化觀測模式下，常用水平(H)-垂直(V)極化收發方式，此時，包含觀測目標影響的散射過程表示為：

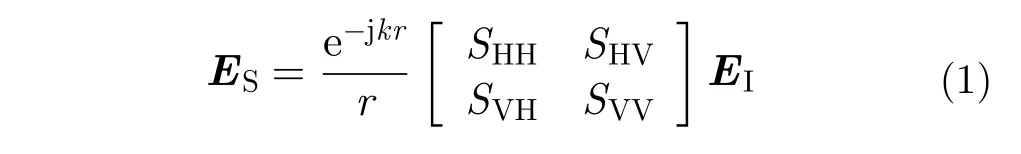
其中，EI和ES分別是入射電磁波和散射電磁波的瓊斯矢量，r是散射體與接收天線之間的距離，k是波數。于是得到了Sinclair極化后向散射矩陣S,SHH和SVV稱為同極化散射系數，SHV和SVH稱為交叉極化散射系數；由于互易性理論，SHV=SVH，散射矩陣簡化為：

對散射矩陣進行圓極化基變換就得到了圓極化分量，即右-右圓極化(RR)、左-左圓極化(LL)以及右-左圓極化(RL)分量，通常變換到其他極化基之后會得到更多樣化的信息。

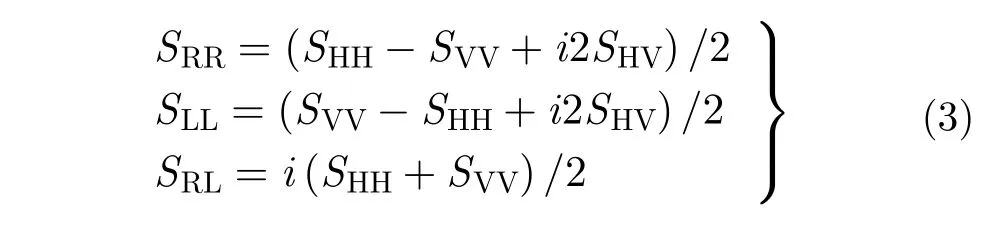
自然地物屬于分布式目標，具有隨機性，常用2階統計量來分析描述。極化協方差矩陣C3與極化相干矩陣T3都是散射矩陣S的2階統計量形式。

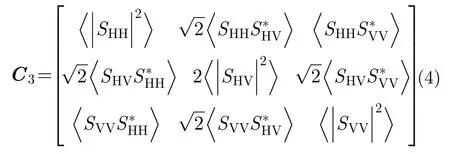
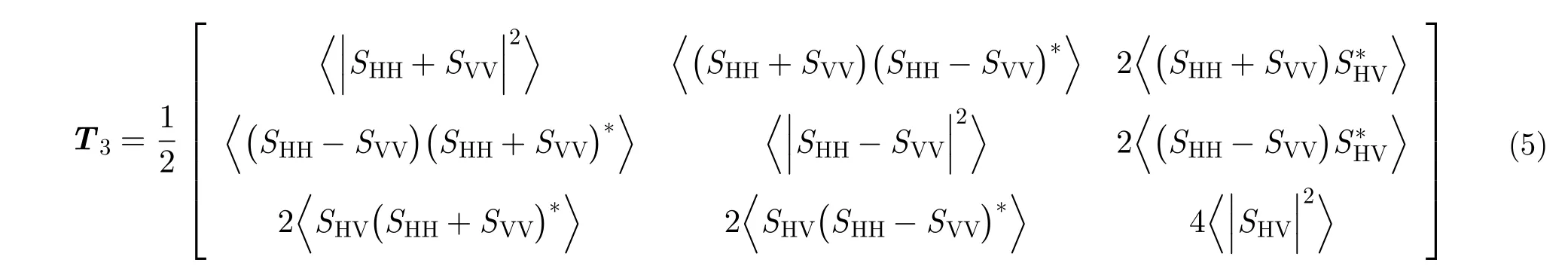
散射總功率SPAN來自2階統計量矩陣C3或T3的對角元素之和，是反映回波功率的信息，與圖像的灰度相聯系，是空間信息的重要表征，可用于圖像的邊緣提取、紋理分析、保留細致結構等。

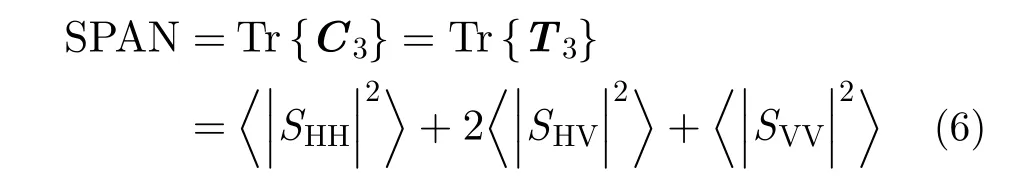
Freeman-Durden(F-D) 3分量分解參數是極化協方差矩陣C3的導出參數，基于3種模型進行極化分解。由于自然地物滿足反射對稱性假設，C3矩陣的同極化項與交叉極化項的相關系數為零；fS代表表面散射模型，fD代表二面角散射模型，fV代表體散射模型，α和β是分解參數，運用數值算法可以確定這5個參數。其中，3種模型參數fS,fD和fV是極化分類中的常用特征。

極化相干矩陣T3的對角元素可以與圓極化比聯系起來。圓極化比CPR定義為右-右圓極化(或左-左圓極化)分量與右-左圓極化分量的比值，即同圓極化與交叉圓極化功率的比值，用來衡量不同通道之間的功率關系，也可以看作是T3對角元素的組合之比。

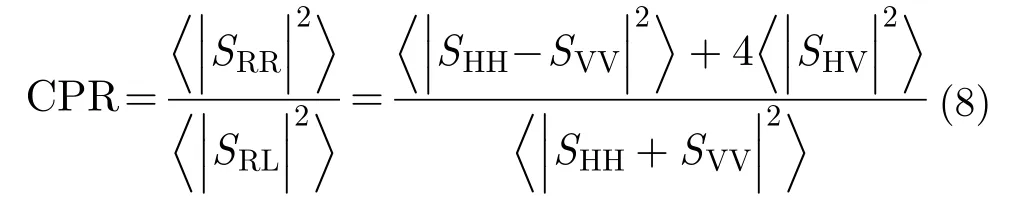
散射角α、極化熵H與極化各向異性度A都是極化相干矩陣T3的導出參數。矩陣T3具有特殊的性質，其共軛轉置矩陣等于自身，在數學上稱為埃爾米特矩陣，這種矩陣進行特征值分解之后所得的特征值為實數。即其中實數λi(i=1, 2, 3)表示T3的特征值；u1,u2和u3分別對應3個正交的單位特征矢量，可以看作是3個互不相關的目標，在散射過程中出現的概率為(k=1, 2, 3)；將特征矢量參數化，聯立求解可以提取出3個正交單位特征矢量的參數α1,α2,α3，結合出現概率得到平均散射角參數：

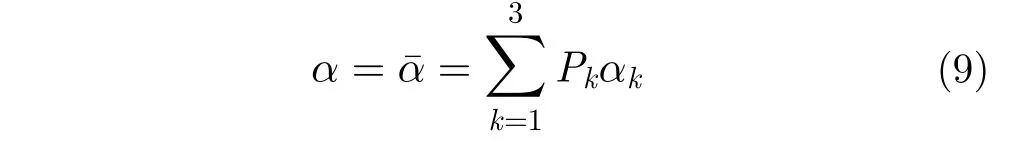
散射角α與平均物理散射機制直接相關，對應于物理散射機制的連續變化，即從表面散射(α=0°)，偶極子散射(α=45°)到二面角散射(α=90°)；由于其旋轉不變性，是極化分類中的常用特征。同樣旋轉不變的還有極化熵H與極化各向異性度A，其中H用來衡量散射過程的隨機性，A用來描述第2個和第3個特征值的相對大小：

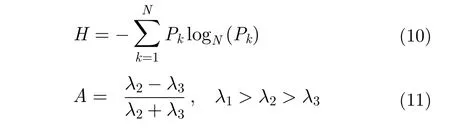
決策樹靈活采用上述模型參數等極化特征作為節點的特征，然后通過調節閾值來分配不同的地物[8]，在分類的同時，也能夠結合極化特征對地物的極化散射機制加以描述。

2.3 2維極化特征與線性可分

分類時可以采用單個特征，也可以采用由l個特征fi(i=1, 2, ···,l)組成的l維特征矢量v=[f1f2···fl]。以特征fi(i=1, 2, ···,l)為坐標軸構建l維特征空間，將樣本描繪在坐標系中，再將這個特征空間分割成不同的類空間，使其中分布的樣本歸屬正確的類，這是對分類的另一種直觀描述[10]。

當采用單個極化特征fi(i=1, 2, ···,l)時，樣本的分布情況是通過直方圖來描述的。選取AIRSARFlevoland數據中的兩類樣本，分別用藍色與紅色表示，圖2(a)統計了它們的散射角f1的取值分布，圖2(b)統計了它們的HH通道后向散射功率f2的取值分布。在直方圖中采用閾值ai(i=1, 2)，可以將樣本劃分為ω1和ω2兩類，即ω1:fi≤ai,ω2:fi＞ai(i=1, 2)。然而，由于兩類樣本的散射機制相似、極化特征值的分布出現混疊，無論怎樣調節閾值都無法避免分類錯誤。

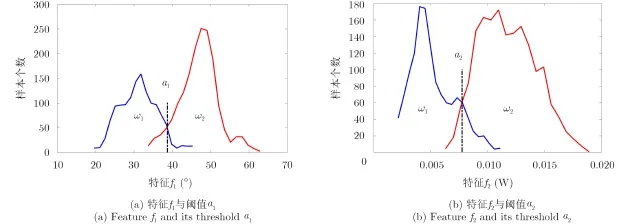
圖2 單個特征與閾值劃分Fig. 2 One single feature and the threshold

當采用由f1和f2組成的2維特征矢量v=[f1f2]時，樣本的分布情況是通過2維平面散點圖來描述的。圖3使用了與圖2相同的數據、樣本以及極化特征(f1和f2)，繪成2維平面散點圖之后，發現原本混疊的兩類樣本完全分離了。這里要用到線性可分[10]的概念，它的定義是，存在某個超平面g(x)=wTv+w0=0，能夠將兩類樣本完全正確地分開；而這個超平面就是2維“閾值”，即邊界。

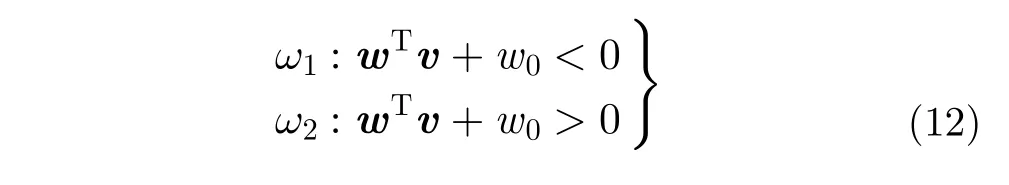
圖3 2維特征矢量與線性可分Fig. 3 The two-dimensional vector of features and linear separable

3 基于2維特征的決策分類方法

由2.3節可知，使用單個極化特征，在劃分散射機制相似的兩類地物時，無論怎樣調節閾值都無法避免分類錯誤；而采用由兩個極化特征組成的2維特征矢量，則可以明顯地提高分類正確率。本節將2維特征與決策樹模型相結合，重點介紹了基于2維特征的決策分類步驟，為此引入Fisher線性判別作為線性可分度量，引入超平面算法作為邊界算法，并采用混淆矩陣計算“純度”，制定了新的分支準則和分支停止準則，最后討論了分類結果的反饋調整。

3.1 線性可分度量與超平面邊界算法

實際應用里的線性可分不是定義中的理想情況，它容許奇異點的存在，不要求所有樣本都完全正確的分類。本文采用Fisher線性判別[11]來度量線性可分，它的原理是借助準則函數值J(w)最大化來確定最佳投影方向，使得投影后的兩類樣本最大程度的分開，

其中，x表示樣本矢量(1維特征)或樣本矩陣(l維特征，l＞1)，由x1和x2兩類樣本構成。w為投影方向，y為樣本的投影，m代表投影樣本的均值，s2代表投影樣本的類內散布即方差。一般來說J(w)值越大，x1與x2兩類樣本的線性可分性越好。因此，J(w)值可以用來度量x1與x2兩類樣本的線性可分性。

若x1與x2線性可分，可以采用超平面算法[12]計算2維“閾值”，即邊界，

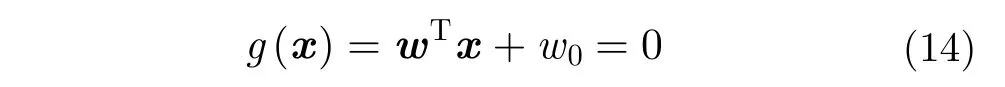
其中，由l維特征矢量展開的特征空間中，w=[w1w2···wl]T是超平面的權向量，w0是常量。

超平面邊界算法不需要概率分布和先驗知識，而是通過數值計算的方法對權向量進行調整來確定最合適的超平面，使得x1與x2獲得較理想的分類正確率。

3.2“純度”度量

x1與x2由超平面劃分邊界之后，統計各個樣本點的類別歸屬與其正確的類別標記是否一致，進而計算混淆矩陣C：

其中，cij表示xi被劃分為xj的樣本數，則第i行元素之和等于第i類的樣本總數。于是，對角元素代表正確分類的樣本數，非對角元素代表錯誤分類的樣本數。為了得到“純度”度量值，對行進行歸一化，使得每一行的元素之和為1：

3.3 分支準則與分支停止準則

決策樹建樹的核心思想是通過對原始樣本集的連續分割，創建與各個類相對應的區域[7]；因此，不斷地分割和更新樣本集是決策樹建樹過程中的一個顯著特點。經典決策樹方法是通過遍歷樣本值來確定閾值從而實現樣本集的分割，然而這種計算單點數值的算法僅適用于單個特征的情況。在2維特征矢量所對應的2維平面散點圖中，區域的分割與樣本聚類的整體分布形狀有關，單個樣本點的計算無意義。因此，本文將樣本子集所形成的聚類作為研究對象，用于分支準則與分支停止準則。

步驟1 選取特征集

選取若干極化特征，構成特征集F=｛f1,f2, ···,fm}，m為極化特征的個數。類別標記已知的k類訓練樣本組成樣本集U=｛u1,u2, ···,uk}；其中，擁有同類標記的樣本子集ui(i=1, 2, 3, ···,k)，稱為類單元。

經典決策樹由單個特征和閾值來完成節點的分支，本文方法則采用2維特征矢量和邊界算法來完成節點的分支。分支過程分為兩個階段，第1階段尋找線性可分的聚類集團，按照線性可分性將樣本集分割成若干子集，每個子集設為一個節點，詳述見步驟2；第2階段對各個節點、亦即線性不可分的各個樣本子集做進一步的細分，直至所包含的類單元唯一，分支停止，詳述見步驟3，兩階段流程見圖4。

圖4 決策樹分支Fig. 4 The branch operation of decision tree

步驟2 決策樹分支的第1階段

將m個極化特征兩兩組合，生成以fi和fj(i=1, 2, ···m;j=1, 2, ···,m;i≠j)為坐標軸的2維平面散點圖Yij，簡稱特征圖。特別地，類單元因為是由同一類樣本組成，在特征圖中往往聚集在一起。若干個類單元ui進一步組成樣本子集Uj，稱為簇；令集合Ij表示簇Uj中所包含類單元的類別標記，

此時，Uj的補集也是一個簇，依據Fisher線性判別計算x1與x2的準則函數值J(w)，認為J(w)值大于Jth的x1與x2線性可分(門限值Jth可調)。對于線性可分的x1與x2，采用超平面算法計算它們的邊界，進而計算劃定邊界之后的混淆矩陣和“純度”。最后，二者里，所包含類單元較少的那個簇，作為候選節點，并將計算所得“純度”賦予該候選節點。從m×(m-1)/2個特征圖中找出所有的候選節點，其中“純度”最大的確定為節點N1。下一步，從樣本集里去掉已選簇中所包含的類單元，更新樣本集，進而生成新的特征圖，用同樣的方法確定節點N2···重復操作，直至生成的新特征圖中不再有線性可分的簇，停止。于是確定了N1,N2, ···,Nh共h個節點，并將最后剩余的線性不可分的簇設置為節點Nh+1。此時，節點Nq對應的樣本子集為Uq(q=1, 2, ···,h,h+1),U1∪U2∪···∪Uh+1=U且兩兩互斥，從而按照線性可分性將樣本集分割成了若干子集。各個節點的分支順序按照下標由小到大依次進行。

步驟3 決策樹分支的第2階段

各個節點是否要繼續分支，判斷準則為樣本子集所包含的類單元的個數。如果類單元個數大于1，繼續分支；如果等于1，分支停止。節點Nq繼續分支之前，假設樣本子集Uq里含有r個類單元，則樣本子集Uq可以表示為：

其中，Iq代表類別標記的集合，共有r個元素。

對每一個類單元uj，將其視作簇則它的補集也是一個簇，采用與第1階段相同的算法來計算之間的邊界和“純度”。選出“純度”最大的類單元uj作為繼續分支的第1個子節點。下一步，去掉該類單元，更新樣本子集，重復上述操作，直至新的樣本子集中只剩一個類單元，分支停止。于是，整棵樹建造完成，可以對未分類的樣本進行預測和分類。將擁有同類標記的樣本子集作為類單元，制定分支和分支停止準則，保證了每個葉子的最終所屬類別在節點分支時就已經確定，不同葉子的最終所屬類別不會出現雷同，避免了過擬合。

3.4 混淆矩陣與反饋調整

兩個分支階段完成，得到了整棵決策樹，用它預測測試樣本的類別，就得到了測試樣本的分類結果。為了評估分類結果，首先，計算總體分類精度，即分類正確的測試樣本數占總測試樣本數的百分比；其次，計算分類結果的混淆矩陣，與“純度”計算中使用的混淆矩陣類似，設總類別數為n，

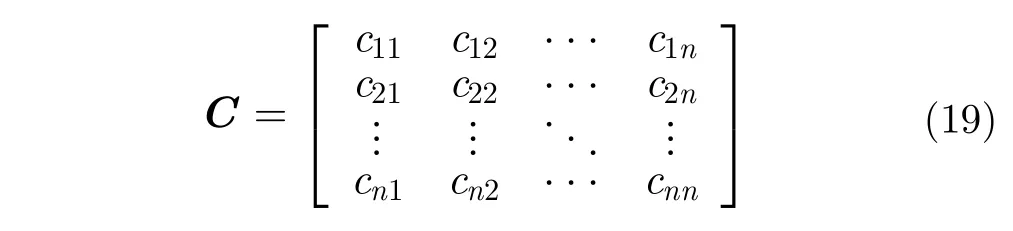
其中，cij表示第i類被劃分成第j類的測試樣本數，于是第i行元素之和等于第i類的測試樣本總數。對角元素代表分類正確的樣本數，非對角元素代表分類錯誤的樣本數。為了分析誤差率，對行做歸一化，使得每一行的元素之和為1。

依據分類結果的混淆矩陣，可以定位每一類地物的錯分樣本來自哪些節點，從而進行反饋調整，進一步提高分類精度。可以采用的反饋調整手段包括：適當調整節點順序，以及修改極化特征等。

4 實驗與結果分析

實驗選用了AIRSAR荷蘭Flevoland地區L波段全極化4視復數據，STK文件格式，含有11類真值(ground-truth)標記數據，分別為莖豆、森林、馬鈴薯、紫花苜蓿、小麥、裸地、甜菜、油菜籽、豌豆、草地和水，其中9類屬于植被，散射機制相似。全圖像素尺寸750×1024，標記樣本所占比例為5.34%。在標記樣本的坐標范圍之內以四邊形框選擇訓練樣本，其余的標記樣本作為測試樣本，具體的樣本數量見表1(a)。另外，為減少相干斑影響，保證極化特征參數的準確性，對數據采用了7×7 Lee濾波的預處理。

表1 樣本集與特征集的選取Tab. 1 The selection of the sample set and feature set(a) 標記樣本與訓練樣本的數量(a) The number of ground-truth samples and training samples

(b) 特征集(b) The feature set

選取8種極化特征參數組成特征集F=｛f1,f2, ···,f8}，詳見表1(b)。選取的參數均為適用于自然地物的2階統計量參數，范圍涵蓋了常用的兩大類，即，直接來自2階統計量矩陣的后向散射系數，以及對2階統計量矩陣進行變換之后導出的極化分解參數。其中，后向散射系數的選取同時考慮了同極化分量、同極化分量之間的相關系數、圓極化基變換下的同極化分量與交叉極化分量的比值，以及各通道分量的總和；極化分解參數的選取主要考慮旋轉不變性，另外加入了描述冠層與植被散射特點的體散射功率參數。

f1是HH后向散射系數為同極化通道HH的后向散射功率。f2是VV后向散射系數為同極化通道VV的后向散射功率。f3是 HH-VV相關項的幅度f4是散射總功率SPAN，見式(6)。f5是F-D分解的體散射功率PV，見式(7),PV=fV，模型來自森林冠層散射。f6是極化散射角α，見式(9)。f7是圓極化比CPR，見式(8)。f8是極化熵與各向異性度組合H(1-A)，見式(10), 式(11)，表征高熵、低各向異性度的隨機散射過程，可描述植被。

4.1 分類結果與分析

決策樹分支的第1階段，需要注意的是，由于裸地和水的回波功率非常接近于零，信噪比太低會導致極化分解參數不準確，有可能干擾各個節點分支的準確性，因此在實際操作中特別規定，回波功率接近于零的地物最先分支。具體做法是，回波功率SPAN分別與另外7個特征依次組合得到7個特征圖，計算每個特征圖中，由裸地和水組成的簇的邊界和“純度”，“純度”最大的簇設為第1個節點A。

接下來按照分支第1階段所述的方法，尋找線性可分的簇(實驗中門限值Jth設為0.005)，依次得到了節點B, C, D和E如表2所示。其中，門限值Jth并沒有統一的設置標準，它的作用是為線性可分的判定提供一個大致的范圍。實際操作時，在特征圖中人工選擇若干個線性可分的簇，分別計算它們的J值，取其中的最小值設置為門限值Jth。一般來說，建議將門限值Jth設置得略低一些，從而盡可能多地保留可分性較好的簇(即候選節點)。

表2 決策樹分支第1階段的線性可分簇Tab. 2 Linear separable clusters in the branch operation for the first phase

決策樹分支的第2階段，對各個節點繼續分支，直至樣本子集中的類單元唯一時，停止分支。

(1) 節點A：裸地+水

由特征矢量[f6f8]繼續分支，將裸地、水分離。

(2) 節點B：紫花苜蓿+草地

由特征矢量[f3f4]繼續分支，將紫花苜蓿、草地分離。

(3) 節點C：莖豆+森林+馬鈴薯

由特征矢量[f5f7]繼續分支，分出莖豆；

由特征矢量[f4f7]繼續分支，將森林、馬鈴薯分離。

(4) 節點D：油菜籽

(5) 節點E：小麥+甜菜+豌豆

由特征矢量[f4f7]繼續分支，分出豌豆；

由特征矢量[f2f4]繼續分支，將小麥、甜菜分離。

利用訓練樣本建樹之后，對測試樣本進行測試，得到了測試結果的混淆矩陣如表3所示；而全體標記樣本的分類結果圖如圖5所示，其他未標記樣本為黑色顯示。

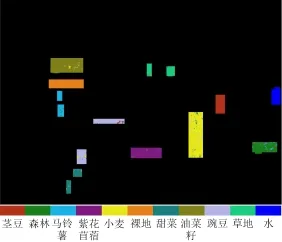
圖5 分類結果圖Fig. 5 The image of classification results

該方法的總體分類精度為95.75%，其中，紫花苜蓿、莖豆、油菜籽、水和裸地5類地物的分類精度都在98%以上，草地的精度也達到了97.47%，馬鈴薯、豌豆、小麥和甜菜4類地物的精度都在92.17%～94.75%之間。需要注意的是，森林的分類精度只有86.81%，且森林和馬鈴薯互相錯分的比例較大(達到8.02%和5.70%)，猜測與森林中的物種構成有關，可能含有灌木或者大小不同的樹種，使其與馬鈴薯在散射特點上出現相似和混淆。

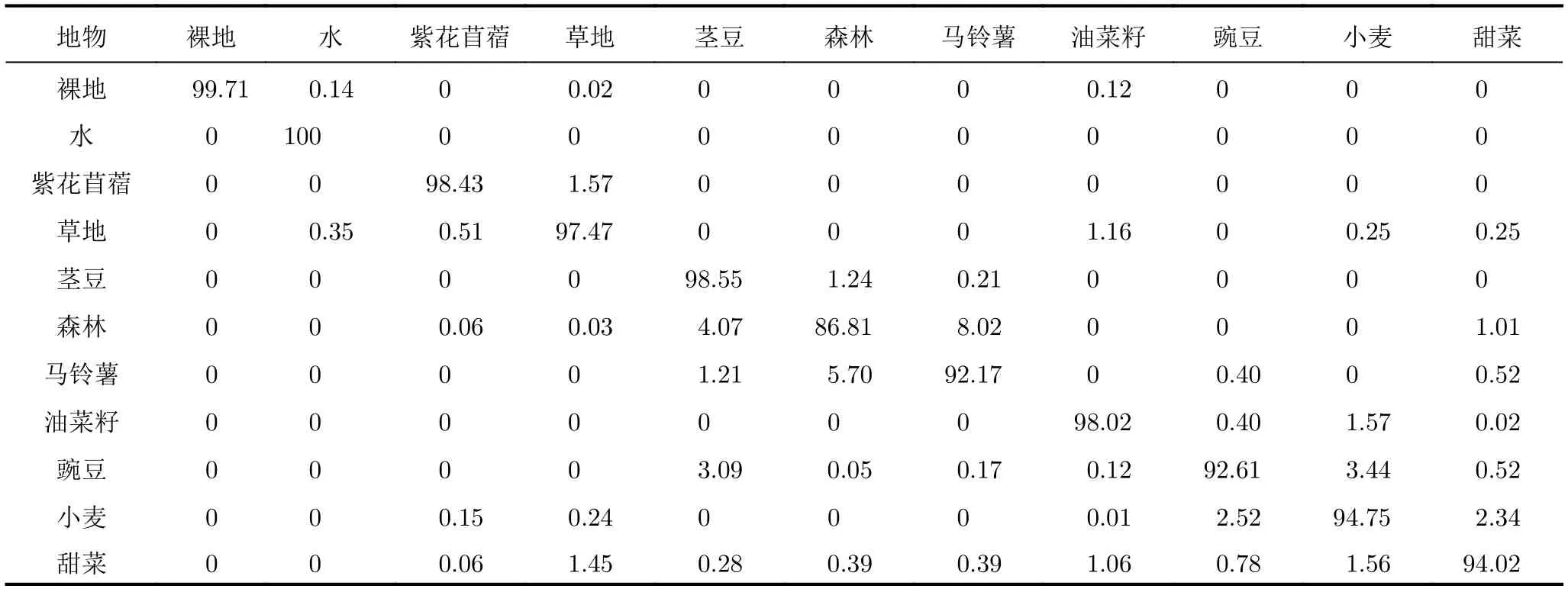
表3 混淆矩陣分類精度(%)Tab. 3 Confusion matrix

另外，表4對比了若干組采用其他分支順序的分類結果的總精度。其中，第1欄代表的是本文采用的分支順序ABCDE，第2欄的分支順序為ACDBE，第3欄的分支順序為ACEBD，第4欄的分支順序為ADCEB，第5欄的分支順序為ABECD。對比發現，本文的總體分類精度優于其他4種順序，說明采用本文的分支準則可以得到最優的分支順序。

在特征集相同時，采用經典決策樹也得到了一組分類結果，與本文分類結果的對比見表5。可以看出，在區分散射機制相似的植被時，本文方法的總體分類精度比經典決策樹提高了6.21%。其中莖豆、馬鈴薯、甜菜的分類精度提高20%～60%；紫花苜蓿、小麥、裸地、草地的分類精度也有1.71%～6.19%的不同程度的提高；油菜籽的分類精度下降0.41%，豌豆的分類精度下降2.18%，總地來說分類精度有了顯著的提高。需要注意的是，經典決策樹對森林的分類精度高達91.98%，但具體分析結果之后發現，91.98%的森林被分為森林的同時，超過60%的馬鈴薯也被錯分為森林，從而導致了馬鈴薯的分類精度只有30.61%；換句話說，森林的高分類精度并不能說明經典決策樹有能力將散射特點相似的森林和馬鈴薯分開，反而是本文的分類結果中，森林和馬鈴薯互相錯分的比例更小、提高了相似地物的分類精度。

表4 不同分支順序的總分類精度對比Tab. 4 Comparation of overall classification accuracy between different sequential decisions

獲得分類結果的同時，也分析了11類地物的極化散射特點：裸地和水以表面散射為主，回波功率小，明顯區別于其他地物；兩者的差異在于，水受風浪影響表面粗糙度更高，散射角較大。森林、馬鈴薯和莖豆三者較為相似，屬于偶極子散射，回波功率大，明顯區別于其他地物；但馬鈴薯和森林都具有森林冠層散射的特點，與莖豆有差異。油菜籽近似于表面散射，而回波功率大，明顯區別于其他地物。紫花苜蓿和草地較為相似，近似于偶極子散射，明顯區別于其他地物；兩者的差異在于，紫花苜蓿更接近森林冠層散射。豌豆、小麥和甜菜三者較為相似，豌豆近似于表面散射，但回波功率較大，可以區別于小麥和甜菜；小麥和甜菜介于表面散射和偶極子散射之間，兩者的回波功率相似，但與極化波的相互作用不同，可以運用同極化通道HH和VV通道的功率差異來區分。綜上，“明顯區別于其他地物”描述的就是決策分支第1階段里的線性可分簇，從相似中尋找“差異”描述的就是決策分支第2階段里的將各個線性不可分的簇進一步細分。先易后難，先粗后細，對目標進行層次分類，是本文方法的主要思想；分析極化特征，描述了Flevoland地區多種植被的極化散射機制的特點，可以為其他植被的散射機制研究提供參考。

表5 本文提出的方法與經典決策樹的分類精度對比(%)Tab. 5 Comparation of classification accuracy between the new method and the traditional decision tree

極化SAR數據分類中常用的隨機性參數H和Freeman-Durden 3種模型的分類體系對植被數據的分類并不理想，這是因為植被的隨機性都比較高，且適用于植被的F-D模型只有體散射模型。本方法的特征集選用了極化散射角和多種回波功率，包括總功率SPAN、散射角α、HH后向散射系數、VV后向散射系數和圓極化比CPR等，實驗證明它們對植被的分類效果良好。

4.2 分類結果的反饋調整

由于樣本的復雜性，各個節點很難達到100%的分類精度，誤差不可避免；而樹狀結構帶來了誤差的累積效應[7]，即：節點的順序越靠后，受前面各節點累積誤差的影響越明顯，甚至有可能超過自身分支的誤差。在植被監測的很多實際應用中，通常只關注一種或者幾種目標地物的情況，對其他無關地物的分類精度則沒有要求。此時，對節點的順序進行適當的調整，雖然降低了總體分類精度(參見表4的分析)，卻可以將目標地物受到的累積誤差的影響盡可能降低。

例如表5提到的，比經典決策樹分類精度下降了2.18%的豌豆，分析表3混淆矩陣可知，豌豆的分類正確率為92.61%，分類錯誤的主要原因之一來自之前的C節點。測試樣本在經由C節點分支后，3.09%的豌豆被錯分成了莖豆，0.05%的豌豆被錯分成了森林，0.17%的豌豆被錯分成了馬鈴薯；也就是總計3.31%的豌豆被錯分到了C節點所包含的樣本子集中。因此，我們嘗試將包含豌豆的E節點調整到C節點之前，即表4中第5欄的分支順序ABECD，得到的分類結果中豌豆的分類精度為94.99%，提高了2.38%，實現了對指定地物分類精度的進一步調整。

如果不存在目標地物與無關地物的概念、所有地物同等重要的情況下，依然可以對分類結果進行改善。仍以豌豆為例，為了減少C節點錯分的豌豆數量，關鍵在于找到更準確區分豌豆與非豌豆的特征。一方面，可以參考2.3節，由單個特征擴展為2維特征矢量時可以將原本有混疊的類分開，于是，可以進一步地由2維擴展為3維甚至更高維的特征矢量；另一方面，可以考慮引入新的極化特征，更新特征集。

綜上，決策樹能夠通過分類結果的混淆矩陣準確定位并找到產生分類誤差的原因，而定位之后，無論節點順序的調整，還是節點特征的分析與修改都成為了可能，從而進一步調整和優化分類結果。另外補充說明一點，分類與反饋調整是兩個相互獨立的階段，當分類精度已經滿足了當前應用需求，或者標記樣本太少的時候，反饋調整的意義不大，可以只完成分類階段。

4.3 問題與展望

決策樹分支的第1階段包含大量循環，計算復雜度明顯高于經典決策樹算法。這一階段的主要目的是尋找線性可分的簇，而為了使用Fisher線性判別分析，必須遍歷若干個類單元的排列組合，這也是導致大量循環的原因。如果能夠找到更加簡單的方法快速定位線性可分的簇，例如引入人機交互參與線性可分簇的篩選等，有望大規模提高運算速度。

4.2 節中提到，節點采用3維或者更高維特征矢量可以進一步改善分類結果，然而，計算的復雜度也變得更高。因此，本文在分類精度與計算復雜度之間作了折中，選取了2維特征矢量作為研究對象，得到了較理想的分類結果(總體分類精度95.8%，與支持向量機SVM的總體分類精度96.6%基本相當)。未來的實驗中，如何更加快速有效地找到線性可分的簇、降低計算復雜度，是3維以及更高維特征矢量得以應用的關鍵。

采用2維或多維特征矢量的決策樹，可以將邊界算法直接融入節點的分支操作中。如3.1節中所述，本文采用了超平面邊界算法，得到的分類結果較為理想。而實際上，采用不同的邊界算法會得到不同的分類精度，進一步提高邊界算法的精度也是未來實驗中可以繼續探討的問題。

5 結束語

基于2維極化特征的決策分類提出了在節點使用2維特征矢量代替單個特征的決策樹分類方法，對Flevoland地區的若干種極化散射機制相似的地物進行分類。得到了更理想分類精度的同時，也獲得了若干種植被的極化散射機制的一些特點，以及極化特征選取的有用結論。從而為類似植被的散射機制研究與分類特征選擇提供了參考。另外，分析分類結果的混淆矩陣，可以定位導致分類誤差的節點；通過節點順序的調整或者節點特征的修改，可以實現對分類結果的反饋調整和進一步優化。

[1]Van Zyl J J. Unsupervised classification of scattering mechanisms using radar polarimetry data[J].IEEE Transactions on Geoscience and Remote Sensing, 1989, 27(1): 36-45.

[2]Cloude S R and Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J].IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78.

[3]Du L J and Lee J S. Polarimetric SAR image classification based on target decomposition theorem and complexWishart distribution[C]. IEEE International Geoscience and Remote Sensing Symposium, Lincoln, 1996, 1: 439-441.

[4]Pottier E and Lee J S. Unsupervised classification scheme of PolSAR images based on the complex Wishart distribution and the H/A/αpolarimetric decomposition theorem[C]. Proceedings of the 3rd European Conference on Synthetic Aperture Radar (EUSAR’00), Munich, 2000: 265-269.

[5]Lee J S, Grunes M R, Pottier E,et al..Unsupervised terrain classification preserving polarimetric scattering characteristics[J].IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 722-731.

[6]Uhlmann S and Kiranyaz S. Integrating color features in polarimetric SAR image classification[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 2197-2216.

[7]Theodoridis S and Koutroumbas K. Pattern Recognition[M]. Fourth Edition, Beijing: China Machine Press, 2009: 215-222.

[8]何楚, 劉明, 許連玉, 等. 利用特征選擇自適應決策樹的層次SAR圖像分類[J]. 武漢大學學報(信息科學版), 2012, 37(1): 46-49. He Chu, Liu Ming, Xu Lian-yu,et al..A hierarchical classification method based on feature selection and adaptive decision tree for SAR image[J].Geomatics and Information Science of Wuhan University, 2012, 37(1): 46-49.

[9]Lee J S and Pottier E. Polarimetric Radar Imaging: From Basics to Applications[M]. Boca Raton, FL, USA, CRC Press, 2009: 55-63, 200-205, 229-245.

[10]李航. 統計學習方法[M]. 北京: 清華大學出版社, 2012: 25-26. Li Hang. Statistical Learning Method[M]. Beijing: Tsinghua University Press, 2012: 25-26.

[11]王明合, 張二華, 唐振民, 等. 基于Fisher線性判別分析的語音信號端點檢測方法[J]. 電子與信息學報, 2015, 37(6): 1343-1349. Wang Ming-he, Zhang Er-hua, Tang Zhen-min,et al..Voice activity detection based on Fisher linear discriminant analysis[J].Journal of Electronics&Information Technology, 2015, 37(6): 1343-1349.

[12]滑文強, 王爽, 侯彪. 基于半監督學習的SVM-Wishart極化SAR圖像分類方法[J]. 雷達學報, 2015, 4(1): 93-98. Hua Wen-qiang, Wang Shuang, and Hou Biao. Semisupervised learning for classification of polarimetric SAR images based on SVM-Wishart[J].Journal of Radars, 2015, 4(1): 93-98.

邵璐熠(1987-)，女，中國科學院電子學研究所在讀博士生，研究方向為極化SAR分類及應用。

E-mail: shaoluyi28@126.com

洪 文(1968-)，女，中國科學院電子學研究所研究員，博士生導師，研究方向為雷達信號處理理論、SAR成像算法、微波遙感圖像處理及其應用等。

E-mail: whong@mail.ie.ac.cn

Decision Tree Classification of PolSAR Image Based on Two-dimensional Polarimetric Features

Shao Luyi①②Hong Wen①②

①(Institute of Electronics,Chinese Academy of Sciences,Beijing100190,China)

②(University of Chinese Academy of Sciences,Beijing100190,China)

The decision tree model has great significance in the application of polarimetric SAR data classification, whose results in many types of classification applications obtain good accuracy and are interpretable by polarimetric scattering mechanisms. In the traditional decision tree model, because one single feature is employed by the nodes of the decision tree, the accuracy of the classification result tends to be poor, especially, for applications that classify objects with similar scattering characteristics. In this paper, we propose an improved method to create a two-dimensional vector of features instead of one single feature at the decision nodes. As a result, the classification results of the new method adopting the same feature set as the traditional decision tree can achieve better accuracy. In addition, after classification, the new method may employ a confusion matrix to identify the decision node that yields a classification error, which will facilitate the objectoriented feedback adjustment of classification results, thus making it possible to improve the classification accuracy of the specified object. Our experimental results with AIRSAR-Flevoland data prove the validity of the proposed method, and we draw some useful conclusions about the scattering characteristics of several types of vegetation.

Decision tree; Polarimetric features; Mapping of two-dimensional feature; Confusion matrix; Adjustment of the classification results

TP753

A

2095-283X(2016)06-0681-11

10.12000/JR16002

邵璐熠, 洪文. 基于二維極化特征的PolSAR圖像決策分類[J]. 雷達學報, 2016, 5(6): 681-691.

10.12000/JR16002.

Reference format:Shao Luyi and Hong Wen. Decision tree classification of PolSAR image based on twodimensional polarimetric features[J].Journal of Radars, 2016, 5(6): 681-691. DOI: 10.12000/JR16002.

2016-01-05；改回日期：2016-06-20；

2016-07-22

*通信作者：邵璐熠 shaoluyi28@126.com

國家自然科學基金(61431018)

Foundation Item: The National Natural Science Foundation of China (61431018)