高考對于導數研究函數的單調性的考察

王衛東

內蒙古呼和浩特市第十四中學

高考對于導數研究函數的單調性的考察

王衛東

內蒙古呼和浩特市第十四中學

函數是高中數學教學的主干線，同時歷年高考的重要考點。縱覽最近今年高考試卷中的高考數學試卷，不難發現函數的單調性是近幾年高考中的熱點和難點，而導數是解決函數的單調性問題的有力工具。

一、導數判斷函數的單調性

解決此問題的依據是：設函數f（x）在某個區間（a，b）內的導數為f’（x），那么當f’（x）取不同的值時，所對應的函數的單調性也不相同。

（1）若f’（x）＞0，則函數f（x）在區間（a，b）內是遞增的；

（2）若f’（x）＜0，則函數f（x）在區間（a，b）內是遞增的；

（3）若f’（x）=0，則函數f（x）在區間（a，b）內是遞增的。

二、解決的問題

縱觀2016年高考數學試題，其中利用函數的導數來解決函數的問題主要包括以下幾類。

（1）利用導數研究函數單調性，求解函數的單調區間；

（2）通過函數在某區間上的單調性來求解參數的取值范圍。

而第2類問題又是是建立在第一類問題的基礎之上。

下面結合2016年高考中出現的與通過導數來解決函數單調性的試題，進行分析。

三、真題解析

例1（2016北京理科，18）。

設函數f(x)=xea-x+bx，曲線y=f(x)在點(2,f(2))處的切線方程為y=(e-1)x+4，

（1）求a，b的值；

（2）求f(x)的單調區間。

[答案]（Ⅰ）a=2，b=e；（2）f(x)的單調遞增區間為(-∞,+∞)。

[解析]

（1）因為

（2）f(x)=xea-x+bx，所以f’(x)=(1-x)ea-x+b。

解得a=2，b=e；

（2）由（1）知f(x)=xe2-x+ex

由f’(x)=(1-x+ex-1)e2-x，即e2-x＞0，所以f’(x)與(1-x+ex-1)同號。

令g(x)=1-x+ex-1，則g’(x)=-1+ex-1

所以，x∈(-∞,1)時，g'(x)＜0，g(x)在區間上單調遞增。

所以g（1）=1是g（x）在區間(-∞,+∞)上的最小值，

所以g(x)＞0,x∈(-∞,+∞)，

綜上所述，f'(x)＞0,x∈(-∞,+∞)，所以（fx）的單調遞增區間為(-∞,+∞)。

[試題分析]這道題考察的是利用導數來求解函數的單調區間，首先要求出的導數值（1）根據題意求出f'(x)，根據f(2)=2e+2，f'(2)=e-1，求a，b的值；（2）由題意知判斷f'(x)，即判斷g(x)=1-x+ex-1的單調性，知g(x)＞0，即f'(x)＞0，由此求得f(x)的單調區間。

例2（2016全國卷，21（I））

[解析]

f(x)的定義域為(-∞,-2)∪(-2,+∞).

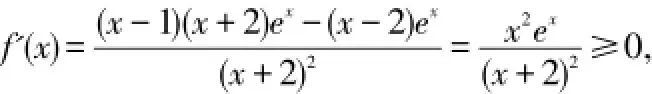
且僅當x=0時，f'(x)=0，所以f(x)在(-∞,-2),(-2,+∞)單調遞增，

因此當x∈(0,+∞)時，f(x)＞f(0)=-1,

所以(x-2)ex＞-(x+2),(x-2)ex+x+2＞0。

[試題分析]這道題考察的是利用導數來判斷函數的單調性，并確定函數的極值與最值。解答這道題，先求定義域，用導數法求函數的單調性，當x∈(0,+∞)時，f(x)＞f(0)證明結論。

四、總結

最開始導數知識是本科教育高等數學中的模塊，教育改革中將導數知識下放到高中教學中。但是高中對于導數的研究，并不會像大學那樣的系統和深刻。考生在處理導數問題時，首先要先掌握導數概念自身的抽象性，很多學生對導數基礎知識理解不透徹都有可能解答不出相應的試題。這就導致學生會出現認知盲點的問題，出現失誤。教學過程中，教師應結合新課標對導數的要求，采取積極的教學策略策略；引導學生去正視錯誤，分析錯誤，改正錯誤，再多加練習，進而加深對相關概念的理解。