考慮剪切效應時雙模量梁的自由振動

吳　曉, 黃志剛, 楊立軍

(湖南文理學院，湖南　常德　415000)

?

考慮剪切效應時雙模量梁的自由振動

吳曉, 黃志剛, 楊立軍

(湖南文理學院，湖南常德415000)

在土木、機械等實際工程中，振動問題是較為常見的力學現象。在結構的振動過程中，結構的形狀、承載力會在極短的時間內發生急劇的變化，對結構的工作性能和使用壽命會產生嚴重的影響。因此，工程設計人員對結構的振動問題一直極為關注。大量的試驗和研究表明，材料在絕對值相同的拉應力或壓應力作用下，會發生絕對值不同的拉應變或壓應變，即材料具有明顯的拉壓彈性模量不同的雙模量性質。事實上，許多工程材料都在不同程度上表現出雙模量特性，如混凝土、復合材料等材料。工程設計中對材料的雙模量特性一般不予區分，現仍沿用經典彈性理論分析計算雙模量結構，在某些情況下會因本構關系不符合造成較大誤差，有可能成為工程結構失效的隱患。所以，在梁、彈性平面等問題的結構中，已經開始考慮材料的雙模量特性。文獻[1-2]采用有限元法分析了雙模量材料板的變形，文獻[3-5]研究了雙模量材料的本構關系及簡單的彈性平面問題，文獻[6-7]研究了雙模量材料的簡單桁架問題，文獻[8]研究了雙模量圓板中心在沖擊載荷作用下的彈性計算，文獻[9-13]研究了雙彈性模量材料板的彎曲問題，文獻[14]研究了不同模量彎壓柱的解析解并證明了軸向力對雙模量梁中性軸位置有影響，文獻[15]研究了拉壓不同模量橫力彎曲梁的解析解，文獻[16]研究了不同模量彎曲梁的自由振動。本文利用雙模量材料純剪切應力狀態單元體，推導出了雙模量材料剪切彈性模量表達式，在考慮剪切效應的基礎上，研究了雙模量梁自由振動問題。

1雙模量材料剪切彈性模量

在實際工程中，由于結構受力多以平面應力狀態居多，所以本文僅以雙模量材料結構的平面應力狀態為例，討論其應力與應變關系。當雙模量材料結構處于平面應力狀態，其受力單元體如圖1所示。

對于圖1所示雙模量材料平面應力狀態單元體，可知其應力與應變關系分別為

(1a)

(1b)

(1c)

(1d)

式中：E1、μ1為拉伸彈性模量、泊松比，E2、μ2為壓縮彈性模量、泊松比。

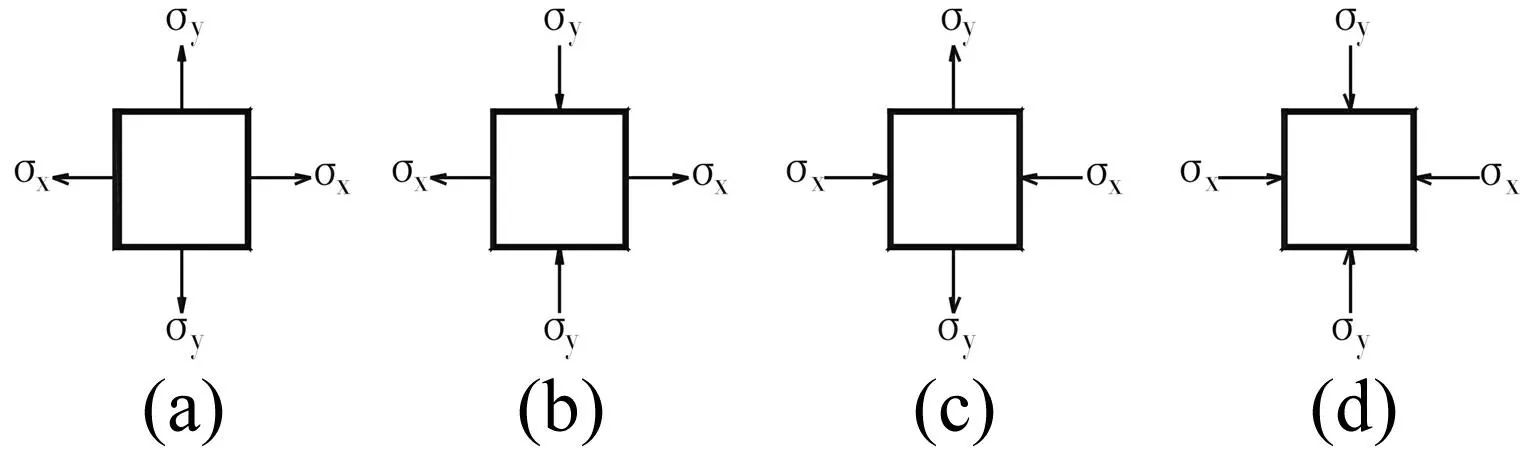
圖1　雙模量材料單元體Fig.1 Unit body of bimodulous material

圖2(a)所示雙模量材料圓軸扭轉時，可知其受力單元體為圖2(b)所示純剪切狀態，所以由材料力學理論可以得到

(2)

式中：d為圓軸直徑。

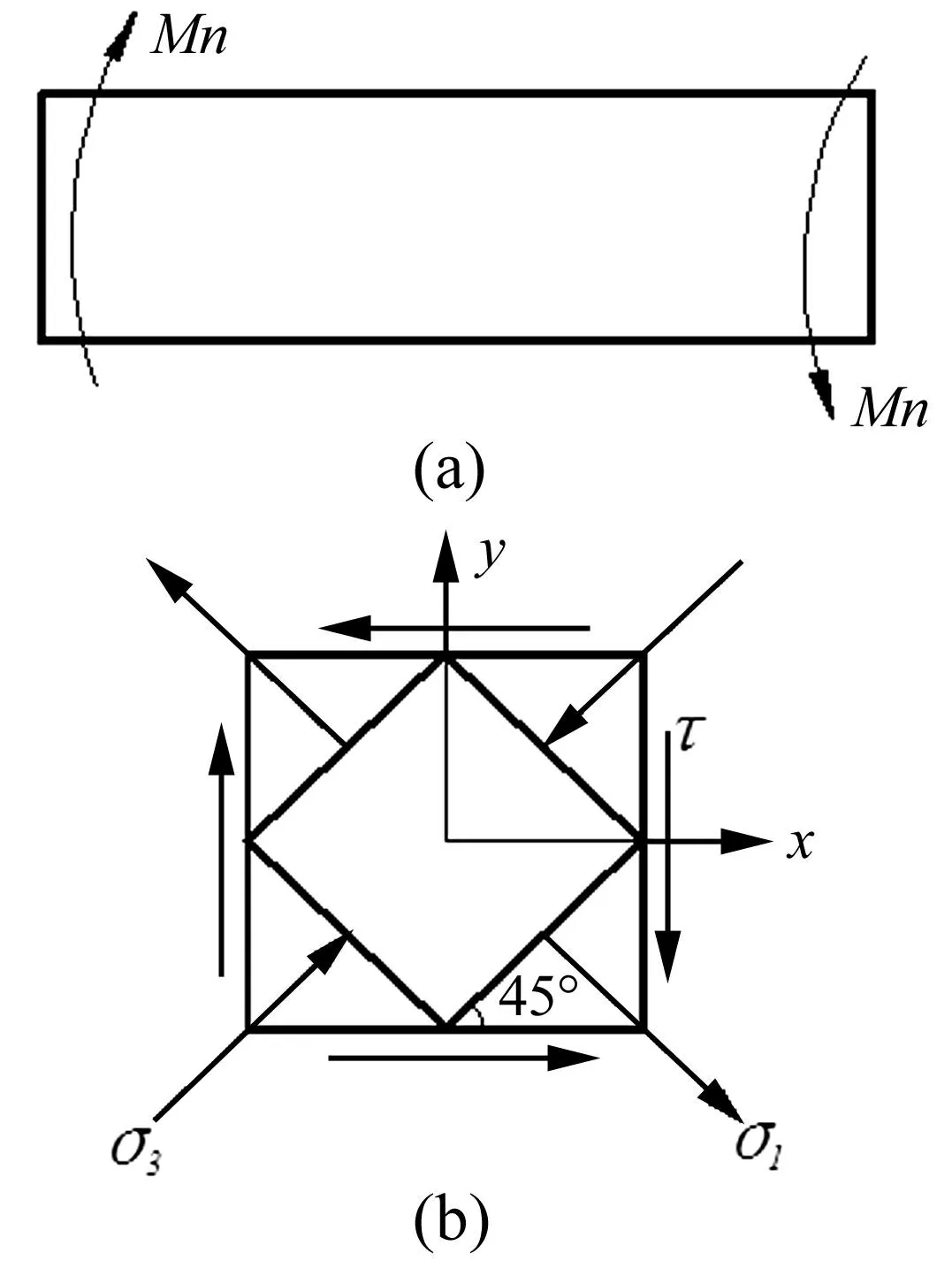
圖2　雙模量扭轉模型Fig.2 Bimodulous torsion model

利用式(1b)或式(1c)及式(2)可以求得

(3)

由材料力學應變公式可得以下各式

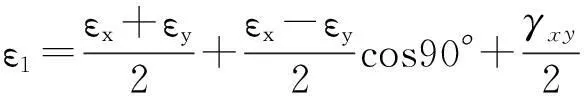
(4a)

(4b)

利用式(3)、式(4)可以求得

(5)

由于γxy=τ/G，雙模量材料剪切彈性模量為

(6)

2確定中性軸位置

因為雙模量連續梁在外載荷作用下會形成拉壓彈性模量不同的拉伸區和壓縮區，所以研究雙模量梁的變形還需要確定其在外載荷作用下的中性層位置。由彈性理論可知雙模量梁彎曲時其拉壓區應力和應變關系為

(7)

假設圖3所示雙模量梁在任意載荷作用下發生彎曲變形，且使梁產生的彎矩全都是正彎矩或全都是負彎矩時，以A點為力矩支點可知

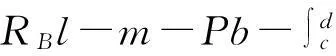
(8)

圖3　載荷作用下雙模量梁Fig.3 Bimodulous beam under loads

由式(8)可以求得簡支梁的支反力為

(9a)

(9b)

雙模量梁的支座約束反力確定后，即可寫出雙模量梁任意截面的彎矩表達式M(x)。

雙模量梁彎曲時其橫截面內力應滿足以下關系

(10a)

(10b)

可把式(7)代入式(10)中得到下式

(11)

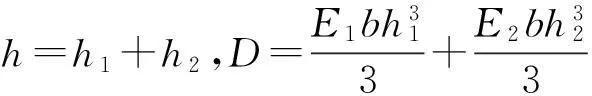
文獻[14]已經證明了軸向壓力對雙模量梁中性軸的位置有較大影響。以上推導的雙模量梁中性軸位置公式與文獻[15]的結果一致，由此可知作用在雙模量梁上的橫向載荷，對任意邊界條件下的雙模量梁中性軸位置無影響。

3振動微分方程

假設雙模量梁坐標方向如圖3所示。橫坐標軸與梁振動時的每個周期的前半波梁段，在初始狀態即未振時的中性軸重合。由材料力學理論可知雙模量梁的彎矩及剪力表達式分別為

(12)

由材料力學理論可知梁微段平衡方程為

(13a)

(13b)

利用式(12)、式(13)可以得到雙模量梁的振動微分方程為

(14)

假設雙模量梁無外載荷作用即q=0，可令橫振位移的表達式為

y(x,t)=Y(x)sin(ωt+φ)

(15)

把式(15)代入式(16)中可得

(16)

由式(16)可以求得雙模量梁自由振動振形函數為

Y(x)=A0sinαx+B0cosαx+C0shβx+D0chβx

(17)

式中：A0、B0、C0、D0均為常數。

對于簡支雙模量梁的自由振動，可知其邊界條件為

(18)

把式(17)代入式(18)中可以得到簡支雙模量梁自由振動時沿x軸方向的振型函數為

(19)

簡支雙模量梁的固有頻率表達式為

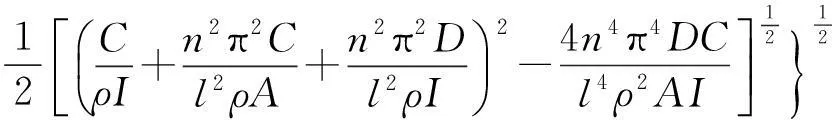
(20)

對于簡支雙模量梁固有振動，由于每個周期的前半波梁段的中性軸與x軸方向重合，所以振型函數為式(19)。而每個周期的前半波梁段中性軸的波型與后半波梁段的波型相反，由此導致每個周期的前半波梁段的拉伸區、壓縮區與后半波梁段的拉伸區、壓縮區也相反，前半波梁段中性軸與后半波梁段中性軸之間的距離相差(h1-h2)，所以后半波梁段中性軸的波型函數為

(n=2,4,…)

(21)

所以，簡支雙模量梁自由振動時，n為奇數時的梁段中性軸的波型表達式為式(19)，n為偶數時的梁段中性軸的波型表達式為式(21)。

對于邊界條件為其它支承雙模量梁的自由振動，利用其邊界條件及式(17)，采用上述方法同樣可以確定雙模量梁自由振動的振型函數及固有頻率。

4算例分析

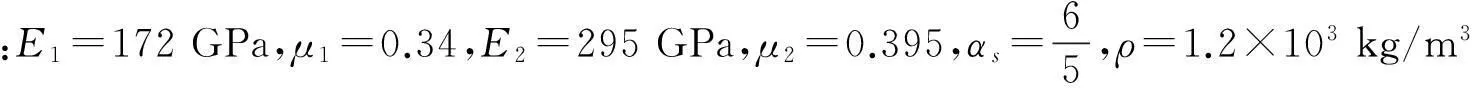
下面把不考慮剪切效應對雙模量梁自由振動影響時的頻率，與考慮剪切效應對雙模量梁自由振動影響時的頻率均列在表1中。

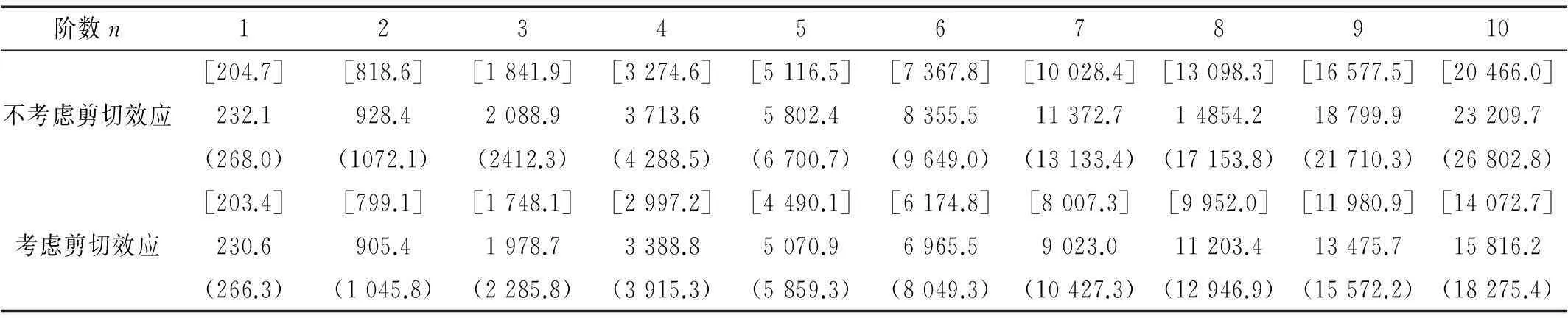
表1　簡支雙模量梁固有頻率w (rad/s)

注：在表1中，括號[]中數據為E1=E2=172 GPa、m1=m2=0.34時簡支單模量梁固有頻率，括號()中數據為E1=E2=295 GPa、m1=m2=0.395時簡支單模量梁固有頻率，無括號數據為簡支雙模量梁固有頻率。

對表1進行分析可以看出：雙模量梁固有振動頻率與單模量梁固有振動頻率的誤差均在12%或16%以上，超過了工程允許的誤差，這說明拉壓彈性模量相差較大時，雙模量梁固有振動不宜采用單彈性模量經典彈性理論，而應采用雙彈性模量彈性理論，否則會引起較大的誤差。不考慮剪切效應對雙模量梁固有振動影響時的頻率與考慮剪切效應對雙模量梁固有振動影響時的頻率，當簡支雙模量梁固有振型為1、2階數時，兩者誤差分別為1.0%、3.0%，均在工程允許誤差的范圍內; 當簡支雙模量梁固有振型為3階數以上時，兩者誤差分別為6.0%超過了工程允許的誤差。并且隨著簡支雙模量梁固有振型階數升高，兩者誤差越來越大，當簡支雙模量梁固有振型為10階數時兩者誤差達47%。這說明剪切效應對雙模量梁固有振動低階振型時的頻率影響不大，對高階振型時的頻率是隨著振型階數升高影響越來越大。所以，對雙模量梁固有振動高階振型時的頻率計算，必須要考慮剪切效應的影響

5結論

(1) 拉壓彈性模量相差較大時，雙模量梁固有振動不宜采用單彈性模量經典彈性理論，而應采用雙彈性模量彈性理論，否則會引起較大的誤差。

(2) 剪切效應對雙模量梁固有振動低階振型時的頻率影響不大，對高階振型時的頻率是隨著振型階數升高影響越來越大。雙模量梁固有振動高階振型時的頻率計算，必須要考慮剪切效應的影響。

(3) 雙模量梁自由振動時，奇數波型與波型振型是不連續的存在間斷點。

參 考 文 獻

[1] Medri G. A nonlinear elastic model for isotropic materials with different behavior in tension and compression [J]. Transactions of the ASME, 1982, 26(104): 26-28.

[2] Srinivasan R S, Ramachandra L S. Axisymmetric nonlinear dynamic response of bimodulous annular plates [J]. Journal of Vibration and Acoustics, 1990, 112(2): 202-205.

[3] 阿巴爾楚米揚. 鄔瑞鋒, 張允真譯. 不同模量彈性理論[M]. 北京: 中國鐵道出版社, 1986: 274-275.

[4] 蔡來生, 俞煥然. 拉壓模量不同彈性物質的本構[J]. 西安科技大學學報, 2009, 29(1): 17-21.

CAI Lai-sheng, YU Huan-ran. Constitutive relation of elastic materials with different elastic moduli in tension and compression [J]. Journal of Xi’an University of Science and Technology, 2009, 29(1): 17-21.

[5] 羅戰友, 夏建中, 龔曉南. 不同拉壓模量及軟化特性材料的柱形孔擴張問題的統一解[J]. 工程力學, 2008, 25(9): 79-84.

LUO Zhan-you, XIA Jian-zhong, GONG Xiao-nan. Unified solution for expansion of cylindrical cavity in strain-softening materials with different elastic moduli in tension and compression [J]. Engineering Mechanics, 2008, 25(9): 79-84.

[6] 張曉月. 基于敏度分析的不同模量桁架正反問題求解[D]. 大連: 大連理工大學, 2008.

[7] 楊海天, 張曉月, 何宜謙. 基于敏度分析的拉壓不同模量桁架問題的數值分析[J]. 計算力學學報, 2011, 28(2): 237-242.

YANG Hai-tian, ZHANG Xiao-yue, HE Yi-qian. Sensitivity analysis based numerical solution for truss structures with bi-modulus [J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 237-242.

[8] 吳曉, 楊立軍, 黃翀, 等. 用能量法研究雙模量大撓度圓板的軸對稱彎曲[J]. 計算力學學報, 2011, 28(2): 274-278.

WU Xiao, YANG Li-jun, HUANG Chong, et al. Large deflection axisymmetric bending of bi-modulous circular plate with energy method [J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 274-278.

[9] 吳曉, 楊立軍, 黃翀, 等. 雙模量矩形板的大撓度彎曲計算分析[J]. 工程力學, 2010, 27(1): 17-22.

WU Xiao, YANG Li-jun, HUANG Chong, et al. Large deflection bending calculation and analysis of bimodulous rectangular plate[J].Engineering Mechanics,2010,27(1):17-22.

[10] 吳曉, 楊立軍. 拉壓彈性模量不同厚壁球殼的彈性解析解[J]. 湖南科技大學學報:自然科學版, 2012, 27(4): 35-38.

WU Xiao, YANG Li-jun. Elastic solutions for thick wall spherical shell of bimodulous materials under uniform pressure [J]. Journal of Hunan University of Science & Technology:Natural Science Edition, 2012, 27(4): 35-38.

[11] 吳曉, 楊立軍, 黃翀. 雙模量圓板中心在沖擊荷載作用下的彈性計算[J]. 西安建筑科技大學學報:自然科學版, 2012, 44(5): 614-619.

WU Xiao, YANG Li-jun, HUANG Chong. Elastic dynamic calculation for bimodulous circular plate under the condition of impact load [J]. Journal of Xi’an University of Architecture & Technology:Natural Science Edition, 2012, 44(5): 614-619.

[12] 吳曉, 黃翀, 孫晉. 雙模量懸臂梁在分布荷載作用下的Kantorovich解[J]. 湖南科技大學學報:自然科學版, 2012, 27(2): 55-59.

WU Xiao, HUANG Chong, SUN Jin. The Kantorovich solution for bimodulous cantilever under distributed loads [J]. Journal of Hunan University of Science & Technology:Natural Science Edition, 2012, 27(2): 55-59.

[13] 吳曉, 黃翀, 楊立軍. 雙模量平行四邊形板彎曲的Kantorovich變分解[J]. 力學季刊, 2010, 31(4): 597-603.

WU Xiao, HUANG Chong, YANG Li-jun. Kantorovich variational solution of bending bimodulous parallelogram plate [J]. Chinese Quarterly of Mechanics, 2010, 31(4): 597-603.

[14] 姚文娟, 葉志明. 不同模量彎壓柱的解析解[J]. 應用數學和力學, 2004, 25(9): 901-909.

YAO Wen-juan, YE Zhi-ming. Analytical solution of bending-compression column using different tension-compression modulus[J]. Applied Mathematics and Mechanics, 2004, 25(9): 901-909.

[15] 姚文娟, 葉志明. 不同模量橫力彎曲梁的解析解[J]. 應用數學和力學, 2004, 25(10):1014-1022.

YAO Wen-juan, YE Zhi-ming. Analytical solution for bending beam subject to lateral force with different modulus[J]. Applied Mathematics and Mechanics, 2004, 25(10): 1014-1022.

[16] 劉相斌, 宋宏偉. 不同模量彎曲梁的自由振動[J]. 大連民族學院學報, 2007, 40(5): 104-107.

LIU Xiang-bin，SONG Hong-wei. Free vibration of the bending beam about different tensile-compressive modulus[J]. Journal of Dalian Nationalities University，2007,40(5): 104-107.

第一作者 吳曉 男，博士，教授，1965年生

摘要：研究了考慮剪切效應時雙模量梁自由振動問題。利用雙模量材料純剪切應力狀態單元體，推導出雙模量材料剪切彈性模量表達式。在考慮剪切效應的基礎上，建立雙模量梁振動的微分方程，推導出了雙模量梁振動問題的振型表達式，并討論分析了剪切效應對雙模量梁自由振動固有頻率的影響。算例分析表明，對于某些雙模量梁自由振動問題，剪切效應的影響是不能忽略的。得到了雙模量梁自由振動時，奇數波型與波型振型是不連續的存在間斷點的結論。

關鍵詞：剪切效應；雙模量；梁；自由振動；頻率

Natural vibration of bimodulous beam considering shear effect

WUXiao,HUANGZhi-gang,YANGLi-jun(Hunan University of Arts & Science, Changde 415000, China)

Abstract:Considering the shear effect, the natural vibration of a bimodulous beam was studied. The vibration differential equation of the bimodulous beam was established, the mode shapes of the bimodulous beam were derived, and the influence of shear effect on natural vibration frequencies of the bimodulous beam was analyzed. The computational results indicate that the influence of shear effect can not be ignored in some cases. The conclusion is that the odd number modal shapes of bimodulous beams are discontinuous and there are discontinuity points on the odd number type of modal waves.

Key words:shear effect; bimodulous; beam; natural vibration; frequency

基金項目：中國航空規劃建設發展有限公司資助項目(技13研-51)；國家自然科學基金資助項目(51178041)；中央高校基本科研業務費專項資金資助項目(2011JBM260)

中圖分類號:O321

文獻標志碼：A DOI:10.13465/j.cnki.jvs.2015.24.026

收稿日期：2014-10-22修改稿收到日期：2014-12-18