一種新的架空輸電線路安全限距計算模型

陳錫陽, 王艷玲, 黃　河, 張國立, 馬燕鵬

(1.廣東電網公司東莞供電局，廣東東莞523000；2.華北電力大學數理學院，河北保定071003；3.華北電力大學電氣與電子工程學院，河北保定071003)

一種新的架空輸電線路安全限距計算模型

陳錫陽1, 王艷玲2, 黃河3, 張國立2, 馬燕鵬2

(1.廣東電網公司東莞供電局，廣東東莞523000；2.華北電力大學數理學院，河北保定071003；3.華北電力大學電氣與電子工程學院，河北保定071003)

摘要：為了充分發揮輸電線路的傳送能力、減小系統限電規模，在保證線路安全運行的基礎上，達到提高經濟效益和社會效益的目的，針對架空輸電線路安全限距計算方法進行了研究，指出現有安全限距計算模型的不足，推導建立了一種新的限距計算模型，給出了求解安全限距的循環迭代算法。針對4種典型情況設計仿真實驗，比較研究了現有安全限距計算模型和所提出的限距模型。算例結果表明：所建立的限距模型更精確，所提算法是可行的、有效的，可為發揮線路最大輸送容量、科學調度提供決策參考。

關鍵詞：架空線路；弧垂；安全限距；跨越；循環迭代

中圖分類號:TM726

文獻標識碼：A

DOI:10.3969/j.issn.1672-0792.2015.02.011

收稿日期：2014-11-10。

作者簡介：陳錫陽(1972-)，男，高級工程師，研究方向為輸電線路運行維護，E-mail:zhangguoli@ncepu.edu.cn。

Abstract：In order to give full play to the transmission capacity of transmission lines, reduce the electricity supply limitation size, and achieve the purpose of promoting economic and social benefits on the basis of guaranteeing the safe operation of the lines, the research in view of the overhead transmission line security limited distance calculation method is conducted. As the limitation of the existing security limited distance calculation model is pointed out, a new mathematical model is established, and a corresponding calculation method of loop iteration is given out to calculate security limited distance accurately. Then the difference between the traditional model and newly established model is studied and compared according to four typical cases. Numerical example results show that the newly established model is more accurate than existing model, and the proposed algorithm is feasible and effective. This model can provide decision reference for taking maximum capacity of transmission lines and scientific scheduling.

Keywords：transmission line; sag; security limited distance; span; cyclic iteration

0引言

近年來，隨著經濟的快速發展，社會對電力的需求日益增長。目前電力建設相對滯后，結構性限電問題日益嚴重，并且限電規模越來越大。按照當前電網穩定控制原則，架空線路輸送容量是按“N-1”[1,2]或“N-2”控制的，因此正常運行情況下，線路的輸送能力沒有得到充分發揮，預留裕度非常大，這就導致了一方面架空線路設備利用率很低，另一方面負荷高峰期結構性限電問題突出。如果適度放寬線路的控制斷面，即可大幅減少系統限電規模，顯著提高經濟效益和社會效益。解決這一問題的前提是必需準確地計算架空線的安全限距。

架空導線安全運行的主要影響因素是導線通過一定電流后由于發熱引起的跨越物限距的變化，保持交叉跨越的足夠凈距和對地距離是送電線路安全運行必不可少的條件。因此，在輸電線路運行控制中，必須對跨越物電氣安全距離也就是安全限距進行核定，檢驗其是否滿足安全要求。事實上，隨著線路輸送容量的變化，架空線的弧垂將發生變化，進而安全限距也將隨傳輸容量動態變化，因此準確計算導線與跨越物的安全限距是非常重要和迫切的課題。導線的限距和弧垂呈現出此消彼長的關系。準確計算安全限距，一是要精確計算架空線上任一點的弧垂，另一方面是計算跨越物與架空線的最短距離。

目前關于導線弧垂的計算已有許多研究成果。對于弧垂的計算和測量主要依賴于導線的狀態方程，通過獲取導線的溫度，計算導線應力，進而計算導線弧垂[3~5]。導線溫度可以根據導線熱平衡方程計算。文獻[6]對導線隨溫度和載流量的升高引起弧垂變化進行理論分析，定量計算導線溫度上升后弧垂的增加對交叉跨越物的影響。文獻[7~8]通過圖像攝影法，利用圖像處理技術測量弧垂。文獻[9]提出了一種基于直升機巡檢時采集的航拍序列圖像進行弧垂測量的新方法。一些學者還提出基于耐張段軸向綜合張力測量、基于光纖光柵應變傳感器的弧垂實時監測方案[10~11]。文獻[12~13]將實測數據與計算方法相結合，前者通過建立輸電導線工頻電場計算模型，根據導線下方工頻電場實時測量數據，借助遺傳算法反演得到導線的弧垂；后者提出一種基于LabVIEW的弧垂計算方法，輸入現場測得的基本參數，即可快速而準確地得出線路的弧垂值。聶聳等[14]將溫度變化分解成若干個小的變溫過程進行累加求解弧垂，當鋁股應力為負時，則采用純鋼芯特性繼續求解弧垂。

在得到導線弧垂后，現有的安全限距模型都是計算導線到跨越物的豎直距離[4,15]。事實上，這樣計算出的結果只是跨越物與導線的豎直距離，不一定是最短距離。毫無疑問，安全限距需要計算的是跨越物與導線的最短距離。因此，現有的安全限距模型可能是不準確的。本文將建立一種新的限距計算模型，該模型能夠計算跨越物到導線的最短距離，從而得到準確的安全限距。

1一種新的限距計算模型及求解算法

1.1　常用的限距計算方法

目前，常用安全限距計算模型主要有2種。文獻[4]給出的限距計算公式為：

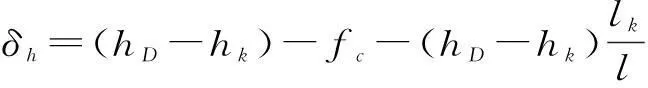
(1)

式中：δh為跨越點限距；hD，hm分別為前后懸掛點的標高；hk為跨越物高度；fc為跨越點的導線弧垂；lk為跨越點到起始桿塔的水平距離；l為跨越檔檔距。

文獻[15]利用導線應力σm和導線比載gm計算導線限距，計算公式如下：

(2)

式中：Δh為導線懸掛點高差，其余符號與式(1)中符號含義相同。

以上兩種方法雖然計算公式不同，但實際上都是計算導線到跨越物的豎直距離，并將其作為導線的安全限距。對于實際問題，安全限距應該是跨越物與架空線的最短距離，一般不是跨越物正上方的豎直距離，因此，按現有模型計算得到的安全限距可能是不準確的。本文將推導建立跨越物最高點到架空線上任一點的距離公式，給出架空線上與跨越物最高點距離最近點應滿足的條件，進而建立安全限距計算模型，并將給出相應的求解算法。

1.2　一種新的安全限距計算模型

假設桿塔、導線和跨越物在同一平面內，地面水平。以前桿頂點作為原點，前桿延長線作為y軸，平行于地面的水平線作為x軸，建立平面直角坐標系，如圖1所示。

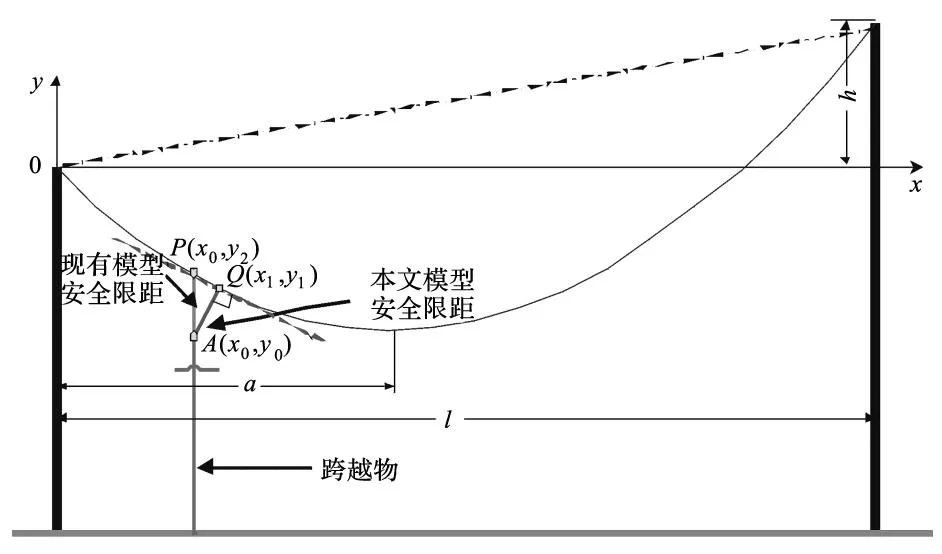
圖1　限距計算坐標系示意圖

設跨越物最高點為A(x0，y0)，現有安全限距是計算A點到跨越物豎直延長線與導線交點P(x0，y2)的距離。實際上，安全限距應該是A點到架空線的最短距離，即A點與Q點的距離。設Q的坐標為(x1，y1)。下面推導Q點應該滿足的條件，進而求出安全限距。

設架空線的懸鏈線方程為：

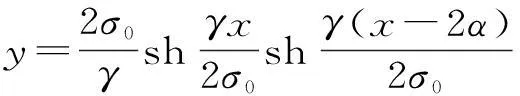
(3)

(4)

式中:l為檔距；σ0為應力；γ為比載；h為高差；(x，y)為導線上任一點的坐標；sh為雙曲正弦函數；arcsh為雙曲正弦函數的反函數；α為架空線最低點至左側低懸掛點的水平距離。

顯然，導線上坐標為(x，y)的點與跨越物最高點的距離為

求取d的最小值等價于求d2的最小值。由于此最小值一定存在且唯一，因此其最小值點必為駐點，即

解得

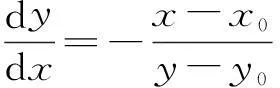
(5)

由以上推導可知，當跨越物最高點與導線上某點連線垂直于導線上此點的切線時，跨越物與導線的距離達到最小值。進一步地，由圖1可直觀地看出，|PA| ≥ |QA|/cosα，其中|PA|,|QA|指相應線段長度，α為兩條線段的夾角。而cosα≤ 1，所以線段PA長度大于QA，即現有模型所指限距大于本文指出的限距。僅當跨越物位于線路最低點正下方時，二者計算結果相等。因此可以認為現有安全限距計算模型是本文模型的一個特例。

根據分析，由式(3)、(4)、(5)得最小距離點應滿足以下條件：滿足導線方程，滿足導線的切線方程，并且此點的切線與此點與跨越物最高點連線垂直，即滿足以下方程組：

以上方程組中:(x0，y0)為已知量；(x1，y1)為待求量；其余符號含義與式(3)中含義相同。

將前3個方程代入最后一個方程可得：

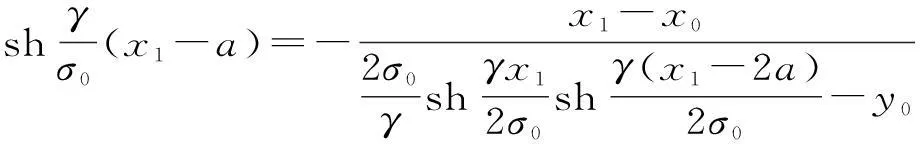
(6)

因為

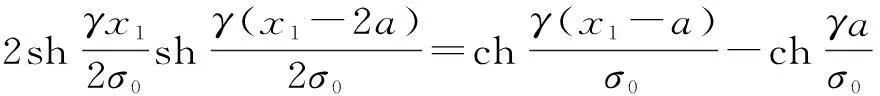
代入式(6) 可得：

x1-x0

進一步化簡如下：

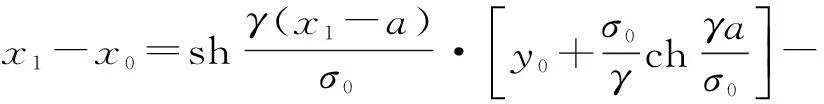
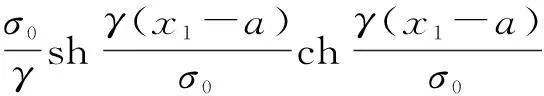
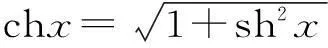
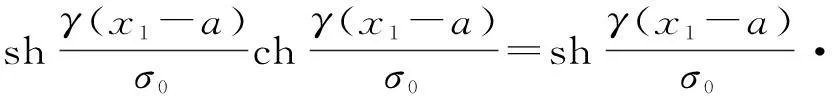
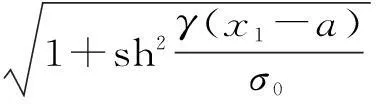
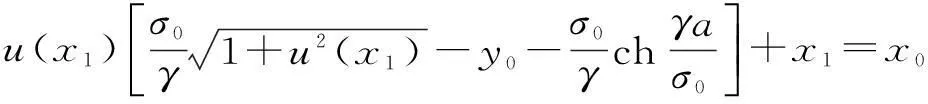
(7)

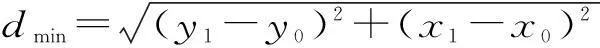
但是，式(7)是關于x1的比較復雜的非線性方程，難以求得解析解，故而考慮采用數值方法求其近似解。

1.3　循環迭代法求解最小限距

本文在新的限距計算模型下，利用循環迭代算法計算出跨越點距離導線的最短距離，以此作為導線的安全限距。

1.3.1有根區間分析

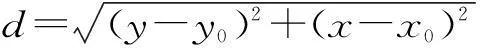
若跨越物在導線最低點右側，最低點右側懸鏈線是單調遞增函數，做同樣的分析，可知在跨越點與最低點之間存在距離的最小值對應點。

綜上所述，無論跨越物在相對于導線最低點的哪一側，在跨越點與導線最低點之間總存在距離的最小值對應點。

1.3.2算法分析與算法描述

導線上各點與跨越物最高點的距離為d，導線上任一點的橫坐標為x，由1.3.1的分析可知，最小距離點必存在于跨越點與導線最低點之間。在跨越點與導線上最低點橫坐標構成的區間上，d隨著x的增大先減后增，函數d=d(x)是一個有唯一極小值點的函數。欲求最短距離dmin，需先求最小值點x。下面給出一種循環迭代法用來求取最短距離dmin及相應的最小值點x*。

實際上，從跨越點橫坐標開始搜索，不論向左還是向右搜索，只要新點函數值小，就應該沿此方向繼續搜索，否則應該向相反方向搜索。

假設跨越物在導線最低點左側，跨越點坐標為(x0，y0)，選定跨越點橫坐標x0作為迭代初始點a0，以步長h向右搜索，即計算曲線上橫坐標為a0+h點對應的距離d1。具體說，首先利用式(8)、(9)計算曲線上橫坐標為a0，a1=a0+h點對應的縱坐標b0和b1，再按式(10)、(11)計算對應的距離d0，d1。

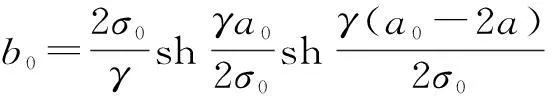
(8)

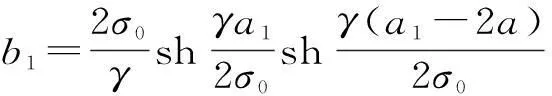
(9)

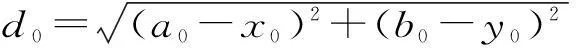
(10)

(11)

比較d0，d1，如果Δd=d1-d0<0，說明搜索方向正確，下一步繼續沿此方向搜索，否則縮短步長向相反方向搜索，直到滿足收斂準則。

按上述思想，本文給出的循環迭代算法迭代步驟如下：

①選定初始迭代點a0=x0，給定初始迭代步長h，誤差精度ε和|Δd|的容許誤差η；

②計算a1=a0+h；

③利用式(8)~(11)計算b0，b1，d0，d1；

④若|Δd|<η或h<ε，停止迭代，取x*=a1，dmin=d1，輸出結果，否則轉⑤；

⑤若Δd<0，轉⑥，否則⑦；

⑥令a0=a1，h=h，轉②；

⑦令a0=a1，h=-h/2，轉②。

由于本文所推導出的跨越物最高點到導線任一點距離的函數在有根區間內先減后增，變化趨勢較簡單，屬于典型的“單谷”函數，近似符合二次函數的特點。因此采用循環迭代法比較容易，收斂性強，并且也可以在較少的迭代次數下達到較高的精度要求。同時，考慮到學術研究與工程應用領域對計算精度的不同要求，本文算法可以通過改變誤差控制量ε和η來改變計算結果的精度。比如當ε=10-6，η=10-5時，計算結果至少可達到10-4m的精度。對于工程計算，精度要求并不是很高，就可以適度放寬誤差控制量的限制，可以在加快計算速度的同時得到符合要求的結果。

2仿真實驗

(1)首先選擇型號為JG-25導線作為研究對象，檔距l=230 m，前桿高度h1=40 m，后桿高度h2=50 m，高差h=10 m，初始溫度-5 ℃，風速15 m/s,冰厚15 mm，導線應力σ=120.15 MPa，比載γ=0.081 1 MPa/m。跨越物高度hk=10 m。

利用現有限距計算方法和本文提出的新方法分別計算導線的安全限距，研究跨越物位置不同時導線的安全限距計算結果差異。計算結果見表1。

表1　跨越物距桿塔距離不同時的限距計算結果

(2)選擇型號為JLH/G-16的導線作為研究對象，以探究導線型號不同、其他條件相同時計算結果的差異，與實驗(1)形成對比。計算結果見表2。

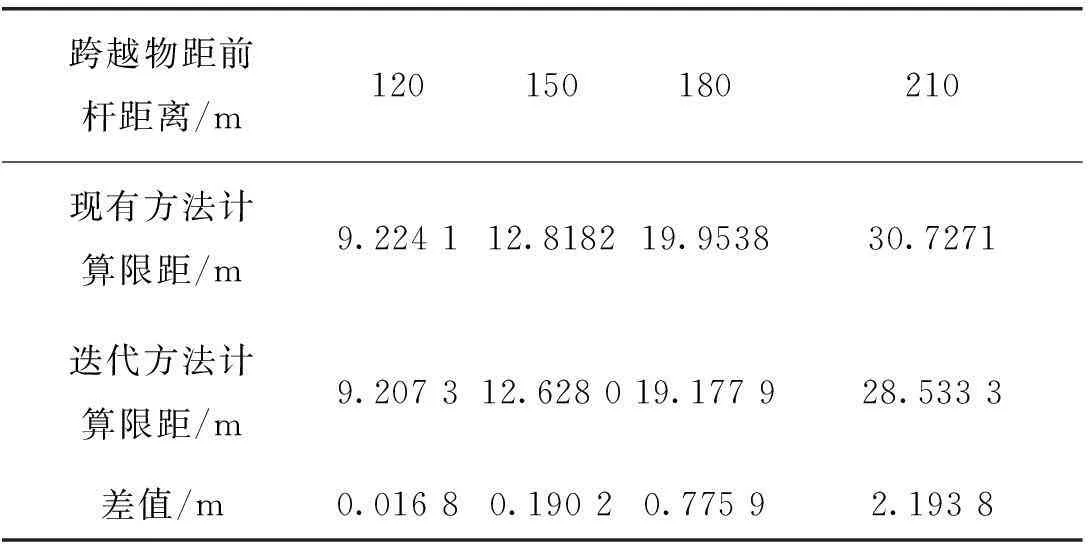
表2　更改導線型號后限距計算結果

(3)選擇型號為JLH/G-16的導線作為研究對象，以探究不同檔距、其他條件相同情況下計算結果的差異。跨越物距離前桿180 m，前桿高度h1=40 m，后桿高度h2=50 m，高差h=10 m。跨越物高度hk=10 m。計算結果見表3。

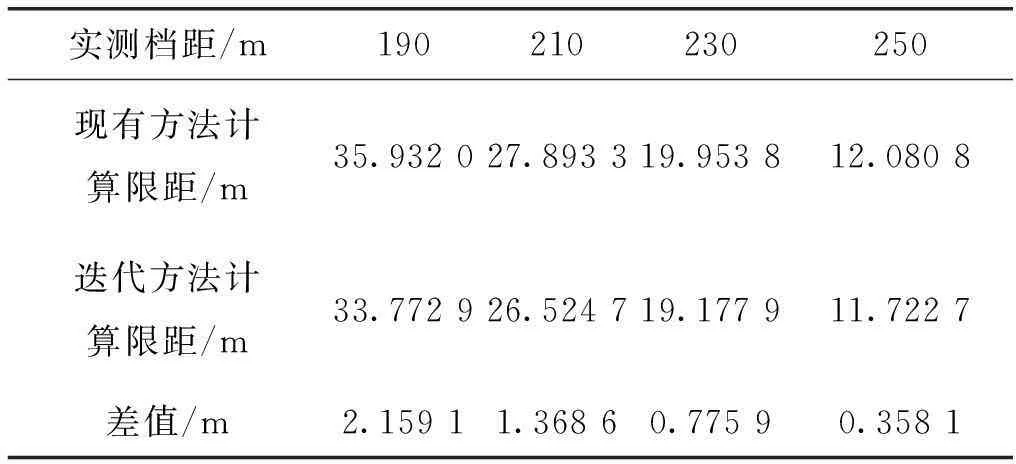
表3　檔距不同時的限距計算結果

(4)選擇型號為JLH/G-16的導線作為研究對象，以探究不同高差、其他條件相同情況下計算結果的差異。檔距l=230 m，跨越物距離前桿180 m，前桿高度h1=40 m，高差變化。跨越物高度hk=10 m。計算結果見表4。

表4　桿塔高差不同時的限距計算結果

根據以上實驗結果，可以看出，給定相同的條件，本文新模型計算的限距都要小于現有方法計算的限距，本文計算方法更加準確。

具體分析每個算例，還可以得出以下結論：

(1)由表1與表2所示計算結果可知，跨越物位置距離桿塔越近(同時也意味著距離導線最低點越遠)，現有計算方法的誤差越明顯。

(2)對比表1與表2所示計算結果可知，使用不同型號的導線計算產生的誤差不同。實驗(2)中使用的導線與實驗(1)中的相比硬度較小，架空線彎曲程度較大，使用現有方法與本文計算方法所得結果相差很明顯，尤其是在跨越物靠近后桿時，誤差已達到1 m以上，已經到了不容許忽略的地步。

(3)由表3所示計算結果可知，當其他條件一定時，改變檔距會影響計算結果的準確度。檔距越小，使用現有方法與本文計算方法所得結果相差越明顯。

(4)由表4所示計算結果可知，當其他條件一定時，改變高差會影響計算結果的準確度。高差越大，使用現有方法與本文計算方法所得結果相差越明顯。

由于安全限距會影響到導線的最大載流，本文給出更加精確的計算方法，能夠更加準確地確定導線的最大容許載流，在確保安全的前提下，提高經濟效益。

3結論

本文以架空輸電線路的安全限距為研究對象，提出一種新的限距計算模型，對模型定性分析，得出當跨越物最高點與導線上某點連線垂直于導線上此點的切線時，導線到跨越物距離達到最小值。根據此條件和導線的懸鏈線方程，推導得出了當距離達到最小值時，導線上點的橫坐標應滿足的條件，然后采用循環迭代算法進行求解，并通過算例進行了驗證，得出了比較滿意的結果。與現有限距計算方法相比，本文方法更加精確合理，計算結果更準確，可為發揮線路最大輸送容量、科學調度提供決策參考。

參考文獻:

[1]張繼楠，姜濤，賈宏杰，等．計及電力系統N-1的電壓穩定裕度估計方法[J]．電力系統及其自動化學報，2013，25(6)：1-8．

[2]蘇維波，馮彥維，陽育德．一種基于BPA數據的靜態安全最優校正分析方法 [J]．電網與清潔能源，2014，30(5)：13-27．

[3]國家電力公司東北電力設計院．電力工程高壓送電線路設計手冊[M]．北京：中國電力出版社，2003.

[4]孟遂民，孔偉．架空輸電線路設計[M]．北京：中國電力出版社，2007．

[5]周魁，徐維毅，高選，等．采用增容導線時的定位弧垂計算 [J]．電力建設，2012，33(12)：52-54．

[6]高強．架空送電線路弧垂變化對交叉跨越物距離影響的探討[J]．科技信息，2012，(33)：859,863．

[7]黃新波，張曉霞，李立涅，等．采用圖像處理技術的輸電線路導線弧垂測量[J]．高電壓技術，2011，37(8)：1961-1966．

[8]陳斯雅，王濱海，盛戈皞，等．采用圖像攝影的輸電線路弧垂測量方法[J]．高電壓技術，2011，37(4)：904-909．

[9]仝衛國，李寶樹，苑津莎，等．基于航拍序列圖像的輸電線弧垂測量方法[J]．中國電機工程學報，2011，31(16)：115-120．

[10]王孔森，盛戈皞，劉亞東，等．基于輸電線路軸向張力的導線弧垂在線監測系統[J]．華東電力， 2011，39(3)：339-343．

[11]李路明，孟小波，張治國，等．基于光纖光柵應變傳感器的架空輸電線弧垂實時監測[J]．電力建設，2011，32(7)：51-54．

[12]陳楠，文習山，藍磊，等．基于電場逆運算的輸電導線弧垂計算方法[J]．中國電機工程學報，2011，31(16)： 121-127．

[13]桂菲菲，王振剛，龐百勝，等．基于LabVIEW的架空輸電線最大弧垂計算方法[J]．電力建設，2013，34(7)：108-113．

[14]聶聳，程養春，戴沅．基于導線溫度的架空線路弧垂新算法[J]．華北電力大學學報(自然科學版)，2013，40(6)：27-32．

[15]陶凱，盧藝．實際環境下的架空導線弧垂及跨越限距工程計算[J]．南方電網技術，2010，4(5)：106-109．

A New Model to Calculate Security Limited Distance of Overhead Transmission Line

Chen Xiyang1, Wang Yanling2, Huang He3, Zhang Guoli2, Ma Yanpeng2

(1. Dongguan Power Supply Bureau, Dongguan 523000, China;2. School of Mathematics and Physics, North China Electric Power University, Baoding 071003, China;3. School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)