邊界幾何參數對空間平面張拉膜結構固有頻率影響研究
第一作者劉充男,碩士生,1989年6月生
通信作者保宏男,博士,教授,博士生導師,1971年生
邊界幾何參數對空間平面張拉膜結構固有頻率影響研究
劉充,李玉宇,保宏, 杜敬利
(西安電子科技大學電子裝備結構設計教育部重點實驗室,西安710071)
摘要:針對空間張拉薄膜陣面結構,用歸一化動態響應函數法確定薄膜邊界幾何參數對固有頻率影響關系。用Bessel函數作為薄膜橫向振動偏微分方程的解,建立任意邊界形狀凸單連通薄膜及復雜邊界薄膜固有頻率求解模型;針對平面張拉薄膜分別求解圓形、L-形、分段圓弧邊界固有頻率;分析研究一定應力條件下邊界幾何參數對薄膜固有頻率影響的內在關系。結果表明,邊界形狀導致薄膜面積減小、固有頻率增加,反之亦然。
關鍵詞:空間張拉薄膜結構;歸一化動態響應函數;固有頻率;有限元模型
基金項目:國家自然科學基金(51305321;51105290;51035006; 51175398);上海航天科技創新基金項目(SAST201413)
收稿日期:2014-07-16修改稿收到日期:2014-10-17
中圖分類號:TN957.3
文獻標志碼:A
DOI:10.13465/j.cnki.jvs.2015.20.033
Abstract:For a kind of space pre-tensioned membrane structures, a dimensionless dynamic influential function method has been proposed, which can efficiently figure out the frequencies of arbitrarily shaped, homogeneous membranes with fixed boundaries. A model using the Bessel function as the solution to the partial differential equation for transverse vibration of thin membrane was established which can be used to calculate the natural frequencies of membrane with different radius of curvature and chord length. For planar pre-tensioned membrane, the natural frequencies of membrances with circular, L-shape and subdivided arc boundary conditions were calculated. On the condition of unchanged stresses, the relationships between the natural frequencies and boundary geometrical parameters of membrane were analysed. It is indicated that the boundary which makes the area of membrane larger matches higher frequencies and vice versa.
Natural frequencies of pre-tensioned membrane structure with different boundary geometrical parameters
LIUChong,LIYu-yu,BAOHong,DUJing-li(School of Electromechanical Engineering, Xidian University, Xi’an 710071, China)
Key words:space pre-tensioned membrane structure; dimensionless dynamic influential function; natural frequency; finite element model
大型空間平面張拉膜結構因質量輕、包裝折疊效率高、易于展開等特點,廣泛用于太空可展開結構,如太陽帆、空間望遠鏡防護罩、可展開反射陣列天線等。周邊索網張拉薄膜結構,見圖1、圖2。該結構由支撐桿、張拉懸索、平面薄膜組成,其中,張拉懸索包括外懸索、牽連索、內懸索。
針對該類型張拉薄膜結構,Sakamoto[1]理論上證明薄膜外形為圓弧狀時膜內應力為最佳張緊狀態,能有效避免褶皺產生;并研究該結構在膜、索給定應變條件下內外懸索截面積、索膜總質量隨圓弧數目變化的函數關系。Park等[2]研究該結構的魯棒性、分析膜面褶皺對固有頻率影響認為,在角點支撐發生面內位移情況下外索能有效抑制角點位移向膜面內傳播。Leifer等[3]用ANSYS分析薄膜邊界剪切變形下褶皺出現臨界條件及褶皺幅值、波數。Tessler等[4]研究由薄膜結構中索、膜大變形產生的幾何非線性,并用薄殼屈曲理論分析褶皺幅值。汪有偉等[5]研究力與邊界弧長數奇偶性質關系,分別給出優缺點。
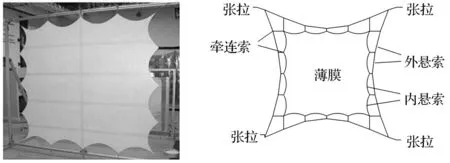

圖1 索網張拉陣面天線原理樣機Fig.1Thephotoofthemembranearrayantenna圖2 周邊索網張拉薄膜結構示意圖Fig.2Web-cablegirdedmembranestructure
以上對周邊索網張拉薄膜結構研究多集中于幾何參數優化及薄膜在軌工作表面精度(褶皺),而有關結構參數對固有頻率影響研究較少,薄膜固有頻率為反映結構魯棒性及保證形面精度的重要指標。
Kang等[6-8]提出歸一化動態響應函數法,建立任意凸邊界形狀薄膜固有頻率求解模型及多域法模型,可求解凹陷邊界或區域內部不連續薄膜固有頻率并推廣到任意邊界形狀板固有頻率求解。然而,該方法假設薄膜任意點受力相同,均為二軸等值拉伸應力狀態,理論計算不存在任何問題,而工程應用中并非任何邊界形狀膜可實現此應力狀態。
為此,本文提出分段圓弧狀邊界膜,通過邊界索管道式張拉,理論上可實現均勻應力狀態;并針對周邊索網張拉薄膜結構,研究索膜在一定應力水平下結構參數對薄膜固有頻率影響。
1任意邊界形狀薄膜振動模型
1.1凸單連通區域薄膜振動模型
1.1.1歸一化動態響應函數
研究任意固定邊界形狀薄膜固有頻率,設薄膜:①處于均勻二軸等值拉伸應力狀態;②不承受任何彎矩、剪切;③材料均勻各向同性,且面內變形較小,滿足Hooker定律;④面內張拉剛度遠大于橫向幾何剛度,忽略面內振動。
考慮任意形狀均勻薄膜,單位面積質量為ρ,單位長度張力為T,變形前完全處于xoy平面,見圖3虛線。
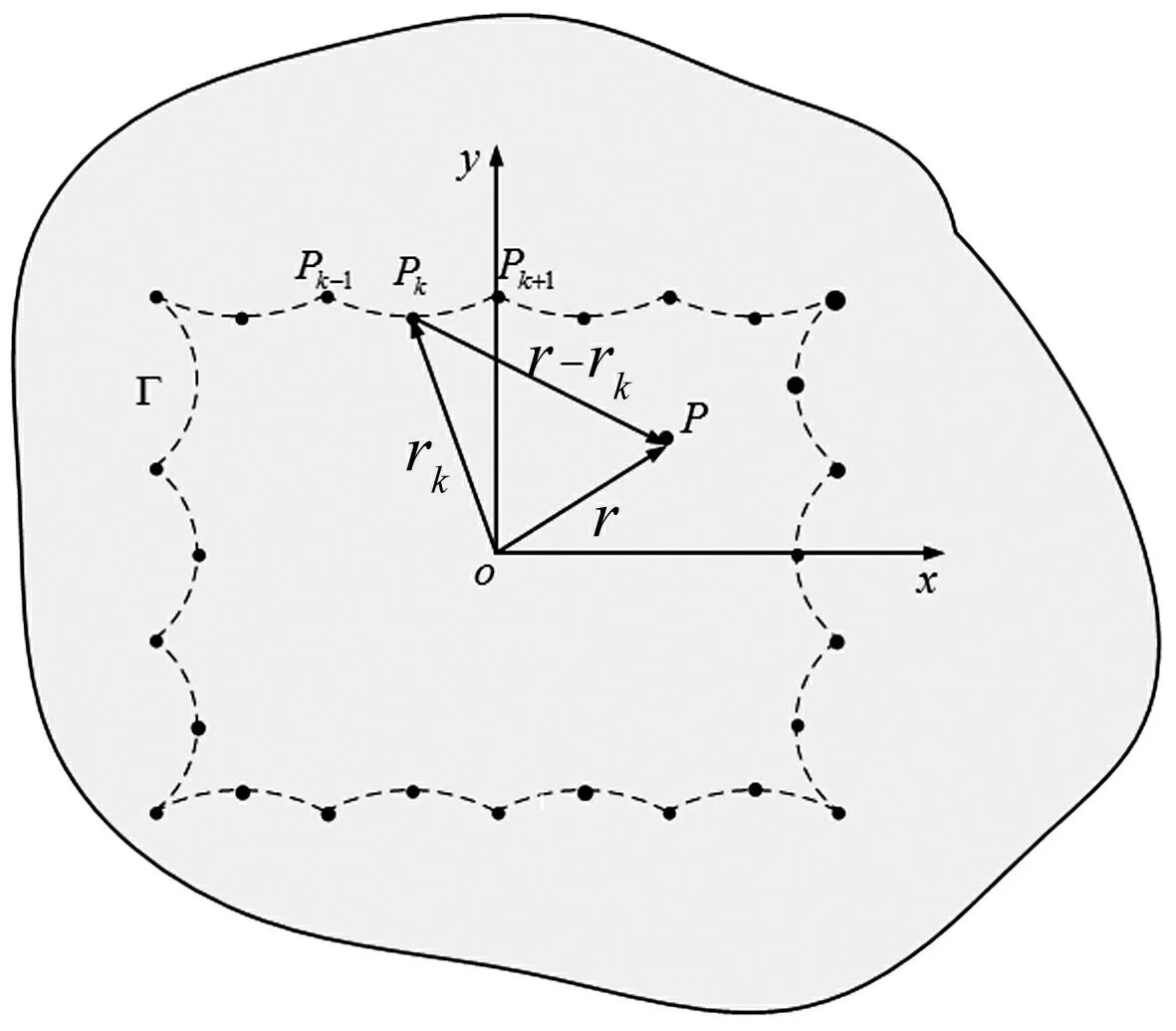
圖3 任意邊界形狀薄膜 Fig.3 Arbitrarily shaped membrane
對該膜邊界Γ進行小位移u(rΓ,t)諧波激勵,其中rΓ為邊界任意點位置矢量。用w(r,t)表示薄膜在t時刻橫向位移,其中r為薄膜任意點位置矢量,則其橫向振動偏微分方程及邊界條件[9]分別為
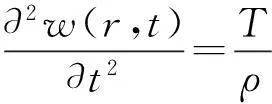
(1)
w(rΓ,t)=u(rΓ,t)
(2)
對諧波激勵,用分離變量法將w(r,t)、u(rΓ,t)寫為
w(r,t)=W(r)ejωt
(3)
u(rΓ,t)=U(rΓ)ejωt
(4)
式中:ω為激勵源角頻率。
代入式(1)、(2)得
2W(r)+Λ2W(r)=0
(5)
W(rΓ)=U(rΓ)
(6)
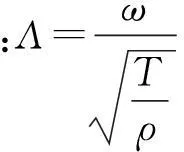
式(5)為Helmholtz方程,坐標變換后可得Bessel方程,基本解為Bessel函數,α階Bessel函數表達式[10]為
引入歸一化動態響應函數為
(7)
式中:ω為激勵源角頻率;r,rk分別為點P,Pk位置矢量;J0(x)為零階第一類Bessel函數。
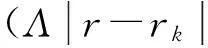
式(6)為連續邊界條件,若將薄膜邊界離散化,即用諸多離散點Pi(i=1,2,…,N)表示邊界,則可得對應式(6)的離散邊界條件為
W(ri)=U(ri),(i=1,2,…,N)
(8)
當離散點個數N趨于無窮時,式(8)則會收斂為式(6)。
1.1.2任意固定邊界薄膜方程
在無限大薄膜上選一條與實際薄膜有相同位置、形狀虛構邊界(圖3),沿邊界分配N個點。若P1,P2,...,PN做簡諧振動,設振幅為A1,A2,…,AN,通過線性疊加,點P總位移響應計算式為
(9)
利用式(8)可得
(10)
寫成矩陣形式為
SM(Λ)A=U
(11)
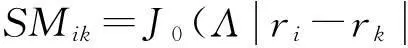
等式(11)稱為系統矩陣方程。對于周邊固定薄膜的自由振動分析,式(11)中令U=0,得
SM(Λ)A=0
求解det[SM(Λ)]=0可得系統特征值即結構固有頻率,薄膜相應模態由式(9)獲得。至此,可求解任意幾何邊界形狀薄膜固有頻率。
1.2復雜邊界形狀薄膜振動模型
用單域法求解具有凹陷或含孔洞薄膜固有頻率時計算結果往往不收斂,此因歸一化動態響應函數為波形函數,考慮無限區域時會從一點沿全方位傳播,而薄膜凹陷或孔洞區域會隔斷波直線傳播,因此單區域法求解得不到正確結果。

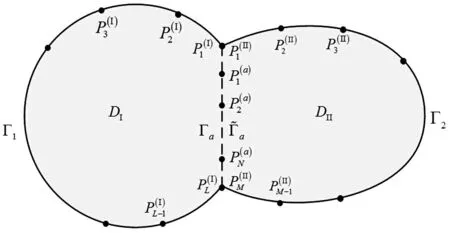
圖4 凹陷薄膜被分成兩子區域 Fig.4 Concavely shaped membrane subdivided into two domains
對兩子區域分別用歸一化動態響應函數單區域法獲得系統矩陣方程分別為
SMⅠAⅠ=UⅠ
(12)
SMⅡAⅡ=UⅡ
(13)
或寫成
(14)
(15)
亦可寫為
SM11A1+SM1aAa=U1
(16)
SMa1A1+SMaaAa=Ua
(17)
(18)
(19)
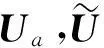
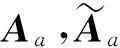
(20)
(21)
分別代入式(17)、(19),且在邊界Γa上滿足
(22)
(23)
式中:n為公共邊界法線方向,該凹陷薄膜在公共邊界法線方向上C1連續。
將式(17)、(19)代入式(22)、(23)得
SM(Λ)A=0
(24)
系統矩陣SM(Λ)、向量A表達式為
SM=
(25)
(26)
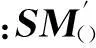
同理,可導出歸一化動態響應函數三、四等多區域法,據薄膜邊界形狀合理劃分區域,求出具有凹陷或含孔洞薄膜固有頻率及模態。
2計算實例
2.1算例1:圓形薄膜固有頻率
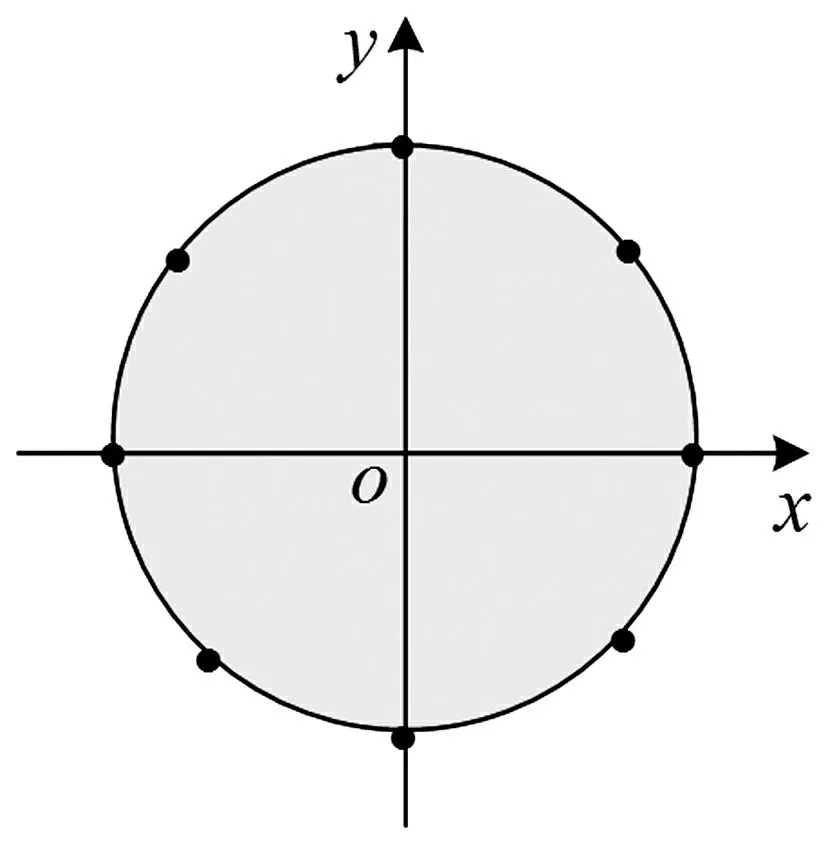
圖5 圓形薄膜 Fig.5 The circular membrane
圓形邊界薄膜固有頻率存在理論解,本文分別用歸一化動態響應函數單區域法及有限元法求解,并與理論解對比。選半徑為單位1的均勻圓形薄膜,見圖5,在邊界上分別等間距取8,12,16點。
歸一化動態響應函數法中,系統矩陣行列式值的對數隨系統特征值Λ變化關系見圖6,極值點橫坐標為薄膜固有頻率。
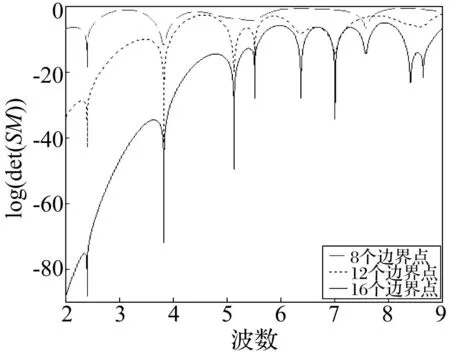
圖6 圓形薄膜特征值 Fig.6 The eigenvalues of circular membrane
三種方法結果見表1。由表1看出,用歸一化動態響應函數法求解結果非常精確,隨邊界點數增加收斂于理論解。取8或12個邊界點時系統方程階數較低,無法獲取前八階全部固有頻率。而有限元法將無限自由度結構離散成有限自由度結構,增大結構剛度,故求解的固有頻率值大于理論解。隨單元劃分細化,有限元解收斂于理論解。該算例表明歸一化動態響應函數法對固定邊界薄膜固有頻率求解收斂性、精確性良好。
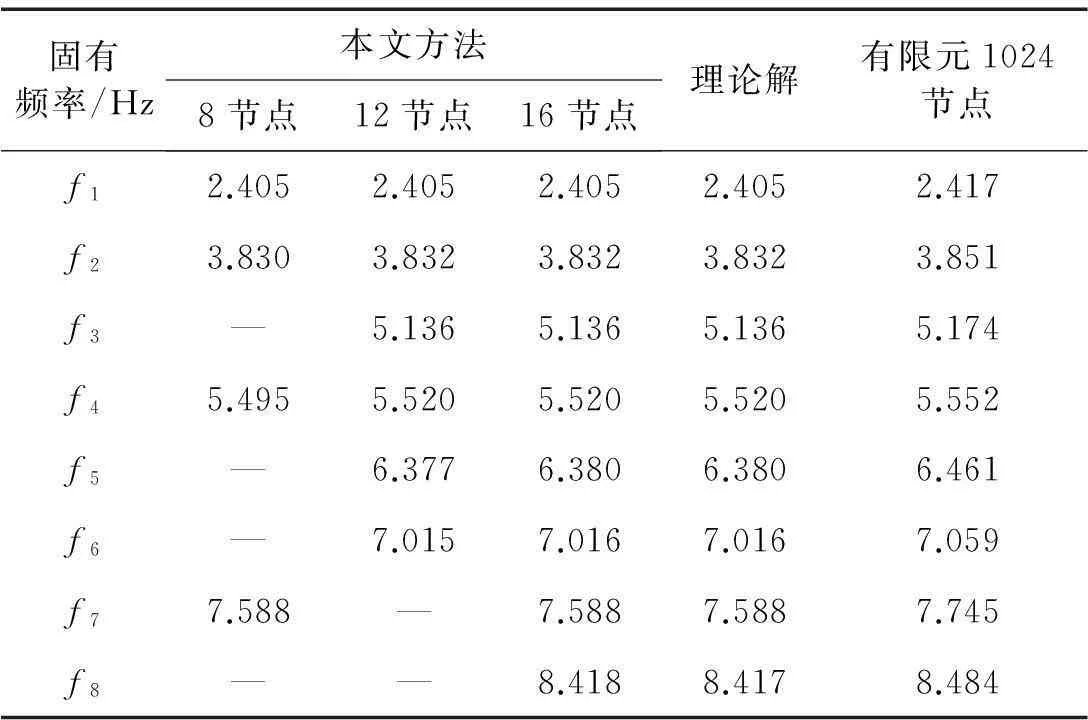
表1 圓形薄膜固有頻率
2.2算例2:L-形薄膜固有頻率
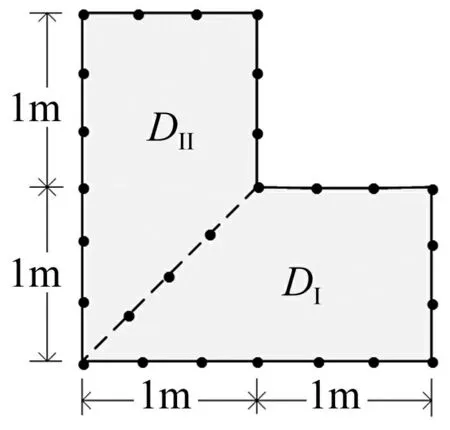
圖7 L-形薄膜(單位:m) Fig.7 The L-shape membrane
L-形薄膜固有頻率不存在理論解,本文分別用歸一化動態響應函數多區域法及有限元法求解,將兩結果對比,表明多區域法的有效性。將L-形薄膜分成兩子區域,在公共邊界取3個離散點,固定邊界取24個離散點,見圖7。
歸一化動態響應函數兩區域法中,系統矩陣行列式值的對數隨系統特征值Λ變化關系,如圖8,極小值點的橫坐標表示薄膜的固有頻率。
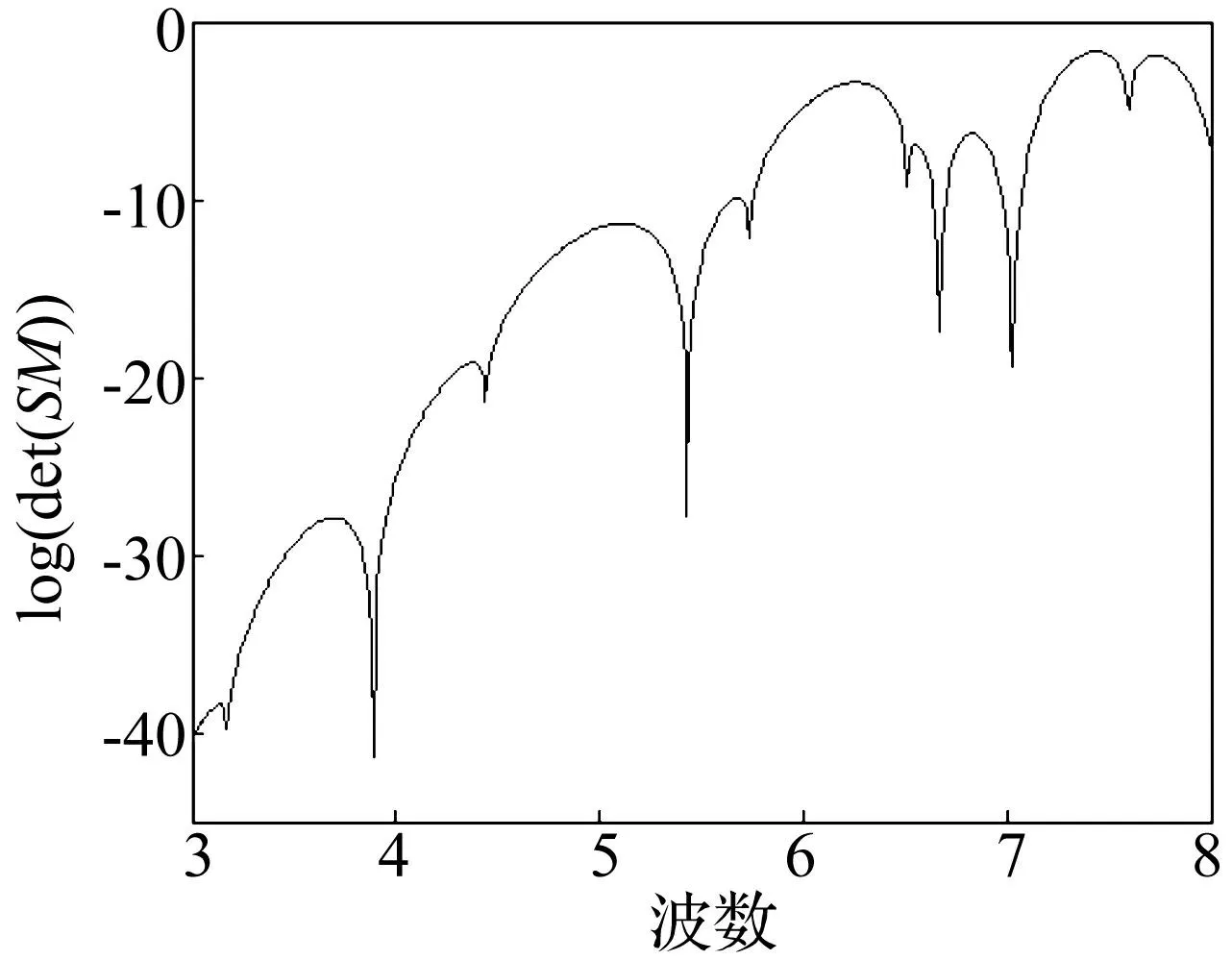
圖8 L-形薄膜特征值 Fig.8 The eigenvalues of L-shape membrane
兩區域法與有限元法結果見表2。由表2看出歸一化動態響應函數多區域法的有效性與準確性。與有限元法相比,多區域法計算所需節點數目較少,且計算中無需數值積分,計算量大大減少。
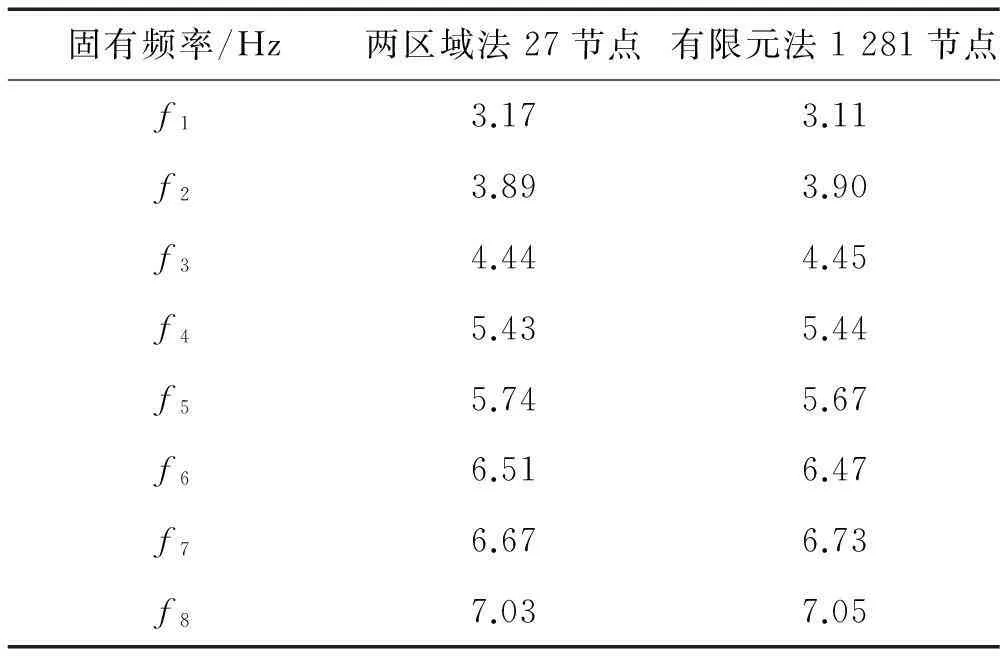
表2 L-形薄膜的固有頻率
2.3算例3:圓弧狀薄膜固有頻率
周邊索網張拉薄膜結構中薄膜部分見圖9,各邊界等份若干段圓弧。其中l1=20m,l2=4m為薄膜長、高;N1,N2為薄膜長、高邊界圓弧段數;θ1,θ2為長、高上圓弧圓心角。
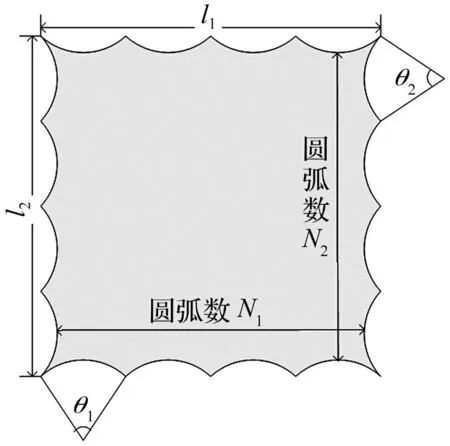
圖9 圓弧狀固定邊界薄膜 Fig.9 Shapes of circular segments of a membranewith fixed boundary
薄膜受均勻二軸等值拉伸應力T=1 440 Pa,材料參數見表3。

表3 材料參數
保持條件θ1=θ2=10°,N2=4不變前提下改變長邊分段數,用多域法所得薄膜固有頻率見表4。由表4看出,隨長邊圓弧段數增加薄膜面積變大,薄膜固有頻率降低。同理,保持條件N1=20,N2=4,θ2=10°不變前提下改變長邊圓弧圓心角,用多域法所得薄膜固有頻率見表5。由表5看出,隨圓心角增大薄膜面積減小,薄膜固有頻率增大。

表4 薄膜固有頻率隨長邊弧長數目變化關系
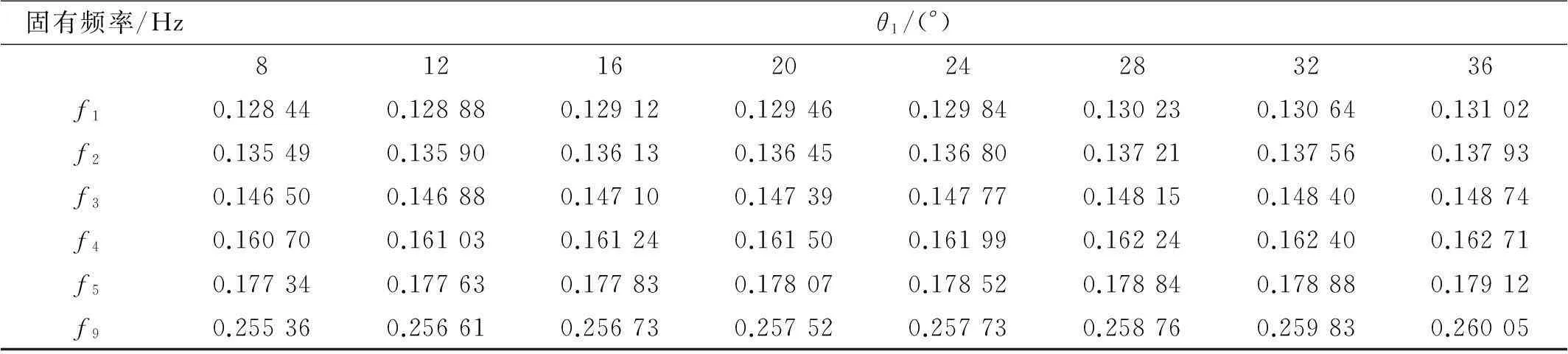
表5 薄膜固有頻率隨長邊弧長圓心角變化關系
3結論
(1)利用歸一化動態響應函數法求解任意形狀固定邊界薄膜固有頻率,給出高效、精確求解薄膜固有頻率方法,計算所需節點數遠少于有限元方法。
(2)對復雜薄膜邊界,所提多域法可有效彌補單域法不足。對周邊索網張拉結構薄膜給出固有頻率及邊界結構參數(曲率半徑、弦長)變化關系。
參考文獻
[1]Sakamoto H. Dynamic wrinkle reduction strategies for membrane structures[D]. Colorado: University of Colora-do, 2004.
[2]Sakamoto H,Park K C. Evaluation of membrane structure designs using boundary web cables for uniform-tensioning [J].ActaAstronautica,2007(60):846-857.
[3]Leifer J, Belvin W K. Prediction of wrinkle amplitudes in thin film membranes using finite element modeling[C].The 44thAIAA/ASME/ASCE/AHS Structures, Structural Dyna-mics and Material Conference, Norfolk, Virginia, 2003.
[4]Tessler A, Sleight D W, Wang J Y. Nonlinear shell modeling of thin membrane with emphasis on simulation wrinkling[C].The 44thAIAA/ASME/ASCE/AHS Structures, Structural dynamics, and material Conference, Norfolk, Virginia, 2003.
[5]汪有偉,關富玲,韓克良,等.內外部懸索聯合張拉膜結構的設計與分析[J]浙江大學學報:工學版,2010,44(6): 1213-1219.
WANG You-wei,GUAN Fu-ling,HAN Ke-liang,et al. Design and analysis of inner and outer cables suspendded membrane structures[J].Journal of Zhejiang University: Engineering Science,2010,44(6):1213-1219.
[6]Kang S W, Lee J M, Kang Y J. Vibration analysis of arbitrarily shaped membranes using non-dimensional dynamic influence function[J]. Journal of Sound and Vibration,1999, 221:117-132.
[7]Kang S W, Lee J M. Application of free vibration analysis of membranes using the non-dimensional dynamic influence function[J].Journal of Sound and Vibration,2000, 234(3):455-470.
[8]Kang S W,Lee J M. Free vibration analysis of arbitrarily shaped plates with clamped edges using wave-type functions[J].Journal of Sound and Vibration,2002, 242(1): 9-26.
[9]林文鏡,陳樹輝,李森.圓形薄膜自由振動的理論解[J].振動與沖擊,2009,28(5):84-86.
LIN Wen-jing,CHEN Shu-hui,LI Sen.Analytical solution of the free vibration of circular membranc[J]. Journal of Vibration and Shock, 2009,28(5):84-86.
[10]倪致祥. 數學物理方法[M].合肥:中國科學技術大學出版社,2012.


