制冷劑管道參數對冰箱振動影響特性

第一作者孔祥強男，博士，副教授，1976年生

郵箱：kxqiangly@126.com

制冷劑管道參數對冰箱振動影響特性

孔祥強，陳麗娟，李瑛

(山東科技大學機械電子工程學院，山東青島266590)

摘要：為減小冰箱振動、降低噪聲，利用Pro/Engineer軟件分別建立冰箱制冷劑管道內部氣柱及管道三維實體模型，用有限元分析軟件ANSYS分析模態，獲得氣柱及管道固有頻率。氣柱固有頻率與壓縮機激發頻率相差較大不會產生共振，而管道固有頻率在共振區內會產生共振。在制冷劑管道材料不變條件下分析不同管道長度、彎管圓角半徑及固定支撐位置對冰箱振動特性影響。結果表明，減小制冷劑管道長度會增大固有頻率并逐漸遠離共振區，從而避免管道共振；增加制冷劑管道彎管圓角半徑，其固有頻率略有增大，一階固有頻率仍在共振區內導致管道共振；在制冷劑管道不同位置增加固定支撐，能有效提高管道固有頻率，使其遠離共振區，且存在最佳安裝位置。

關鍵詞：冰箱；制冷劑管道；振動；模態分析；固有頻率

基金項目：山東省高等學校科技計劃資助項目(J11LD63)；山東省泰山學者建設工程專項經費資助項目;青島市黃島區科技項目(2014-1-40)

收稿日期：2014-08-01修改稿收到日期：2014-09-30

中圖分類號:TB535

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.20.035

Abstract:In order to reduce the vibration and noise of a refrigerator, geometric models of the refrigerant pipe and the gas column in the pipe were created respectively by using Pro/Engineer software, and natural frequencies of the pipe and the gas column were obtained by the modal analysis based on ANSYS software. It is found that gas column resonance will not appear due to the large difference between compressor excitation frequency and the gas column natural frequency, but pipe resonance will occur when the pipe natural frequency is in the resonance zone. The vibration characteristics of the pipes mode of the same material yet with different length, fillet radius and support location were analyzed. The model analysis results show that, the pipe natural frequency increases continuously and gets far away gradually from the resonance zone with the decrease of refrigerant pipe length. The pipe natural frequency is slightly getting higher with the increase of fillet radius, however the pipe resonance will still occur with the first order natural frequency in the resonance zone. The pipe natural frequency can be improved effectively and get far away from the resonance zone by adding supports in different locations, and a best location exists.

Influence of refrigerant pipe parameters on vibration characteristics of refrigerator

KONGXiang-qiang,CHENLi-juan,LIYing(College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao 266590, China)

Key words:refrigerator; refrigerant pipe; vibration; modal analysis; natural frequency

電冰箱作為廣大家庭不可或缺的電器運行時噪聲大小頗受關注，并與節能、環保同為評定家電產品質量優劣的三大要素。因而國標[1]對冰箱、空調、洗衣機、微波爐、吸油煙機及電風扇等6類家電噪聲限值進行明確規定。其中，冰箱容積<250 L的噪聲值不超過45 dB，容積>250 L的噪聲值不超過48 dB。

對冰箱降噪已有諸多研究。如Gue等[2]通過對冰箱風扇噪聲試驗研究及數值模擬提出低噪聲風扇設計方案。Seo等[3]利用穿孔板結構降低冰箱風扇噪聲。褚志剛等[4]設計出冰箱風扇振動質量在線檢測系統。陳建良等[5]對冰箱壓縮機殼體輻射噪聲進行數值分析。仲崇明等[6]對冰箱往復式壓縮機振動進行有限元數值模擬，驗證其用于振動響應分析的可行性。郭維等[7]用錘擊脈沖激勵法對冰箱壓縮機殼進行試驗模態分析，獲得整機殼體振動特性。趙科等[8]對冰箱用動磁式直線壓縮機的動態特性進行仿真。

以上研究主要集中于冰箱風扇及壓縮機降噪，而冰箱內部制冷劑管道振動對冰箱噪聲亦有較大影響。管道振動主要由內部氣流脈動引起，壓縮機為冰箱內部制冷劑管道振動激發源。Kim等[9]通過測量冰箱壓縮機排氣管試驗模型的氣流脈動認為，氣流脈動與噪聲間存在一定關系。Lee等[10]試驗研究冰箱壓縮機管道的振動特性。劉益才等[11]通過研究冰箱毛細管出口處噴射噪聲，獲得湍流強度、壓力及流速沿流動方向變化及流場分布特性。Han等[12]通過改變蒸發器入口管形狀及布局，使冰箱輻射噪聲在315～3 150 Hz頻率范圍內減少約2～5 dB。李春銀等[13]用有限元分析軟件對空調旋葉式壓縮機排氣閥片進行模態分析，獲得排氣閥片振動特性。

用有限元分析軟件對冰箱制冷劑管道進行模態分析研究較少。為此，本文基于多自由度系統振動微分方程，用有限元軟件ANSYS對冰箱局部制冷劑管道進行模態分析，計算管道系統固有頻率，獲得管道結構參數對冰箱振動的影響特性。

1制冷劑管道系統數學模型

氣流脈動引起的管道振動非常復雜，且存在兩振動系統，即氣柱及管道機械振動系統[14]。制冷劑管道內部充滿氣體稱為氣柱，由于氣體可壓縮膨脹，可將氣柱視為有連續質量的彈簧振動系統，具有固有頻率及振型，氣柱受壓縮機周期性吸排氣激發會產生振動；而管道本身也具有固有頻率，只要激發源作用于管道，則會產生機械振動響應。此兩種均為多自由度振動系統，其振動微分方程為一組互相耦合的常微分方程組，直接求解、分析較困難[15]。為此，本文采用模態分析方法分析求解。

1.1管道內部氣柱固有頻率計算數學模型

管道內部氣柱固有頻率常采用轉移矩陣法計算，但轉移矩陣法建立在一維數學模型基礎上，用于計算管道內部氣柱固有頻率較繁瑣且精度不高。本文用模態分析方法計算冰箱制冷劑管道內部氣柱固有頻率。

設制冷劑氣體無粘性、可壓縮；氣體平均密度、壓力、速度均為定值；介質中傳播為小振幅聲波。

氣柱聲學波動方程[16]為

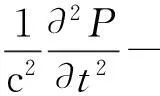
(1)

式中：▽2為拉普拉斯算子；c為氣體聲速；P為氣體聲壓；t為時間。

利用微分方程等效積分形式并結合加權余量法的伽遼金(Galerkin)法，對管道內部氣柱振動系統建立有限元方程為

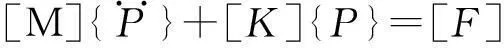
(2)

式中：[M]，[K]分別為氣柱質量、剛度矩陣；{P}為壓力向量；[F]為管道內部氣柱所受載荷矩陣。

設式(2)中[F]=0，即管道氣柱固有頻率數學模型為

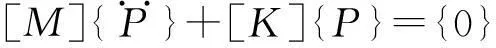
(3)

1.2管道固有頻率計算數學模型

冰箱制冷劑管道系統振動微分方程為

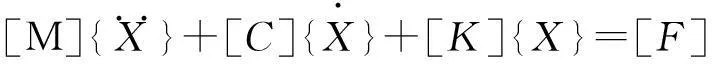
(4)

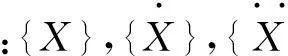
設式(4)中[C]，[F]均為0，即為管道固有頻率數學模型

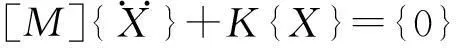
(5)

2壓縮機激發頻率

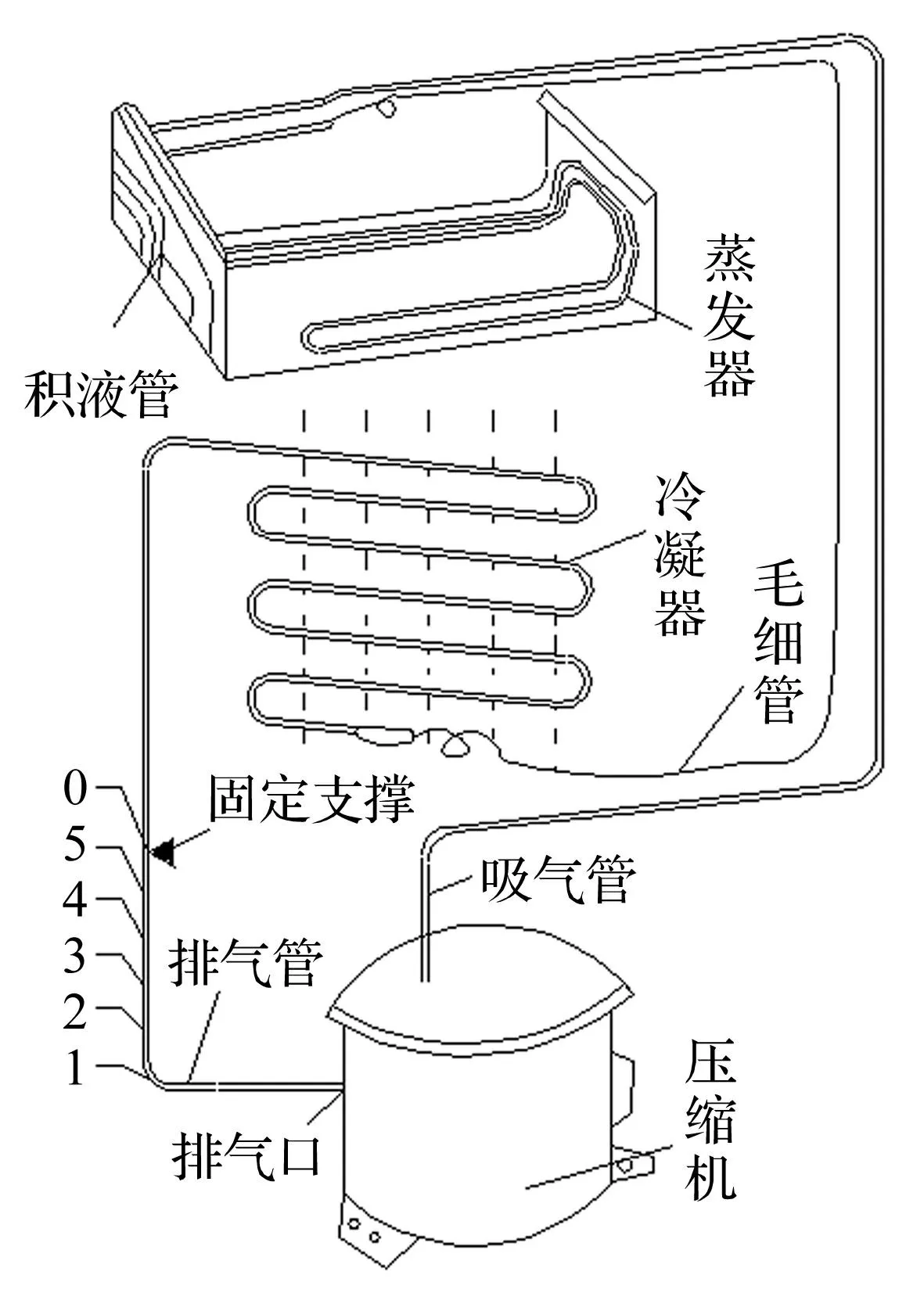
圖1　冰箱內部結構示意圖 Fig.1 Schematic diagram of refrigeration system

冰箱制冷系統內部結構見圖1。采用單級活塞式制冷壓縮機，工作轉速3 000r/min；管式蒸發器，材料銅鋁合金，總長14.96 m，外徑8 mm，壁厚0.6 mm；翹片管式冷凝器，材料表面鍍鋅鋼管，長8.76 m，外徑9.52 mm，壁厚0.35 mm；制冷劑管道、冰箱殼體全部用螺釘固定；0點位置為排氣管原有固定支撐點，1～5點分別為新設不同固定支撐添加位置。

冰箱管道振動激發源為壓縮機，激發頻率算式為

(6)

式中：n為壓縮機轉速；i為壓縮機作用方式，對單級制冷壓縮機i=1；m為簡諧階次。

壓縮機激發頻率計算結果見表1。

表1　壓縮機激發頻率

3管道內部氣柱固有頻率

壓縮機周期性吸排氣會激發其相連管道振動，為獲得管道參數對冰箱振動影響規律，以圖1壓縮機排氣口及固定支撐間制冷劑管道為分析對象。該管道長900 mm，彎管圓角半徑30 mm，管道內部制冷劑熱物理參數設為：壓力1.8 MPa，溫度50 ℃，制冷劑氣體密度2.544 kg/m3，聲速340 m/s。利用Pro/E建立管道內部氣柱三維模型，再導入ANSYS進行模態分析。選ANSYS流體分析模塊，單元類型選三維聲單元，冰箱管道內氣柱有限元模型見圖2。

圖2　管道內部氣柱有限元模型 Fig.2 Finite element model of gas column in pipe

計算得管道內氣柱固有頻率見表2。由表2看出，管道內氣柱固有頻率較小，與壓縮機激發頻率差距較大。因此氣柱不會發生共振及由此產生強烈噪聲。

表2　管道內部氣柱固有頻率

4管道固有頻率

冰箱內部制冷劑管道為連續彈性體結構，具有無窮多自由度及固有頻率。系統固有頻率作為結構的固有屬性，其大小只與結構質量、剛度有關，與外載荷無關[17]。如果冰箱管道結構設計不合理，其固有頻率會接近壓縮機激發頻率基頻或倍頻，使壓縮機運行頻率范圍內出現管道系統固有模態，導致管道產生共振。

仍以壓縮機排氣口與固定支撐間局部制冷劑管道為分析對象，管道有限元模型見圖3。計算所得管道固有頻率見表3。

表3　管道固有頻率

圖3　管道有限元模型 Fig.3 Finite element model of pipe

固有頻率為激發頻率的0.8～1.2倍(即共振區)時管道會發生共振。管道固有頻率與共振區關系見圖4。由圖4看出，一階固有頻率落在共振區內，五階靠近共振區，此時管道將發生共振，且以較大振幅強烈撞擊冰箱殼體，繼而產生較大噪聲。因此，本文通過改變管道長度、彎管處圓角半徑及添加固定支撐等進行優化設計，能避免或防止共振發生，達到降噪聲目的。

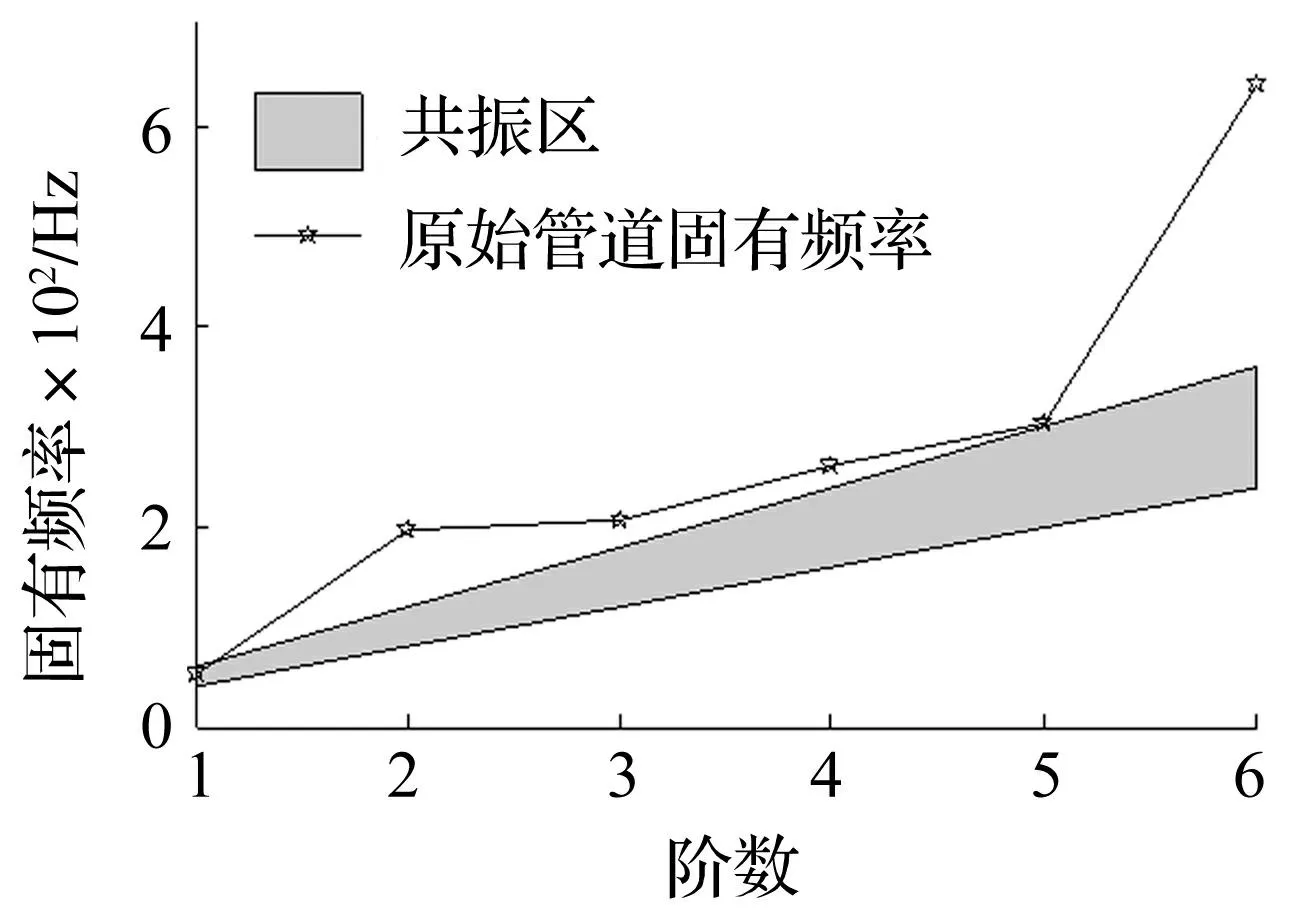
圖4　管道固有頻率與共振區 Fig.4 Natural frequency of pipe and resonance region

4.1管道長度對固有頻率影響

管道長度分別取700 mm、800 mm、900 mm、1 000 mm及1 100 mm五組數據，固有頻率計算結果見圖5。由圖5可見，隨管道長度增加固有頻率減小；長度由900 mm增到1 000 mm時，其一階～五階固有頻率均落在共振區；長度為1 100 mm時固有頻率全部落在共振區；長度減小到800 mm或700 mm時固有頻率遠離共振區，且隨長度減小固有頻率增大，因而能有效避免共振發生。減小管道長度可使固有頻率與壓縮機激發頻率錯開，既能避免共振又能降低管道振動及噪聲。

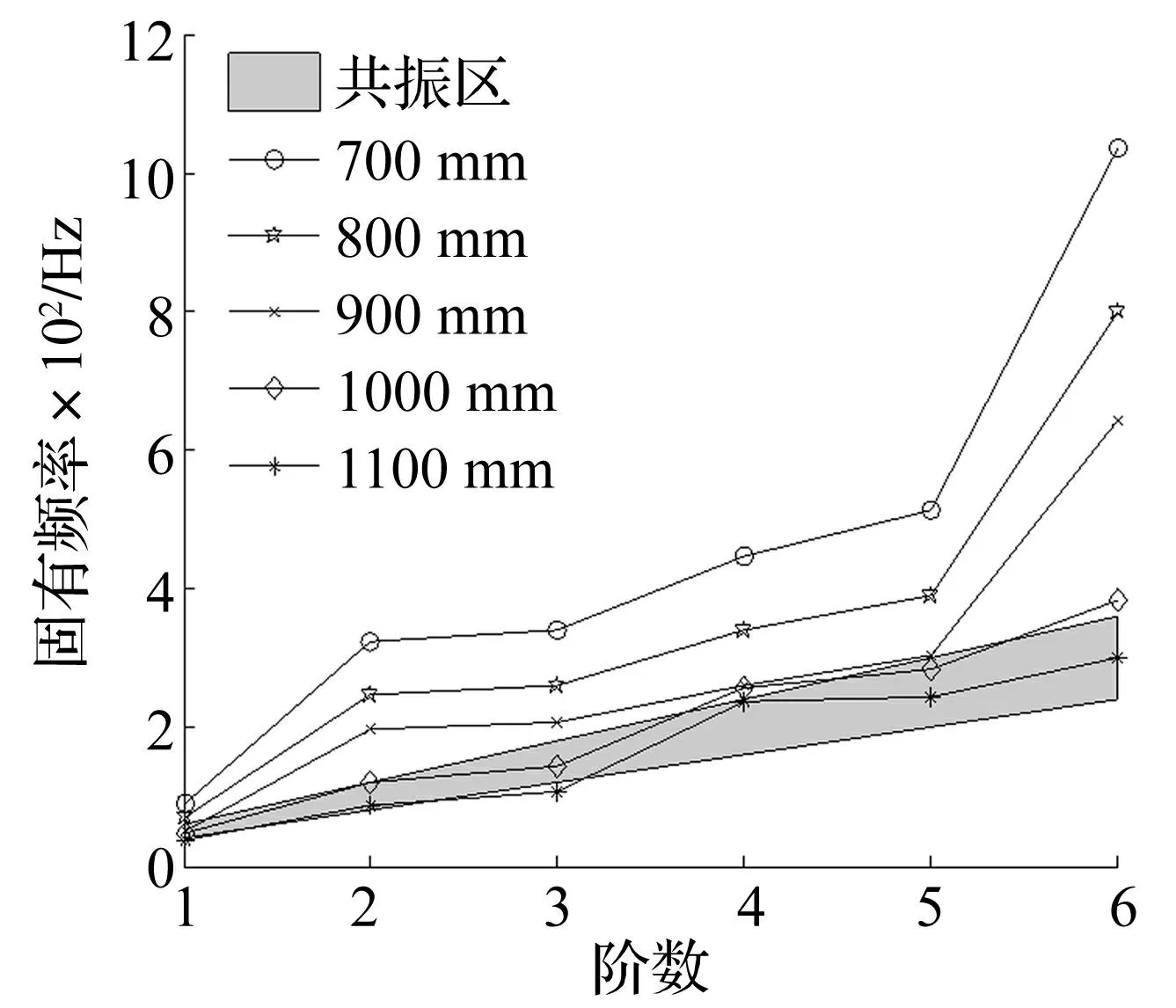
圖5　管道長度對固有頻率影響 Fig.5 Effect of length on pipe natural frequency

4.2彎管圓角半徑對管道固有頻率影響

管道其它結構參數不變條件下，彎管圓角半徑分別取20 mm、30 mm、40 mm、50 mm及60 mm。計算所得管道固有頻率與共振區關系見圖6。由圖6可知，隨圓角半徑增加管道固有頻率略有增大，但增幅較小。圓角半徑增大到60 mm時管道一階固有頻率仍落在共振區。故改變彎管圓角半徑不能達到減振降噪目的。

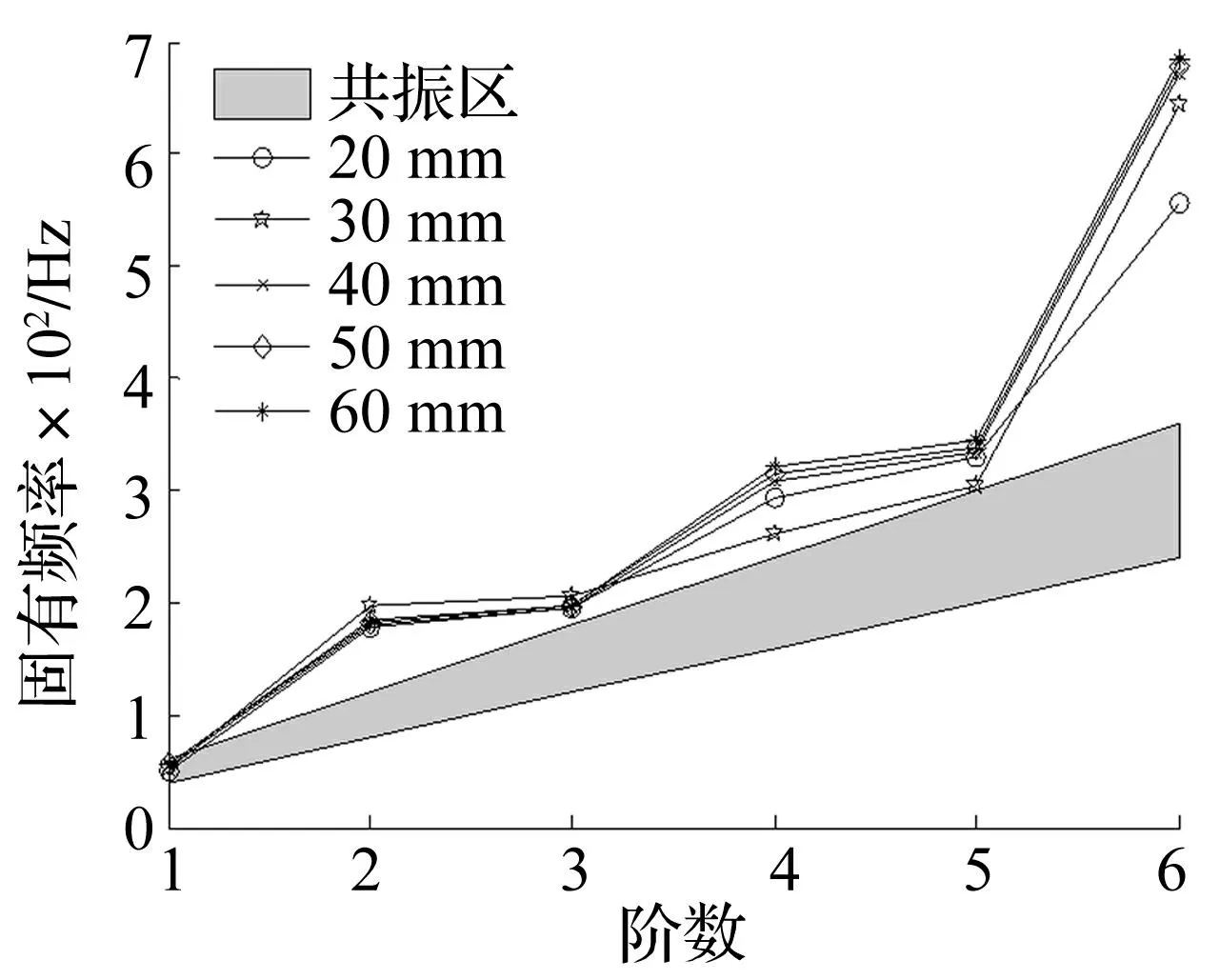
圖6　圓角半徑對管道固有頻率影響 Fig.6 Effect of round radius on pipe natural frequency

4.3固定支撐對管道固有頻率影響

落在共振區的管道一階固有頻率對應振型見圖7。由圖7可見，管道發生共振時拐彎處振動最強烈，振幅最大，故此處產生噪聲較大。增加固定支撐，改變原管道約束條件，增強剛度，其固有頻率會隨之增大，可有效避免管道產生共振，不會產生強烈噪聲。

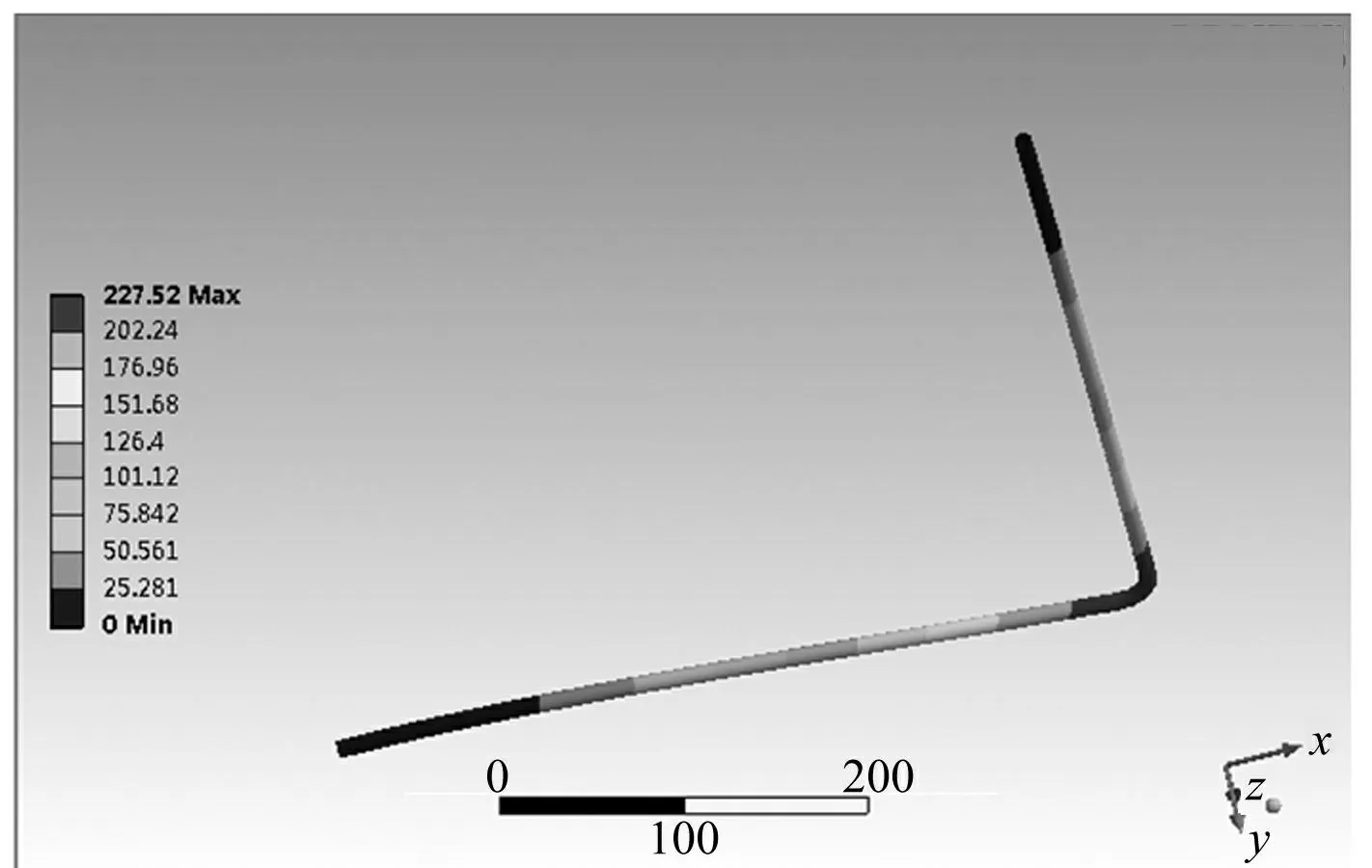
圖7　管道一階固有頻率對應振型 Fig.7 Vibration model at first natural frequency

分別在圖1的1～5點處即管道拐點及離拐點40 mm、60 mm、80 mm、100 mm五處增加固定支撐，計算結果見圖8。由圖8看出，增加固定支撐可使管道固有頻率大幅度增加，遠離共振區。值得注意的是，管道固有頻率并不隨固定支撐與拐點間距離增加呈線性變化。本文設定工況條件下，固定支撐與拐點間距離為60 mm時管道固有頻率增加最大，高于壓縮機激發頻率，制冷劑管道不會發生共振，亦能有效降低噪聲。

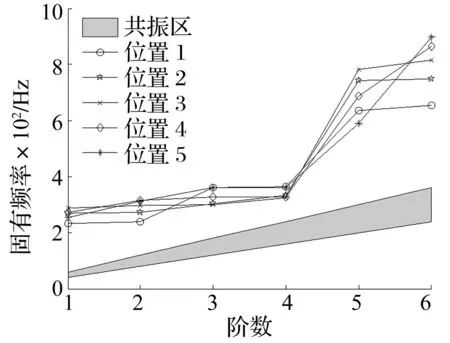
圖8　固定支撐對管道固有頻率影響 Fig.8 Effect of support location on pipe natural frequency

5結論

利用ANSYS模態分析模塊計算制冷劑管道內氣柱及管道固有頻率，分析長度、彎管圓角半徑及增加固定支撐對管道固有頻率影響，結論如下：

(1)氣柱固有頻率與壓縮機激發頻率相差較大，不會發生共振，即不會產生強烈噪聲。

(2)減小長度能使管道固有頻率遠離共振區，進而降低管道的振動、噪聲。

(3)增加彎管圓角半徑對管道固有頻率增幅較小，在激發源作用下仍會發生共振，產生較大噪聲。

(4)在合適位置增加固定支撐，可使管道固有頻率大幅度增加，能有效避免共振及降低噪聲。

參考文獻

[1]GB/T 19606-2004，家用和類似用途電器噪聲限值[S].

[2]Gue F, Cheong C, Kim T. Development of low-noise axial cooling fans in a household refrigerator[J]. Journal of Mechanical Science and Technology, 2011, 25(12): 2995-3004.

[3]Seo J Y, Kim W J, Won J S. Design and application of a perforated panel system to a household refrigerator for cooling fan noise reduction[J]. Journal of Mechanical Engineering Science, 2012, 226(3): 785-797.

[4]褚志剛,蔣忠翰,周亞男,等. 冰箱風扇質量在線檢測系統設計[J]. 振動與沖擊, 2012, 31(18): 96-99.

CHU Zhi-gang, JIANG Zhong-han, ZHOU Ya-nan, et al. Design of an online detection system for vibration quality of refrigerator fans[J]. Journal of Vibration and Shock, 2012, 31(18): 96-99.

[5]陳建良,金濤,孟曉宏,等. 冰箱壓縮機殼體噪聲輻射數值分析[J]. 浙江大學學報:工學版, 2007, 41(5): 794-798.

CHEN Jiang-liang, JIN Tao, MENG Xiao-hong,et al. Numerical analysis of noise radiation from refrigerator compressor shell[J]. Journal of Zhejiang University:Engineering Science, 2007, 41(5): 794-798.

[6]仲崇明,萬泉,蔣偉康. 往復式壓縮機振動的有限元數值分析與實驗研究[J]. 振動與沖擊, 2011, 30(5): 156-160.

ZHONG Chong-ming, WAN Quan, JIANG Wei-kang.Numerical analysis and tests for vibration response of a reciprocating compressor[J]. Journal of Vibration and Shock, 2011, 30(5): 156-160.

[7]郭維,劉斌,馮濤. 冰箱壓縮機機殼實驗模態分析[J]. 噪聲與振動控制, 2010 (3): 67-70.

GUO Wei, LIU Bin, FENG Tao. Experimentalmodal analysis of a refrigeration compressor’s shell[J]. Vibration and Noise Control, 2010(3): 67-70.

[8]趙科,金濤,童水光,等. 冰箱用動磁式直線壓縮機的動態特性仿真[J]. 浙江大學學報:工學版, 2009, 43(1): 138-142.

ZHAO Ke, JIN Tao, TONG Shui-guang,et al. Simulation of dynamic characteristics of moving magnet linear compressor for refrigerator[J]. Journal of Zhejiang University: Engineering Science, 2009, 43(1): 138-142.

[9]Kim H, Cho M G, Park J, et al. Prediction of gas pulsation of an industrial compressor[J]. Journal of Central South University, 2013, 20(10): 2735-2740.

[10]Lee S H, Ryu S M, Jeong W B. Vibration analysis of compressor piping system with fluid pulsation[J]. Journal of Mechanical Science and Technology, 2010, 26(12): 3903-3909.

[11]劉益才,曹立宏,楊智輝,等. 冰箱毛細管出口氣液兩相流理論[J]. 中南大學學報:自然科學版, 2007, 38(3): 450-453.

LIU Yi-cai, CAO Li-hong, YANG Zhi-hui,et al. Theoretical research on gas-liquid two-phase flow at outlet of refrigerator capillary[J]. Journal of Central South University: Science and Technology, 2007, 38(3): 450-453.

[12]Han H S, Jeong W B, Kim M S, et al. Reduction of the refrigerant-induced noise from the evaporator-inlet pipe in a refrigerator[J]. International Journal of Refrigerator, 2010, 33(7): 1478-1488.

[13]李春銀,王樹林. 汽車空調旋葉式壓縮機排氣閥片的振動特性[J]. 振動與沖擊, 2014, 33(8): 186-191.

LI Chun-yin, WANG Shu-lin.Vibration behavior of a discharge valve for vane compressor of a car air conditioner[J]. Journal of Vibration and Shock, 2014, 33(8): 186-191.

[14]徐斌,馮全科,余小玲. 壓縮機復雜管路壓力脈動即管道振動研究[J]. 核動力工程, 2008, 29(4): 79-83.

XU Bin, FENG Quan-ke, YU Xiao-ling.Study on pressure pulsation and piping vibration of complex piping of reciprocating compressor[J]. Nuclear Power Engineering, 2008, 29(4): 79-83.

[15]楊國安. 機械振動基礎[M]. 北京:中國石化出版社, 2012.

[16]盛美萍,王敏慶,孫進才. 噪聲與振動控制技術基礎[M].北京:科學出版社, 2007.

[17]舒歌群,高文志,劉月輝. 動力機械振動與噪聲[M]. 天津:天津大學出版社, 2008.