考慮地形條件影響的車橋耦合系統地震響應分析

第一作者喬宏女，博士生，1989年9月生

通信作者夏禾男，教授，1951年4月生

考慮地形條件影響的車橋耦合系統地震響應分析

喬宏,夏禾,杜憲亭,南勇

(北京交通大學土木建筑工程學院，北京100044)

摘要：研究局部地形條件對地震作用下車橋耦合系統動力響應的影響。依據黏彈性邊界理論，利用ANSYS建立了可以考慮局部地形條件的三維場地模型，并通過將輸入地震動轉化為作用于人工邊界上的等效荷載來實現波動輸入，得到考慮地形影響之后的橋梁各支點地震動時程曲線。將地震激勵以速度時程和位移時程形式作用到結構上，編制計算程序，進行多點地震激勵作用下的車橋耦合分析。以列車通過總長480 m的實際橋梁為算例，對考慮局部地形影響的車橋耦合系統地震響應進行了仿真分析。結果表明：考慮地形影響后，地震作用下橋梁和車輛的動力響應在峰值大小和峰值出現時間上均發生了改變，且其變化規律隨橋梁所處的地形類型的不同而有所差別，說明進行車橋耦合系統地震響應分析時考慮局部地形影響的必要性。

關鍵詞：車橋耦合系統；動力分析；地震作用；地形效應；黏彈性人工邊界

基金項目：國家973計劃項目(2013CB036203);國家自然科學基金項目(51208027);中央高校基本科研業務費專項資金資助 (2014YJS095)

收稿日期：2014-11-21修改稿收到日期：2015-01-20

中圖分類號:U441

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.17.012

Abstract:The influences of topography on the dynamic response of a train-bridge system under earthquake were studied. According to the theory of visco-elastic artificial boundary, a 3-D finite element site model accounting for topographic effects was established by using ANSYS. The process of wave input was realized by converting the seismic time history into equivalent loads acting on the artificial boundary, the seismic time history curve at each support of the bridge was obtained. The dynamic analysis of the train-bridge coupled system subjected to multi-support seismic excitations was performed, the velocity and displacement time histories of seismic excitations were exerted on the bridge supports. With a train passing through a 480m-bridge as a case study, the dynamic responses of the train-bridge coupled system under earthquakes considering local topography were simulated. The results showed that the peak value and the time of peak appearance for the dynamic response of the train-bridge system vary and the variation laws are different due to different topographic effects, so it is necessary to consider topographic effects in dynamic analysis of train-bridge coupled systems under earthquakes.

Seismic response analysis of a train-bridge coupled system considering topographic effects

QIAOHong,XIAHe,DUXian-ting,NANYong(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Key words:train-bridge coupled system; dynamic analysis; earthquake action; topographic effects; visco-elastic artificial boundary

近些年來，隨著鐵路事業的飛速發展，我國的鐵路橋梁數量與日俱增，在地震易發區列車在橋上行駛時遭遇突發地震的可能性大大提高。地震作用下車橋耦合問題已經成為當前研究的熱點之一[1-4]。在地形條件復雜的山區，實際地震中存在的地形對地震作用的放大現象引起了人們的注意。Celebi通過對1985年智利地震(Central Chile，M7.8)余震的地震實測數據進行觀察發現，山脊頂及陡崖受到的地震破壞作用相對較大[5]。在該次地震中，沿兩個山脊和緊鄰一個山脊的山谷中，由同一承包商建設的鋼混框架結構公寓的震害截然不同，建在山脊上的公寓破壞嚴重，而建在山谷場地中的公寓沒有遭到破壞[6]。Jibson實測了五次地震下日本一座山脈各點的加速度峰值，發現相較于山腳，山頂處的加速度峰值放大了1.8～5.5倍。我國汶川地震中廟子坪大橋、百花大橋的破壞除了地震烈度高的原因外，所處的復雜地形或許也是其中因素之一[8]。因此，局部地形條件對車橋耦合系統地震響應的影響值得關注。

到目前為止，國內外的相關研究主要集中于局部場地條件對橋梁地震響應的影響分析[9-11]，極少考慮地形條件對車橋耦合系統地震響應的影響。

本文基于黏彈性人工邊界理論和有限元方法，建立了能夠反映橋梁局部場地條件的三維分析模型，將輸入地震動轉化為作用于人工邊界上的等效荷載來實現波動輸入，得到結構支撐處地震動時程。將考慮地形影響之后的橋梁支撐處地震動作為外激勵施加到車橋耦合振動系統上，以某實際工程為例，編制相關計算程序，研究了地形條件對地震作用下車橋系統動力響應的影響規律。

1考慮地形條件影響的地震動

采用有限元軟件實現地震動輸入問題時，一般是從無限介質中切取出有限尺寸的計算區域，通過在有限區域的邊界上引入適當的人工邊界條件來實現無限區域的模擬。建立人工邊界條件的關鍵在于所建立的邊界上不存在能量反射。Liu等[12]提出的三維黏彈性人工邊界除滿足以上條件外，還具有計算精度高、計算穩定性好，應用方便等優點，因此本文在建立場地模型時，選擇了黏彈性人工邊界。

1.1外源輸入的等效邊界力法

文獻[13]中將輸入地震動轉化為作用于人工邊界上的等效荷載的方法來實現波動輸入，其人工邊界的法向和切向等效荷載分別為：

KBNu0(xB,yB,t)

(1)

KBTv0(xB,yB,t)

(2)

式中:u0(x,y,t)和v0(x,y,t)分別為入射波的法向和切向位移；σ0(x,y,t)和τ0(x,y,t)分別為法向應力和切向應力；xB和yB是人工邊界節點坐標，KBN、KBT、CBN、CBT分別為黏彈性人工邊界的法向、切向彈簧系數和阻尼系數[12]。

1.2等效地震力計算

地震時一般震源較深，且地震波向上傳播過程中要經過各種不同巖層的折射，導致地震波到達地表時已接近垂直入射。因此，本文假設地震波以平面波形式自底邊界豎直入射，且豎直入射的平面P波和S波的位移時程分別為uP(t)和uS(t)。直角坐標系的x-y面平行于底邊，z方向指向有限域，見圖1。

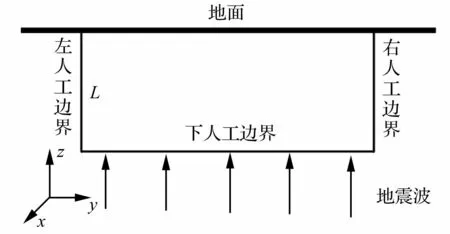
圖1　地震波豎直入射模型 Fig.1 Vertical incidence model of seismic wave

假設S波沿x軸方向振動，則由波動傳播規律及波場應力狀態可以解析得到各人工邊界節點的等效地震荷載[14-15]，即：

(1)P波入射

(3)

(4)

(5)

(6)

(7)

(2)S波入射

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

式中:各節點等效地震荷載的下標代表應力方向;上標代表節點所在邊界的外法線方向；Δt1～Δt4分別代表入射P波、地表反射P波、入射S波及地表反射S波的時間延遲；l為節點到底邊界的距離；L為底邊界到地表的距離；A為邊界節點的人工邊界影響面積，具體取值參考文獻[12]，λ、ρ、cp、cs分別為介質的一階拉梅常數、密度、縱波波速和橫波波速。

1.3黏彈性人工邊界的實現

以ANSYS軟件為例，場地介質可以利用Solid45單元模擬，黏彈性人工邊界的彈簧和阻尼器可以通過在每一個邊界節點添加一端固定的Combin14單元模擬。

2地震荷載作用下車橋系統動力分析模型

如圖2所示為車橋耦合系統的示意圖，它由橋梁子系統和車輛子系統所組成。假定列車沿橋梁縱向勻速行駛，且橋梁各支撐處地震地面運動不一致。車橋系統絕對坐標系滿足右手準則，其中，y方向為橋梁縱向，x方向為橋梁橫向，z方向為豎直方向，為方便計算，在這里取向下為正方向。假設地震只對橋梁子系統產生直接影響，對于車輛子系統的影響，則通過基礎、橋墩、橋面、軌道傳遞給車輛子系統，即地震對車輛子系統的影響可以通過輪軌關系實現，無需在車橋耦合動力分析模型中特別考慮地震對車輛子系統的影響。

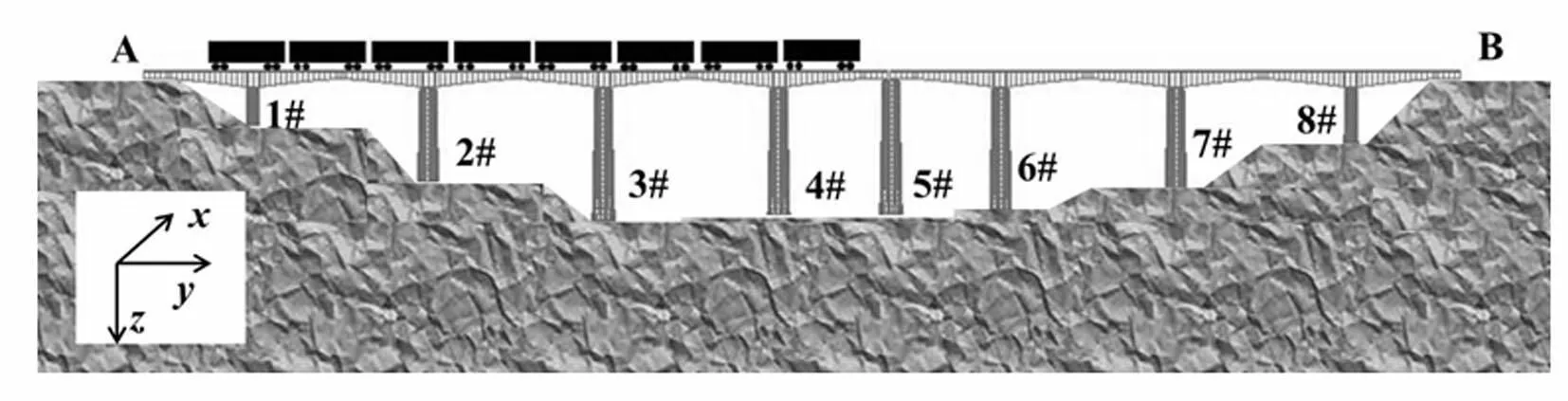
圖2　車橋耦合系統 Fig.2 The bridge-train system

如果采用有限元法描述地震作用下的車橋耦合振動，則在絕對坐標系下，車輛、橋梁子系統的動力平衡方程分別為[2]：

(16)

(17)

將式(17)中的第一項展開，可以得到有限元法描述下的橋梁結構自身各點的運動平衡方程，即：

(18)

由于Msb常被忽略，因此，式(18)變為：

(19)

其中等號右邊的前兩項即為地震作用到橋梁結構上的荷載。

將式(19)利用振型分解法進行模態降階，可以得到：

(20)

式中:φi和qi為質量歸一化的第i階振型和廣義坐標；ωi和ξi分別為第i階頻率和阻尼比；n為分析中所用到的橋梁模態數；R為影響矩陣，R=-K-1ssKsb。

式(16)和式(20)構成了地震作用下車橋耦合系統動力平衡方程組，通過編制相應的計算程序，迭代求解這兩式即可得到地震作用下車橋耦合系統的動力響應。

3算例

為研究地形條件對車橋耦合系統地震響應的影響，選取某實際橋梁作為算例進行分析。

橋梁全長為480 m，由兩聯連續梁跨組成，跨度布置為(40+64+64+64+40) m+(40+64+64+40) m。橋梁梁體采用單箱單室變高度直腹板箱型截面，主墩墩頂5 m范圍內梁高相等，為6.05 m，見圖3(a)；跨中及邊墩墩頂現澆段梁高3.05 m，梁體截面見圖3(b)。梁底曲線為二次拋物線。

橋墩為圓端形空心墩，墩頂3 m范圍，墩底3m范圍為實體段。橋墩高度分別為13.5 m、34 m、48.5 m、46 m、49 m、45.5 m、36 m和20 m。橋梁所處的地形條件見圖2。沿著橋梁縱向，將橋梁橋墩分別編號為1#，2#……8#，兩個橋臺分別命名為A橋臺和B橋臺。

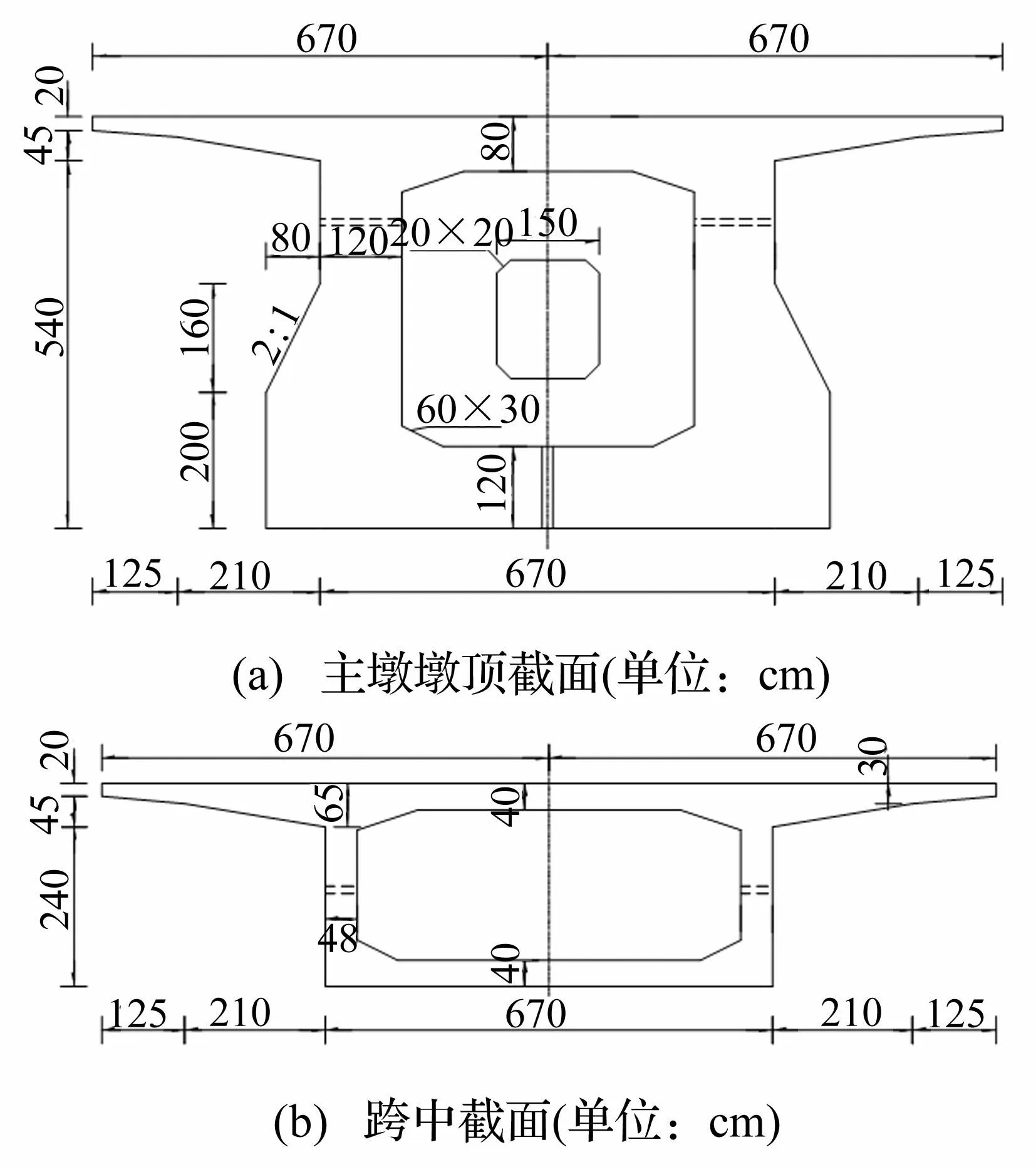
圖3　橋梁截面示意圖 Fig.3 Sections of the bridge

橋梁有限元模型采用梁單元建立，邊界條件取為墩底全部固結，梁體和橋墩之間設置主從節點。其中，在兩聯連續梁連接處，兩聯梁體分別設置從屬節點，均從屬于共用橋墩上的主節點。建立的有限元模型見圖4(a)。取橋梁的前100階模態進行車橋耦合分析，編制計算程序，在計算過程中橋梁各階模態的阻尼比均假定為0.05。

對所建橋梁有限元模型進行模態分析，可以得到該橋梁的自振頻率和振型，其中前8階的自振頻率及模態振型見圖4(b)。

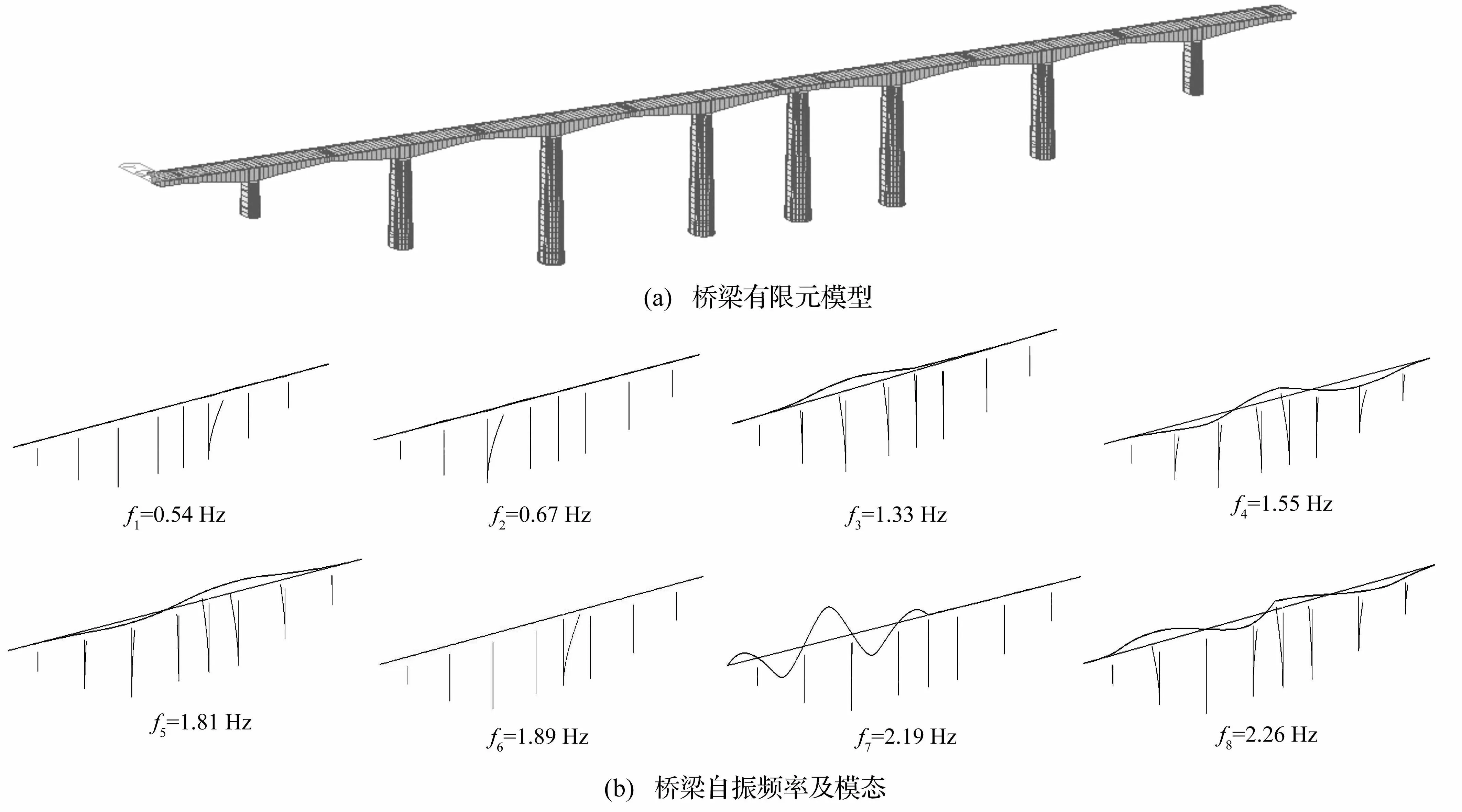
圖4　橋梁有限元模型及各階自振特性 Fig.4 FE model and mode parameters of the bridge

分別假設該橋位于河谷處和兩山峰之間，建立ANSYS場地模型，分析地形條件對車橋耦合系統地震響應的影響。

橋梁所在場地有限元模型采用Solid45單元模擬，單元尺寸設為8，土層密度ρ=2 610 kg/m3，彈性模量為E=5 GPa，泊松比為0.26，阻尼比為0.05，P波的傳播速度為cp=1 530 m/s。如前文所述利用Combin14單元建立黏彈性邊界，最終建立場地有限元模型見圖5，其中，河谷地形和山峰地形的有限元模型尺寸分別為640 m×160 m×160 m和1 760 m×160 m×260 m。

地震波選取某實際地震中記錄的地震加速度時程，將其進行積分并消除基線偏移，得到該地震的速度時程和位移時程曲線，見圖6。分別假設該波為平面P波和平面S波，根據式(3)～(7)及式(8)～(14)求得各節點需輸入的節點等效荷載，得到考慮地形條件影響的橋梁各支點豎向和橫向地震動時程。將地震激勵以速度時程和位移時程形式作用到結構上，進行多點激勵作用下地震-車-橋耦合分析，研究地震作用下車橋耦合系統的豎向和橫向動力響應。

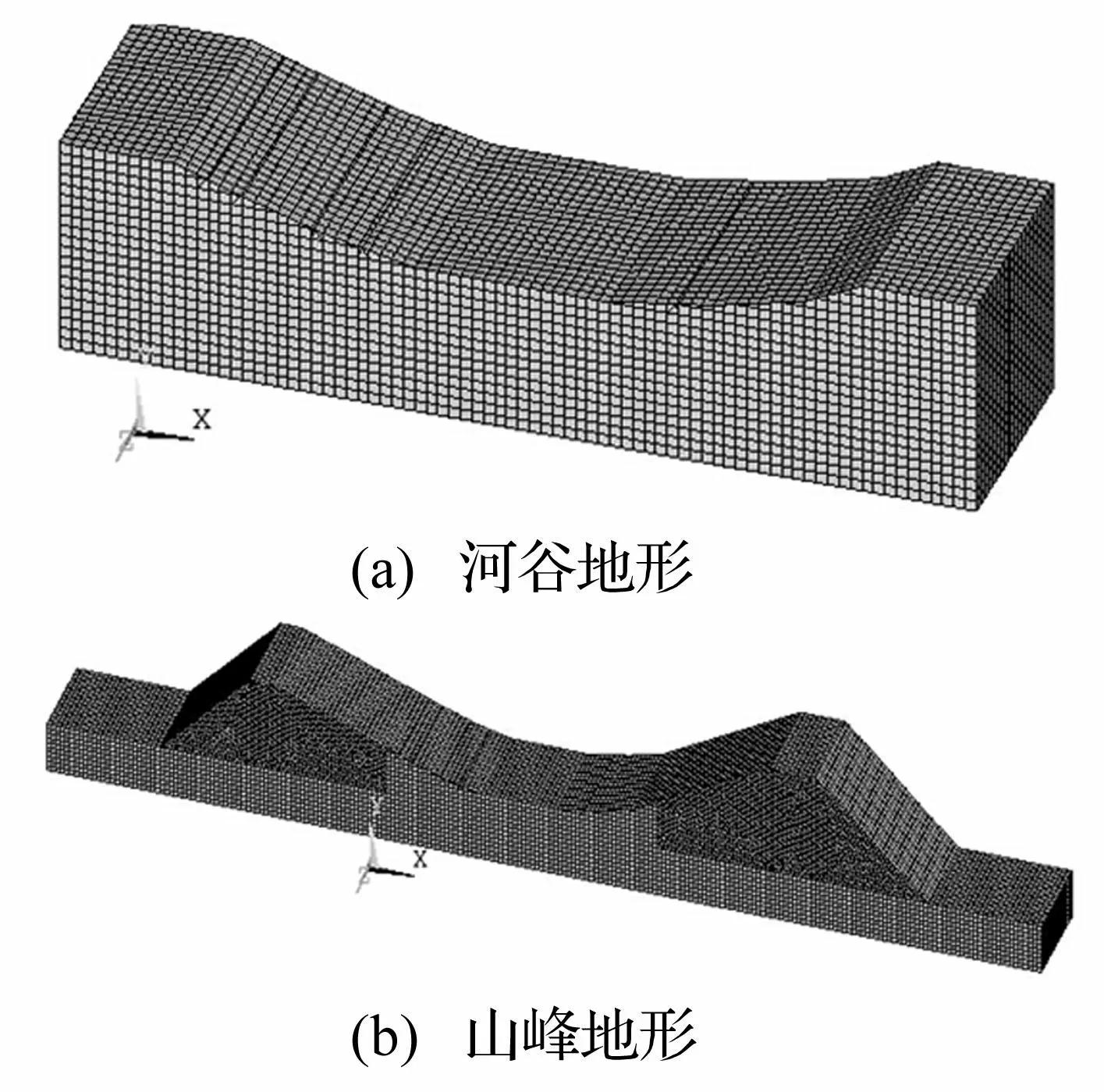
圖5　場地有限元模型 Fig.5 Finite element model of local topography

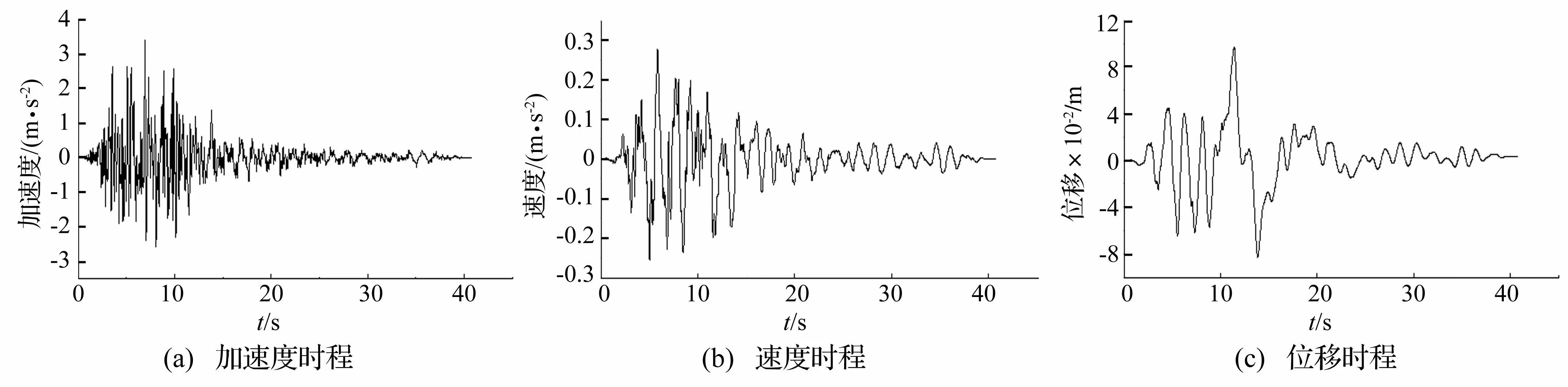
圖6　地震動時程 Fig.6 Seismic time history

車輛模型選擇ICE3高速列車，共有8節，并采用3動1拖的編組設置。每節車采用剛體-彈簧-阻尼離散模型，車體之間視為相互獨立的單元，采用達朗貝爾原理推導其質量矩陣、阻尼矩陣和剛度矩陣，形成運動方程[16]。分析車速為150 km/h。輪軌接觸關系采用密貼假定，軌道不平順采用德國低干擾譜，其高低不平順見圖7。

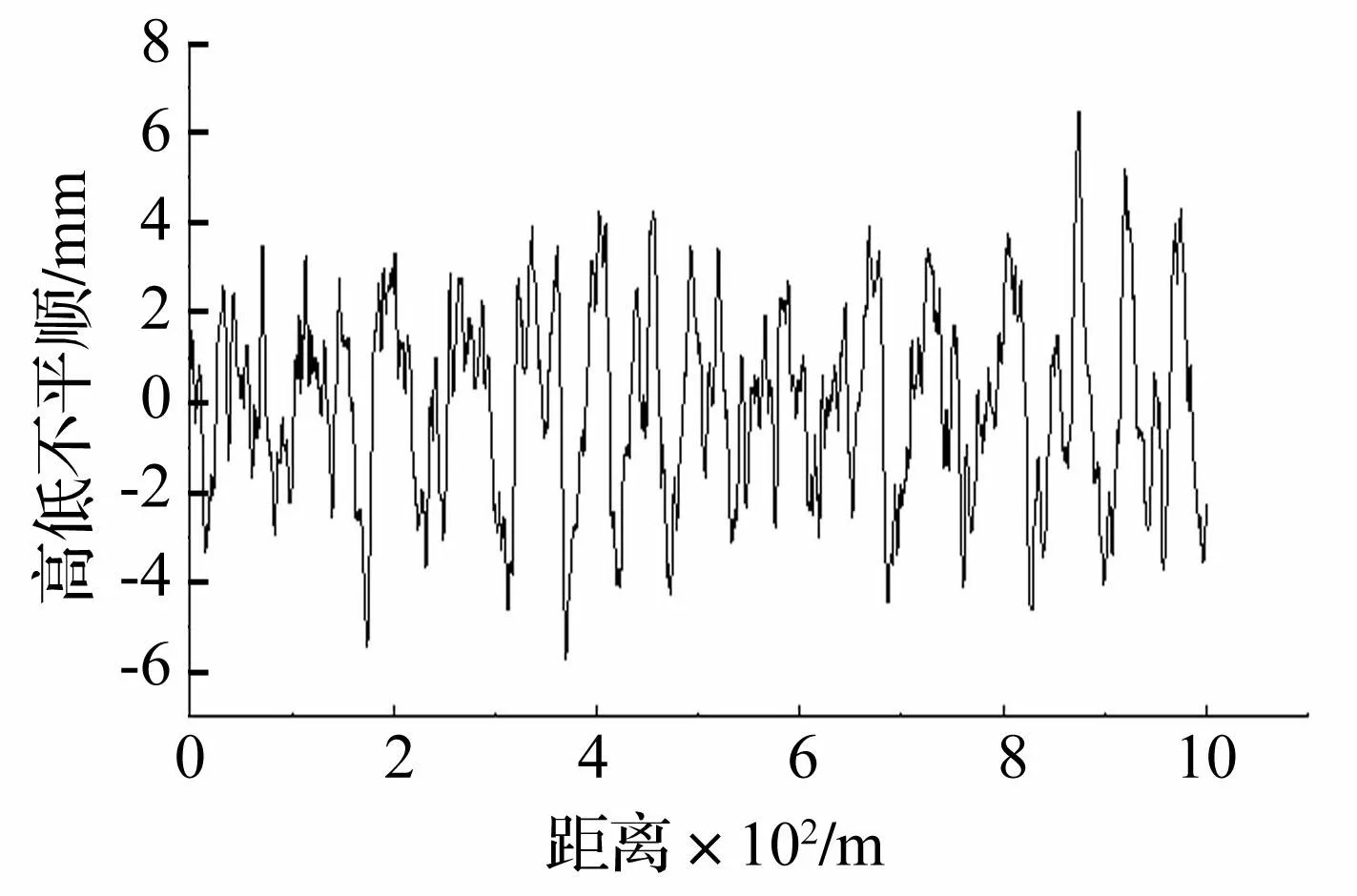
圖7　軌道高低不平順 Fig.7 Vertical track irregularity curve

假設列車上橋時剛好發生地震。依據以上條件編制地震多點激勵作用下車橋耦合計算程序，進行考慮地形條件影響的車橋耦合系統地震響應分析。

3.1橋梁各支點地震動時程

計算中，分別采用考慮與不考慮地形影響的兩種場地模型。在不考慮地形效應影響的模型中把模型的上表面取為自由水平表面[11]，建立有限元模型，獲取橋梁各支點的地震動時程。

如表1所示為橋梁各支點處考慮地形效應影響后的地震動位移時程最大值與不考慮地形效應時地震動位移時程最大值的比值。其中，橫向位移最大值按+x和-x方向分別考慮，而豎向位移最大值按+z和-z兩個方向分別考慮，見圖2。從表中可以看出，對于橫向位移，考慮地形效應影響后，河谷地形中各支點橫向位移最大值在兩個方向上均減小；而山峰地形中，+x方向各支點橫向位移最大值增大，-x方向各支點橫向位移最大值減小；對于豎向位移，河谷地形中各支點兩個方向上豎向位移最大值均減小，而山峰地形中各支點兩個方向上豎向位移最大值均增大。

表1　橋梁各支點地震動位移時程最大值比值

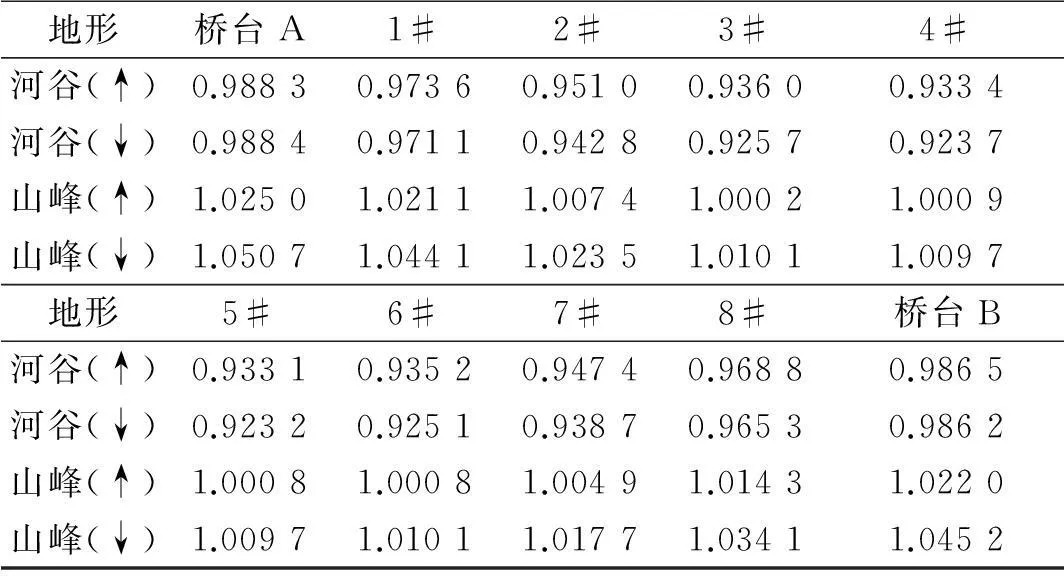
(b)豎向

3.2河谷地形下P波入射條件下動力分析結果

圖8、圖9分別給出了河谷地形中車速150 km/h條件下P波入射時第1座連續梁第3跨跨中節點和第一節車車體在地震作用下的豎向加速度時程。

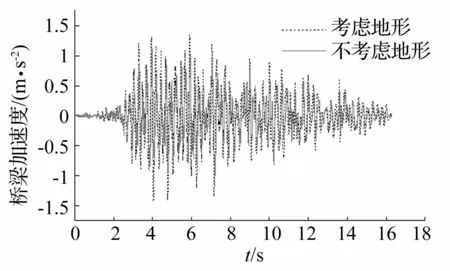
圖8　橋梁豎向加速度時程 Fig.8 Vertical acceleration time history of bridge

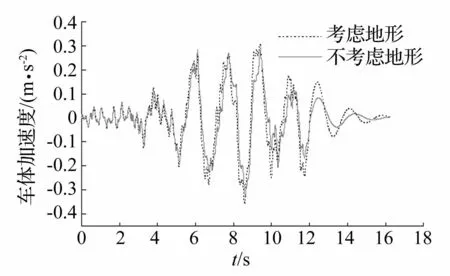
圖9　車體豎向加速度時程 Fig.9 Vertical acceleration time history of 1 st car-body

從圖中可以看出，考慮地形影響后，河谷地形地震P波作用下，車橋耦合系統中橋梁子系統動力響應變大，考慮地形影響后的橋梁加速度最大值為不考慮時最大值的1.25倍左右；而車輛子系統的動力響應亦有所放大，考慮地形影響之后車體豎向加速度最大值約為不考慮時最大值的1.08倍，且峰值發生的時刻也發生了改變。

3.3河谷地形下S波入射條件下動力分析結果

如圖10、圖11分別為河谷地形中車速為150 km/h條件下S波入射時第1座連續梁第3跨跨中節點和第一節車車體在地震作用下的橫向加速度時程。

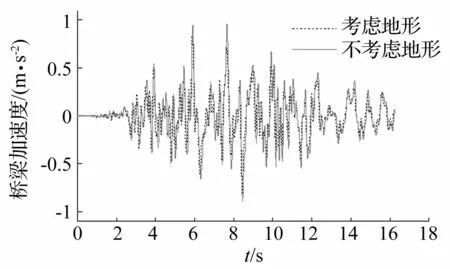
圖10　橋梁橫向加速度時程 Fig.10 Lateral acceleration time history of bridge

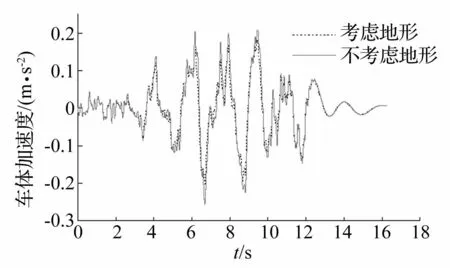
圖11　車體橫向加速度時程 Fig.11 Lateral acceleration time history of 1 st car-body

從圖中可以看出，考慮地形條件影響后，地震S波作用下橋梁和車輛子系統的動力響應均變小，橋梁和車體橫向加速度最大值分別為不考慮地形時各自最大值的0.92倍和0.80倍。從表1中可以看出，這與考慮地形條件影響后橋梁各支點橫向地震動峰值較不考慮時減小有關。說明了河谷地形對地震作用下車橋耦合系統橫向動力響應具有一定的有利作用。

3.4山峰地形下P波入射條件下動力分析結果

圖12、圖13分別給出了山峰地形中車速150 km/h條件下P波入射時第1座連續梁第3跨跨中節點和第一節車車體在地震作用下的豎向加速度時程。

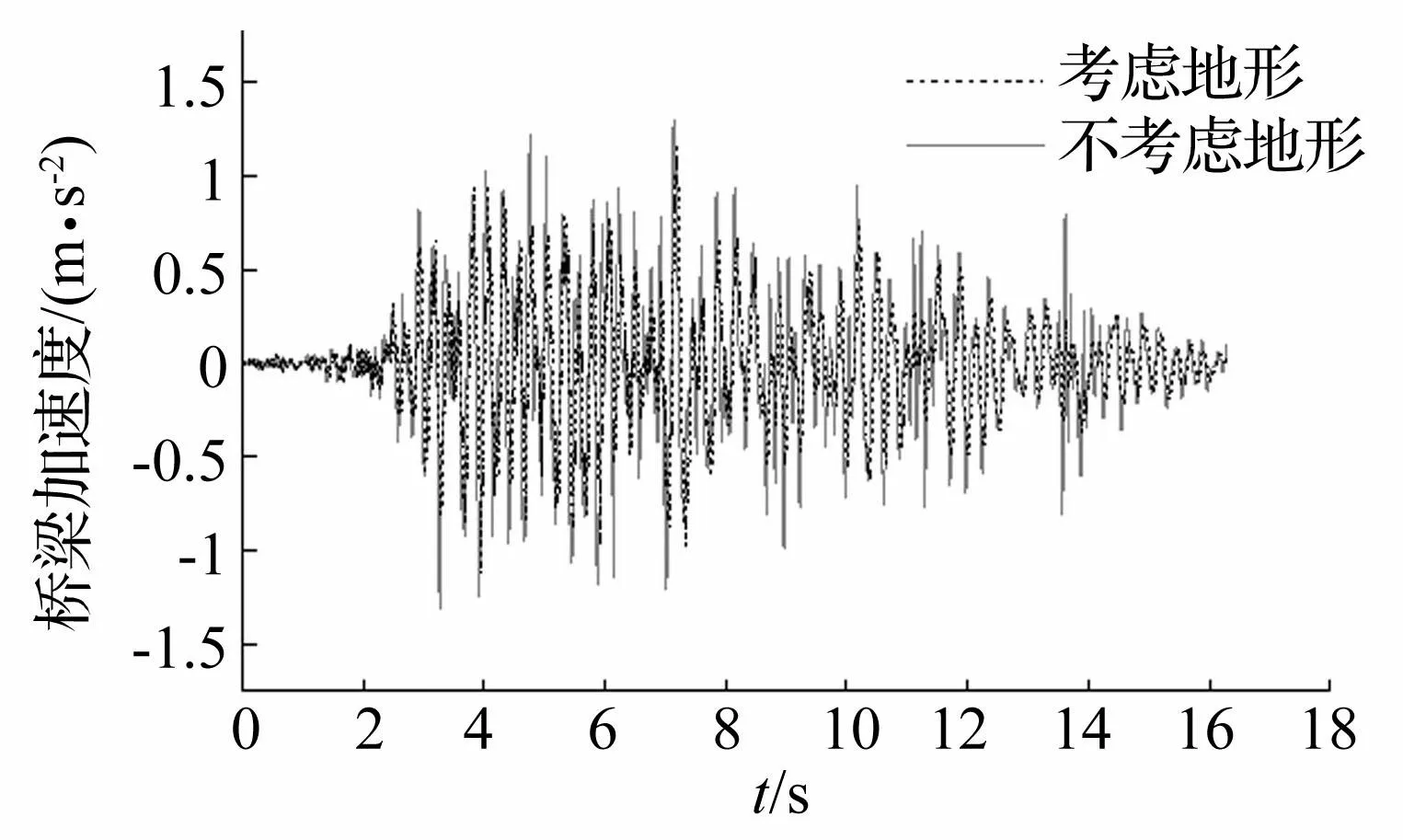
圖12　橋梁豎向加速度時程 Fig.12 Vertical displacement time history of bridge

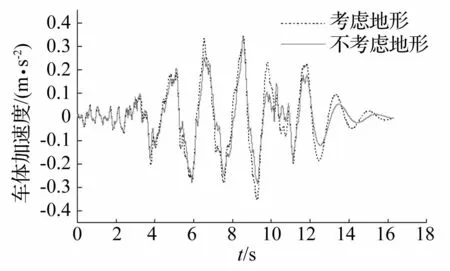
圖13　車體豎向加速度時程 Fig.13 Vertical acceleration time history of 1 st car body

從圖中可以看出，考慮地形影響后，山峰地形地震P波作用下車橋耦合系統中橋梁子系統的動力響應變小，考慮地形影響后的橋梁加速度最大值為不考慮時的0.90倍左右；而車輛子系統的動力響應有所放大，考慮地形影響之后車體豎向加速度最大值約為不考慮時最大值的1.03倍，且峰值發生的時刻也發生了改變。

3.5山峰地形下S波入射條件下動力分析結果

如圖14、圖15分別為山峰地形中車速為150 km/h條件下S波入射時第1座連續梁第3跨跨中節點和第一節車車體在地震作用下的橫向加速度時程。

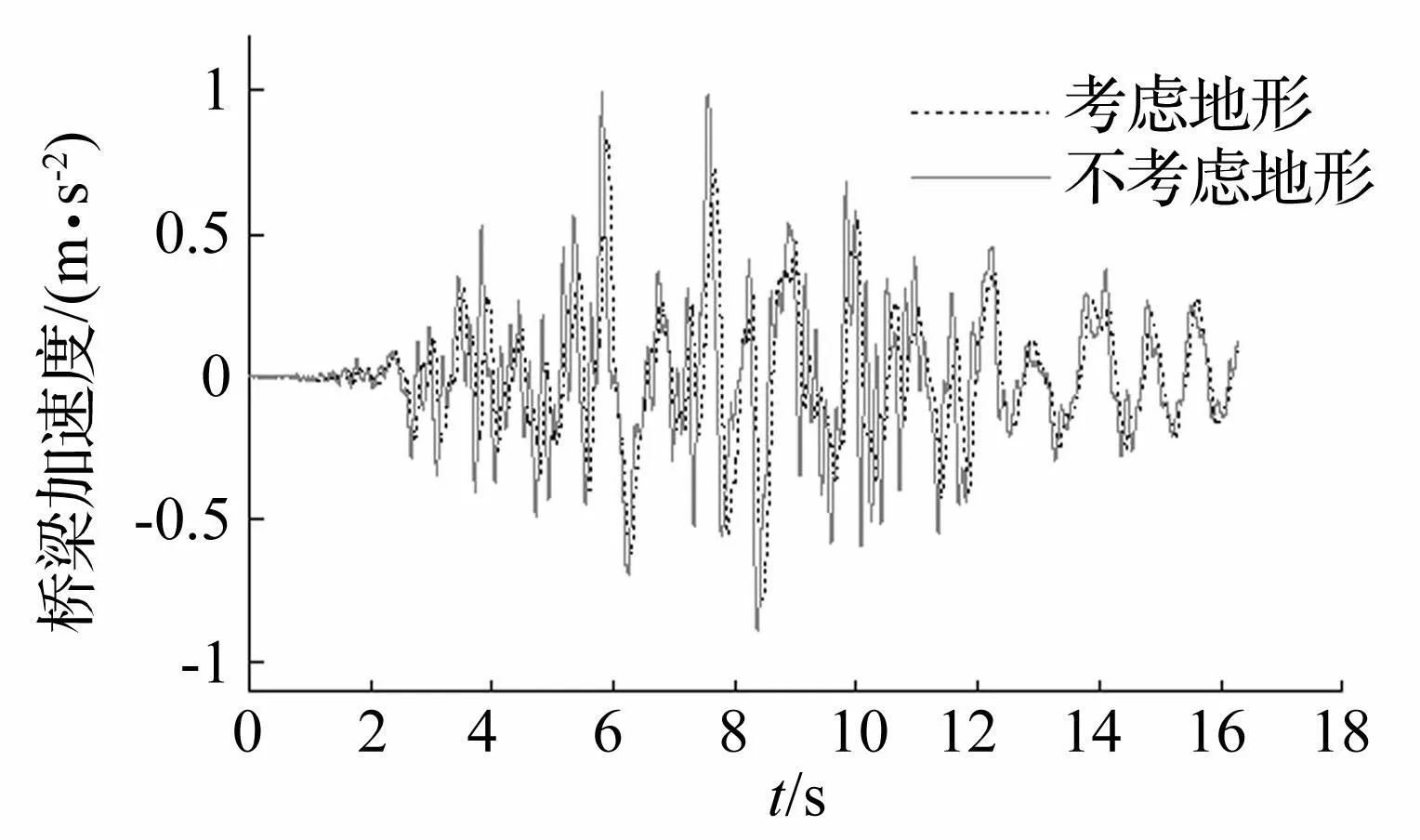
圖14　橋梁橫向加速度時程 Fig.14 Lateral displacement time history of bridge

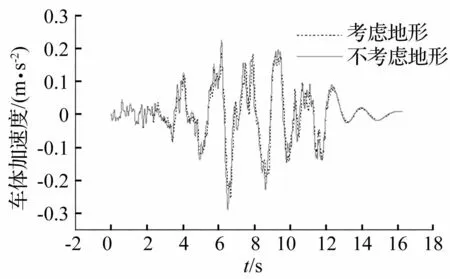
圖15 車體橫向加速度時程 Fig.15 Lateral acceleration time history of 1 st car body

從圖中可以看出，考慮地形條件影響后，山峰地形地震S波作用下橋梁的橫向加速度和車體的橫向加速度均有所減小，分別為不考慮地形影響時的0.83倍和0.88倍。這可能與考慮地形效應影響后，各支點在+x和-x兩個方向上變化趨勢不一致有關。另外，從圖中可以發現，車橋系統地震響應峰值出現的時間也有一定延遲，說明局部地形既改變了車橋耦合系統地震響應的峰值大小，又改變了其峰值出現的時刻。

通過對以上算例進行初步分析，可以發現：S波入射情況下，不管是河谷地形還是山峰地形，橋梁動力響應和車輛動力響應均變小；P波入射情況下，地形條件對地震作用下車橋耦合系統動力響應的影響隨著地形類型的不同而變化，河谷地形條件下，車橋耦合系統地震響應較不考慮地形條件時增大，而山峰地形條件下，橋梁地震響應減小而車體振動響應增大。

為進一步研究P波和S波入射情況下山峰地形和河谷地形對車橋耦合系統地震響應的影響，圖15、16和圖17、18分別給出了不同車速時，P波和S波入射情況下考慮地形影響的橋梁第1座連續梁第3跨跨中節點的豎向加速度最大值和第一節車車體豎向加速度最大值與不考慮地形影響時各自最大值的比值，簡稱比值。其中，車速在150 km/h ～300 km/h之間變化，每30 km/h為一個等級。

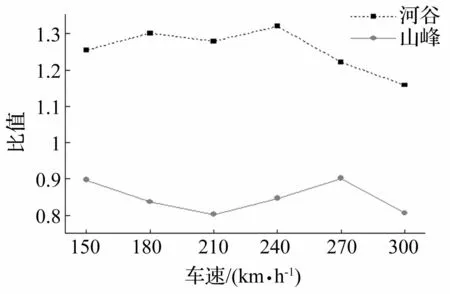
圖16　P波入射時各車速下橋梁豎向加速度比值 Fig.16 Ratios of bridge vertical acceleration under different train speeds subjected to incident P wave

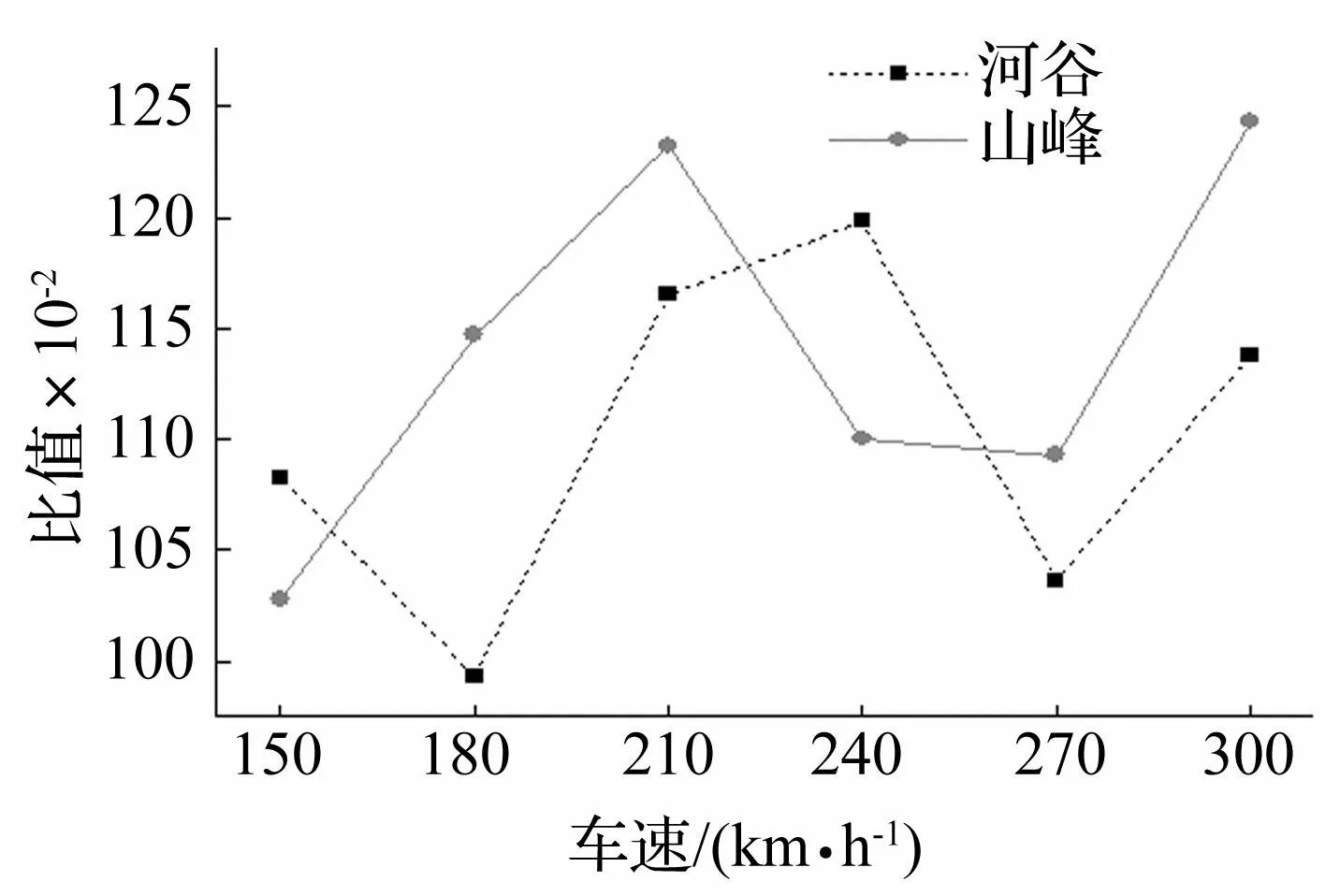
圖17　P波入射時各車速下車體豎向加速度比值 Fig.17 Ratios of vehicle vertical acceleration under different train speeds subjected to incident P wave

從圖16和圖17中可以看出，各車速時，山峰地形下橋梁豎向加速度比值均小于1，河谷地形下橋梁豎向加速度比值均大于1，說明河谷條件對橋梁豎向振動具有放大作用而山峰地形條件對橋梁豎向振動具有減小作用；而車體豎向加速度比值則不具有以上規律，這與計算時加入了軌道不平順有關。從圖18和圖19中可以看出，兩種地形條件下，橋梁橫向加速度在各車速時最大值均減小，但是河谷地形條件下的比值均大于山峰地形條件下的比值，說明相較于河谷地形，山峰地形對橋梁橫向振動響應的影響更加明顯。

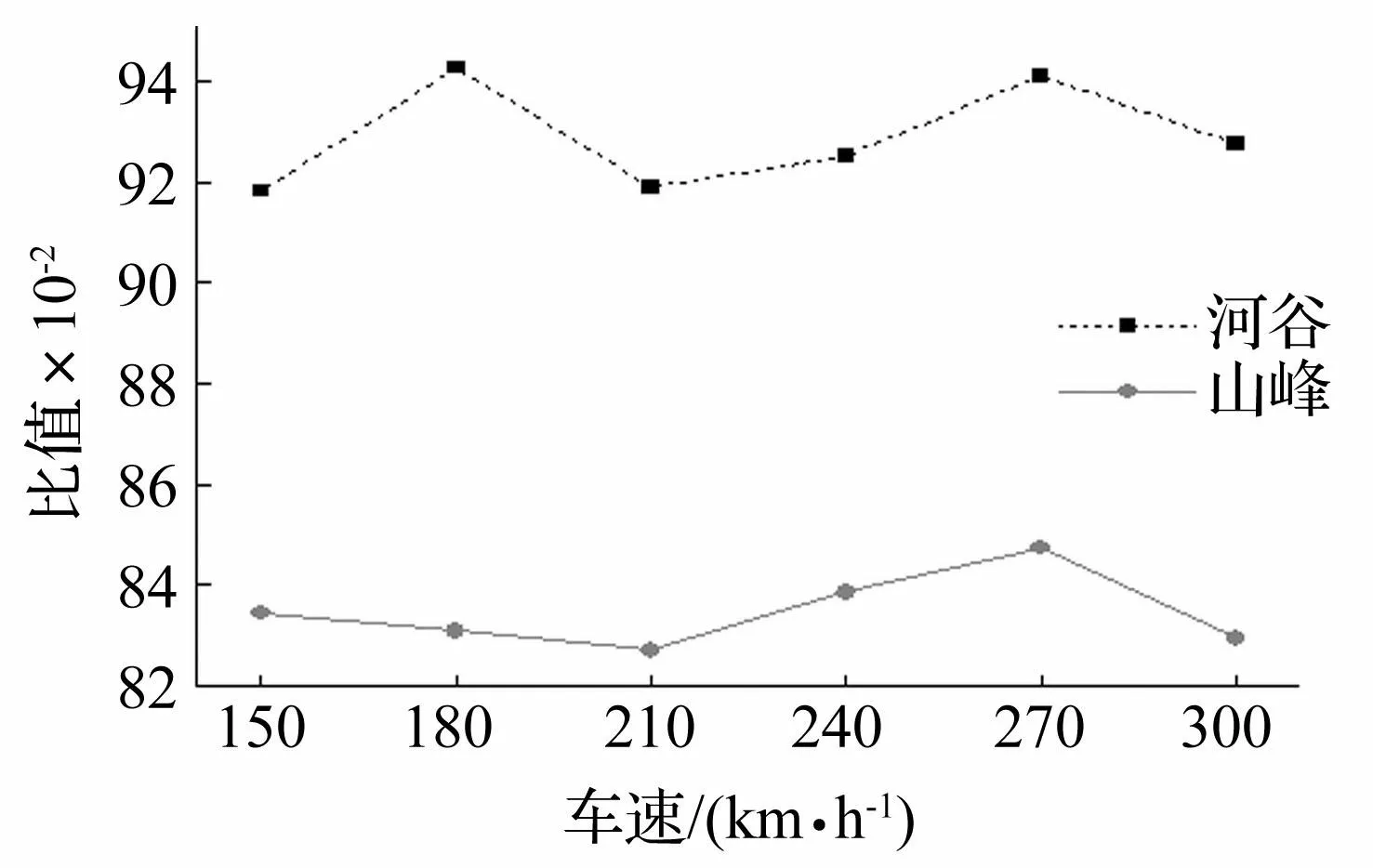
圖18　S波入射時各車速下橋梁橫向加速度比值 Fig.18 Ratios of bridge lateral acceleration under different train speeds subjected to incident S wave

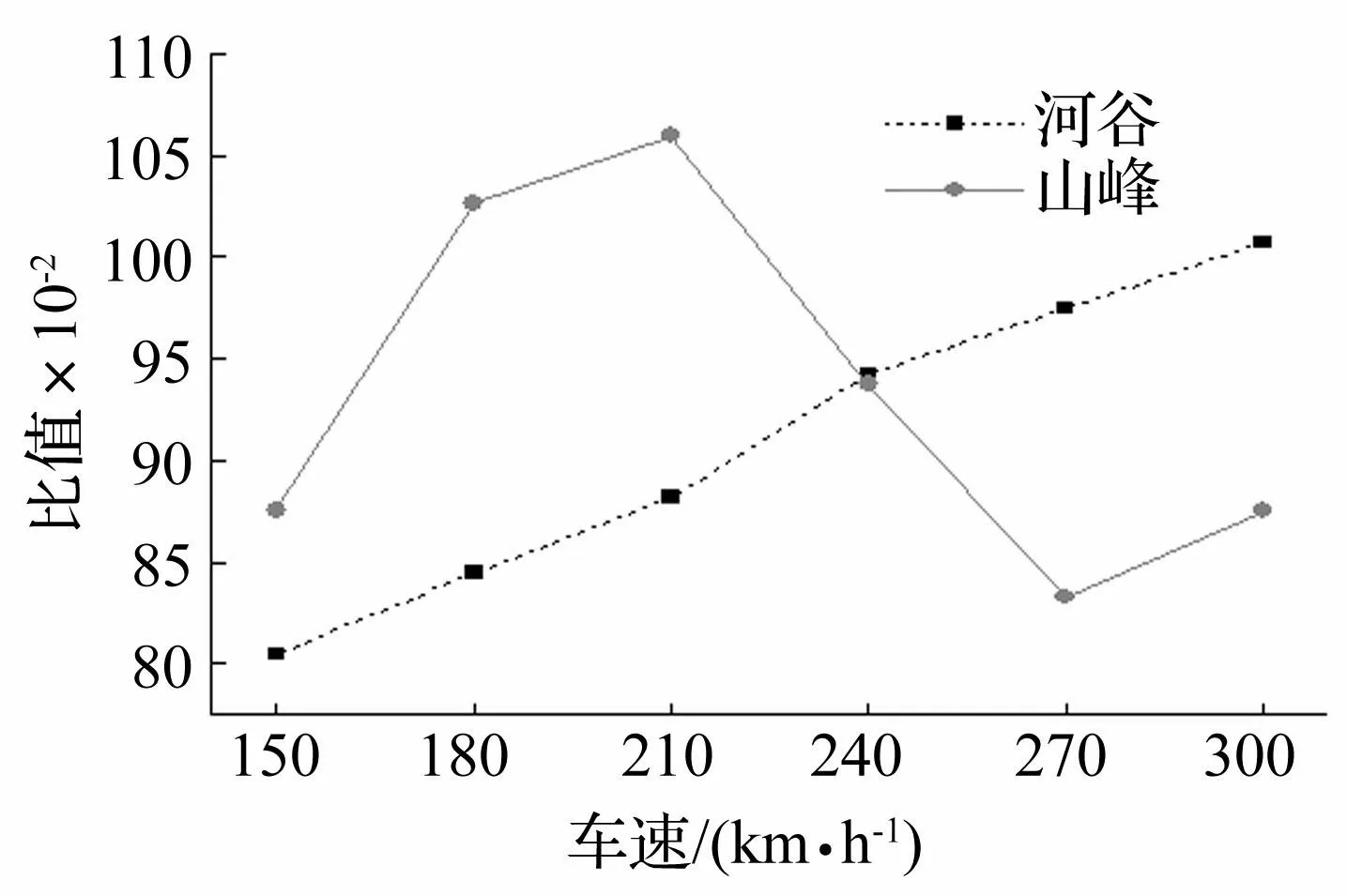
圖19　S波入射時各車速下車體橫向加速度比值 Fig.19 Ratios of vehicle lateral acceleration under different train speeds subjected to incident S wave

4結論

本文建立了能夠反映橋梁局部場地條件的三維分析模型，編制程序計算了考慮地形影響的車橋耦合系統地震響應，并通過算例進行了初步探討。根據計算結果，可以得到如下結論：

(1)考慮地形條件影響后，地震作用下車橋耦合系統的動力響應的峰值及其出現時間發生了變化。

(2)P波入射情況下，不管是河谷地形還是山峰地形，車輛豎向動力響應均變大，而橋梁豎向動力響應在河谷地形條件時變大，在山峰地形條件時變小。因此，在橋梁抗震設計時，應考慮地形條件的影響以保證計算結果偏于安全。

(3)S波入射情況下，不管是河谷地形還是山峰地形，橋梁和車輛的橫向動力響應均變小，但產生該結果的原因不同：河谷地形條件下，車橋耦合系統地震響應減小的原因為考慮地形條件影響后，地震動輸入峰值減小；山峰地形條件下，地震動輸入峰值在兩個方向上變化趨勢不同，從而導致了加入軌道不平順后的車橋耦合系統地震響應減小，關于這種現象產生的原因，將在以后進行深入探討。

參考文獻

[1]Xia H, Han Y, Zhang N, et al. Dynamic analysis of train-bridge system subjected to non-uniform seismic excitations [J].Earthquake Engineering and Structural Dynamics, 2006, 35: 1563-1579.

[2]Du X T, Xu Y L, Xia H. Dynamic interaction of bridge-train system under non-uniform seismic ground motion [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(1): 139-157.

[3]Yang Y B, Wu Y S. Dynamic stability of trains moving over bridges shaken by earthquakes [J]. Journal of Sound and Vibration, 2002, 258(1): 65-94.

[4]譚長建, 祝兵. 地震作用下高速列車與橋梁耦合振動分析[J]. 振動與沖擊, 2009, 28(1): 4-8.

TAN Chang-jian, ZHU Bing. Coupled vibration analysis of high speed train and bridge subjected to seismic excitation [J]. Journal of Vibration and Shock, 2009, 28(1): 4-8.

[5]Celibi M. Topographical and geological amplifications determined from strong-motion and aftershock records of the 3 March 1985 Chile earthquake [J]. Bulletin of the Seismological Society of America, 1987, 88(4): 1147-1167.

[6]Priestley M J N, Seible F, Calvi G M.Seismic design and retrofit of bridges [M]. New York: John Wiley & Sons Inc., 1996.

[7]Jibson R. Summary of research on the effects of topographic amplification of earthquake shaking on slope stability[R]. US Geological Survey, Open-file Report 87-268, Menlo Park, California, 1987.

[8]周國良. 河谷地形對多支撐大跨橋梁地震反應影響[D]. 哈爾濱: 中國地震局工程力學研究所, 2010.

[9]Zhou G L, Li X J, Qi X J. Seismic response analysis of continuous rigid frame bridge considering canyon topography effects under incident SV waves[J]. Earthquake Science, 2010, 23(1): 53-61.

[10]Jia H Y, Zhang D Y, Zheng S X, et al. Local site effects on a high-pier railway bridge under tridirectional spatial excitations: nonstationary stochastic analysis [J]. Soil Dynamic and Earthquake Engineering, 2013, 52: 55-69.

[11]郜新軍, 趙成剛, 劉秦. 地震波斜入射下考慮局部地形影響和土結動力相互作用的多跨橋動力響應分析 [J]. 工程力學, 2011, 28(11): 237-243.

GAO Xin-jun, ZHAO Cheng-gang, LIU Qin. Seismic response analysis of multi-span viaduct considering topographic effect and soil-structure dynamic interaction based on inclined wave [J]. Engineering Mechanics, 2011,28(11):237-243.

[12]Liu J B, Du Y X, Du X L, et al. 3D Viscous-spring artificial boundary in time domain [J]. Earthquake Engineering and Engineering Vibration, 2006, 5(1): 93-102.

[13]劉晶波, 呂彥東. 結構-地基動力相互作用問題分析的一種直接方法[J]. 土木工程學報, 1998, 31(3): 55-64.

LIU Jing-bo, Lü Yan-dong. A direct method for analysis of dynamic soil-structure interaction [J]. China Civil Engineering Journal, 1998, 31(3): 55-64.

[14]杜修力, 趙密. 基于黏彈性邊界的拱壩地震反應分析方法[J]. 水利學報, 2006, 37(9):1063-1069.

DU Xiu-li, ZHAO Mi. Analysis method for seismic response of arch dams in time domain based on viscous-spring artificial boundary condition [J]. Journal of Hydraulic Engineering, 2006, 37(9):1063-1069.

[15]杜修力. 工程波動理論與方法[M]. 北京: 科學出版社, 2009.

[16]Xia H, De Roeck G, Goicolea J M. Bridge vibration and controls: New research [M]. New York: Nova Science Publishers Inc., 2011.