基于時(shí)變AR模型的非平穩(wěn)非高斯隨機(jī)過程的數(shù)值模擬

第一作者李錦華男，博士, 講師, 碩士生導(dǎo)師，1981年12月生

通信作者陳水生男，博士, 教授, 碩士生導(dǎo)師，1968年6月生

基于時(shí)變AR模型的非平穩(wěn)非高斯隨機(jī)過程的數(shù)值模擬

李錦華1, 2,陳水生2,吳春鵬2,李建豐2

(1.華東交通大學(xué)鐵路環(huán)境振動(dòng)與噪聲教育部研究工程中心,南昌330013; 2.華東交通大學(xué)土木建筑學(xué)院,南昌330013)

摘要：為了有效地模擬具有目標(biāo)非平穩(wěn)、非高斯特征的隨機(jī)過程，提出了基于時(shí)變AR模型的非平穩(wěn)非高斯隨機(jī)過程的模擬方法。該方法首先需要建立實(shí)現(xiàn)非高斯與高斯隨機(jī)過程之間相互轉(zhuǎn)換的非線性平移關(guān)系，然而該非線性平移也會(huì)導(dǎo)致平移前后高斯與非高斯隨機(jī)過程的功率譜發(fā)生變化。因此該方法還需要進(jìn)一步建立平移前后高斯與非高斯隨機(jī)過程的功率譜或相關(guān)函數(shù)的轉(zhuǎn)換關(guān)系。然后，通過已建立的非線性平移，以及功率譜或相關(guān)函數(shù)的轉(zhuǎn)換關(guān)系，可將非平穩(wěn)非高斯隨機(jī)過程的模擬轉(zhuǎn)化成對(duì)非平穩(wěn)高斯隨機(jī)過程的模擬。而非平穩(wěn)高斯隨機(jī)過程可通過建立的時(shí)變AR模型進(jìn)行有效的模擬。最后將具有目標(biāo)非平穩(wěn)、非高斯特征的脈動(dòng)風(fēng)速模擬作為數(shù)值算例，驗(yàn)證了該方法模擬非平穩(wěn)非高斯隨機(jī)過程的有效性。

關(guān)鍵詞：時(shí)變AR模型；數(shù)值模擬；非平穩(wěn)隨機(jī)過程；非高斯；脈動(dòng)風(fēng)速

基金項(xiàng)目：國(guó)家自然科學(xué)基金項(xiàng)目(11162005);江西省自然科學(xué)基金項(xiàng)目(20132BAB216003)

收稿日期：2015-01-07修改稿收到日期：2015-03-11

中圖分類號(hào):TU311

文獻(xiàn)標(biāo)志碼：A

DOI:10.13465/j.cnki.jvs.2015.17.024

Abstract:In order to simulate effectively a stochastic process possessing given non-stationary non-Gaussian features, a method to simulate a non-stationary non-Gaussian stochastic process based on a time-varying AR model was proposed here. Firstly, it was necessary to establish a nonlinear translation relationship to realize mutual conversion between a non-Gaussian and a Gaussian one. Meanwhile, the power spectra both the non-Gaussian and the Gaussian random processes were different due to the nonlinear translation. Furthermore, the transformation relationship between their power spectra or correlation functions was established. Then, the simulation of a non-stationary non-Gaussian stochastic process was converted into a simulation of a non-stationary Gaussian random process by utilizing the nonlinear translation relationship and the transformation relationship of their power spectra or correlation functions constructed above. The non-stationary Gaussian random process was effectively simulated with a presented time-varying AR model. Finally, taking the simulation of a fluctuating wind velocity possessing target non-stationary non-Gaussian characteristics as a numerical example, the effectiveness of the method to simulate a non-stationary non-Gaussian random process was verified.

Simulation of non-stationary non-Gaussian stochastic process based on a time-varying AR model

LIJin-hua1, 2,CHENShui-sheng2,WUChun-peng2,LIJian-feng2(1. MOE Engineering Research Center of Railway Environmental Vibration and Noise, East China Jiaotong University, Nanchang 330013, China;2. College of Civil Engineering,East China Jiaotong University, Nanchang 330013, China)

Key words:time-varying AR model; numerical simulation; non-stationary stochastic process; non-Gaussian; fluctuating wind velocity

計(jì)算機(jī)技術(shù)的快速發(fā)展，使得運(yùn)用計(jì)算隨機(jī)力學(xué)解決不確定性系統(tǒng)的分析成為可能[1]。在進(jìn)行不確定性系統(tǒng)分析過程中，需要首先獲取輸入的不確定性隨機(jī)參量。基于蒙特卡洛Monte-Carlo的隨機(jī)模擬技術(shù)[2]，使得人工模擬系統(tǒng)的隨機(jī)輸入得到了廣泛的應(yīng)用。在模擬產(chǎn)生具有指定目標(biāo)特征的隨機(jī)過程中，不確定性隨機(jī)參量常被假定為平穩(wěn)高斯、非平穩(wěn)高斯隨機(jī)過程來(lái)模擬，這個(gè)假定極大地簡(jiǎn)化模擬計(jì)算過程。在自然界中，不確定性系統(tǒng)的隨機(jī)參量如工程結(jié)構(gòu)上的風(fēng)壓、結(jié)構(gòu)與機(jī)械工程中的幾何特性和材料特性、巖土工程中的土壤特性、海洋波浪的隨機(jī)激勵(lì)等均具有非高斯的特征[3]。為了有效地研究分析隨機(jī)激勵(lì)下的系統(tǒng)響應(yīng)，具有目標(biāo)特征的平穩(wěn)非高斯乃至非平穩(wěn)非高斯隨機(jī)過程的有效模擬逐漸受到廣泛關(guān)注。非平穩(wěn)非高斯隨機(jī)過程不僅具有相關(guān)函數(shù)或功率譜密度隨時(shí)間變化的特征，而且每一時(shí)刻的概率密度函數(shù)分布呈現(xiàn)出非高斯分布的特征。高斯隨機(jī)過程的概率密度函數(shù)可以完全由前兩階統(tǒng)計(jì)參數(shù)( 即均值和方差) 來(lái)描述。而對(duì)于非高斯隨機(jī)過程，特別是非平穩(wěn)非高斯隨機(jī)過程，可采用高階統(tǒng)計(jì)參數(shù)(特別是三階和四階統(tǒng)計(jì)參數(shù)，即偏度和峰度)對(duì)非高斯概率密度函數(shù)的特征進(jìn)行描述。模擬非平穩(wěn)非高斯隨機(jī)過程，需要模擬具有目標(biāo)時(shí)變特征的相關(guān)函數(shù)或功率譜，以及目標(biāo)非高斯特征。因此，非平穩(wěn)非高斯隨機(jī)過程的模擬，可先通過模擬生成某一非平穩(wěn)高斯隨機(jī)過程，然后再將該非平穩(wěn)高斯隨機(jī)過程經(jīng)過非線性平移生成具有目標(biāo)特征的非平穩(wěn)非高斯隨機(jī)過程。

運(yùn)用Monte-Carlo思想模擬隨機(jī)過程主要有兩大類方法，即譜表示法和線性濾波法。譜表示方法的模擬精度較高，但模擬效率較低[4]。而線性濾波法盡管模擬精度較低，但計(jì)算量小、速度快，被廣泛用于工程領(lǐng)域隨機(jī)過程的模擬[6]。Decolatis等[6]對(duì)桅桿結(jié)構(gòu)由不同方法得到的風(fēng)速時(shí)程作用下的結(jié)構(gòu)響應(yīng)結(jié)果作出比較后，建議采用AR模型模擬互相相關(guān)多重脈動(dòng)風(fēng)速時(shí)程。Owen等[7]采用AR模型模擬了平穩(wěn)隨機(jī)風(fēng)荷載，并用于斜拉橋的風(fēng)振響應(yīng)分析。Saramas等[8]采用ARMA模型模擬了多變量平穩(wěn)隨機(jī)過程。以上模擬主要針對(duì)的是平穩(wěn)高斯隨機(jī)過程的模擬。張文福等[9]通過時(shí)變函數(shù)均勻調(diào)制基于AR模型的平穩(wěn)脈動(dòng)風(fēng)速來(lái)生成了下?lián)舯┝鞣瞧椒€(wěn)脈動(dòng)風(fēng)速。Li等[10]通過建立AR和ARMA模型輸入與輸出統(tǒng)計(jì)特征之間的關(guān)系，建立了基于AR和ARMA模型的非高斯平穩(wěn)隨機(jī)過程模擬，并通過非高斯平穩(wěn)脈動(dòng)風(fēng)荷載的模擬驗(yàn)證了模擬的有效性。本文將進(jìn)一步探討基于時(shí)變AR模型的非平穩(wěn)非高斯隨機(jī)過程的有效模擬。

1非平穩(wěn)高斯隨機(jī)過程的時(shí)變AR模型

設(shè)時(shí)變AR模型階數(shù)為p，非平穩(wěn)高斯隨機(jī)過程模擬樣本點(diǎn)數(shù)為N，采樣時(shí)間間隔為Δt，則基于時(shí)變AR(p)模型的非平穩(wěn)高斯隨機(jī)過程模擬公式可表示為：

(1)

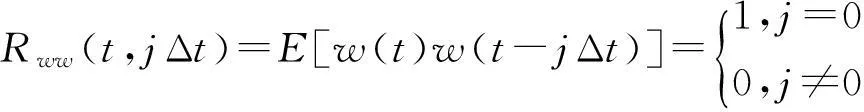
1.1時(shí)變模型系數(shù)Ai(t)的確定

在某時(shí)刻t=t′時(shí)，有

(2)

對(duì)于Ai(t′)的確定，將式(2)兩邊同時(shí)右乘f(t′-jΔt)，并取數(shù)學(xué)期望，有

E[f(t′)f(t′-jΔt)]=

E[L(t′)w(t′)f(t′-jΔt)]

(3)

Rff(t′,jΔt)=

對(duì)于右二項(xiàng)，Rwf(t′,jΔt)可理解為w(t′)與f(t′-jΔt)的互相關(guān)函數(shù)。w(t)為該系統(tǒng)的輸入，而f(t)為系統(tǒng)的輸出。當(dāng)前的輸出只依賴于當(dāng)前和過去的輸入，而與將來(lái)的輸入無(wú)關(guān)，因此w(t′)與f(t′-jΔt)互相獨(dú)立，故

Rwf(t′,jΔt)=0

(5)

將式(5)代入式(4)，可確定Ai(t′)

(6)

其展開式為

1.2時(shí)變模型系數(shù)L(t)的確定

在某時(shí)刻t=t′時(shí)，將式(2)兩邊同時(shí)右乘w(t′)，并取數(shù)學(xué)期望，有

Rfw(t′,0)=

(7)

當(dāng)前輸入w(t′)與過去輸出f(t′-iΔt)互相獨(dú)立，則

Rfw(t′-iΔt,iΔt)=0

(8)

將式(8)代入式(7)，可得

Rfw(t′,0)=L(t′)Rww(t′,0)

(9)

根據(jù)白噪聲的特性，有Rww(t′,0)=1，則

Rfw(t′,0)=L(t′)

(10)

再一次將式(2)兩邊同時(shí)右乘f(t′)，并取數(shù)學(xué)期望，有

L(t′)Rwf(t′,0)

(11)

又因?yàn)?/p>

Rwf(t′,0)=E[w(t′)f(t′)]=

E[f(t′)w(t′)]=Rfw(t′,0)

(12)

將式(10)和(12)代入式(11)，有

Rff(t′,0)=

(13)

令A(yù)0(t′)=-1，則

(14)

因此，時(shí)變模型系數(shù)Ai(t′)和L(t′)，t′=1,2,3,…，可分別根據(jù)式(6)和(14)來(lái)確定。

2非線性平移過程

非高斯隨機(jī)過程y(t)可通過潛在高斯隨機(jī)過程f(t)進(jìn)行非線性平移轉(zhuǎn)換。

h4(f3(t)-3f(t))]

(15)

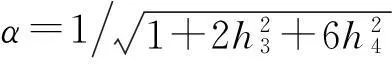
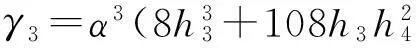
(16)

(17)

為了使得式(15)的非線性平移可逆，形狀系數(shù)需滿足

(18)

則非高斯隨機(jī)過程的偏度和峰度需滿足下列關(guān)系

(19)

當(dāng)具有目標(biāo)功率譜的標(biāo)準(zhǔn)化高斯隨機(jī)過程，經(jīng)過式(15)非線性平移前后，生成的標(biāo)準(zhǔn)化非高斯隨機(jī)過程的功率譜必然發(fā)生非線性變化。因此，標(biāo)準(zhǔn)化非高斯隨機(jī)過程的目標(biāo)功率譜不能直接作為高斯隨機(jī)過程目標(biāo)功率譜進(jìn)行模擬。為此，需要建立標(biāo)準(zhǔn)化非高斯隨機(jī)過程的目標(biāo)功率譜與高斯隨機(jī)過程目標(biāo)功率譜的轉(zhuǎn)化關(guān)系。根據(jù)Pristley的“進(jìn)化譜”理論[11]，一零均值非平穩(wěn)隨機(jī)過程可表示為：

(20)

式中:A(ω,t)為非均勻調(diào)制函數(shù)；Z(ω)為一正交過程，且滿足

E[dZ(ω)]=0

(21)

E[dZ*(ω)dZ(ω′)]=J(ω)δ(ω-ω′)dωdω′

(22)

其中:*表示共軛，δ為狄拉克函數(shù)。則非平穩(wěn)隨機(jī)過程的均值為

(23)

相關(guān)函數(shù)為

Rff(t,τ)=E[f*(t)f(t+τ)]=

τ)e-iωteiω′(t+τ)E[dZ*(ω)dZ(ω′)]=

(24)

當(dāng)τ=0時(shí)，

(25)

因此，進(jìn)化譜S(ω,t)可通過一時(shí)頻函數(shù)A(ω,t)對(duì)功率譜的非均勻調(diào)制來(lái)表示[12]，即

(26)

根據(jù)式(24)和式(26)，可建立非平穩(wěn)隨機(jī)過程的相關(guān)函數(shù)與時(shí)變功率譜之間的關(guān)系

Rff(t,τ)=E[f*(t)f(t+τ)]=

(27)

根據(jù)相關(guān)函數(shù)與功率譜之間的相互轉(zhuǎn)換關(guān)系，非高斯隨機(jī)過程與高斯隨機(jī)過程的目標(biāo)功率譜之間的非線性關(guān)系，可通過目標(biāo)相關(guān)函數(shù)之間的非線性關(guān)系進(jìn)行表達(dá)。

根據(jù)式(15)的非線性平移，標(biāo)準(zhǔn)化的非高斯隨機(jī)過程的相關(guān)函數(shù)可表示為

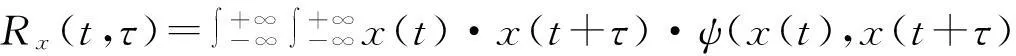
ρx(t,τ))·dx(t)·dx(t+τ)=

α[f(t+τ)+h3(f2(t+τ)-1)+

h4(f3(t+τ)-3f(t+τ))]×

φ(f(t),f(t+τ),ρf(t,τ))·df(t)·df(t+τ)

(28)

其中:ψ為具有相關(guān)系數(shù)ρx的兩非高斯隨機(jī)過程的聯(lián)合概率密度函數(shù)；φ為具有相關(guān)系數(shù)ρf的兩高斯隨機(jī)過程的聯(lián)合概率密度函數(shù)。

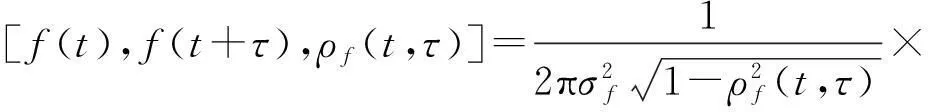
(29)

而相關(guān)函數(shù)與相關(guān)系數(shù)的轉(zhuǎn)化關(guān)系為

R(t,τ)=ρ(t,τ)·σ2

(30)

根據(jù)式(28)～(30)，可建立非高斯隨機(jī)過程與高斯隨機(jī)過程的相關(guān)系數(shù)或相關(guān)函數(shù)之間的轉(zhuǎn)換關(guān)系。

3非平穩(wěn)非高斯風(fēng)荷載的數(shù)值模擬

為了驗(yàn)證上述非平穩(wěn)非高斯隨機(jī)過程模擬方法的有效性，本節(jié)將以具有非平穩(wěn)非高斯特征脈動(dòng)風(fēng)速的模擬作為數(shù)值算例。在數(shù)值模擬過程中，脈動(dòng)風(fēng)速的目標(biāo)非平穩(wěn)特征主要表現(xiàn)在功率譜隨時(shí)間變化的時(shí)變功率譜S(t,ω)，該時(shí)變功率譜可采用Davenport非均勻調(diào)制函數(shù)[13]

(31)

調(diào)制Davenport譜

(32)

目標(biāo)非高斯特征主要通過偏度γ3、峰度γ4來(lái)考慮，分別假定為偏度γ3=-1.2、峰度γ4=8。根據(jù)式(16)、(17)可進(jìn)一步確定非線性平移變換的形狀系數(shù)h3=-0.140 6、h4=0.075 3，以及參數(shù)α=0.965 1。由該非線性平移變換可知，在生成具有目標(biāo)非高斯特征的非平穩(wěn)隨機(jī)過程之前，首先需要模擬潛在的非平穩(wěn)高斯隨機(jī)過程。根據(jù)式(27)～(30)，可建立非平穩(wěn)非高斯隨機(jī)過程與潛在的非平穩(wěn)高斯隨機(jī)過程之間的相關(guān)系數(shù)轉(zhuǎn)換關(guān)系如1圖所示。

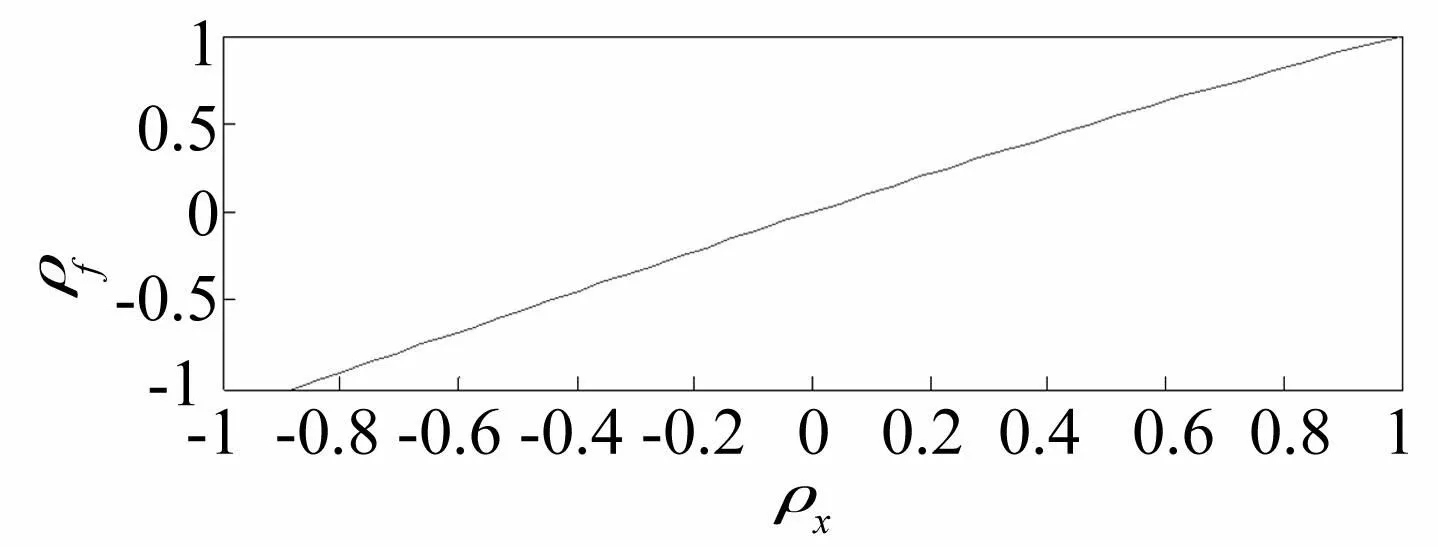
圖1　高斯與非高斯隨機(jī)過程相關(guān)系數(shù)之間的轉(zhuǎn)換關(guān)系 Fig.1 The transformation relationship of the correlation coefficients between Gaussian and non-Gaussian random processes

基于時(shí)變AR模型生成潛在的非平穩(wěn)高斯隨機(jī)過程見圖2，并將其經(jīng)過非線性平移變換生成的非平穩(wěn)非高斯脈動(dòng)風(fēng)速見圖3。對(duì)多組脈動(dòng)風(fēng)速樣本進(jìn)行功率譜估計(jì)，其估計(jì)譜(見圖4)明顯具有如圖5所示的目標(biāo)時(shí)變功率譜的時(shí)變特征。任意時(shí)刻估計(jì)譜與目標(biāo)譜的對(duì)比見圖6，在該圖中四個(gè)任意時(shí)刻的估計(jì)譜均與目標(biāo)譜基本吻合，且相應(yīng)的相關(guān)函數(shù)也與目標(biāo)相吻合見圖7。在時(shí)間上統(tǒng)計(jì)平均的功率譜、相關(guān)函數(shù)也均與目標(biāo)基本吻合見圖8、9。因此，模擬的脈動(dòng)風(fēng)速具有目標(biāo)特征的非平穩(wěn)特性。

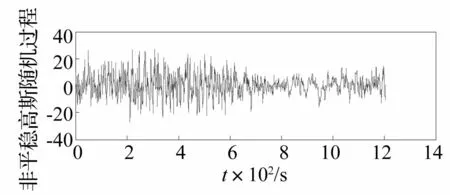
圖2　模擬的非平穩(wěn)高斯隨機(jī)過程 Fig.2 Thesimulated non-stationary Gaussian stochastic process

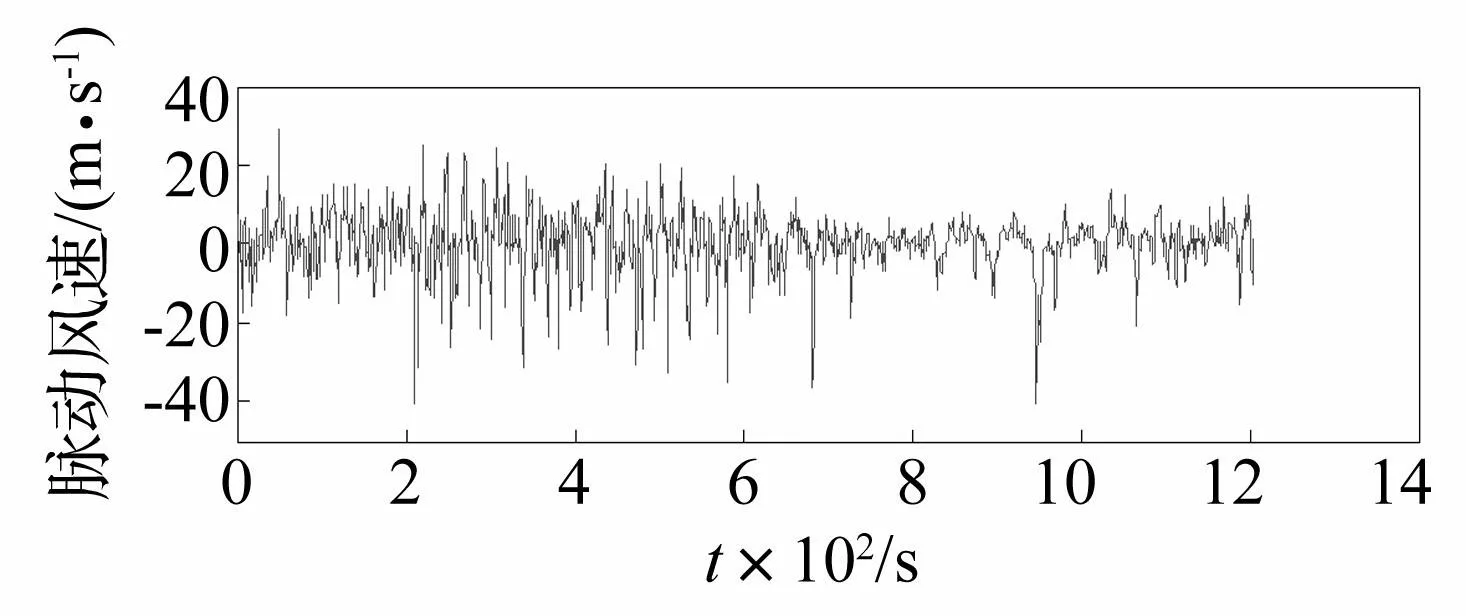
圖3　非線性平移生成的非平穩(wěn)非高斯脈動(dòng)風(fēng)速 Fig.3 Thegenerated non-stationary non-Gaussian fluctuating wind velocity through nonlinear translation

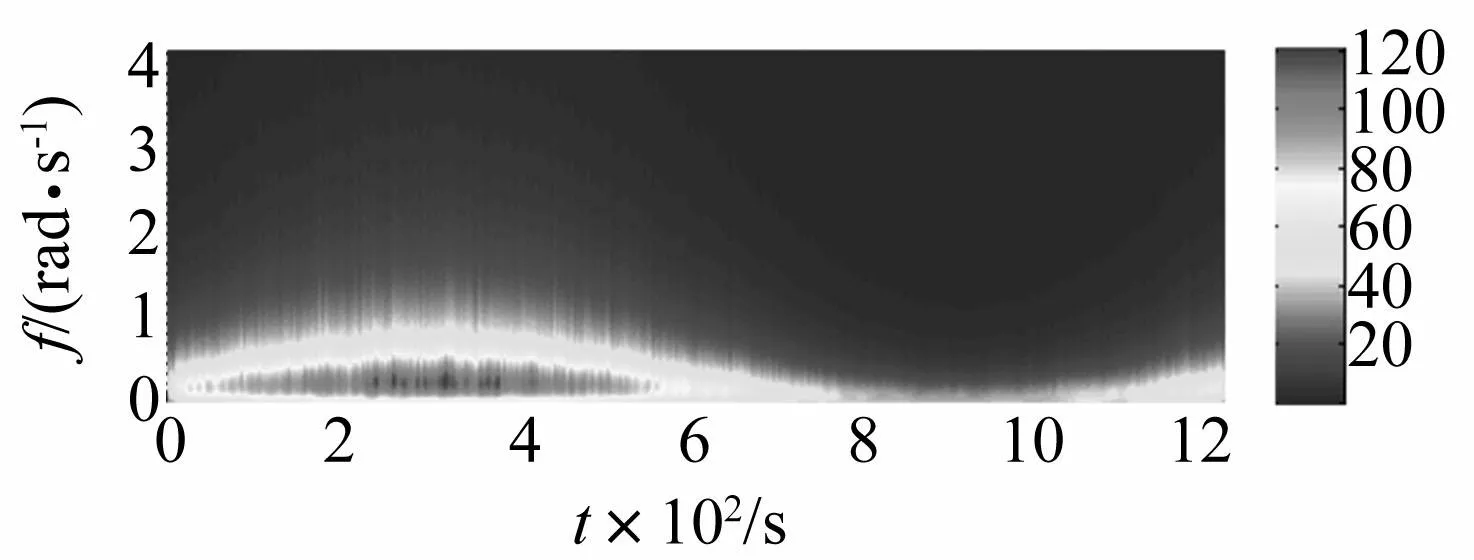
圖4　脈動(dòng)風(fēng)速樣本時(shí)變譜 Fig.4 The time-varying power spectrum of the fluctuating wind velocity

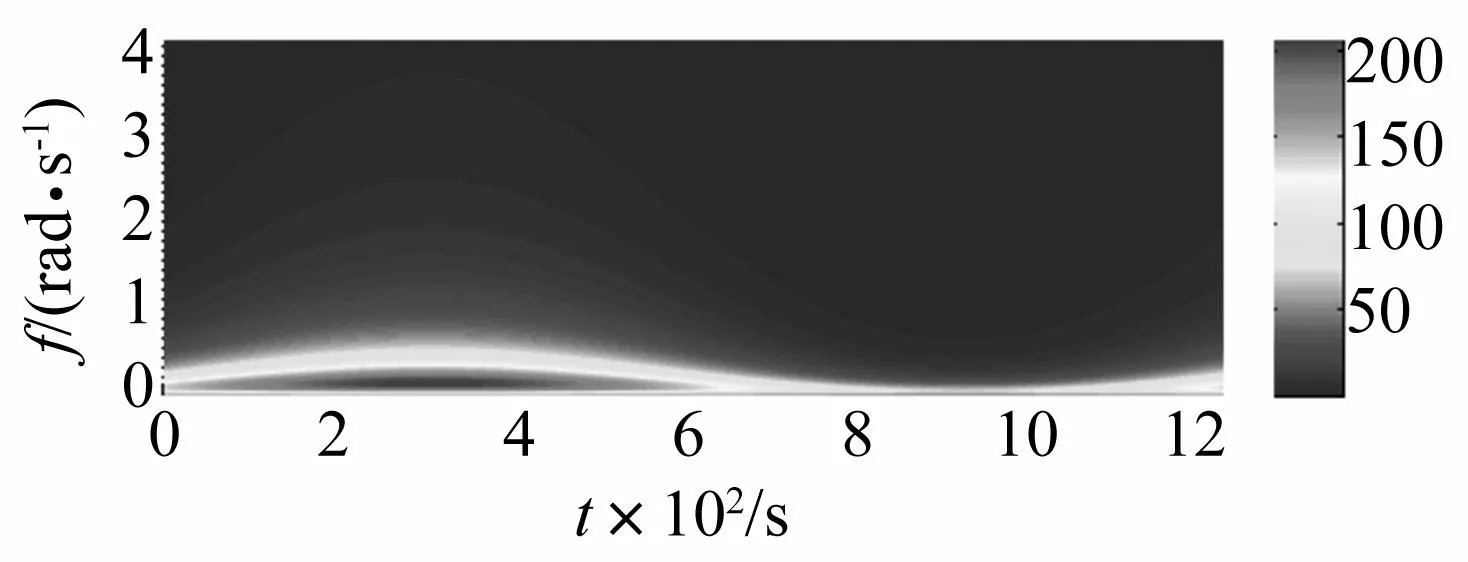
圖5　脈動(dòng)風(fēng)速的目標(biāo)時(shí)變譜 Fig.5 The target power spectrum of the fluctuating wind velocity

圖6　脈動(dòng)風(fēng)速瞬時(shí)估計(jì)譜與目標(biāo)譜的對(duì)比 Fig.6 Instantaneous power spectrums of the fluctuating wind velocity with regard to the corresponding targets

圖7　脈動(dòng)風(fēng)速的瞬時(shí)相關(guān)函數(shù)與目標(biāo)相關(guān)函數(shù)的對(duì)比 Fig.7 Instantaneous correlation functions of the fluctuating wind velocity with regard to the corresponding targets

為了進(jìn)一步說(shuō)明模擬的有效性，圖10、11展示了脈動(dòng)風(fēng)速高階統(tǒng)計(jì)特征值(即偏度值、峰度值)的估計(jì)。圖中所示的脈動(dòng)風(fēng)速的任意時(shí)刻偏度和峰度盡管都在其各自均值附近有一定的離散性，但其方差均較小分別為0.2和2.4；而其偏度均值為-1.18接近于目標(biāo)偏度值-1.2，峰度均值7.7也接近于目標(biāo)峰度值8，說(shuō)明了模擬的脈動(dòng)風(fēng)速具有目標(biāo)非高斯特征。因此，模擬的脈動(dòng)風(fēng)速具有目標(biāo)非平穩(wěn)、非高斯特征，說(shuō)明了非平穩(wěn)非高斯隨機(jī)過程模擬方法的有效性。該方法建立在AR模型基礎(chǔ)上，受到AR模型本身模擬精度的影響，盡管在模擬中存在一定誤差，但在工程中是可以接受的。因此，該方法可應(yīng)用于精度要求較低的工程中。

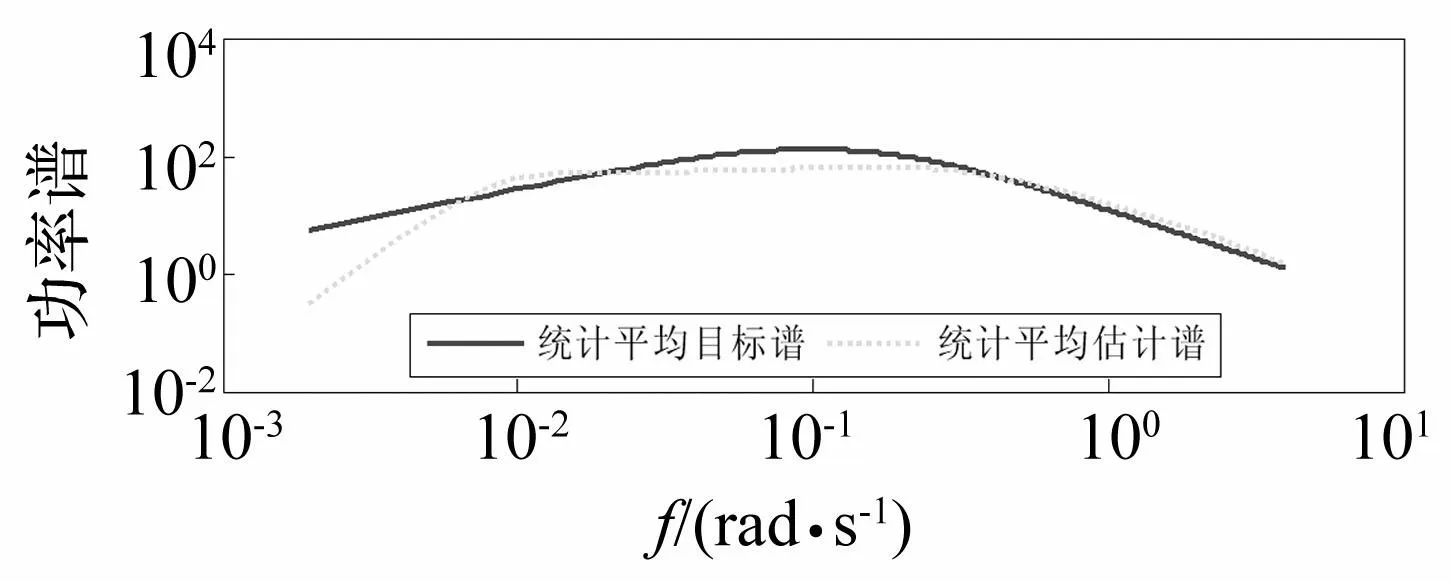
圖8　脈動(dòng)風(fēng)速統(tǒng)計(jì)平均估計(jì)譜與目標(biāo)譜的對(duì)比 Fig.8 Temporal average power spectrum of the fluctuating wind velocity with regard to the corresponding target

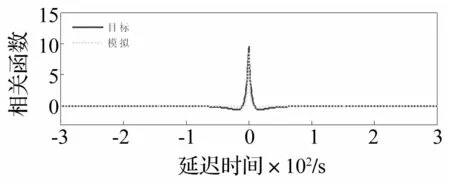
圖9　脈動(dòng)風(fēng)速統(tǒng)計(jì)平均相關(guān)函數(shù)與目標(biāo)相關(guān)函數(shù)的對(duì)比 Fig.9 Temporal average correlation function of the fluctuating wind velocity with regard to the corresponding target

圖10　脈動(dòng)風(fēng)速的偏度 Fig.10 The skewness of the fluctuating wind velocity

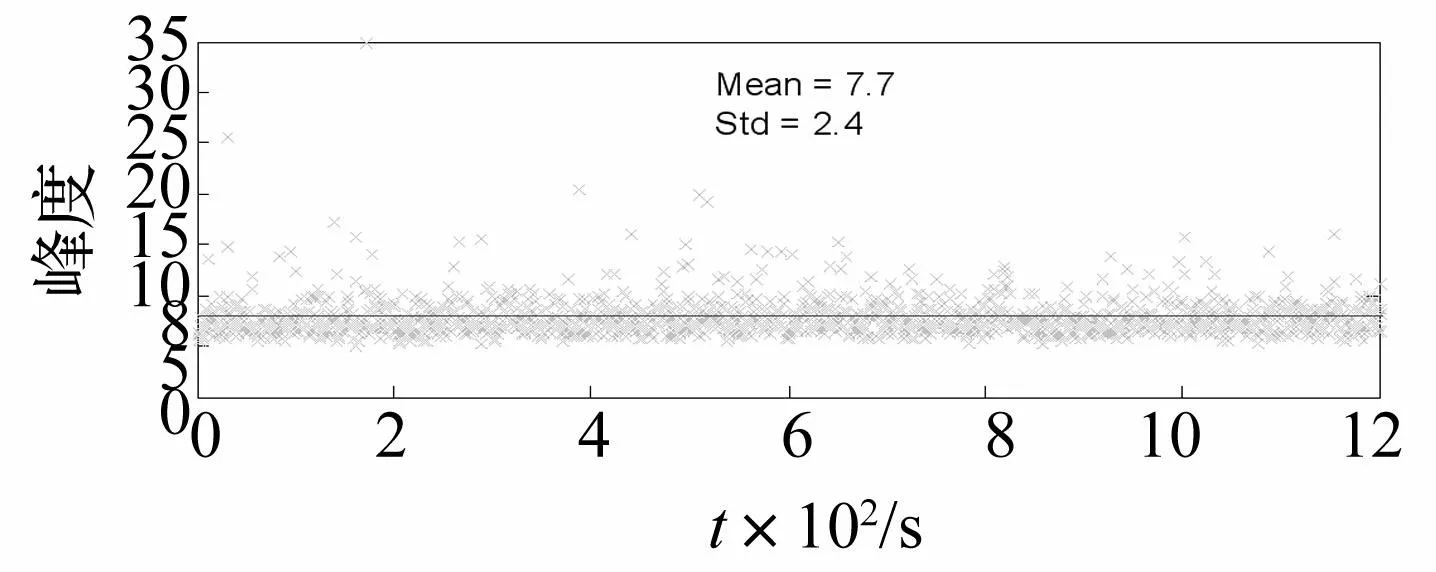
圖11　脈動(dòng)風(fēng)速的峰度 Fig.11 The kurtosis of the fluctuating wind velocity

4結(jié)論

為了有效地模擬具有目標(biāo)非平穩(wěn)、非高斯特征的隨機(jī)過程，本文提出了基于時(shí)變AR模型的非平穩(wěn)非高斯隨機(jī)過程的模擬方法。該方法通過建立非高斯與高斯隨機(jī)過程之間相互轉(zhuǎn)換的非線性平移關(guān)系，以及非線性平移前后高斯與非高斯隨機(jī)過程的功率譜或相關(guān)函數(shù)的轉(zhuǎn)換關(guān)系，可將非平穩(wěn)非高斯隨機(jī)過程轉(zhuǎn)化為非平穩(wěn)高斯隨機(jī)過程的模擬。而非平穩(wěn)高斯隨機(jī)過程可通過建立的時(shí)變AR模型進(jìn)行有效的模擬。為了驗(yàn)證該方法的有效性，文中進(jìn)行了具有目標(biāo)非平穩(wěn)非高斯特征的脈動(dòng)風(fēng)速模擬。脈動(dòng)風(fēng)速的時(shí)變功率譜估計(jì)表明：模擬生成的脈動(dòng)風(fēng)速樣本的時(shí)變功率譜和相關(guān)函數(shù)均與目標(biāo)基本吻合，模擬的脈動(dòng)風(fēng)速具有目標(biāo)特征的非平穩(wěn)特性。脈動(dòng)風(fēng)速高階統(tǒng)計(jì)特征值(即偏度值、峰度值)的估計(jì)表明：非平穩(wěn)脈動(dòng)風(fēng)速的任意時(shí)刻偏度和峰度在其各自均值附近有一定的離散性，但其方差均較小；而其偏度均值、峰度均值都非常接近于目標(biāo)值。因此，模擬的脈動(dòng)風(fēng)速具有目標(biāo)非平穩(wěn)與非高斯特征，說(shuō)明了非平穩(wěn)非高斯隨機(jī)過程模擬方法的有效性。

參考文獻(xiàn)

[1]Acharjee S, Zabaras N. Uncertainty propagation in finite deformations-a spectral stochastic Lagrangian approach [J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195: 2289-2312.

[2]Spanos P D, Zeldin B A. Monte Carlo treatment of random fields: a broad perspective [J]. Applied Mechanics Reviews, 1998, 51:219-237.

[3]李錦華, 陳水生. 非高斯隨機(jī)過程模擬與預(yù)測(cè)的研究進(jìn)展[J].華東交通大學(xué)學(xué)報(bào), 2011, 28(6):1-6.

LI Jin-hua, CHEN Shui-sheng. Advances in simulation and prediction of non-gaussian stochastic processes[J]. Journal of East China Jiaotong University, 2011, 28(6):1-6.

[4]李錦華, 李春祥, 申建紅. 非平穩(wěn)脈動(dòng)風(fēng)速的數(shù)值模擬[J]. 振動(dòng)與沖擊, 2009, 28(1):18-23.

LI Jin-hua, LI Chun-xiang, SHEN Jian-hong. Numerical simulation of non-stationary fluctuating wind velocity[J]. Journal of Vibration and Shock, 2009, 28(1):18-23.

[5]舒新玲, 周岱. 風(fēng)速時(shí)程AR模型及其快速實(shí)現(xiàn)[J].空間結(jié)構(gòu),2003,9(4):27-32.

SHU Xin-ling, ZHOU Dai. AR model of wind speed time series and its rapid implementation[J]. Spatial Structures, 2003, 9(4):27-32.

[6]Deodatis G, Micaletti R C. Simulation of highly skewed non-Gaussian stochastic processes [J]. Journal of Engineering Mechanics ASCE, 2001, 127(12): 1284-1295.

[7]Owen J S, Eccles B J, Choo B S, et al. The application of auto-regressive time series modeling for the time-frequency analysis of civil engineering structures [J]. Engineering Structures, 2001,23:521-536.

[8]Samaras E, Shinozuka M, Tsurui A. ARMA representation of random process [J].Journal of Engineering Mechanics ASCE, 1985, 111(3): 449-461.

[9]張文福, 謝丹, 劉迎春, 等. 下?lián)舯┝骺臻g相關(guān)性風(fēng)場(chǎng)模擬[J]. 振動(dòng)與沖擊, 2013, 32(10): 12-16.

ZHANG Wen-fu, XIE Dan, LIU Ying-chun, et al. Simulation of downburst wind field with spatial correlation[J]. Journal of Vibration and Shock, 2013, 32(10): 12-16.

[10]Li J H, Li C X. Simulation of non-gaussian stochastic process with target power spectral density and lower-order moments [J]. Journal of Engineering Mechanics ASCE, 2012, 138(5):391-404.

[11]Priestley M B. Power spectral analysis of non-stationary random processes [J]. Journal of Sound and Vibration, 1967, 6:86-97.

[12]Liang J, Chaudhuri S R, Shinozuka M. Simulation of non-stationary stochastic processes by spectral representation [J]. Journal of Engineering Mechanics ASCE, 2007, 133 (6): 616-627.

[13]李錦華, 吳春鵬, 陳水生. 下?lián)舯┝鞣瞧椒€(wěn)脈動(dòng)風(fēng)速的數(shù)值模擬[J].振動(dòng)與沖擊, 2014, 33(14):54-60.

LI Jin-hua, WU Chun-peng, CHEN Shui-sheng. Simulation of non-stationary fluctuating wind velocity in downburst[J]. Journal of Vibration and Shock, 2014, 33(14):54-60.