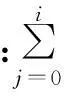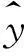壓電微動平臺的定位控制

第一作者崔玉國男，教授,博士生導師，1971年5月生

壓電微動平臺的定位控制

崔玉國, 朱耀祥, 馬劍強, 方凡

(1. 寧波大學機械工程與力學學院，浙江寧波315211;2.浙江省零件軋制成型技術研究重點實驗室，浙江寧波315211)

摘要：為使壓電微動平臺定位速度快、定位精度高，采用復合控制方法來對其進行定位控制。基于保證模型精度并使精度在整個閾值區間變化盡量均勻的要求，來使閾值最優化，進而建立了壓電微動平臺的遲滯模型。基于所建平臺遲滯模型，設計了其前饋控制器；為抑制平臺的超調，在常規數字增量式PID中引入濾波器設計了其反饋控制器；將前饋控制與PID反饋控制相結合，設計了平臺的復合控制器。實驗結果表明：所建平臺遲滯模型僅有7個算子，且均為有效算子，在16.3 μm的最大實測位移下，模型最大誤差為0.208 μm；在復合控制作用下，平臺達到5 μm目標值的響應時間為0.173 s，雖慢于前饋控制，但明顯快于PID反饋控制；在最大位移為17.155 μm的參考輸入作用下，若不考慮傳感器噪聲，平臺的定位誤差幾乎為零。

關鍵詞：壓電微動平臺；遲滯模型；前饋控制；PID反饋控制；復合控制

基金項目：國家自然科學基金項目(51175271)；教育部留學回國人員科研啟動基金資助項目；浙江省高等學校中青年學科帶頭人學術攀登項目(Pd2013091);浙江省自然科學基金(LY12E09001)

收稿日期：2014-12-03修改稿收到日期：2015-03-11

中圖分類號:TH212；TH213.3

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2015.17.011

Abstract:To achieve high positioning speed and high positioning accuracy for a piezoelectric micro-positioning stage, a compound position control method was investigated. A hysteresis model of the micro-positioning stage was established. The threshold value was optimized by ensuring the model accuracy and the uniformity of the threshold interval changes. Then a feedforward controller based on the hysteresis model was developed. In order to suppress the overshoot of the stage, a filter was introduced in a PID feedback controller based on the conventional digital incremental PID. Further, a compound controller combining the feedforward controller with the PID feedback controller was developed. The experimental results showed that the developed model has only 7 effective operators; the model’s maximum error is 0.208 μm; under the maximum measured displacement of 16.3 μm; under the compound control, the response time of the micro-positioning stage to reach the traget value of 5 μm is 0.173 s, it is slower than that under feedforward control, but significantly faster than that under PID feedback control; regardless of the sensor noise, the position error of the stage is almost zero under the reference input action with the maximum displacement of 17.155 μm.

Position control for a piezoelectric micro-positioning stage

CUIYu-guo,ZHUYao-xiang,MAJian-qiang,FANGFan(1. College of Mechanical Engineering and Mechanics, Ningbo University, Ningbo 315211, China;2.Zhejiang Provincial Key Lab of Part Rolling Technology, Ningbo University, Ningbo 315211, China)

Key words:micro-positioning stage; hysteresis model; feedforward control; PID feedback control; compound control

微動平臺是一種高精度、高分辨率以及小行程的微位移機構，被用于實現精密加工中的微進給及誤差補償、精密測試中的微調節、光纖對接中的微對準等[1]。壓電微動平臺采用壓電陶瓷執行器驅動，體積小、剛度高、頻響快、分辨力高，從而獲得了更加廣泛的應用。

由于壓電陶瓷執行器具有遲滯非線性，從而使其驅動的微動平臺產生定位誤差，不利于微動平臺整體性能的發揮，這就需要建立壓電執行器或壓電微動平臺的遲滯模型，采用相應的控制方法來消除其遲滯誤差，提高其定位精度。描述壓電執行器或壓電微動平臺遲滯非線性的模型有Preisach模型[2-5]、PI(Prandtl-Ishilinskii)模型[6-9]、廣義Maxwell滑動模型[10]、變形狀增益因子模型[11]、變比模型[12]、坐標變換模型[13]等。Preisach模型通過多個遲滯算子的線性迭加來描述對象的遲滯特性，精度較高，但需要進行積分運算，不利于模型參數的辨識。PI模型是Preisach模型的改進，它將Preaisach模型離散化，并將遲滯算子改為斜坡函數，從而使模型算法簡單、運算量小、精度更高、便于求逆。廣義Maxwell滑動模型用多對無質量的線性彈簧-滑塊的輸入輸出特性來描述對象的遲滯特性，物理概念清晰，但算法復雜，模型參數辨識困難。變形狀增益因子模型需要時刻改變形狀增益因子的大小，給其應用帶來了不便。變比模型相對簡單、比較實用，但若第二升回程及其后的遲滯環不完全位于第一升回程的遲滯環內時，便無法描述對象在整個運動范圍內的遲滯特性。坐標變換模型表達式簡單、參數個數少、只用第一個升回程的實測值便可實現對任意升回程各點的跟蹤，但求擬運算相對復雜。

關于壓電微動平臺的定位控制方法，目前常用的有前饋控制[14]、PID控制[15]、模糊控制[16]、神經網絡控制[17]、魯棒控制[18]、自適應控制[19]、獨立模態控制[20]等，以及將這些方法相結合的復合控制[5, 21]。前饋控制屬于開環控制，它先預估可能出現的偏差，并進行相應的補償，從而使被控對象的響應更及時，但它不能完全消除穩態誤差，且控制精度取決于模型精度。PID控制屬于反饋控制，它通過對系統偏差的比例、積分與微分的組合來糾正系統偏差，可完全消除穩態誤差，參數少、技術成熟、易于實現。模糊控制是基于模糊推理的一類控制方法，適用于不確定參數系統和復雜系統的控制。神經網絡控制是類似于動物神經網絡結構特征的、并行處理信息的控制方法，具有很強的容錯性。魯棒控制是在變參數情況下仍保持系統某些特性的一種控制方法。自適應控制是在運行過程中不斷提取模型信息，自動使模型逐漸完善，從而使控制效果接近最優的一種控制方法。獨立模態控制針對被控對象的各階模態分別設計控制算法，對抑制被控對象的振動具有不錯的效果。在上述這些控制方法中，單一控制方法簡單，但難以獲得良好的綜合控制性能；復合控制方法略為復雜，但可獲得良好的綜合控制效果。

本文在對傳統PI模型進行改進并建立壓電微動平臺遲滯模型的基礎上，將具有較快響應速度的前饋控制與可完全消除穩態誤差的反饋控制相結合來設計壓電微動平臺的復合定位控制器，以使其具有良好的定位性能，即定位速度快、定位精度高。

1微動平臺定位控制器設計

1.1前饋控制器設計

前饋控制是基于模型的控制，下面在建立壓電微動平臺遲滯模型的基礎上來設計其前饋控制器。

1.1.1微動平臺遲滯建模

圖1　Backlash算子 Fig.1 Backlash operator

由于PI模型表達式簡單、參數少、求逆容易，故本文采用PI模型來建立壓電微動平臺的遲滯模型。PI模型的基本運算單元為Backlash算子，見圖1，Backlash算子的函數表達式為：

式中:y、x分別為Backlash算子的輸出、輸入，r、w分別為Backlash算子的閾值、權重。

為運算方便，Backlash算子函數常用數值迭代的形式來描述[6]，即：

y(t)=Hr,w[x(t),y(0)]=wmax{x(t)-r,

min[x(t)+r,y(t-T)]}

(2)

式中:T為采樣周期。

式(2)的初始條件為：

y(0)=wmax{x0-r,min(x0+r,y0)}

(3)

式中:x0=x(0)，y0為Backlash算子的初始值，通常取為0。

n個閾值不同、權重不同的Backlash算子線性疊加即可構成被描述對象的遲滯模型，即：

min[x(t)+ri,yi(t-T)]}=WTHr[x,y0]

(4)

式中:0=r0

式(4)中的ri、wi確定后，便可求得被描述對象的PI遲滯模型。而ri、wi的求解過程如下：

圖2　初載曲線的示意圖 Fig.2 Schematic of initial loading curve

首先，通過實驗獲得被描述對象的初載曲線(對壓電微動平臺而言，就是驅動電壓從零施加到壓電執行器所能承受的最高驅動電壓這一過程的實測升程曲線)后，見圖2，將其用足夠多的閾值r來劃分，從而將其描述為分段線性函數，即：

(5)

(6)

由式(5)可知，用PI模型來擬合被描述對象的實測曲線時，擬合精度的高低取決于閾值的劃分及權重的大小。通常，將閾值區間劃分得很小，以使劃分后初載曲線的各段接近于直線，以保證所建遲滯模型的精度，但這就使得算子數過多，且其中多數是權重為零的無效算子。而由式(4)可知，隨著遲滯算子數的增大，求解PI遲滯模型的運算量也隨之增大，從而在控制時就會降低被控對象的響應速度。可見，如何合理劃分閾值即如何使閾值最優化是至關重要的。

由式(6)可知，用PI模型來擬合被描述對象的實測曲線時，初載曲線在各閾值點處的斜率是用該點處遲滯算子的權重和來表達的，可見遲滯算子在各閾值點處的權重和越接近于該點初載曲線的斜率，模型的精度就越高。這樣，就可在保證模型精度滿足要求并使其在整個閾值區間變化盡量均勻的情況下，根據權重和的大小來劃分閾值。本文便基于該思想來劃分閾值，具體如下：

(1)用多項式函數擬合實測初載曲線；

(2)求出多項式函數在各采樣點處的導數(即斜率，該斜率可認為遲滯算子在相應采樣點處的權重)以及所有斜率和；

(3)將斜率和分為n等分，其中n為算子個數；

(4)求取各等分斜率和(該斜率和可認為在各閾值區間遲滯算子的權重和)處所對應的閾值。

圖3　不同算子數下實測初載曲線與模型曲線的誤差 Fig.3 Error of measured initial loading curve and model curve under different number of operators

圖3給出了在0～75～0 V三角波驅動電壓作用時不同算子數下實測初載曲線(為提高模型精度，圖示實測值為10次平均)和模型曲線之間的誤差。由該圖可知，當算子數≥7后，模型誤差漸趨穩定，減小已不明顯，故本文選擇算子數為7。圖4給出了算子數為7時的模型曲線及誤差曲線。由該圖可知，當算子數為7時，在16.3 μm的最大實測位移下，模型曲線同實測曲線的最大擬合誤差為0.208 μm，且誤差曲線波動較均勻。表1給出了算子數為7時所建模型的閾值及權重。由該表可知，所建模型中不含權重為零的無效算子。

圖4　微動平臺位移的實測曲線與模型曲線 Fig.4 Measured curve and model curve of displacement of micro-positioning stage

iriwi100.150160213.7820.069841324.9300.025238435.064-0.057557544.9950.058218654.926-0.009704765.060-0.020715

1.1.2微動平臺前饋控制器設計

壓電微動平臺的前饋控制器通過對所建遲滯模型求逆來獲得。由式(4)可知，PI模型的逆模型為：

(7)

式中：

(8)

將求得的PI模型參數代入式(8)，便可求得逆模型參數，然后將逆模型參數代入式(7)，則可求得逆模型，即壓電微動平臺的前饋控制器。

1.2反饋控制器設計

鑒于PID結構簡單、參數易于整定、魯棒性強、技術成熟，本文采用PID對壓電微動平臺進行反饋控制。常規數字PID控制算法為[22]：

u(k)=

(9)

式中:k為采樣時刻，T為采樣周期，u(k)為k時刻PID控制器的輸出，e(k)、e(k-1)分別為k和k-1時刻的偏差。

由式(9)所給出的PID為絕對式PID，其輸出受所有歷史狀態的影響，計算過程占用內存量大、耗時長，不利于實時控制。為此，本文采用占用內存、便于實時控制的增量式PID。由式(9)可得，PID控制器在k-1時刻的輸出為：

(10)

用式(9)減式(10)，可得PID控制器的遞推公式即增量式PID為：

Δu(k)=u(k)-u(k-1)=

g0e(k)+g1e(k-1)+g2e(k-2)

(11)

對式(11)兩端同時進行z變換，可得增量式PID控制器的離散脈沖傳遞函數為：

(12)

作者所在實驗室在以往采用PID對壓電微動平臺進行控制時，很容易產生超調[23]。超調可被看作是一種干擾，而濾波是抑制干擾的有效手段。為此，本文在常規數字增量式PID中引入濾波器，于是式(12)可表示為：

(13)

式中:1-f1z-1為濾波器，f1為濾波器參數，0

在式(13)中，令：

G(z-1)=g0+g1z-1+g2z-2

F(z-1)=(1-z-1)(1-f1z-1)

于是，可得：

F(z-1)U(z)=G(z-1)E(z)

(14)

進一步可表示為：

F(z-1)u(k)=G(z-1)e(k)

(15)

而由e(k)=r(k)-y(k)，可得：

F(z-1)u(k)=G(z-1)[r(k)-y(k)]

(16)

式(16)便是考慮了抑制超調的壓電微動平臺PID控制規律。

1.3復合控制器設計

根據式(7)與式(16)，將前饋控制與PID反饋控制相結合的壓電微動平臺復合控制規律為：

(17)

圖5給出了上述復合控制規律的框圖。

圖5　壓電微動平臺PID反饋控制系統框圖 Fig.5 Block diagram of PID feedback control of piezoelectric micro-positional stage

2微動平臺定位控制的實驗驗證

2.1微動平臺運動原理

圖6(a)給出了本文所設計的x、y兩自由度微動平臺的實物照片，其動平臺與臺體之間通過能夠發生彈性變形的圓弧形柔性薄板相連接，整個平臺有效工作臺面大、結構簡單緊湊、固有頻率高、集中應力小、便于傳感器集成。見圖6(b)，微動平臺運動的實現過程如下：在x方向壓電執行器驅動力Fx作用下，圓弧形柔性薄板發生彈性變形，使動平臺沿x方向產生微小位移，撤去Fx后動平臺在彈性恢復力作用下回到原始位置；y方向的運動過程與x方向相同。

圖6　微動平臺的運動原理 Fig.6 Motion principle of micro-positional stage

2.2復合控制實驗驗證

圖7為測量壓電微動平臺輸出位移的實驗系統。它由計算機、包含A/D和D/A轉換器的多功能數據卡、驅動電源、壓電執行器、微動平臺和電渦流位移傳感器構成，其工作過程如下：計算機生成一定的數據波形，經D/A轉換器輸出到壓電執行器驅動電源，驅動電源的輸出電壓作用于壓電執行器，驅動微動平臺產生微位移，該位移由電渦流位移傳感器測得，經A/D轉換器輸出到計算機。

圖7　微動平臺位移特試系統 Fig.7 System for measuring displacement of micro-positioning stage

由于微動平臺在x和y方向結構完全相同，故下面僅給出一個方向的控制結果。

2.2.1階躍響應

圖8為5 μm階躍輸入作用下無控制及經前饋、PID反饋、復合控制后壓電微動平臺的響應。由圖7(a)可知，無控制及經前饋、PID反饋、復合控制后壓電微動平臺達到5 μm目標值的響應時間分別為0.014 s、0.022 s、0.286 s、0.173 s；另外，PID反饋與復合控制均無超調，這表明所設計的PID控制器能夠抑制超調。由圖8(b)可知，在穩態情況下，無控制的穩態誤差最大，誤差中線近似為從0.5 μm到0.6 μm的上升直線(之所以上升，是由壓電執行器的蠕變特性所造成的)；前饋控制的穩態誤差較無控制明顯減小，誤差中線近似為從0.25 μm到0.4 μm的上升直線；PID反饋與復合控制的穩態誤差均較無控制及前饋控制顯著減小，若不考慮傳感器噪聲，它們的穩態誤差幾乎為零。可見，所設計的復合控制器既可使壓電微動平臺具有較快的響應速度，響應時間為0.173 s，又可提高其定位精度，穩態誤差幾乎為零。

圖8　不同控制下壓電微動平臺的階躍響應 Fig.8 Step responses of piezoelectric micro- positioning stage in different control

圖9　不同控制下壓電微動平臺的三角波跟蹤 Fig.9 Triangle wave track of piezoelectric micro- positioning stage in different control

2.2.2三角波跟蹤

圖9為變幅值三角波作用下經前饋、PID反饋、復合控制后壓電微動平臺的響應。由該圖可知，在最大位移為17.155 μm的變幅值三角波作用下，前饋控制的誤差中線在-0.6 μm～0.2 μm之間變化，而PID反饋與復合控制的誤差中線則幾乎為零線。這表明即使對三角波輸入，所設計的復合控制器也能使微動平臺的穩態誤差幾乎為零。而根據圖8(a)的結果可知，復合控制的響應時間比PID反饋快，這進一步表明設計的復合控制器可使微動平臺具有良好的定位效果，即定位時間快、定位精度高。

2.2.3任意信號跟蹤

圖10為任意波形信號作用下經前饋、PID反饋、復合控制后壓電微動平臺的響應。由該圖可知，在最大位移為16.430 μm的任意波形信號作用下，前饋控制的誤差中線在-1.15 μm～0.22 μm之間變化，而PID反饋與復合控制的誤差中線同樣幾乎為零線。這表明所提出的復合控制方法不僅對階躍信號、三角波信號等典型輸入信號具有很好的跟蹤效果，即使對任意輸入信號，也具有良好的跟蹤效果。

圖10　不同控制下壓電微動平臺的任意信號的跟蹤 Fig. 10 Arbitrary signal of piezoelectric micro-positioning stage in different control

3結論

為使壓電微動平臺具有較快的定位速度及較高的定位精度，在對傳統PI模型改進的基礎上建立了壓電微動平臺遲滯模型，所建遲滯模型僅有7個算子，且均為有效算子，在16.3 μm的最大實測位移下，模型最大誤差為0.208 μm；設計了將前饋同PID反饋相結合的壓電微動平臺復合控制器，實驗驗證了其有效性，結果表明：在復合控制作用下，壓電微動平臺達到5 μm目標值的響應時間為0.173 s，雖慢于前饋控制，但明顯快于PID反饋控制；在最大位移為17.155 μm的參考輸入作用下，若不考慮傳感器噪聲，微動平臺的定位誤差幾乎為零。

參考文獻

[1]李慶祥, 王東生, 李玉和. 現代精密儀器設計[M]. 北京: 清華大學出版社, 2004.

[2]Ge P, Jouaneh M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators[J].Precision Engineering, 1997, 20(2): 99-111.

[3]魏燕定. 壓電驅動器的非線性模型及其精密定位控制研究[J]. 中國機械工程, 2004, 15(7): 565-568.

WEI Yan-ding. Study on non-linear model of piezoelectric actuator and accurate positioning control strategy[J]. China Mechanical Engineering, 2004, 15(7): 565-568.

[4]張新良, 譚永紅. 基于動態PREISACH算子的壓電陶瓷動態遲滯智能建模[J]. 系統仿真學報, 2009, 21(9): 2682-2686.

ZHANG Xin-liang, TAN Yong-hong.Intelligent modeling of rate-dependent hysteresis in piezoelectric actuators based on dynamic preisach operator[J]. Journal of System Simulation, 2009, 1(9): 682-2686.

[5]Liu L, Tan K K, Chen S, et al. Discrete composite control of piezoelectric actuators for high-speed and precision scanning[J]. Industrial Informatics, IEEE Transactions on, 2013,9(2): 859-868.

[6]Kuhnen K, J anocha H. Inverse feedforward controller for complex hysteretic nonlinearities in smart-material systems[J].Control and Intelligent Systems, 2001, 29: 74-83.

[7]Janocha H, Pesotski D, Kuhnen K. FPGA-based compensator of hysteretic actuator nonlinearities for highly dynamic applications[J].IEEE/ASME Transactions on Mechatronics, 2008, 13(1): 112-116.

[8]張棟, 張承進, 魏強,等. 壓電微動工作臺的動態遲滯模型[J]. 光學精密工程, 2009, 17(3): 549-556.

ZHANF Dong, ZHANG Cheng-jin, WEI Qiang,et al. Dynamic hysteresis model of piezopositioning stage[J]. Optics and Precision Engineering, 2009, 17(3): 549-556.

[9]Li Z, Aljanaideh O, Rakheja S, et al.. Compensation of play operator-based Prandtl-Ishlinskii hysteresis model using a stop operator with application to piezoelectric actuators[J]. International Journal of Advanced Mechatronic Systems, 2012, 4(1): 25-31.

[10]Jurgen M, Thonmas S, Norbert F.Model-based control for ultrasonic motors[J]. IEEE/ASME Transactions on Mechatronics, 2000, 5(2): 165-180.

[11]Chang T, Sun X M.Analysis and control of monolithic piezoelectric nano-actuator[J]. IEEE transactions on control systems technology, 2001, 9(1): 69-75.

[12]賈宏光, 吳一輝, 宣明, 等. 一種新的壓電驅動器非線性數學模型[J]. 中國機械工程, 2002, 13(11): 929-932.

JIA Hong-guang, WU Yi-hui,XUAN Ming, et al. A new non-linear mathematical model for a PID actuator[J]. China Mechanical Engineering, 2002, 13(11): 929-932.

[13]崔玉國, 孫寶元, 董維杰, 等. 基于坐標變換的壓電陶瓷執行器遲滯非線性模型研究[J]. 大連理工大學學報, 2004, 44(2): 249-254.

CUI Yu-guo, SUN Bao-yuan, DONG Wei-jie, et al. Study of coordinate transform model for hysteresis nonlinearity in piezoceramic actuator[J]. Journal of Dalian University of Technology, 2004, 44(2): 249-254.

[14]Lin C J, Chen S Y. Evolutionary algorithm based feedforward control for contouring of a biaxial piezo-actuated stage[J]. Mechatronics, 2009, 19(6): 829-839.

[15]Elfizy A T, Bone G M, Elbestawi M A. Design and control of a dual-stage feed drive [J]. International Journal of Machine Tools & Manufacture, 2005, 45(2): 153-165.

[16]Wen C M, Cheng M Y. Development of a recurrent fuzzy CMAC with adjustable input space quantization and self-tuning learning rate for control of a dual-axis piezoelectric actuated micromotion stage[J]. Industrial Electronics, IEEE Transactions on, 2013, 60(11): 5105-5115.

[17]魏強, 張玉林, 于欣蕾, 等. 掃描隧道顯微鏡微位移工作臺的神經網絡PID控制方法研究[J]. 光學精密工程, 2006, 14(3): 422- 427.

WEI Qiang, ZHANF Yu-lin, YU Xin-lei, et al.Study on neural network PID control for micro-displacement stage of Scanning Tunneling Microscope[J]. Optics and Precision Engineering, 2006, 14(3): 422-427.

[18]Seo T W, Kim H S, Kang D S, et al. Gain-scheduled robust control of a novel 3-DOF micro parallelpositioning platform via a dual stage servo system[J]. Mechatronics, 2008,18(9):495-505.

[19]張棟, 張承進, 魏強,等. 壓電工作臺的神經網絡建模與控制[J]. 光學精密工程, 2012, 20(3): 587-596.

ZHANG Dong,ZHAND Cheng-jin, WEI Qiang, et al. Modeling and control of piezo-stage using neural networks[J]. Optics and Precision Engineering, 2012, 20(3): 587-596.

[20]陳遠晟, 裘進浩, 季宏麗, 等. 壓電式二維微動工作臺的遲滯補償與解耦控制[J]. 納米技術與精密工程, 2013, 11(3): 252-260.

CHNE Yuan-chen, QIU Jin-hao, JI Hong-li,et al. Hysteresis compensation and decoupling control of piezoelectrically driven two-dimensional micro-positioning stage[J]. Nanotechnology and Precision Engineering, 2013, 11(3): 252-260.

[21]姜晶, 鄧宗全, 岳洪浩, 等. 基于光控壓電混合驅動懸臂梁獨立模態控制[J]. 振動與沖擊, 2015, 34(7): 64-70.

JIANG Jing, DENG Zong-quan, YUE Hong-hao, et al. Independent modal control on cantilever beam based on hybrid photovoltaic/piezoelectric actuation mechanism[J]. Journal of Vibration and Shock,2015,34(7):64-70.

[22]陶永華, 尹怡欣, 葛蘆生. 新型PID控制及其應用[M]. 北京: 機械工業出版社, 1998.

[23]李勇. 二維并聯壓電微動平臺的控制方法研究[D]. 寧波：寧波大學, 2012.