用玻爾茲曼因子方程對“臨界點 沸點 熔點”特性進行數值計算

用玻爾茲曼因子方程對“臨界點沸點 熔點”特性進行數值計算

吳義彬

(南昌市老科學技術工作者協會江西 南昌330003)

摘 要：應用氣體、液體與冰的玻爾茲曼因子方程, 對自然界物質在“臨界點、沸點、熔點”時的物理特性進行數值計算,結果與觀測值高度吻合.事實證明,簡明的數學語言可以在很寬的溫度范圍內準確描述自然界物質物態變化的客觀規律;玻爾茲曼因子方程是更具普適性的物態方程.

關鍵詞：玻爾茲曼因子方程臨界點沸點熔點物理特性

收稿日期：(2014-08-31)

1引言

“熱力學的統計理論基礎的發展是19世紀物理學的卓絕成就之一.雖然，這個發展的許多觀念都源出于麥克斯韋和玻爾茲曼，但正是吉布斯的工作更直接地影響著我們現代對平衡態統計力學的表述”[1]; “在統計物理學中，物態方程可以根據系統內微觀粒子的屬性采用吉布斯的系綜方法獲得.然而，從單個粒子屬性到理論上計算出系統的宏觀量并不是一個很簡單的問題，需要根據粒子的特性建立統計模型，求出系統平衡時處在各微觀態的概率分布函數，然后由分布函數計算出各微觀量的統計平均，即宏觀量.在利用分布函數求統計平均時往往還需要利用各種近似算法.”[2]要在定量上得到精確的計算結果,更加“不是一個很簡單的問題”！

與“系綜方法”不同，直接從玻爾茲曼分布出發，在平衡體系邊界區域的表面保守力場中應用玻爾茲曼分布，導出分別描述氣體與液體的玻爾茲曼因子方程，不僅可以對液體的相變潛熱[3]、表面張力系數及其溫度變化率[4]等在定量上進行準確的數值計算，而且也可以對自然界物質在“臨界點、沸點、熔點”時的物理特性進行準確的數值計算.

2臨界點特性——氣體臨界系數存在趨同的特性

在臨界點上，由于液體的摩爾體積Vim與飽和蒸汽的摩爾體積Vqm相同,等于氣體的臨界摩爾體積Vgmc,故描述摩爾氣體的玻爾茲曼因子方程[5]變為

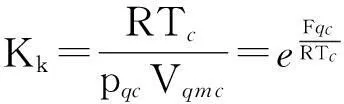
(1)

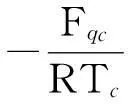
3臨界點特性——液體表面張力系數都等于零

從飽和蒸汽壓下單元液體玻爾茲曼因子方程出發,推導出了描述液體表面張力系數的數學公式[4]

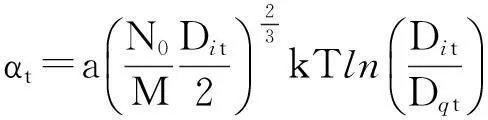
(2)

式(2)表明, 液體表面張力系數αt是溫度T,液體密度Dit與飽和蒸汽的密度Dqt的函數.由于臨界點上“液體及其飽和蒸汽間的一切差別都消失了”[7], 液體的密度與飽和蒸汽的密度相等, 即

由式(2)得液體表面張力系數αtc=0.

式(2)用精確的數學語言表明: 在臨界點上,液體的表面張力系數都等于零.與臨界點上“表面張力系數等于零[7]”的實驗觀測結果完全吻合．

4臨界點接近于0K物質的特性——液氦的表面張力極小

“氦原子間的相互作用(范氏力)和原子質量都很小，很難液化，更難凝固.富同位素4He的氣液相變曲線的臨界溫度和臨界壓強分別為5.20K和2.26大氣壓，1個大氣壓下的溫度為4.215K;溫度從臨界溫度下降至絕對零度時,液氦始終保持為液態，不會凝固.”

由于液氦僅僅在接近于零的0～5.20K溫度區間內存在, 液氣共存時的飽和蒸氣壓 ≤2.26大氣壓, 與液氦的臨界溫度、壓強相差無幾,“普通液氦的折射率和氣體差不多，因而不易看到它”; 所以液氦的密度Dit與其飽和蒸汽密度Dqt相差極小, 所以:

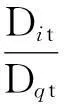
簡明的數學語言式(2),對定量計算液氦的表面張力系數也是正確有效的.

5沸點特性——沸點摩爾氣化熵大同小異 通常約為10R

5.1沸點摩爾氣化熵的數值計算

由飽和蒸汽壓下單元液體玻爾茲曼因子方程,可以導出沸點摩爾氣化熵的數學公式[3]

(3)

先應用式(3)定量計算液體沸點摩爾氣化熵(ΔS理沸),再與用沸點時氣化熱的實驗觀測值λ沸直接計算出來的沸點摩爾氣化熵(ΔS實沸)相對照，列于表1[3].

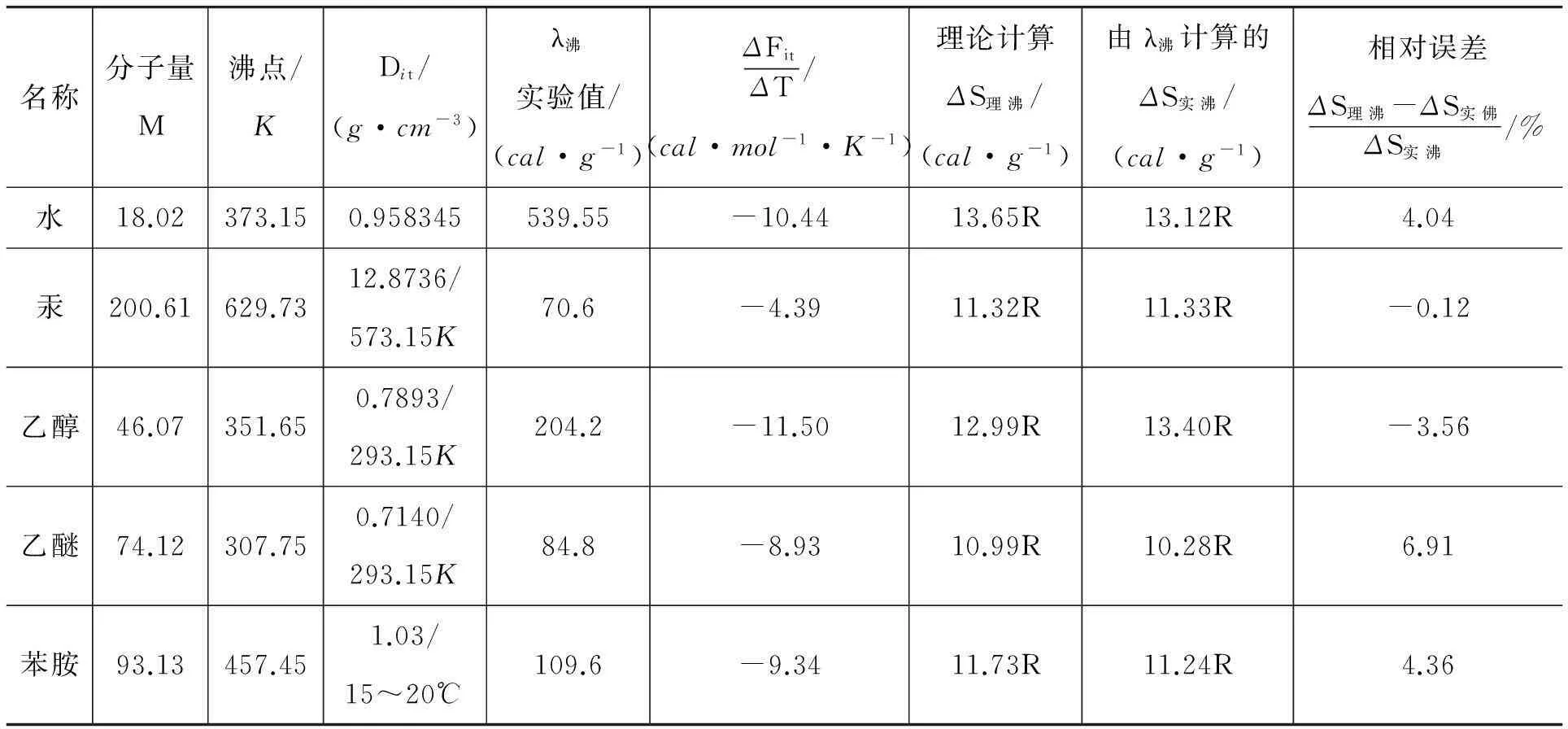
表1　純物質沸點摩爾氣化熵的理論計算

表注：ΔS理沸,ΔS實沸,可由表中數據直接代入下列兩式求出

表列數據表明：盡管水、汞、乙醇、乙醚、苯胺5種液體的物理性質迥異，沸點時的T,Dit,M等宏觀參量的數值相差很大，式(3)定量計算的結果ΔS理沸與實驗觀測值計算的結果ΔS實沸, 卻吻合得很好, 均近似為常量.

5.2驗證褚魯統規則

“褚魯統規則是一個有關液體的典型規則.它指出，在沸點下，一般液體的克分子蒸發熵大同小異，通常約為10R.”[8]

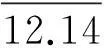
褚魯統規則不僅僅只是描述沸點物理特性的經驗規則，同時也可以是由式(3),在理論上準確計算論證的物理定律.

6熔點——冰升華熱與熔解熱的數值計算

6.1冰升華熱的數學公式

將飽和蒸汽壓下單元液體的玻爾茲曼因子方程[4]直接改寫為描述冰與飽和蒸汽平衡體系的玻爾茲曼因子方程

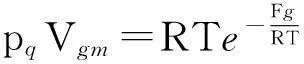
(4)

其中pq為冰的飽和蒸汽壓; Vgm為冰的摩爾體積;Fg為冰的摩爾表面自由能，數值上等于摩爾分子穿越冰與飽和蒸汽界面升華為蒸汽分子過程中,克服冰表面的保守力作用所做的功.

由式(4)可直接導出冰與飽和蒸汽界面的表面特性函數：

(1)摩爾表面自由能方程

Fg=RT(lnR+lnT-lnpq-lnVgm)

(5)

(2)摩爾表面熵方程

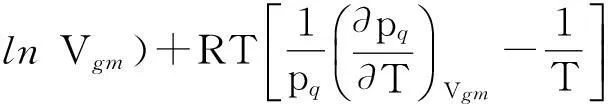
(6)

(3)摩爾表面能方程

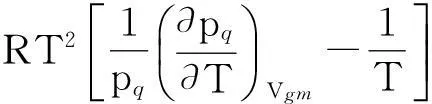
(7)

(4)摩爾升華焓方程

Hg=ug+pq(Vqm-Vgm)=

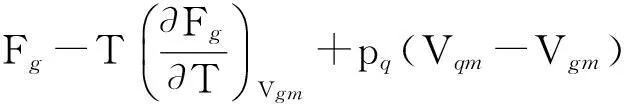
(8)

式(5)～(8)在可實驗實測的宏觀特性參量pq,Vqm,Vgm,T與不可實驗實測的液體表面特性函數Fg,Sg,ug,Hg之間架起了銜接的橋梁；為定量計算表面熱力學函數及其相關的物理量打開了方便之門.例如,從摩爾升華焓方程式(8)出發即可得到升華熱的數學表達式

(9)

6.2冰升華熱的數值計算

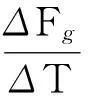
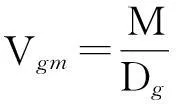
(10)

由物理手冊查得溫度為-2℃與0℃冰的實驗觀測數據[9]為

pq-2=3.879mmHg

pq0= 4.579mmHg

Dg-2≈ Dg0= 0.9g/cm3

將上列觀測數據代入式(10) 計算,即可得到

Fg-2=

1.985 9×271.15 =6 618.44cal/mol

1.9859×273.15 =6581.25cal/mol

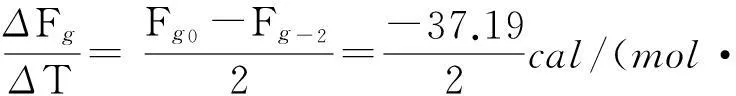
-18.595cal/(mol·℃)

(2) 理論計算升華熱λg0

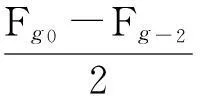
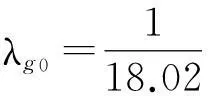
273.15×1.9859)cal/g=677.19cal/g

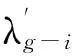
79.72cal/g+597.40cal/g=677.12cal/g

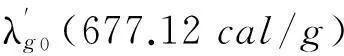
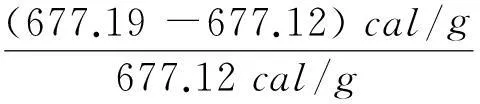
6.3冰熔解熱的數值計算

參考文獻由[3]表1查得:0 ℃時水氣化熱的純理論計算值為λi-q(599.96 cal/g)[3]. 可以用0 ℃時冰升華熱的純理論計算值λg0與0 ℃時水氣化熱的純理論計算值λi-q的差來計算0 ℃時冰熔解熱的純理論計算值λg-i,即

λg-i=λg0-λi-q=

677.19cal/g-599.96cal/g=77.23cal/g

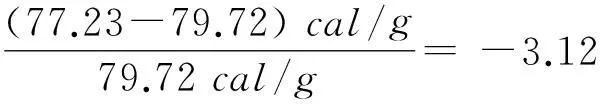
應用冰與飽和蒸汽平衡體系的玻爾茲曼因子方程式(4), 不僅可以對冰的升華熱與熔解熱進行純理論的數值計算, 而且計算結果與實驗觀測值都吻合得很好.

7結論

應用氣體、液體與冰的玻爾茲曼因子方程, 對自然界物質在“臨界點、沸點、熔點”時的物理特性進行數值計算,理論計算結果與實驗觀測值高度吻合.事實表明:

(1)簡明的數學語言可以在很寬的溫度范圍內準確描述自然界物質物態變化的客觀規律;

(2)玻爾茲曼因子方程是更具普適性的物態方程.

參 考 文 獻

1楊振寧.相變與臨界現象的引論性評注.戴定國譯.低溫與超導,1985(1):76

2湯文輝,張若棋.物態方程理論及計算概論(第2版).北京:高等教育出版社,2008. 13

3吳義彬.汽化熱與沸點汽化熵的理論計算.物理通報,2013(7):90

4吳義彬．飽和蒸汽壓下單元液體的物態方程及其應用.江西科學,2010,28(5):593

5吳義彬．實際氣體的玻爾茲曼因子方程.江西科學,2011,29(1):11

6(美)卡爾L·約斯.MATHESON氣體數據手冊(第1版).陶鵬萬，黃建彬，朱大方譯.北京：化學工業出版社，2003

7錢尚武，章立源，李椿. 熱學(第2版).北京：高等教育出版社，2008.272

8唐有祺. 統計力學及其在物理化學中的應用.北京：科學出版社，1979. 474

9(前蘇) К·П·雅闊夫列夫主編.簡明物理技術手冊第一卷.黃鏡權,尤烈之譯 .北京：中國工業出版社,1966.446,389

10王竹溪.熱力學(第2版).北京: 北京大學出版社,2005. 161

TheNumericalCalculationofCharacteristicsof

CriticalPoint,BoilingPointandMeltingPoint

ApplyingBoltzmannFactorEquation

WuYibin

(NanchangSeniorScientistsandTechnologistsAssociation,Nanchang,Jiangxi330003)

Abstract:By applying Boltzmann factor equation of gas, liquid, and ice, the physical characteristics of “critical point, boiling point, and melting point” of nature matter were numerically calculated and the results were highly consistent with the observed values. It is proved that the concise mathematical language is capable of describing the objective rules of change of nature matters or state within a wide temperature range. The Boltzmann factor equation is the state equation that has more universality.

Keywords:Boltzmannfactorequation;criticalpoint;boilingpoint;meltingpoint;physicalcharacteristics