力學中一個趣味問題的討論

力學中一個趣味問題的討論

楊星宇

(北京師范大學物理學系北京100875)

摘 要：在3維空間和n維空間中，當一個質點受到某一確定質量和密度物體的最大引力時，對該連續分布物體的形狀進行物理分析和數學運算可發現，當物體對質點有最大引力時，物體表面任意質量元對質點的引力在引力合力方向上的分量都相等，而且在3維空間中物體的形狀并非球形.

關鍵詞：萬有引力定律n維空間最值問題物體形狀

收稿日期：(2015-02-25)

對于3維空間中一個連續分布的物體，在質量和密度都保持不變的情況下，它具有什么樣的形狀時才會對一個質點產生最大的引力呢？會是球形嗎？對于n維空間中的物體情況又如何呢？下面分別進行討論.

1對3維空間中物體形狀的討論

1.1質點受力最大時 對物體形狀定性討論

若以質點所在位置為原點，質點所受引力合力的方向為極軸方向(即極角θ=0),建立球坐標系(r,θ,φ),其中r∈[0,+∞)，θ∈[0,π]，φ∈[0,2π)，則物體上的任意一點可由坐標(r,θ,φ)確定，物體表面可由函數r=R(θ,φ)描述.

要使質點的受力最大，物體的形狀應具有以下特性：

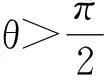
(2)物體形狀具有旋轉對稱性，繞極軸旋轉任意角度對稱，故物體表面函數簡化為r=R(θ)

“對稱性原理”[1]:原因中的對稱性必反映在結果中，即結果中的對稱性至少有原因中的對稱性那樣多.由牛頓第三定律可知，物體對質點有最大引力時，質點對物體也有最大引力.現在考慮質點對物體的引力，由萬有引力定律可知，質點產生的引力場以質點為球心成球對稱分布.不妨設物體為流體，物體受質點引力場作用，考慮到特性1的要求，當其受力最大時，可知物體形狀具有繞合力方向(即極軸方向)的旋轉對稱性.

1.2質點受力最大時 對物體形狀定量計算

設該連續分布的物體質量為M,密度為ρ且都保持不變，質點的質量為m.

在球坐標系中，物體體積和質點所受引力合力的大小分別為

令

R1(cosθ)=R(θ)t=cosθ

可得

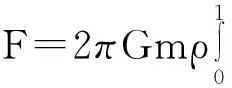
由變分法[2]，解得

即

畫出函數圖像如圖1所示，該曲線不是半圓.

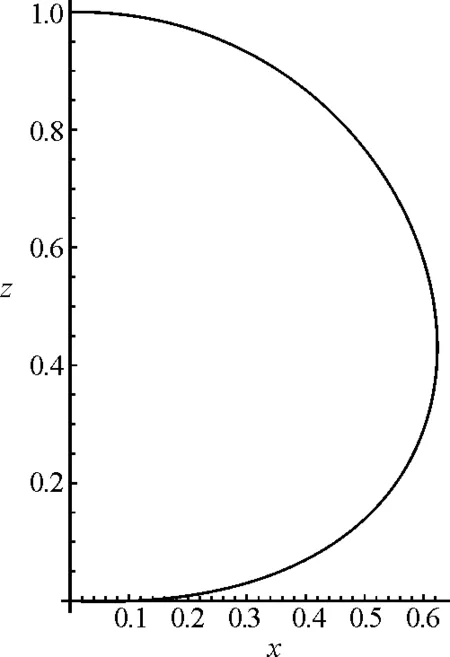
圖1

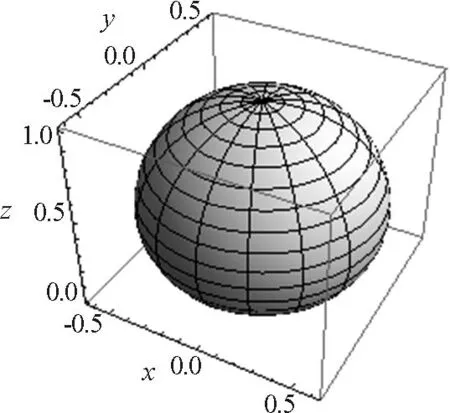
圖2

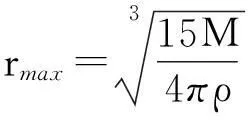
由對稱性可知，引力合力方向沿極軸正方向.

2對n維空間中物體形狀的討論

2.1質點受力最大時 對物體形狀定性討論

以質點所在位置為原點，質點所受引力合力的方向為θ1=0所在軸(可稱其為主軸)的正方向，建立n維超球坐標系[3](r,θ1,θ2,…,θn-2,φ),其中r∈[0,+∞),θi∈[0,π],φ∈[0,2π)，故物體上任意一點可由n維坐標(r,θ1,θ2,…,θn-2,φ)確定，物體表面由函數r=R(θ1,θ2,…,θn-2,φ)描述.

與前文分析論述同理可得，要使質點的受力最大，物體的形狀應具有以下特性：

(2)物體形狀具有旋轉對稱性，繞主軸旋轉任意角度對稱，故物體表面函數簡化為r=R(θ1).

2.2質點受力最大時 對物體形狀定量計算

將萬有引力公式推廣到n維空間

設該連續分布的物體質量為M,密度為ρ,且都保持不變，質點的質量為m.

在n維超球坐標系中，物體體積和質點所受引力合力的大小分別為

其中dRnV為n維超球坐標系中的體積元

dRnV=rn-1sinn-2(θ1)sinn-3(θ2)…

sin(θn-2)drdθ1dθ2…dθn-2dφ

令

R1(cosθ1)=R(θ1)t=cosθ1

sin(θn-2)dθ2…dθn-2dφ

可得

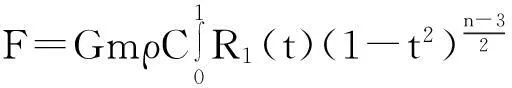
由變分法[2]，解得

即

其中

此時，物體對質點有最大的引力.

3結論

3.1在3維空間中的結論

在3維空間中，物體對質點有最大引力時，物體表面在球坐標系中的函數表達式滿足如下關系

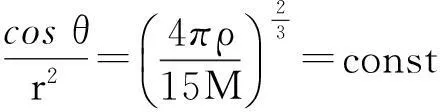
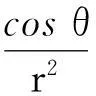
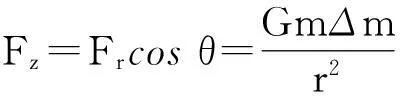
為常量，這表明，當物體對質點有最大引力時，物體表面任意質量元Δm對質點m的引力Fr在引力合力方向上的分量Fz都相等.

3.2在n維空間中的結論

在n維空間中，物體對質點有最大引力時，物體表面在n維超球坐標系中的函數表達式滿足如下關系

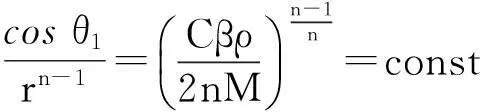
由上式可發現，當物體對質點有最大引力時，物體表面任意質量元對質點的引力在引力合力方向上的分量都相等.

3.3在2維空間中的結論

如果從n維空間退化到2維空間，那么當物體對質點有最大引力時，物體“表面”在平面極坐標系中的表達式滿足如下關系

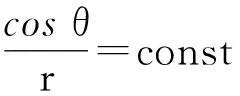
容易發現，上式就是極坐標系中圓的表達式.

故若物體是2維物體，物體對質點有最大引力時，物體的形狀是“球形”，不過此球形是2維空間的球形，即圓.

參 考 文 獻

1趙凱華.定性與半定量物理學.北京：高等教育出版社，1991.33

2歐斐君.變分法及其應用：物理、力學、工程中的經典建模.北京：高等教育出版社，2013.47～65

3StewartJ.Calculus:ConceptsandContexts[M].3rded.BROOKSCOLEPublishingCompany，2006:881

DiscussiononanInterestingMechanicalQuestion

YangXingyu

(DepartmentofPhysics,BeijingNormalUniversity,Beijing100875)

Abstract:Through physical analysis and mathematical operations on the shape of a continuous distribution object with constant mass and density in three-dimensional space and n-dimensional space respectively, find a conclusion: when the resultant gravity of the object on a given particle is maximal, the component of gravity on the given particle of any particle with euqal mass in the object′s surface in the direction of the resultant gravity is equal, and the shape of the object is not sphericity in three-dimensional space.

Keywords:thelawofuniversalgravitation;n-dimensionalspace;maximumorminimumproblem;objectshape