基于MAZAK 柔性制造線的粒子群與免疫算法研究?

張 利，孟祥凱，劉文生

（武漢輕工大學 機械工程學院，湖北 武漢 430023）

1 車間調度優化問題的描述

車間調度優化問題可描述為：有n個工件在m臺機器上加工，在已有的工序要求下，在工件的加工順序及時間給定的條件下，將n個工件在機器上排序，使得生產周期與加工時間最短、最優［1］。

由于日本MAZAK柔性制造生產線在現代制造業中得到了較廣泛的應用，因此本文將智能算法中的克隆免疫遺傳算法和粒子群算法運用在生產調度中，以提高生產效率，且可得到比較直觀的仿真結果［2］。

2 免疫遺傳算法的優化過程

免疫算法所求解的問題即抗原，首先提取抗原中的特征信息——疫苗；然后對疫苗處理將其轉變為求解問題方案；再將這個方案轉變成免疫算子來具體操作，抗原所提取的疫苗有多個，可將其進行組合后再注射。在提取疫苗的過程中，通過接種疫苗來提高適應度，而免疫選擇則是為了防止種群退化。

2.1 免疫遺傳算法接種疫苗［3］

設種群c＝（m1，…，），則對c種群接種的疫苗就是按比例λ（0＜λ≤1）得到的qλ＝λq個個體的變異，qλ為總的種群數量，疫苗是特定的特征信息。

2.2 免疫遺傳算法免疫選擇

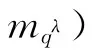
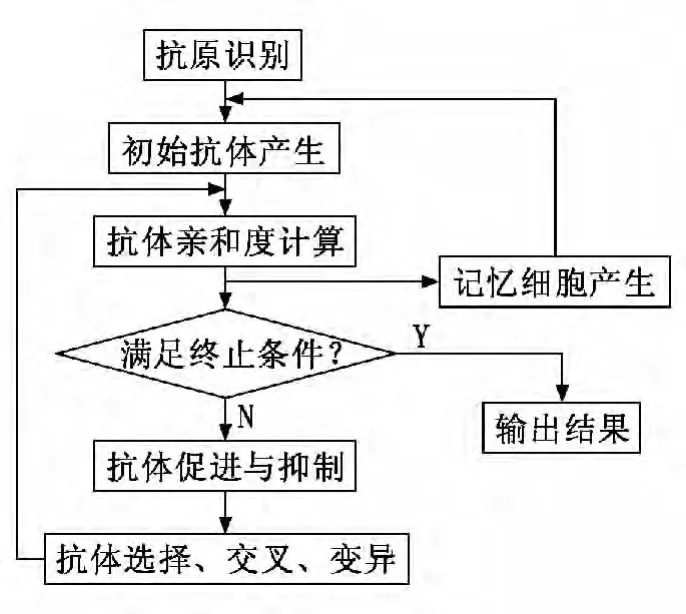
圖1 免疫遺傳算法基本流程

3 粒子群算法的優化過程

粒子群算法（Particle Swarm Optimization，PSO）是由美國的Kennedy博士和Eberhar博士于1995年提出的一種基于群智能的進化算法。在粒子群的優化算法當中，粒子在一個n維的空間上搜索時，每個粒子的位置是一個所要解答的問題的解，它持續地調整自己所處的位置來進行解的優化。本文中，第d維第i個粒子所處的位置用Xid來表示，用Pid表示粒子群中粒子搜索到的解，用Pgd表示所有的粒子所經歷的最好位置［5］，用表示粒子群的速度。因此，第d維的第i個粒子在某一時刻的速度為：

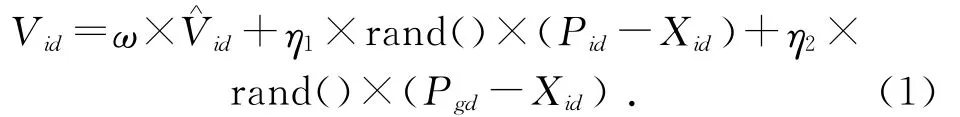
其中：ω為權重；η1，η2為粒子當中兩個解的參數值；rand（）為隨機生成的函數值。因此，由式（1）可以得到粒子群下一代的位置為：

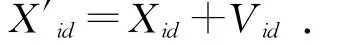
重新構造下一位置X′id的粒子速度V′id，其中粒子移動的算式為：

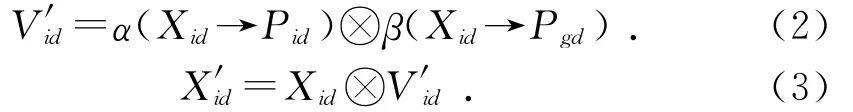
其中：α與β為隨機數，α，β∈［0，1］。交換序列（Xid→Pid）以概率α保留，基本的工序操作為α（Xid→Pid）；同樣地，交換序列（Xid→Pgd）以概率β保留，基本操作由β（Xid→Pgd）表示［6］。從式（2）、式（3）當中可以看出，它們是PSO算法求解的主要算子，并且在式子當中，α的值對局部最優移動的影響很大，當其增大時，粒子位置Pid也開始向最優解移動；同樣，β的值對局部的影響也很大，當其越大，對粒子位置Pgd的影響就越大。圖2為粒子群算法的調度過程。

4 實驗仿真與結果分析

本文采用經典的10/10/G/Cmax的Job shop調度問題，通過仿真得到求解結果，并確定是否是最優的結果。

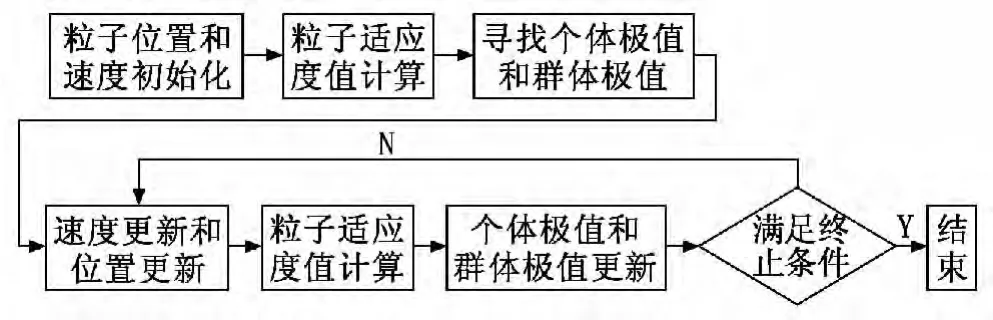
圖2 粒子群算法的調度過程

4.1 免疫遺傳算法仿真分析

克隆免疫遺傳算法繼承了遺傳算法的高度并行迭代模式［7］，采用原始克隆免疫算法的基本參數數據如下：初始抗體數為60，替換抗體為350，克隆選擇概率0.8，克隆細胞數80，迭代次數70。

在MATLAB 2013a下得到的免疫遺傳算法的調度仿真加工曲線為圖3～圖5所示。

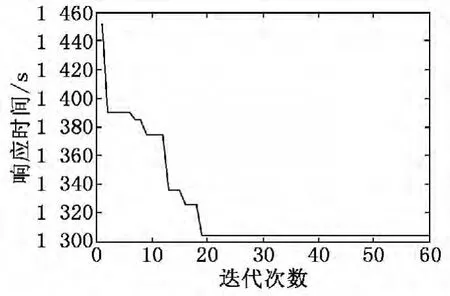
圖3 免疫遺傳算法最優完成時間變化曲線

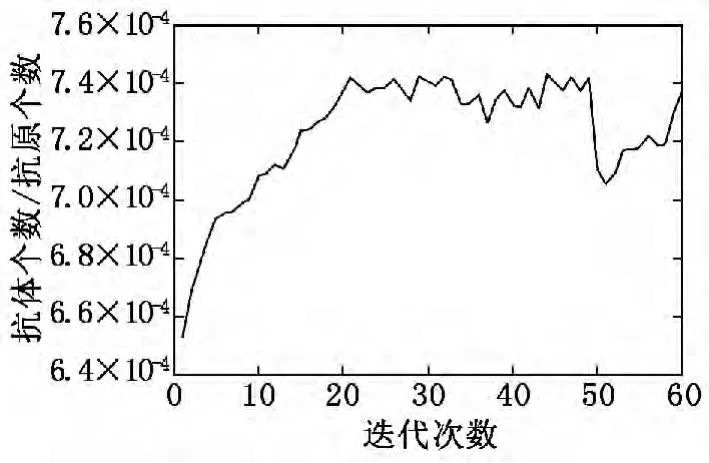
圖4 免疫遺傳算法親和度曲線

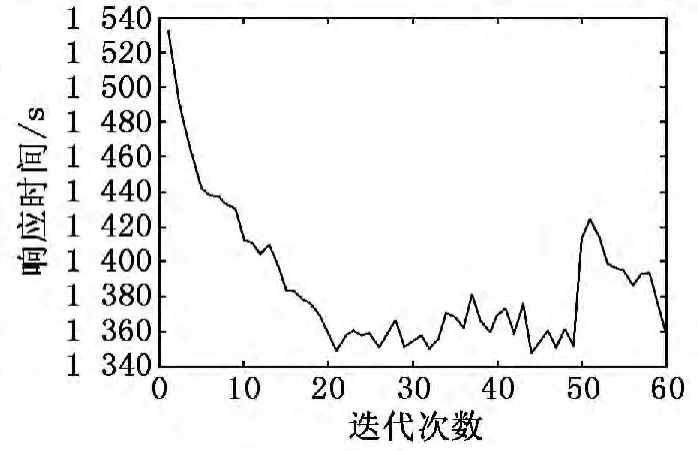
圖5 免疫遺傳算法加工時間曲線

圖3為免疫遺傳算法最優完成時間變化曲線，可以看到，在迭代過程中隨著迭代次數增加響應時間持續下降，最后恒定。圖4為免疫遺傳算法親和度曲線，親和度的變化不是恒定的，而是上下波動的。圖5為免疫遺傳算法加工時間曲線，它呈現與迭代次數有關的上下波動，其中迭代次數在20～40之間是最好的。

對10個工件、10臺機器進行作業調度，每個工件分別在10臺機器上各加工一次，由免疫遺傳算法得到的調度甘特圖見圖6。

圖6 免疫遺傳算法調度甘特圖

4.2 粒子群算法仿真分析

通過對10個工件、10臺機器進行作業調度，每個工件分別在10臺機器上各加工一次，每個工件的加工路線與每道工序對應的加工時間T與機器Js矩陣如下：

由粒子群算法得到的調度甘特圖如圖7所示。對比圖6與圖7可以看出，兩圖的調度順序完全不同，其中粒子群算法最優完成時間為1 128s，而免疫算法的調度最優完成時間為1 306s，遠遠地大于粒子群調度算法的最優調度時間。由此可以看出在柔性生產調度中粒子群算法優于免疫遺傳算法。

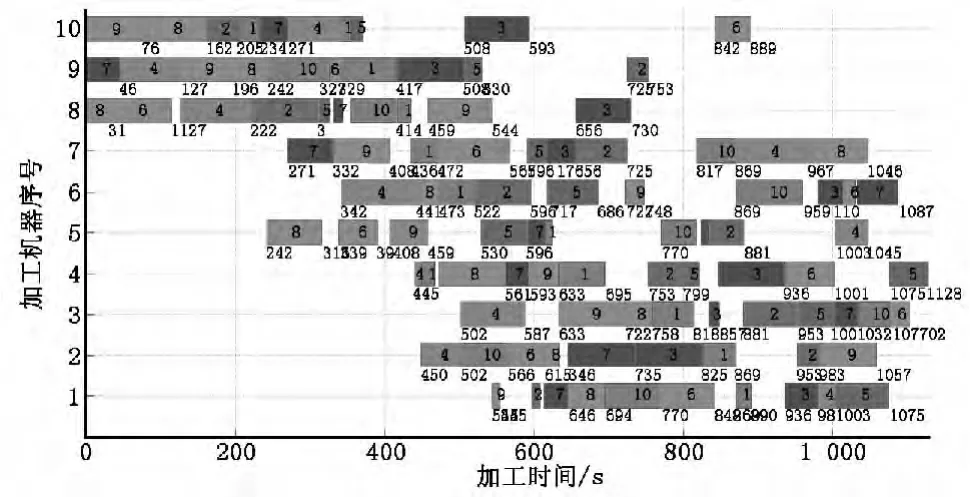
圖7 粒子群算法調度甘特圖

5 結束語

本文以日本MAZAK柔性生產線為基礎，通過對兩種算法的仿真比較分析，可以得到較為優秀的調度值。從兩種算法的對比中可以看到，粒子群算法要優于免疫遺傳算法調度，得到解的時間也相對較短。在今后的作業調度中，智能化調度將會得到更加廣泛的應用。

［1］于穎，李永生，樸孝春.粒子群算法在工程優化設計中的應用［J］.機械工程學報，2008，44（12）：226－231.

［2］宋曉宇，曹陽，孟秋宏.求解Job Shop調度問題的粒子群算法研究［J］.系統工程與電子技術，2008，30（12）：2398－2401.

［3］王凌.車間調度及其遺傳算法［M］.北京：清華大學出版社，2003.

［4］Rui Zhang，Shiji Song，Cheng Wu.A two－stage hybrid particle swarm optimization algorithm for the stochastic job shop scheduling problem ［J］. Knowledge－Based Systems，2012，27：393－406.

［5］李小華，熊禾根.基于粒子群算法的車間作業調度問題［J］.信息技術，2009（7）：19－21.

［6］何利，劉永賢，謝華龍.基于粒子群算法的車間調度與優化［J］.東北大學學報（自然科學版），2008，29（4）：555－568.

［7］Sha D Y，Lin Hsing－Hung.A multi objective PSO for job－shop scheduling problems［J］.Expert Systems with Applications，2009（6）：1065－1070.