航空器蒙皮維修圓補片小撓度彎曲力學分析?

董艇艦，陳 瑾，丁華鵬

（中國民航大學 工程技術訓練中心，天津 300300）

0 引言

半硬殼航空器是由桿件、桁條和隔框構成骨架，外覆蒙皮承受氣動載荷。由于航空器各部分受力情況復雜，不同區域維修方法各不相同，蒙皮維修是航空器結構修理的主要任務。目前基本按照SRM（Structure Repair Manual）結構修理手冊提供的通用計算公式設計蒙皮。經驗公式法依據受損材料的體積、遠超出極限強度的經驗假想強度和工作強度的比例關系，估測需要的加固點數，即鉚釘數，推測出補片的尺寸。經驗公式算法擴大了補片的結構尺寸，增加了維修工作量和成本，同時擴大了鉚接面積，顯然該方法不是精確的力學方案，而是采用大冗余度保證安全的簡化維修方案。該方法增加了維修工作量和成本，由于大面積的鉚接，還影響了機體的結構強度，特別是機體結構受限的尺寸空間，會導致普通維修無法進行，影響航空器運營［1］。本文運用廣義內力素分析方法［2］，通過精確力學［3］計算確定圓補片小撓度彎曲構型，量化制定補片的尺寸參數、工藝參數和力學參數，實現補片的數字化優化設計和制作。

1 廣義內力素薄板［4］模型

蒙皮維修的圓形補片面積一般較小，曲率很小，可看作平板［5］（此處限于小曲度區域）。本模型設定載荷垂直于板面，則補片為二維結構彈性板，可產生拉壓、剪切、彎曲和扭轉變形，按薄板殼理論建立的蒙皮補片單元模型如圖1、圖2所示。按照廣義內力素性質，在坐標系中設T1和T2為面內拉力，T12和T21為面內切力，Q1和Q2為橫剪力，均為中面單位長度上作用的力；M1和M2為彎矩，M12和M21為扭矩，均為中面單位長度上作用的力矩。

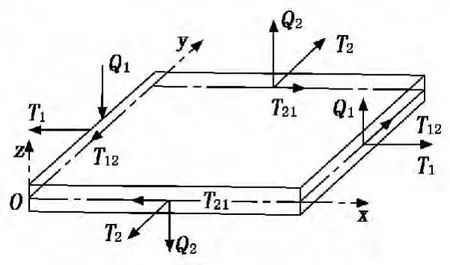
圖1 蒙皮補片單元受力模型

圖2 蒙皮補片單元受彎矩模型

設板厚為2h，當板橫面上作用平行于中面的正應力σ1，σ2和剪應力τ12時，力和力矩的表達式為：

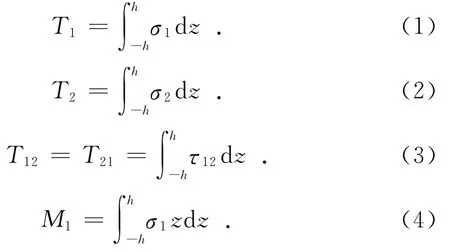
此外還有橫向剪應力τ1z和τ2z的合力：

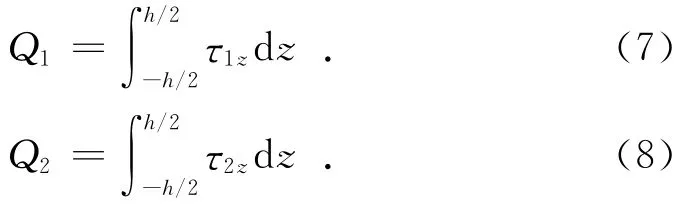
式（1）～式（8）通過面內拉力、剪力、彎矩和扭矩構成廣義內力素，精確表達了平板內所有力的分布情況。

2 補片小撓度彎曲微分方程及其解

當薄板受力發生彎曲時，沿x軸方向的位移u、沿y方向的位移v和撓度ω有下列幾何關系：

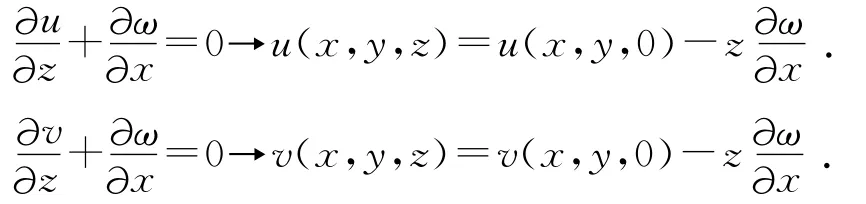
忽略中面變形，可得板的面內應力與板的法向位置的二階導數，即應變εx，εy，γxy：

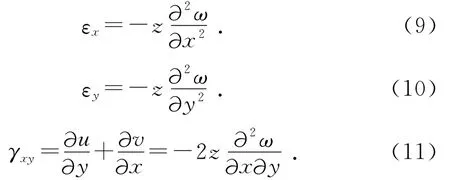
結合廣義胡克定律可知板小撓度彎曲的彈性關系（其正方向的定義見圖1、圖2）：

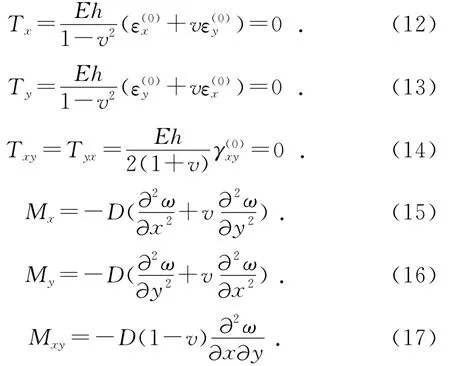
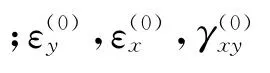
彎曲的平衡方程通過板微元體平衡獲得。已知圖2為邊長dx和dy，厚度為2h的板微元體［6］，板面法向載荷為p（x，y）。則由力矩平衡條件可得：

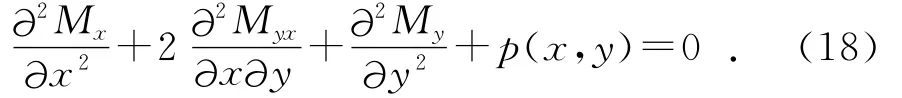
將式（15）～式（17）代入式（18）得：

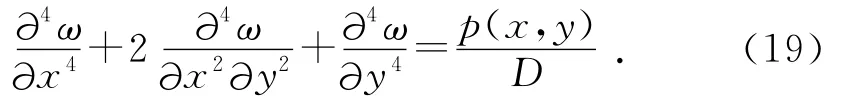
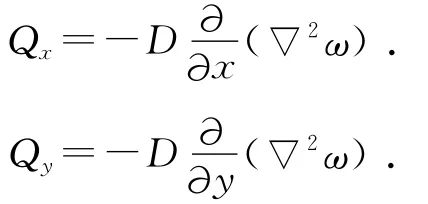
對于軸對稱載荷作用的圓板，在柱面坐標內x＝y＝r，則公式（19）變為：

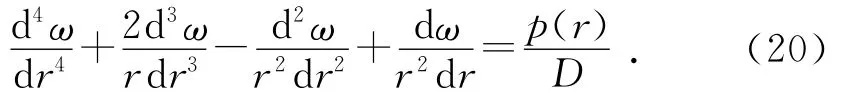
解式（20）可得：

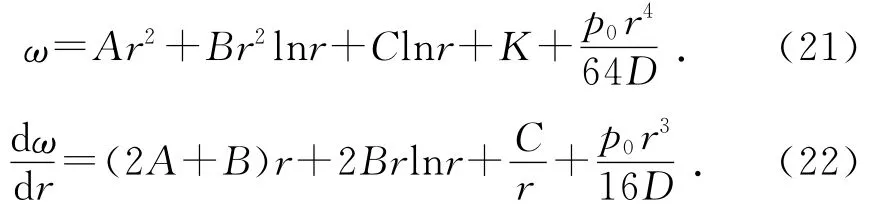
其中：A，B，C，K均為待定系數；p0為均布載荷。同理可以求得對應的彎矩Mr和Mθ，扭矩Mrθ，橫剪力Qr和Qθ：

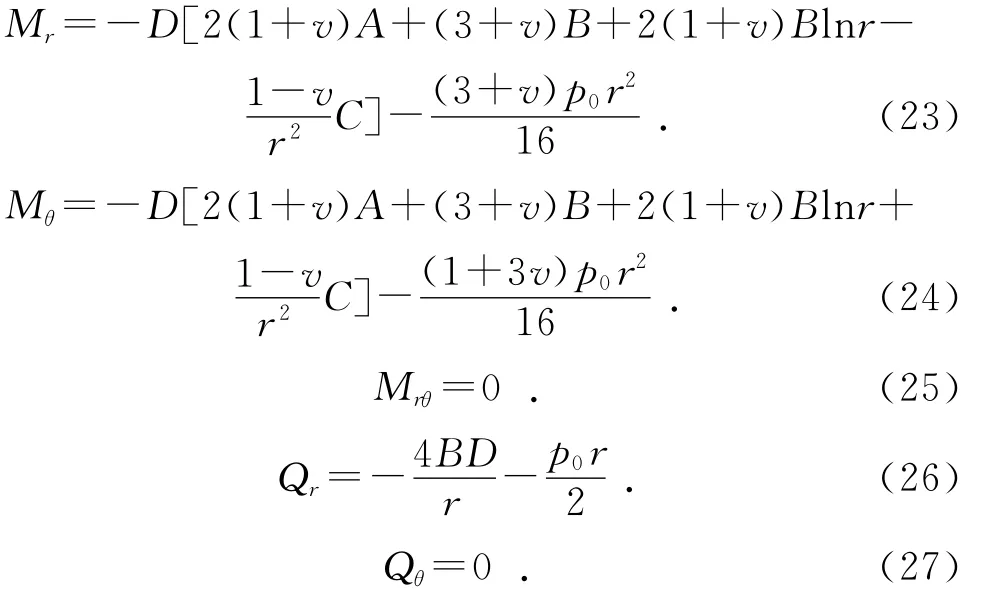
3 圓補片小撓度彎曲力學分析

針對蒙皮圓補片，周邊認定為簡支，受均布載荷p0作用，可以求得圓補片的撓度與應力。結合柱面坐標系下的邊界條件可得：

（1）r＝0時，ω有界，C＝0，無集中力作用，則B＝0。

（2）r＝R（R為補片半徑）時，ω＝0，Mr＝0，將其分別代入式（21）和式（23）得：AR2＋K＋p0r4/（64D）＝0，－2D（1＋v）A－（3＋v）p0R2/16＝0。

由此求得柱面坐標系下對應的撓度ω、彎矩與剪力：

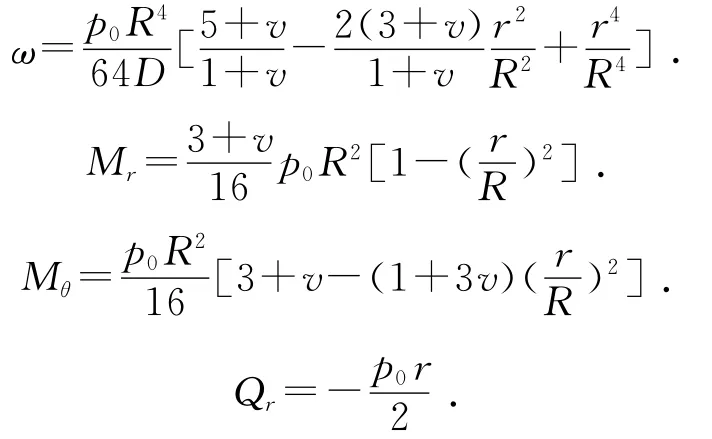
并可得板中應力：

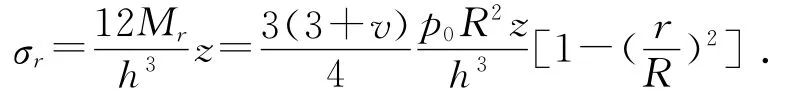
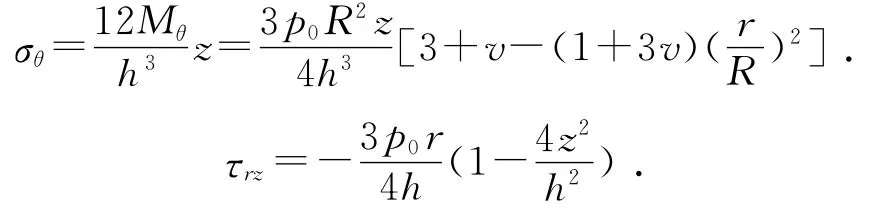
σr，σθ和τrz的分布狀況如圖3和圖4所示。

圖3 σr，σθ 的分布狀況

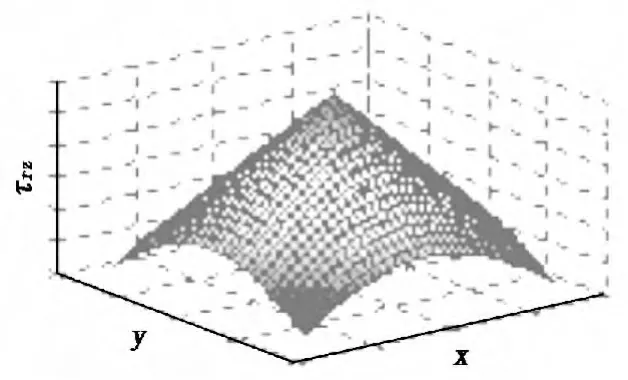
圖4 τrz的分布狀況

由圖3和圖4可知，圓補片的正應力和剪切力在中心處最大，正應力分布為球冠型，中心區域最大，近似拋物線分布；剪切力分布呈圓錐型，即線性增長。在中心處，即當r＝0時：

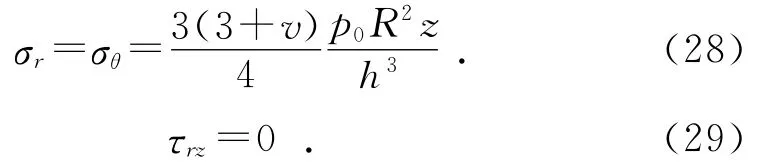
在邊緣處，即r＝R時：

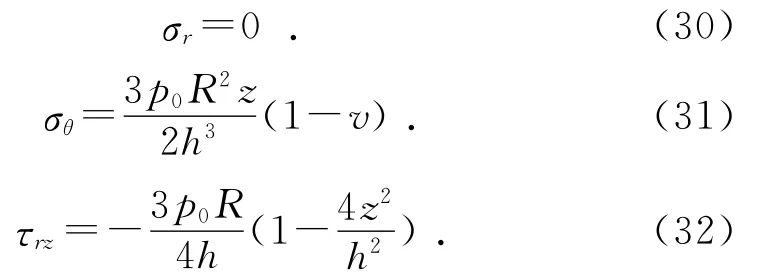
4 圓補片設計的優化方法［7］

傳統的維修中，補片尺寸是按照鉚釘5d間距和2d邊距（d為鉚釘直徑）排布規則推算的，一般情況余度很大，安全系數高，但工作量也大，維修成本高。

應用撓度力學分析方法，量化計算安全范圍內補片的精確尺寸，再通過邊距規則修正尺寸，即可最優化地得到補片的設計尺寸。由式（31）、式（32）可得到由正應力與切應力來確定的補片尺寸，即：

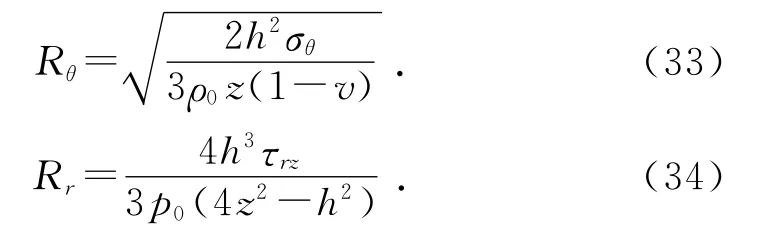
因此只須確定補片需要負荷的最大壓力和剪力，代入補片的結構參數，即可計算出2種補片的半徑尺寸，選擇最大的R值作為理論計算尺寸，按照邊距規則排列鉚釘，最外圈按照上限原則保證最大覆蓋取整方法即可完成工藝尺寸的制定。

該優化方案以力學基本理論為指導，量化地確定了航空器蒙皮孔型損傷維修中的補片尺寸，有效減少了維修成本，為航空器蒙皮維修指明了發展方向。但優化方案中具體參數的確定需要大量的實驗數據，該方案雖然得到了量化公式，但如果想要在實際應用中實現，還需要大量的可靠性驗證才行，這有待進一步的研究討論。

［1］任仁良.維修基本技能［M］.北京：清華大學出版社，2010.

［2］薛明德，向志海.飛行器結構力學基礎［M］.北京：清華大學出版社，2009.

［3］王敏中，王煒，吳際可.彈性力學教程［M］.修訂版.北京：北京大學出版社，2011.

［4］劉鴻文.材料力學［M］.北京：高等教育出版社，2011.

［5］崔延，屠鳳蓮.不規則形狀薄板的平面應力分析［J］.機械設計與制造，2012（8）：218－219.

［6］Xu B X，Wang M Z.The quasi eshelby property for rotational symmetrical inclusions of uniform eigencurvatures within an infini template［J］.Proc.Roy.Soc，2005，A461：2899－2910.

［7］J Cutle. Understanding Aircraft Structures ［M ］.Blackwell Publishing Ltd：Oxford，Malden，MA，2005.