非自治系統關于部分變元的強穩定性＊

劉 丹

（山東科技大學，山東 青島 266590）

1 引言與定義

Liapunov直接法是研究系統穩定性的一個強有力的方法，在一個系統中存在許多的變元，但往往一部分變元的性質我們掌握不了，或者不需要研究和證明。這就引出了強穩定性的概念，如文獻［1-3］提出了關于部分變元的強穩定性的概念，但關于部分變元的強穩定性的判定定理還不夠豐富。文中將文獻［4-8］中驗證部分變元穩定性方法改進，得到了一些關于部分變元的強穩定的判定定理。

考慮n維非自治系統

其中x∈Rn，f（t，x）∈C［I×Ω，Rn］，I=［0，+∞），Ω 為開區域，f（t，0）≡0。記

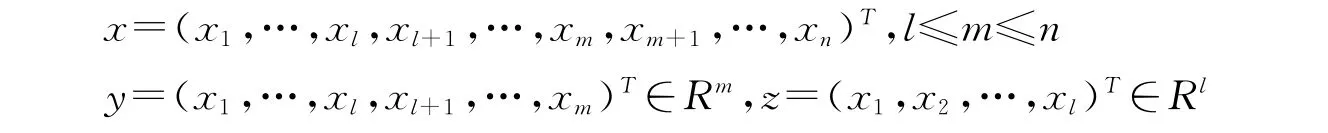
假設當Ω=｛x∶‖y‖≤H，‖z‖≤+∞｝時，（1）的解唯一且可延拓到I上。

定義1［1］稱（1）的平凡解關于部分變元z對y 強穩定，如果對于任何ε＞0和t0∈I，存在δ（ε，t0）＞0，使得當x0滿足‖y0‖≤δ（ε）時，對一切t≥t0，有‖z（t，t0，x0）‖≤ε。

定義2［1］稱（1）的平凡解關于部分變元z對y 強一致穩定，如果對于任何ε＞0，存在δ（ε）＞0，使得當x0滿足‖y0‖≤δ（ε，t0）時，對一切t0∈I，當t≥t0時有‖z（t，t0，x0）‖≤ε。

定義3［3］稱（1）的平凡解關于部分變元z對y 強吸引的，如果對于任意ε＞0及t0∈I，存在δ（t0）＞0，使得當x0滿足‖y0‖≤δ時，存在T（ε，t0，x0）＞0，當t≥t0+T（ε，t0，x0）時有‖z（t，t0，x0）‖≤ε，即z（t，t0，x0）=0。

定義4［3］稱（1）的平凡解關于部分變元z對y 強漸近穩定的，若（1）的平凡解關于部分變元z對y 是強穩定的且z對y 是強吸引的。

定義5［1］對于連續函數V（t，x）=V（t，y，z），若有V（t，0，z）≡0，則稱V（t，x）為推廣的Liapunov函數或y-V 函數。

2 判定定理

定理1 存在y-V 函數V（t，x）及連續函數列｛Un（t，x）｝滿足

（1）Un（t，x）≥a‖z‖，a∈K，Un（t，0）=0

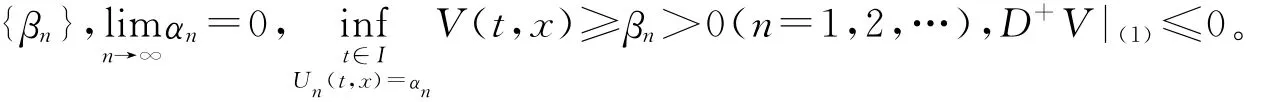
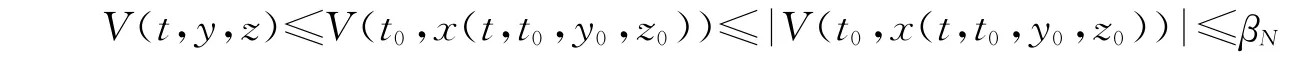
下面證明對一切t≥t0均有Un（t，x（t，t0，y0，z0））＜αN。

若Un（t，x（t，t0，y0，z0））＜αN不成立，故可找到t1≥t0，使得

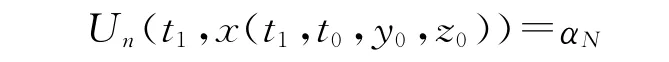
于是

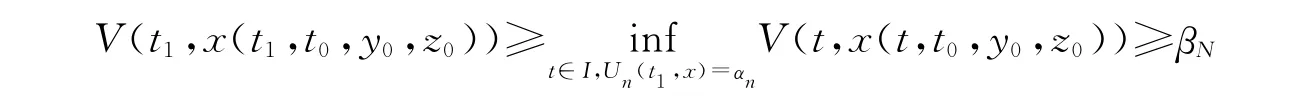
這與（6）式矛盾。從而

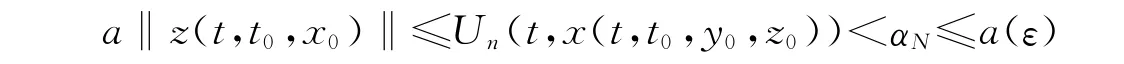
故對一切的t≥t0，有‖z（t，t0，x0）‖＜ε。則系統（1）的零解關于部分變元z對y 強穩定。

定理2 若存在y-V 函數V（t，x）滿足

（1）V（t，x）≥a（‖z‖）且｜V（t，x）｜≤b（‖z‖），其中a，b∈K。

（2）D+V（t，x）≤0。則系統（1）的零解關于部分變元z對y 強一致穩定。

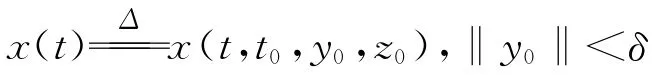
由（2）D+V（t，x）≤0，故

從而‖z（t，t0，x0）‖＜ε，則系統（1）的零解關于部分變元z對y 強穩定。

又因為｜V（t，x）｜≤b（‖z‖），取δ（ε）=b-1（a（ε））不依賴于t0，當‖y0‖＜δ有

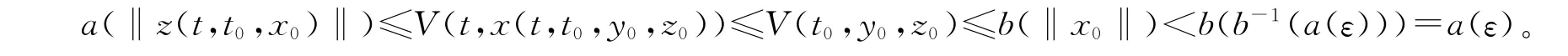
從而對一切t≥t0，有‖z（t，t0，x0）‖＜ε。故系統（1）的零解關于部分變元z對y 強一致穩定。

注：在定理2中去除｜V（t，x）｜≤b（‖z‖）條件后也是判定零解關于部分變元z 對y 強穩定的一個方法。

定理3 若存在y-V 函數V（t，x）滿足

（1）有正定函數w（z），使得V（t，x）≥θ（t，x）w（z），V（t，0）=0。

證明 由條件（1）知由于w（z）是正定函數，故存在φ∈K，使得w（z）≥φ（‖z‖），故

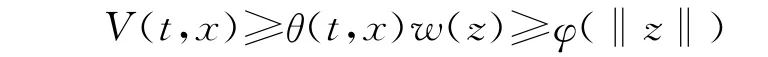
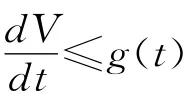
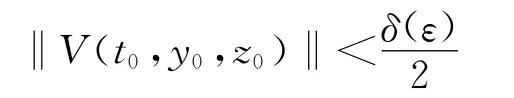
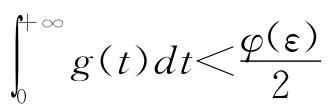
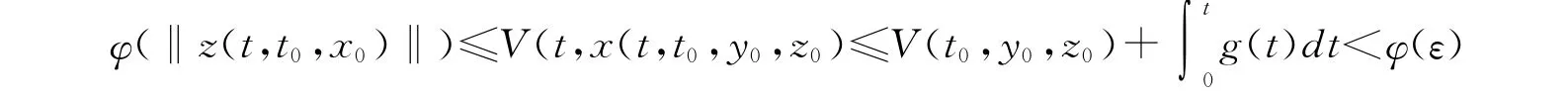
從而‖z（t，t0，x0）‖＜ε。即系統（1）零解關于部變元z對y 強穩定。

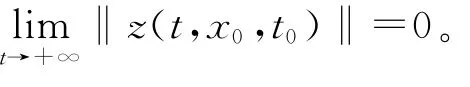
對任意的的ε1＞0，存在T（ε1，t0，x0）＞0，當t≥t0+T 時

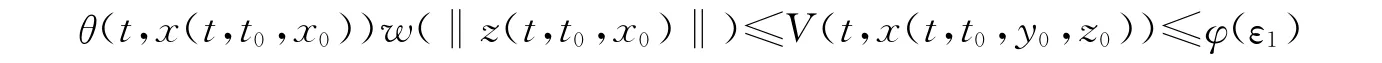
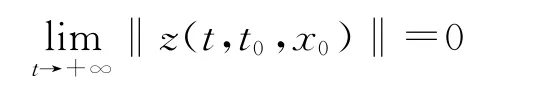
即系統（1）零解關于部分變元z對y 強吸引。

綜之，系統（1）零解關于部分變元z對y 強漸近穩定。

作者衷心感謝馮濱魯教授對本文的指導、審閱。

［1］周康.關于部分變元的強穩定性的基本定理［J］.華中師范大學學報：自然科學版，1995，29（1）：24-26.

［2］張維.微分系統關于部分變元的強穩定性［J］.華中師范大學學報：自然科學版，1992，26（4）：408-412.

［3］孟新柱.部分變元的強穩定性研究［J］.山東科技大學學報：自然科學版，2002，21（3）：18-20.

［4］廖曉昕.穩定性的數學理論與應用［M］.武漢：華中師范大學出版社，1988.

［5］馮濱魯.兩類非線性系統的不穩定性［J］.山東礦業學院學報，1992，11（2）：200-203.

［6］馮濱魯，王向榮，王朝陽.關于部分變元全局漸近穩定性的新判據［J］.山東礦業學院學報，1994，13（2）：191-195.

［7］么秉春，趙文凱.關于擾動方程的零解對部分變元的穩定性［J］.河北輕化工學院學報，1993，14（4）：29-34.

［8］舒仲周，謝建華.Liapunov穩定定理的一個注記［J］.西南交通大學學報，1988，23（2）：38-44.