電偶極子對電容參數影響分析
李 春
(上海航天技術基礎研究所,上海 201109)
0 引言
電容測試篩選發現老化后容量值與初測值相較有偏差,尤其是瓷介電容器老化篩選后放置一段時間容量仍有偏差,且部分有機介質電容的容量值偏差超過了標稱允許范圍,影響測試結果,其中多數出現容量變小,老化結束放置一段時間后,容量又有所恢復,恢復的程度和時間不同。破壞性物理試驗發現,這些電容的內電極無明顯異常。目前,國內各生產廠老化后測試均參照各類電容的國軍標執行,統一規定放電時間約24h,并未因材料區別而有其他特殊要求。
為此,本文對老練后電容解容量、損耗變化的原因進行了研究,討論了去老練應力時間。
1 電偶極子與電偶極矩
1.1 電偶極子
電容中充滿著電介質,每個電介質的分子中有正、負電荷。受外電場作用時,正、負電荷分別集中于一點,相隔一定距離,且電量相等,則該分子為電偶極子。根據電介質分子的結構可分為極性分子與非極性分子[1-4]。外電場場強越強,電偶極子產生的電矩就越大,微觀角度解釋如下[5-6]。
a)非極性分子主要有電子極化、原子極化兩種。電子極化是指在外電場中每個原子的價電子云相對原子核發生位移,原子極化是指在外電場中不同的原子核間發生相對位移。隨著外電場的場強增大,正、負電荷做的功增加,間距增加,電偶極矩增大。該極化亦稱為變形極化。
b)極性分子極性分子的正負電荷重心本不重合,自身帶固有偶極子,除變形極化外,還有取向極化。取向過程要克服本身慣性與旋轉阻力,隨著外電場的場強增大,取向極化更整齊,電偶極矩增大。分子熱運動使偶極子的取向趨于雜亂,故取向極化還與溫度有關。
1.2 外電場作用下受力
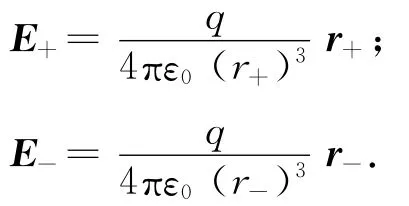
離偶極子很遠處,即r?|l|時,|r+|=|r-|≈r。此處:r為電子至點P的距離。則點P的總場強
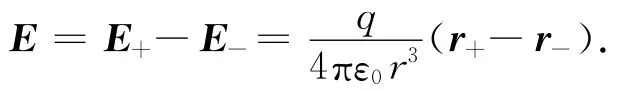
因r+—r-=-l,則
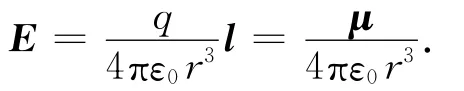
由上述分析可知:在電偶極子中垂線方向距離偶極子較遠處的場強與電偶極矩成正比,與電偶極矩方向相反。由總場強公式,根據矢量三角形可推導出非中垂線上的場強也有相同的表達式。
外場強E0增大,正負電荷距離增大,則E變大,μ也隨距離增大而增大,即隨E0變大。
因存在電偶極子及自身在外電場中受力作用,產生了與外場強方向相反的電場強度,整體上削弱了原外電場強度,這種削弱場強隨外電場場強增強而增強。
用電極化強度p表征總的單位體積內電偶極強度,有
橋梁模板是高速公路橋梁建設施工時用來固定橋梁的,同時也是施工中最重要的。在構架橋梁模板之前,首先需要計算機模擬技術構建出空間立體圖紙,根據圖紙進行模板拼接。模板構架材料一般采用可塑性較好的鋼材,每節模板高度約為1.5m。模板材料定形以后,為了保證模板拼接后的穩定性還需對模板材料進行二次加工,保證模板表面光滑、平整,同時也方便模板的拆裝。
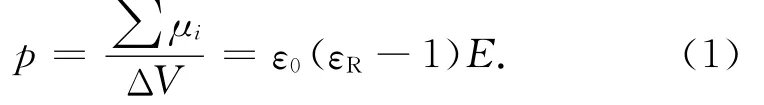
式中:ε0為真空介電常數;εR為相對介電常數;μi為每個電子產生的電矩;ΔV為單位體積;E為電場強度。
1.3 介電常數
兩塊平行放置的金屬板間為真空狀態,兩金屬板帶有+Q,-Q等量電荷,用電壓計測得電壓為V0。使平行板間充滿絕緣介質,保持兩平行板上電量不變,測得電壓為V,因V=V0/εR,則V變小,又因V=Ed,V0=E0d,故E=E0/εR。此處:d為兩極板間距離。
電偶極子的極化在金屬板上產生與金屬板極性相反的電荷,金屬板表面電荷減小,電荷密度也減小,表現為場強減小,電場強度為原來的1/εr,且可推導由極化產生的反向電荷密度與極化強度一致,即

極化中,變形極化主要取決于分子電子云的分布,故變形極化隨外電場強度而變,而取向極化則需克服本身慣性、旋轉阻力及分子熱運動,取向極化相對變形極化為時間的函數。變形極化產生的介電常數εC,取向極化產生的介電常數為εr。
2 容量變化
老化后,多層片式疊層電容的容量變化較常見,本文主要研究平行板結構的電容器。由高斯定律,電容容量

式中:S為極板面積。可見C與本身所帶電量Q和兩端電壓V無關,僅與電介質本身性質和S,d有關。
對極性分子的取向極化時,需克服分子本身的黏滯系數、分子間熱運動,可知極化和去極化過程與溫度和時間有關,故極化強度是關于場強、溫度和時間的函數,但式(3)并未體現,因此以電容本身定義式分析容量變化。
為便于分析容量變化趨勢,老化后立即測試,不考慮降溫及時間影響,變形極化完全緣由場強變化,而相同測試電壓產生的變形極化相同,產生的反向電荷密度測試前后無變化,僅考慮由取向極化產生電荷密度的變化。
設額定電壓100V,測試時電壓1V,老化時在溫度125℃加老化電壓200V。由式(1)、(2)可得
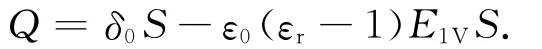
式中:δ0為無介質時極板上的電荷密度,且δ0=ε0ES。
將式(4)代入C=Q/V,則原始容量

老化 后 測 試 電 壓 不 變,但Q=δ0S—ε0(εr—1)E200VS,故

式中:E1V,E200V分別為1,200V 時的場強;C1為老化后容量。
因E200V>E1V,C1<C0,即容量變小,且C0=ε0εrS/d,與式(3)相同,滿足電容定義。
容量變小時,根據電容定義式,ε0,d,S為定量,比較兩式,老化后使εr變小。
3 損耗變化
3.1 極化過程
分析電介質在電場中的極化過程,平衡態的束縛電荷非瞬間產生,而是隨時間延長不斷增加,最后達到平衡態。交變電場中,極化過程應為電場變化頻率的函數。從極化機理上看,變形極化速率較快,跟得上電場變化,而取向極化需一定時間達到平衡,未必能跟上電場變化,因此將其分為兩部分:
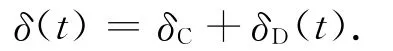
式中:δC為瞬時產生的電荷密度,且

δD為隨時間而產生的電荷密度,足夠長時間后電荷密度達到δDR。此處:εC為瞬時介電常數。有
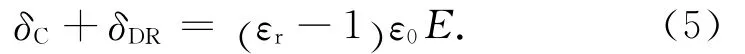
式中:εr為瞬時介電常數。由式(4)、(5)得
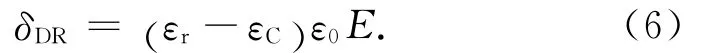
從動力學考慮,δD(t)變化到δDR速率與其偏離平衡態的程度成正比,則
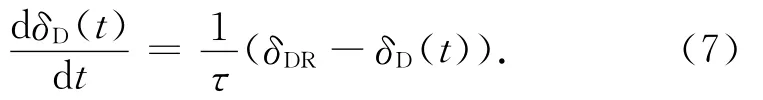
式中:1/τ為比例系數。
將式(6)代入式(7),整理后
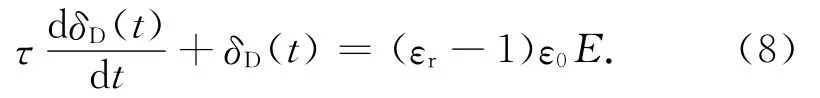
3.2 損耗變化
測試中使用頻率1kHz或1MHz、電壓1V的測試電壓,其場強亦是交變的,則E(?,t)=E0×exp(j?t)。此處:?為交流電壓的角頻率;j為虛數單位。此時,式(8)的微分方程中通解e-t/τ→0,則
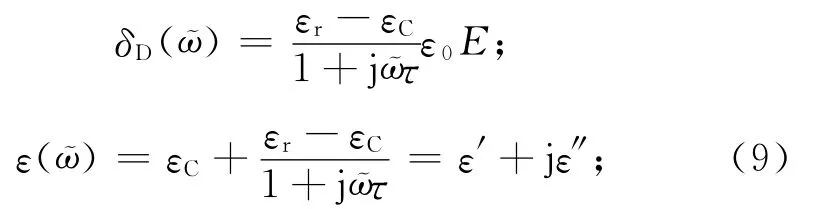
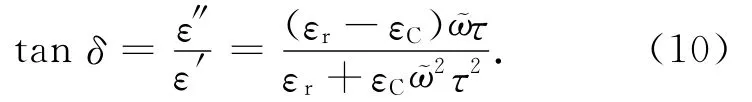
式中:ε′,ε″分別為ε(ω)的實部和虛部。
4 其他因素影響
由上述分析可知:除外場強外,溫度和時間均會影響電容。以電偶極子為例,外場強為零時,其三維方向的能量分布完全相同,偶極子一端在原點,另一端出現在以偶極子長度為單位長度,球面各點θ至θ+dθ圓環上概率與環面積2πsinθdθ成正比,平均偶極矩為零。當外電場為E,偶極子的位能與其方向有關,偶極子與電場方向夾角為θ,設其形變偶極矩為μ0,則位能變化ΔU=-Eμ0cosθ。由玻爾茲曼關系,電偶極子出現在方向夾角為θ區域的概率與exp[-ΔU/(kT)]成正比。此處:kT為熱學溫度。由此產生的偶極矩μ2為μ0cosθ,平均值
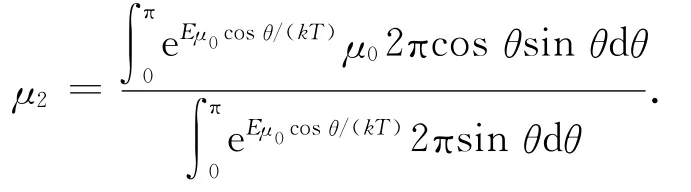
將exp[-Eμ0cosθ/(kT)]以級數形式展開,略去高次項,得

由式(11)可知:溫度升高,取向偶極矩變小;溫度下降,偶極矩變大。當取向偶極矩與溫度成反比關系,若場強不變,溫度上升使容量下降。從力學角度解釋,溫度上升,分子間無規則熱運動加劇,使取向極化趨于無規則化,與外場強相反的力矩變小,容量變大。
電老練后,可通過將電容再放回烘箱一段時間后減小其取向極化強度,使容量恢復。
5 實驗與分析
對CT41-2225-2C1-100V-225K,在溫度(125±2)℃、電壓200V、時間96h條件下老練,用HP4284對電老練前后的容量進行測試,結果見表1。由表1可知:老化后直接測試容量明顯變小,放置24h后容量有所恢復,而損耗經老化后參數變小,且不易恢復。
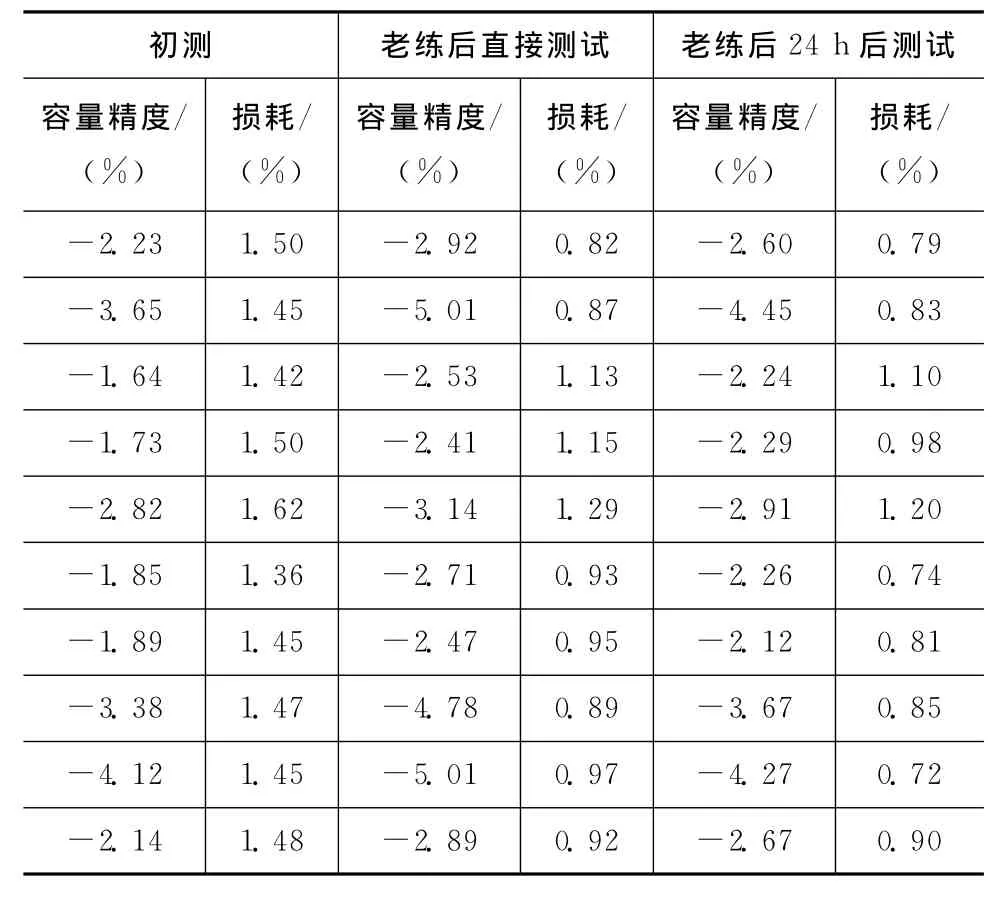
表1 CT41-2225-2C1-100V-225K試驗數據Tab.1 Test data of CT41-2225-2C1-100V-225K
對 CC41-1210-CG-100V-301J,在 溫 度 (125±2)℃、電壓200V、時間96h條件下老練,用HP4284對電老練前后的容量進行測試,結果見表2。由表可知:老化后直接測試容量明顯變小,放置24h后容量有所恢復,而損耗經老化后參數變化不大。
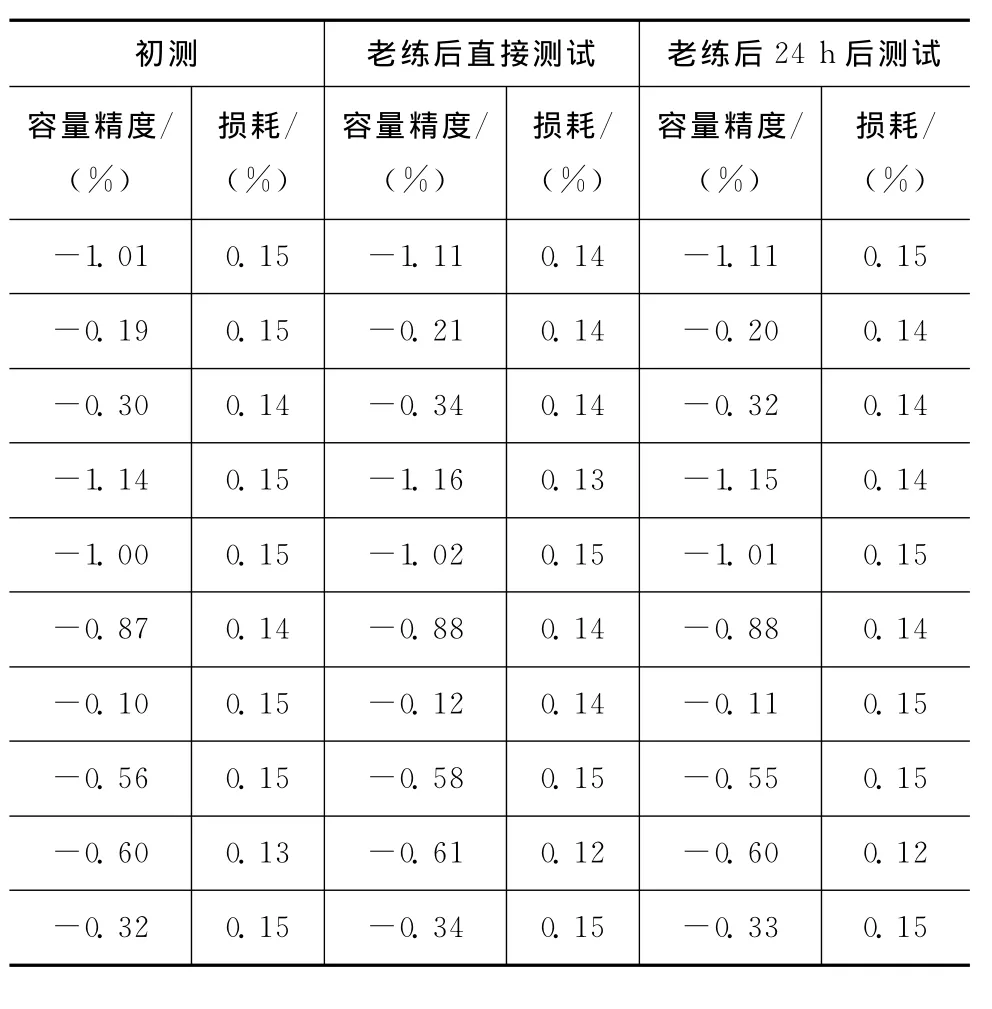
表2 CC41-1210-CG-100V-301J試驗數據Tab.2 Test data of CC41-1210-CG-100V-301J
對C73-100V-0.1μF-G,在溫度(85±2)℃,電壓120V,時間96h條件下老練,用HP4284對電老練前后的容量進行測試,結果見表3。由表可知:老化后直接測試容量明顯變小,放置24h后容量無明顯恢復,經14d后明顯恢復,而損耗經老化后,參數變小,需經較長時間恢復。由DPA試驗發現其內部電極結構無明顯異常,電極端并非導致容量變小原因,介質在高溫、加壓時產生變化,導致容量變化。
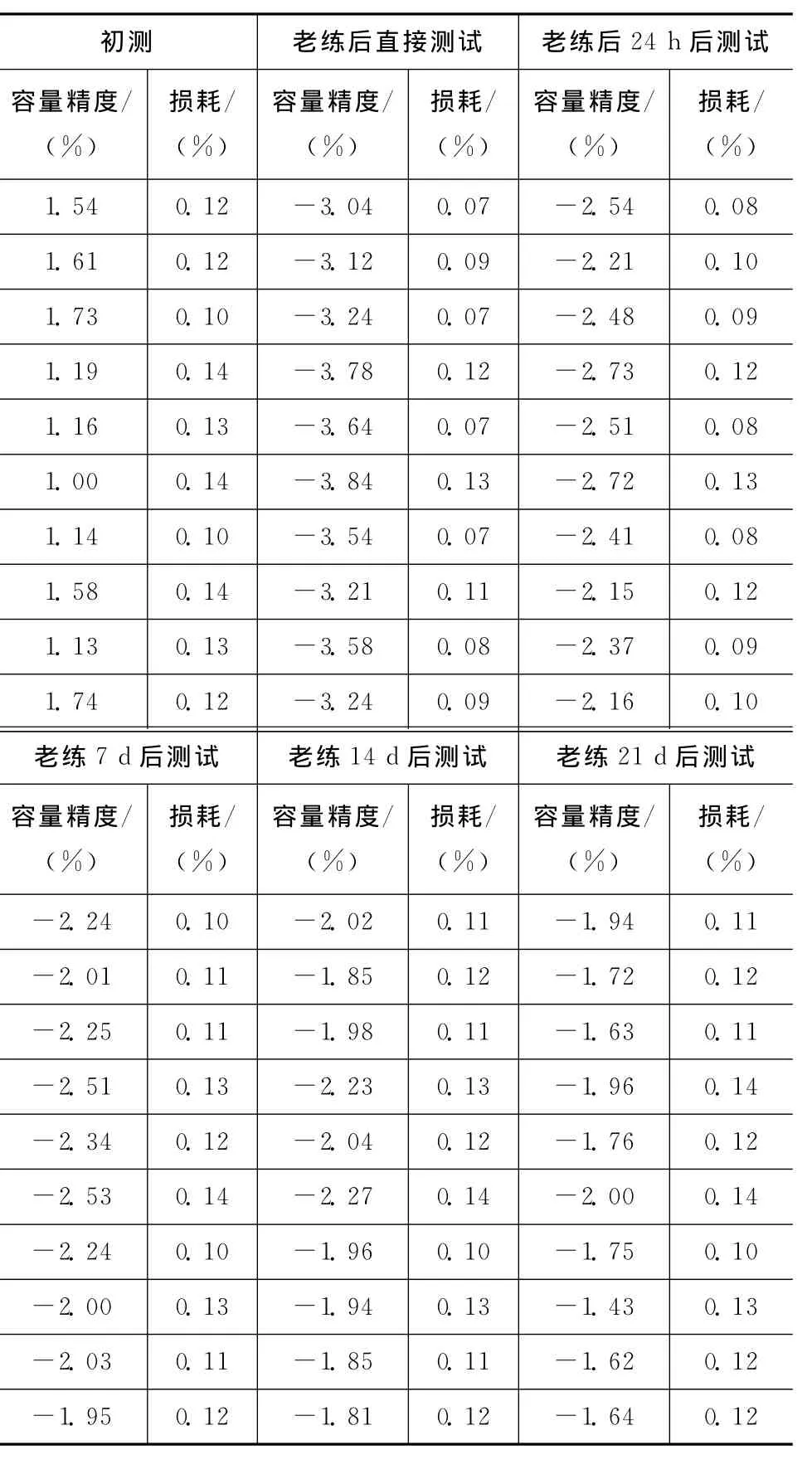
表3 C73-100V-0.1μF-G試驗數據Tab.3 Test data of C73-100V-0.1μF-G
上述實驗數據變化趨勢證明理論定性分析正確,電老練后因電偶極子受老練電壓和溫度影響,電偶極矩增大,反向電荷密度增加,容量減小,損耗減小。可知二類瓷介電容器的穩定性較一類瓷介電容器的穩定性差,去老練應力需一定時間。長期試驗結果表明:二類瓷介電容器需24h,也可將電容放回烘箱一段時間,效果較好。有機電容C73特性較不穩定,老練后測試需較長穩定時間,實際測試中老練后要2~3周才滿足測試精度。國軍標對電容去老練應力時間作了統一規定,沒有區分瓷介電容、有機電容等,與實際測試試驗不符。由于材料不同導致恢復時間不同,有機介質電容去應力時間至少為2周。
6 結束語
本文研究了電偶極子、電老練對電容參數的影響。電老練后,因電壓與溫度共同作用,介電常數發生變化,容量與損耗變小。不同種類的電容,因介質結構、特性各異,應制定不同的去應力時間以規范并便于測試操作:對瓷介電容去應力時間為24h,有機介質電容如C73(聚碳酸酯電容),其應力時間至少為2周;不能統一規定所有電容的去應力時間,應在對介質材料分析的基礎上,規定老化去應力時間,也可在產品的詳細規范或同類材料電容器的總規范中給出要求。
[1] 張三慧,臧庚媛,華基美.大學物理學 第3冊.電磁學[M].北京:清華大學出版社,2008.
[2] 顧振軍,王壽泰.聚合物的電性和磁性[M].上海:上海交通大學出版社,1990.
[3] 殷敬華,莫志深.現代高分子物理學[M].北京:科學出版社,2001.
[4] 盛 驟,謝式千,潘承毅.概率論與數理統計[M].北京:高等教育出版社,2008.
[5] 張啟仁.經典場論[M].北京:科學出版社,2001.
[6] 李正中.固體理論(第三版)[M].北京:高等教育出版社,2002.

