含區(qū)間參數(shù)的齒輪系統(tǒng)扭振固有特性研究

第一作者魏莎女，博士生，1988年2月生

通信作者褚福磊男，博士，教授，博士生導(dǎo)師，1959年9月生

郵箱：chufl@mail.dtinghua.edu.cn

含區(qū)間參數(shù)的齒輪系統(tǒng)扭振固有特性研究

魏莎，韓勤鍇，褚福磊(清華大學(xué)摩擦學(xué)國家重點(diǎn)實(shí)驗(yàn)室，北京100084)

摘要：為研究嚙合剛度等動(dòng)力學(xué)參數(shù)的波動(dòng)性對(duì)齒輪傳動(dòng)系統(tǒng)固有特性影響，以四自由度扭轉(zhuǎn)振動(dòng)齒輪傳動(dòng)系統(tǒng)模型為例，利用區(qū)間模態(tài)分析方法對(duì)含區(qū)間動(dòng)力學(xué)參數(shù)齒輪系統(tǒng)模態(tài)特性進(jìn)行分析。通過算例給出齒輪系統(tǒng)固有頻率波動(dòng)區(qū)間，并通過上下邊界相對(duì)不確定量與曲線凹凸性分析區(qū)間參數(shù)對(duì)系統(tǒng)固有頻率影響。結(jié)果表明，參數(shù)波動(dòng)導(dǎo)致的區(qū)間固有頻率并非關(guān)于確定性模型下固有頻率中心對(duì)稱，而存在上下偏差，導(dǎo)致該偏差的主要原因?yàn)榍€凹凸性；通過上下邊界相對(duì)不確定量及凹凸性可判斷固有頻率隨系統(tǒng)參數(shù)的波動(dòng)規(guī)律，上下邊界相對(duì)不確定量間差異越大曲線凹凸性越明顯。在單區(qū)間參數(shù)分析中，不同區(qū)間動(dòng)力學(xué)參數(shù)對(duì)系統(tǒng)固有頻率影響不同。當(dāng)所有參數(shù)區(qū)間波動(dòng)均考慮時(shí)系統(tǒng)區(qū)間固有頻率范圍最大，超過工程能接受結(jié)果，因此設(shè)計(jì)分析時(shí)參數(shù)的區(qū)間波動(dòng)性不可忽略。

關(guān)鍵詞：齒輪；固有頻率；模態(tài)；區(qū)間分析

收稿日期：2014-03-10修改稿收到日期：2014-04-30

中圖分類號(hào):TH132.41；TH113.1文獻(xiàn)標(biāo)志碼：A

Natural characteristics analysis for torsional vibration of a geared transmission system with uncertainties

WEISha,HANQin-kai,CHUFu-lei(State Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China)

Abstract:The torsional vibration model of a geared transmission system with 4-DOF was developed to study the natural characteristics of a gear system considering fluctuations of tooth mesh stiffness and other dynamic parameters. The interval modal analysis method, relative uncertainties and the curve concavity and convexity analysis were used to investigate the modal characteristics of the gear system with interval varying dynamic parameters. The fluctuation intervals of its natural frequencies were obtained with a numerical example. The results showed that the natural frequencies of the deterministic model are not the central values of the interval varying natural frequencies caused by parameter fluctuations, there are upper and lower deviations caused by the curve concavity and convexity; the fluctuating laws of the natural frequencies with fluctuating parameters can be determined with the relative uncertainties of the upper and lower bounds and the curve concavity and convexity; the greater the differences between the relative uncertainties of the upper and lower bounds, the more obvious the corresponding curve concavity and convexity; the effects of different interval dynamic parameters on the natural frequencies are different in a single interval parametric analysis; the interval natural frequencies are largest and exceed the acceptable results of engineering when the fluctuations of all the corresponding parameters are taken into account; therefore, the effects of the interval fluctuations of system parameters on the natural frequencies of the gear system can not be ignored.

Key words:gear; natural frequencies; modal; interval analysis

齒輪傳動(dòng)系統(tǒng)廣泛用于風(fēng)力發(fā)電機(jī)組、直升機(jī)、汽車等機(jī)械設(shè)備。對(duì)其進(jìn)行深入的動(dòng)力學(xué)研究可為設(shè)備的安全、優(yōu)化設(shè)計(jì)及可靠性評(píng)估奠定基礎(chǔ)。目前齒輪系統(tǒng)動(dòng)力學(xué)研究大多處理為確定性問題[1-3]，但制造、裝配、潤滑、沖擊及溫度等因素會(huì)導(dǎo)致齒輪系統(tǒng)參數(shù)具有不確定性，且理論分析的動(dòng)力學(xué)模型往往進(jìn)行一定簡化，與實(shí)際模型存在誤差，因此須進(jìn)行不確定參數(shù)下的特性分析。齒輪系統(tǒng)動(dòng)態(tài)特性不確定分析主要采用基于統(tǒng)計(jì)模型的分析方法[4-6]，而不確定性不等同于隨機(jī)性，統(tǒng)計(jì)分析方法并非研究齒輪不確定問題的唯一方法。實(shí)際上，不確定分析的相關(guān)數(shù)學(xué)模型有統(tǒng)計(jì)模型、區(qū)間模型及模糊模型等，需針對(duì)具體問題據(jù)已知相關(guān)信息程度選擇相應(yīng)數(shù)學(xué)模型進(jìn)行不確定性分析。其中區(qū)間模型無需大量樣本實(shí)驗(yàn)或參數(shù)分布假設(shè)，在已知參數(shù)邊界信息情況下，用相關(guān)區(qū)間算法給出結(jié)果所在區(qū)間及結(jié)果誤差估計(jì)。區(qū)間分析方法在土木結(jié)構(gòu)的模態(tài)特性分析中已有研究成果，如陳塑寰[7]提出的矩陣攝動(dòng)法給出在小擾動(dòng)下區(qū)間特征值的近似計(jì)算方法。Sim等[8]給出的計(jì)算結(jié)構(gòu)系統(tǒng)模態(tài)區(qū)間分析方法，將n個(gè)區(qū)間特征值問題轉(zhuǎn)化為2n個(gè)確定性特征值求解。而區(qū)間分析方法用于齒輪傳動(dòng)系統(tǒng)固有特性分析的相關(guān)研究較少。本文針對(duì)貧信息、小樣本下已知參數(shù)信息，利用區(qū)間分析方法對(duì)具有區(qū)間參數(shù)的齒輪系統(tǒng)固有特性進(jìn)行研究，并給出固有頻率所在區(qū)間，分析區(qū)間參數(shù)對(duì)系統(tǒng)固有頻率影響。

1系統(tǒng)模型及固有特性分析

圖1為單對(duì)齒輪傳動(dòng)系統(tǒng)示意圖，輸入原動(dòng)機(jī)、主被動(dòng)齒輪及輸出負(fù)載均等效為圓柱體，其中主被動(dòng)齒輪等效圓柱厚度相同。圖中Im、I1、I2、IL分別表示輸入原動(dòng)機(jī)、主動(dòng)齒輪、從動(dòng)齒輪、負(fù)載的轉(zhuǎn)動(dòng)慣量，km為齒輪副嚙合剛度，ks1、ks2分別為主、被動(dòng)連接軸扭轉(zhuǎn)剛度，θm、θ1、θ2、θL為輸入原動(dòng)機(jī)、主動(dòng)齒輪、從動(dòng)齒輪、負(fù)載的扭轉(zhuǎn)角位移，Tm、TL分別為作用于原動(dòng)機(jī)、負(fù)載的外力矩。

圖1　齒輪傳動(dòng)系統(tǒng)純扭轉(zhuǎn)振動(dòng)模型 Fig.1 Schematic diagram of torsional vibration model

本文僅研究齒輪傳動(dòng)系統(tǒng)的固有特性，其自由振動(dòng)方程[9]為

(1)

式中：θ為振動(dòng)位移向量；m，k分別為質(zhì)量、剛度矩陣。具體表達(dá)式為

θ=[θmθ1θ2θL]T

(2)

(3)

(4)

主被動(dòng)齒輪基圓半徑R1、R2及轉(zhuǎn)動(dòng)慣量I1、I2以及主被動(dòng)連接軸扭轉(zhuǎn)剛度ks1、ks2計(jì)算式為

R1=mz1cos(α0/2),R2=mz2cos(α0/2)

(5)

(6)

(7)

式中：ρ為質(zhì)量密度；b為有效齒寬；G為剪切模量，可由式(8)求得；m為齒輪模數(shù)；α0為壓力角；z1，z2為主、被動(dòng)輪齒數(shù)；Ra1，Ra2為主、被動(dòng)連接軸半徑；la1，la2為主、被動(dòng)連接軸長。

G=E/(2(1+υ))

(8)

式中：E為彈性模量；υ為泊松比。

確定性參數(shù)下的第i階特征值λi滿足

kΦi=λimΦi

(9)

式中：Φi為λi對(duì)應(yīng)的主振型(質(zhì)量正則化)。

取齒輪傳動(dòng)系統(tǒng)基本參數(shù)[10]見表1，計(jì)算得確定參數(shù)下固有頻率為0 Hz、266 Hz、524 Hz、3362 Hz，振型見圖2。圖2中點(diǎn)劃線表示模態(tài)參考位置，實(shí)線表示由確定性參數(shù)計(jì)算所得模態(tài)陣型。由圖2看出，二階模態(tài)在負(fù)載處振動(dòng)最大，其次為原動(dòng)機(jī)，而主被動(dòng)齒輪處振動(dòng)不明顯。

表1　基本計(jì)算參數(shù)

圖2　齒輪系統(tǒng)振型圖 Fig.2 Mode shapes of the gear system

2區(qū)間模態(tài)分析

以上為齒輪傳動(dòng)系統(tǒng)扭轉(zhuǎn)振動(dòng)的確定性模態(tài)分析。而材料不均勻性、制造誤差、測量誤差及潤滑等因素會(huì)導(dǎo)致系統(tǒng)的剛度、質(zhì)量參數(shù)只能給出其近似值及絕對(duì)誤差界限。本文中用區(qū)間參數(shù)表示為

aI=[ac-βac,ac+βac]

(10)

式中：aI為區(qū)間參數(shù)；ac為區(qū)間參數(shù)近似值；β為區(qū)間參數(shù)波動(dòng)誤差。

考慮參數(shù)的區(qū)間波動(dòng)，原自由振動(dòng)方程(1)轉(zhuǎn)化為區(qū)間約束下振動(dòng)方程為

(11)

式中：m，k為質(zhì)量、剛度矩陣，滿足

(12)

(13)

Chen等[11]基于Rayleigh商給出用于計(jì)算區(qū)間特征值問題的非迭代方法，其中第i階特征值上下邊界值可直接由計(jì)算式獲得，即

(14)

為考察各系統(tǒng)參數(shù)存在區(qū)間波動(dòng)時(shí)系統(tǒng)固有頻率變化，取相應(yīng)參數(shù)為區(qū)間參數(shù)。區(qū)間原動(dòng)機(jī)轉(zhuǎn)動(dòng)慣量可表示為

(15)

為分析方便，定義上、下邊界相對(duì)不確定量μupper，μlower分別為

(16)

式中：

(17)

(18)

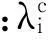
為驗(yàn)證本文齒輪系統(tǒng)動(dòng)力學(xué)模型的正確性及區(qū)間分析方法精度及效率，考慮Im、I1、I2、IL均為區(qū)間參數(shù)，采用Monte Carlo分析方法對(duì)該算例固有頻率模擬計(jì)算。其中區(qū)間參數(shù)近似值由表1取得。波動(dòng)誤差均為5%，統(tǒng)計(jì)分析樣本數(shù)分別取1000、10000、100000，計(jì)算效率比較結(jié)果見表 2。由表2看出，區(qū)間分析方法耗時(shí)最短，而Monte Carlo分析方法計(jì)算時(shí)間隨樣本數(shù)增加而增加。較Monte Carlo分析方法，區(qū)間分析方法大大節(jié)省計(jì)算時(shí)間。Monte Carlo仿真取樣100000次與區(qū)間分析方法對(duì)比結(jié)果見圖3。由圖3看出，區(qū)間分析方法結(jié)果較好包絡(luò)Monte Carlo仿真分析結(jié)果。

表2　兩種不確定分析方法計(jì)算效率比較

考慮Im、I1、I2、IL、km、ks1、ks2均為區(qū)間參數(shù)時(shí)，波動(dòng)誤差均取5%，利用各矩陣對(duì)區(qū)間參數(shù)的單調(diào)性可得對(duì)應(yīng)區(qū)間質(zhì)量、剛度矩陣分別為

圖3 區(qū)間分析方法與蒙特卡洛仿真方法結(jié)果對(duì)比Fig.3ComparisonbetweentheintervalmethodandtheMonteCarlomethodwithfluctuationsofmomentsofinertia圖4 齒輪系統(tǒng)區(qū)間固有頻率及不確定量隨β變化規(guī)律Fig.4Curvesofnaturalfrequenciesandrelativeuncertaintieswithfluctuationerrors

由式(14)所得第二階固有頻率見表 3。由表3看出，固有頻率并非確定值，而是一個(gè)區(qū)間，且當(dāng)相關(guān)動(dòng)力學(xué)參數(shù)均考慮為區(qū)間參數(shù)，β取5%時(shí)，計(jì)算所得fn2的相對(duì)不確定量已達(dá)6%，超出工程能接受限值。圖4為fn2隨β及μlower、μupper隨β的變化規(guī)律。由圖4看出，隨β增大齒輪系統(tǒng)固有頻率區(qū)間寬度線性增大。當(dāng)β達(dá)到15%時(shí)fn2的相對(duì)不確定量達(dá)18%，遠(yuǎn)超工程接受范圍。因此在設(shè)計(jì)階段，參數(shù)的區(qū)間波動(dòng)性分析不可忽略。

表3　齒輪系統(tǒng)區(qū)間固有頻率

2.1區(qū)間質(zhì)量參數(shù)對(duì)固有頻率影響

Im、I1、I2、IL分別為區(qū)間參數(shù)時(shí)所得fn2及μlower、μupper隨β變化規(guī)律見圖 5～圖8。由4圖看出，不同區(qū)間動(dòng)力學(xué)參數(shù)對(duì)系統(tǒng)固有頻率影響亦不同。其中區(qū)間參數(shù)波動(dòng)誤差對(duì)齒輪系統(tǒng)區(qū)間固有頻率影響明顯，隨β增大fn2線性增大；在Im、IL對(duì)fn2影響中，μlower、μupper不相等。該差異主要由參數(shù)的凹凸性所致，具體分析見圖9。由圖9看出，當(dāng)函數(shù)曲線為凹弧時(shí)，對(duì)稱參數(shù)區(qū)間對(duì)應(yīng)的函數(shù)結(jié)果并非關(guān)于確定性模型下結(jié)果對(duì)稱，而是上邊界相對(duì)不確定量大于下邊界；當(dāng)函數(shù)曲線為凸弧時(shí)，對(duì)稱參數(shù)區(qū)間對(duì)應(yīng)的函數(shù)結(jié)果亦非關(guān)于確定性模型下結(jié)果對(duì)稱，而是下邊界相對(duì)不確定量大于上邊界；且凹凸性越明顯對(duì)應(yīng)上下邊界相對(duì)不確定量間差異越大。因此圖5中μupper> μlower現(xiàn)象主要因Im與fn2間曲線關(guān)系為凹弧導(dǎo)致。由圖5(c)看出，Im與fn2間曲線關(guān)系為凹弧，驗(yàn)證了通過上下邊界相對(duì)不確定量得

圖5　各種變化規(guī)律 Fig.5 Curves of natural frequencies

圖6　各種變化規(guī)律 Fig.6 Curves of natural frequencies

圖7　各種變化規(guī)律 Fig.7 Curves of natural frequencies

圖8　各種變化規(guī)律 Fig.8 Curves of natural frequencies

到的推斷。圖8現(xiàn)象原因相同，不再贅述。圖6(b)中當(dāng)I1為區(qū)間參數(shù)時(shí)，fn2的相對(duì)不確定量隨β線性增加；在相同波動(dòng)誤差下，上下邊界相對(duì)不確定量相等。主要因I1與fn2間為線性關(guān)系，見圖6(c)。圖7(b)中，當(dāng)I2為區(qū)間參數(shù)時(shí)fn2的相對(duì)不確定量隨β線性增加；在相同波動(dòng)誤差下，上下邊界相對(duì)不確定量近似相等，主要因I2與fn2間曲線關(guān)系近似線性，見圖7(c)。

圖9　曲線凹凸性分析 Fig.9 Concavity and convexity analysis

2.2區(qū)間剛度參數(shù)對(duì)固有頻率影響

由于誤差、碰撞及潤滑等原因?qū)е聡Ш蟿偠仍邶X輪嚙合轉(zhuǎn)動(dòng)過程中存在不確定性波動(dòng)，且在嚙合剛度解析計(jì)算中所得結(jié)果與實(shí)測值誤差一般在20%內(nèi)[12]。考慮km、ks1、ks2為區(qū)間參數(shù)時(shí)，可得相應(yīng)的fn2隨β變化規(guī)律及μlower、μupper隨β變化規(guī)律見圖10～圖12。由圖10(a)、(b)看出，隨β增大fn2非線性增大；在相同波動(dòng)誤差下μlower與μupper間差異較大，且μlower明顯大于μupper，主要由嚙合剛度與固有頻率間曲線關(guān)系為凸弧引起，見圖10(c)。由此表明齒輪嚙合剛度對(duì)系統(tǒng)固有特性影響顯著，應(yīng)予以考慮。而ks2對(duì)fn2影響最明顯，且為線性，見圖12(c)。當(dāng)β < 5%時(shí)km、ks1對(duì)fn2影響較小，而β繼續(xù)增加時(shí)fn2的區(qū)間上下界差異明顯。圖11(b)中表現(xiàn)為μlower> μupper，主要因ks1與fn2的曲線關(guān)系為凸弧，見圖11(c)。

圖10　各種變化規(guī)律 Fig.10 Curves of natural frequencies

圖11　各種變化規(guī)律 Fig.11 Curves of natural frequencies

圖12　各種變化規(guī)律 Fig.12 Curves of natural frequencies

3結(jié)論

(1)較Monte Carlo仿真等統(tǒng)計(jì)分析方法，區(qū)間模型無需大量樣本實(shí)驗(yàn)及概率假設(shè)，結(jié)果可靠，節(jié)省計(jì)算成本。對(duì)具有不確定參數(shù)的動(dòng)力學(xué)系統(tǒng)特性，據(jù)已知系統(tǒng)信息程度選擇不同分析方法。系統(tǒng)參數(shù)信息無法獲得或只能進(jìn)行有限實(shí)驗(yàn)時(shí)，區(qū)間分析方法可直觀給出計(jì)算結(jié)果的區(qū)間范圍及相應(yīng)誤差估計(jì)。

(2)考慮系統(tǒng)動(dòng)力學(xué)參數(shù)存在區(qū)間波動(dòng)時(shí)所得固有頻率也在一個(gè)區(qū)域內(nèi)波動(dòng)。且參數(shù)波動(dòng)導(dǎo)致的區(qū)間固有頻率并非關(guān)于確定性模型下固有頻率中心對(duì)稱，而存在上下偏差，主要原因?yàn)閰?shù)的凹凸性。通過凹凸性、上下邊界相對(duì)不確定量可判斷系統(tǒng)參數(shù)波動(dòng)規(guī)律，進(jìn)而推斷區(qū)間固有頻率受參數(shù)波動(dòng)應(yīng)注意的地方。

(3)當(dāng)考慮所有參數(shù)區(qū)間波動(dòng)時(shí)，系統(tǒng)區(qū)間固有頻率范圍最大。雖各動(dòng)力學(xué)參數(shù)波動(dòng)誤差均較小，但累加后對(duì)固有頻率影響較顯著。設(shè)計(jì)時(shí)參數(shù)的區(qū)間波動(dòng)性分析不可忽略。

(4)不同區(qū)間動(dòng)力學(xué)參數(shù)對(duì)系統(tǒng)固有頻率影響不同。區(qū)間參數(shù)的波動(dòng)誤差對(duì)齒輪系統(tǒng)區(qū)間固有頻率影響明顯。第二階固有頻率主要受負(fù)載轉(zhuǎn)動(dòng)慣量及被動(dòng)連接軸扭轉(zhuǎn)剛度影響。

(5)分別在原動(dòng)機(jī)轉(zhuǎn)動(dòng)慣量、負(fù)載轉(zhuǎn)動(dòng)慣量、主動(dòng)連接軸的扭轉(zhuǎn)、嚙合剛度對(duì)固有頻率影響分析中，上下邊界相對(duì)不確定量不相等，由凹凸性可判斷其與固有頻率間關(guān)系。主被動(dòng)齒輪的轉(zhuǎn)動(dòng)慣量、被動(dòng)連接軸扭轉(zhuǎn)剛度與第二階固有頻率變化規(guī)律均為線性關(guān)系。

參考文獻(xiàn)

[1]Han Q, Zhao J, Chu F. Dynamic analysis of a geared rotor system considering a slant crack on the shaft [J]. Journal of Sound and Vibration, 2012, 331(26): 5803-5823.

[2]Parker R G, Wu X. Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear [J]. Journal of Sound and Vibration, 2010, 329(11): 2265-2275.

[3]楊通強(qiáng)，宋軼民，張策，等. 斜齒行星齒輪系統(tǒng)自由振動(dòng)特性分析[J]. 機(jī)械工程學(xué)報(bào), 2005, 41(7): 50-55.

YANG Tong-qiang, SONG Yi-min, ZHANG Ce,et.al. Property analysis of free vibration of helical planetary gear trains [J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 50-55.

[4]李潤方，王建軍. 國外齒輪系統(tǒng)動(dòng)態(tài)特性的統(tǒng)計(jì)分析[J]. 機(jī)械傳動(dòng), 1995, 19(4): 45-47.

LI Run-fang, WANG Jian-jun. Statistical analysis of characteristics for gear system at overseas[J]. Journal of Mechanical Transmission, 1995, 19(4): 45-47.

[5]Driot N, Perret-Liaudet J. Variability of modal behavior in terms of critical speeds of a gear pair due to manufacturing errors and shaft misalignments[J]. Journal ofSound and Vibration, 2006, 292(3): 824-843.

[6]魏永祥，陳建軍，王敏娟. 隨機(jī)參數(shù)齒輪-轉(zhuǎn)子系統(tǒng)扭轉(zhuǎn)振動(dòng)固有頻率分析[J]. 工程力學(xué), 2011, 28(4): 172-177.

WEI Yong-xiang, CHEN Jian-jun, WANG Min-juan. Natural frequency analysis for torsional vibration of a gear-rotor system with random parameters [J]. Engineering Mechanics, 2011, 28(4): 172-177.

[7]陳塑寰. 結(jié)構(gòu)動(dòng)態(tài)設(shè)計(jì)的矩陣攝動(dòng)理論[M]. 北京: 科學(xué)出版社, 1999.

[8]Sim J, Qiu Z, Wang X. Modal analysis of structures with uncertain-but-bounded parameters via interval analysis[J]. Journal of Sound and Vibration, 2007, 303(1/2): 29-45.

[9]李潤方，王建軍. 齒輪系統(tǒng)動(dòng)力學(xué)-振動(dòng)、沖擊、噪聲[M]. 北京: 科學(xué)出版社, 1997.

[10]Kahraman A, Ozguven H N, Houser D R, et al. Dynamic analysis of geared rotors by finite elements[R]. DTIC Document, 1990.

[11]Chen S, Qiu Z, Song D. A new method for computing the upper and lower bounds on frequencies of structures with interval parameters [J]. Mechanics Research Communications, 1994, 21(6): 583-592.

[12]李明，孫濤，胡海巖. 齒輪傳動(dòng)轉(zhuǎn)子-軸承系統(tǒng)動(dòng)力學(xué)的研究進(jìn)展[J]. 振動(dòng)工程學(xué)報(bào), 2002, 15(3): 5-12.

LI Ming, SUN Tao, HU Hai-yan. Review on dynamics of geared rotor-bearing systems[J]. Journal of Vibration Engineering, 2002, 15(3): 5-12.