含區間參數的結構-聲耦合系統攝動分析方法
第一作者牛明濤男,碩士,工程師,1986年8月生
含區間參數的結構-聲耦合系統攝動分析方法
牛明濤,李昌盛,陳利源(中國石化石油工程技術研究院,北京100101)
摘要:針對實際工程中普遍存在的結構-聲耦合系統,充分考慮系統本身及外載荷不確定性,基于攝動理論建立一階及高階參數攝動兩種區間分析方法。從耦合系統有限元平衡方程出發,引入區間變量對系統不確定參數進行定量化描述。據傳統的一階Taylor展式及攝動理論,可快速估算系統響應區間上下界。高階區間參數攝動分析方法除采用改進的Taylor展式對區間矩陣、向量近似估算外,亦保留Neumann級數中部分高階項,可有效提高響應范圍的計算精度。以長方體密閉艙室為研究對象,將計算結果與傳統蒙特卡洛方法對比,充分驗證所提數值計算方法求解含區間參數結構-聲耦合問題的可行性、有效性。
關鍵詞:結構-聲耦合系統;區間不確定性;區間參數攝動方法;Neumann級數
基金項目:中國石化“十二五”重點信息化項目 (G11-MM-2011-080);中國石化重點科技攻關項目(P13093)
收稿日期:2014-03-26修改稿收到日期:2014-05-16
中圖分類號:O328;O422.6文獻標志碼:A
Perturbation methods for structural-acoustic coupled systems with interval parameters
NIUMing-tao,LIChang-sheng,CHENLi-yuan(Sinopec Research Institute of Petroleum Engineering, Beijing 100101, China)
Abstract:Based on the perturbation theory, two interval analysis methods named first-order interval parameter perturbation method (FIPPM) and high-order interval parameter perturbation method (HIPPM) were proposed for the structural-acoustic coupled system response prediction with interval uncertainties in both system parameters and external loads. The structural-acoustic discrete equilibrium equations were established based on the finite element method. Interval variables were used to quantitatively describe the uncertain parameters with limited information. According to the first-order Taylor series and the first-order perturbation theory, the system response interval could be quickly estimated with FIPPM. HIPPM introduced the modified Taylor series to approximately estimate the non-linear interval matrix and vector. Part of higher order terms of Neumann expansion were retained to calculate the interval matrix inverse. A 3D cuboid model was taken as a study object, its computing results using the propose methods were compared with those using the traditional Monte Carlo method. It was shown that the proposed methods are feasible and effective to predit the sound pressure ranges of structural-acoustic coupled systems.
Key words:structural-acoustic coupled system; interval uncertainty; interval parameter perturbation method; Neumann series
工程設計通常希望降低有害振動及噪聲幅值以提升系統的安全性、舒適性。而柔性結構振動與充滿流體介質封閉聲場之間的耦合問題較多見,其聲場內部噪聲由結構振動引起。若考慮內部聲壓對結構的反作用,該系統稱結構-聲耦合系統,在汽車、航空、船舶等工業領域普遍存在[1]。對此類系統中、低頻響應的數值分析主要用有限元[2]、邊界元[3]兩種方法對聲場進行離散。工程中,材料物理參數與邊界條件會受多種不確定性因素影響,由此引起結構振動聲輻射呈一定程度不確定性。處理此類不確定聲學問題的常用方法主要源于概率理論,James等[4]通過將不確定參數定量化,研究確定聲場概率密度函數的計算方法。Finette[5]提出隨機響應面方法預測海洋不確定環境下聲場的傳播規律。Liu等[6]給出基于有限-邊界元方法、虛擬激勵原理的隨機結構振動聲輻射靈敏度問題解決方法。
建立概率模型需預知不確定量的概率密度函數,而足夠的信息往往預先難以獲得。相比之下,區間方法僅需用少量信息確定不確定參數的上下界,具有較好的方便性、經濟性[7]。與處理區間問題常用的蒙特卡洛方法[8]、頂點法[9]相比,攝動方法[10]憑借其獨特的計算效率頗受關注[11]。隨不確定性定量精細化發展趨勢,傳統攝動方法因忽略高階項所致計算精度問題日益嚴重。鑒于此,本文以含區間參數的結構-聲耦合系統為研究對象,提出改進的高階區間參數攝動方法,可保留Neumann級數中部分高階項。通過數值算例驗證該方法有效性,且能滿足工程對計算效率、精度需求。
1結構-聲耦合系統有限元方程
針對圖1結構-聲耦合系統,在頻域分析下,內部聲場壓強p可由Helmholtz方程表示,即
(1)
據變分原理,得具有彈性邊界聲場的有限元方程為
(Ka+jωCa-ω2Ma)P=ρω2SUs
(2)
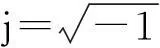

圖1 結構-聲耦合系統模型 Fig.1 Model of the coupled structural-acoustic system
充分考慮內部聲壓對結構的反作用,在頻域下結構有限元運動方程為
(KsjωCs-ω2Ms)Us=Fs+STP
(3)
式中:Ks,Ms,Cs分別為結構剛度、質量、阻尼矩陣;Fs為施加于結構的外力。
聯合式(2)、式(3),得結構-聲耦合系統有限元方程為
(-ω2M+jωC+K)U=F
(4)
式中:
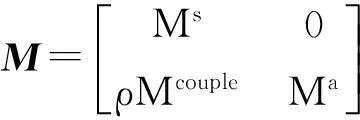
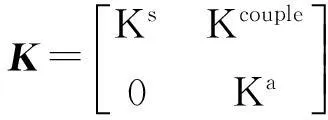
Mcouple=S;Kcouple=-ST
為表示方便,將式(4)記為
AU=F
(5)
式中:
A=-ω2M+jωC+K
(6)
實際問題中,由于工藝限制及環境變化等因素,結構-聲耦合系統存在大量不確定性。本文引入如區間向量表示所有不確定參數,即
(7)

顯然,式(4)中系數矩陣及右端向量均與此區間向量相關聯。因此,耦合有限元方程(5)可改寫為
A(αI)U(αI)=F(αI)
(8)
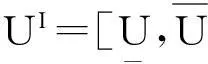
A(αI)UI=F(αI)
(9)
2一階區間參數攝動分析方法
將式(9)中系數矩陣及右端向量在區間參數中值處進行一階Taylor展開,得
(10)
(11)
用中心區間表示方法將系統響應記為UI=Uc+ΔUI,將式(10)、(11)代入式(9),得
(Ac+ΔAI)(Uc+ΔUI)=Fc+ΔFI
(12)
忽略二階及以上高階小量,利用攝動理論得
(13)
考慮矩陣Ac總可逆,故有
Uc=(Ac)-1Fc
(14)
ΔUI=(Ac)-1(ΔFI-ΔAI(Ac)-1Fc)
(15)
將式(10)、(11)代入式(15),得
ΔUI=
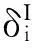
ΔU=
因此,利用一階區間參數攝動分析方法獲得結構-聲耦合系統區間響應上、下界分別為
(18)
3高階區間參數攝動分析方法
區間不確定參數變化范圍較大或數量較多時,忽略高階項的一階參數攝動方法所致區間擴張問題有時較嚴重。為此,基于改進的Taylor展式、Neumann級數,提出高階區間參數攝動分析方法。通過空間近似曲面導軌生成方式[12]獲得(9)系數矩陣的近似表示
A(αI)=A(α1,α2,…,αm)=
(19)
式中:
(20)
(21)
式中:
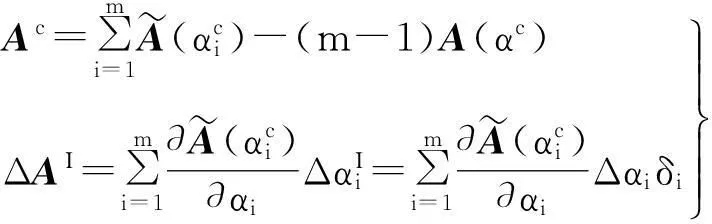
(22)
用相同處理方式,區間參數向量F(αI)可表示為
(23)
式中:
(24)
將式(21)、(23)代入式(9),兩邊左乘(Ac+ΔAI)-1得
Uc+ΔUI=(Ac+ΔAI)-1(Fc+ΔFI)
(25)
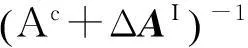
(Ac+ΔAI)-1=(Ac)-1+
(26)
借助式(22)得
(27)

針對不同r值,上式可表示為
(28)
將式(27)、(28)代入式(26),得
(29)
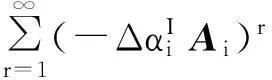
(30)
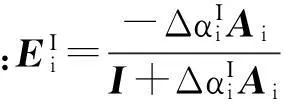
(31)
(32)
將式(30)代入式(25),利用攝動理論,忽略高階交叉向量,得
(33)
(34)
利用式(24),將式(34)改寫為
(35)
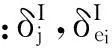
(36)
利用高階區間參數攝動分析方法所得結構-聲耦合系統區間響應上、下界分別為
(37)
4數值算例
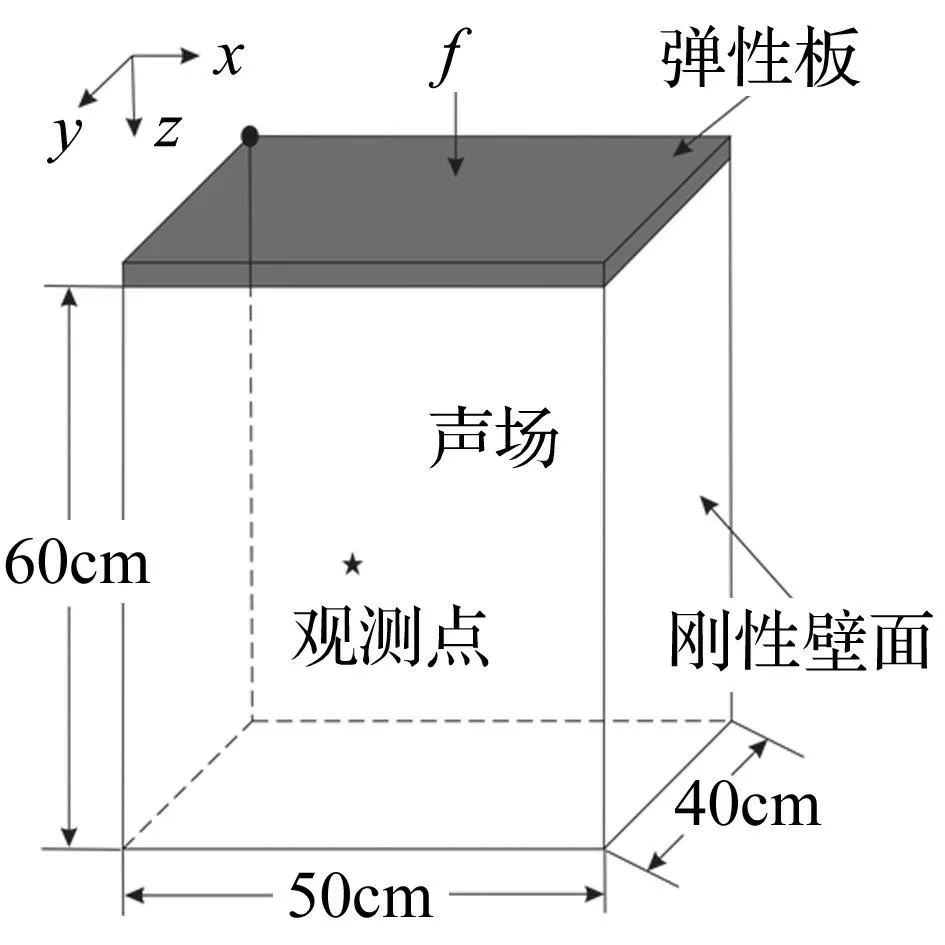
圖2 長方體密閉艙室模型 Fig.2 Model of acuboid airtight cabin
考慮圖2的長50 cm、寬40 cm、高60 cm長方體艙室模型,四周由同一種鋁合金材料圍成封閉空間,內部充滿空氣介質,構成結構-聲耦合系統。其中艙室頂部為2 mm厚彈性鋁板,其余為剛性壁面。由于材料的初始缺陷,鋁合金密度、彈性模量分別在2 565~2 835 kg/m3及67.5~74.5 GPa范圍變化。因周圍溫度環境變化,空氣密度、聲速被認為區間不確定參數,其變化區間分別為[1.164,1.286] kg/m3,[323,357]m/s。有一簡諧激勵作用于頂部鋁板中心處,激勵幅值為[0.95,1.05] N,計算0~300 Hz頻域范圍聲腔觀測點的聲壓值。
由傳統蒙特卡洛方法(MCM)的概率收斂特征知,隨樣本的不斷增加,由隨機抽樣計算所得響應區間逐漸收斂于真實解。故本算例中經105隨機抽樣所得聲壓響應區間作為參考解,驗證區間參數攝動方法精度。利用本文一階區間參數攝動分析方法(FIPPM)及高階區間參數攝動分析方法(HIPPM)求解含不確定參數的結構-聲耦合有限元方程,觀測點聲壓范圍上界(UB)、下界(LB) 及相對誤差見表1。由表1看出,高階攝動方法相對誤差遠小于一階攝動方法,表明在求矩陣逆過程中,通過保留Neumann展式的部分高階項可有效提高參數攝動方法計算精度;對計算耗時而言,高階攝動方法程序運行時間稍高于一階攝動方法,復雜問題會更明顯。考慮高階攝動方法對計算精度的有效改善,運行時間稍長完全可接受。
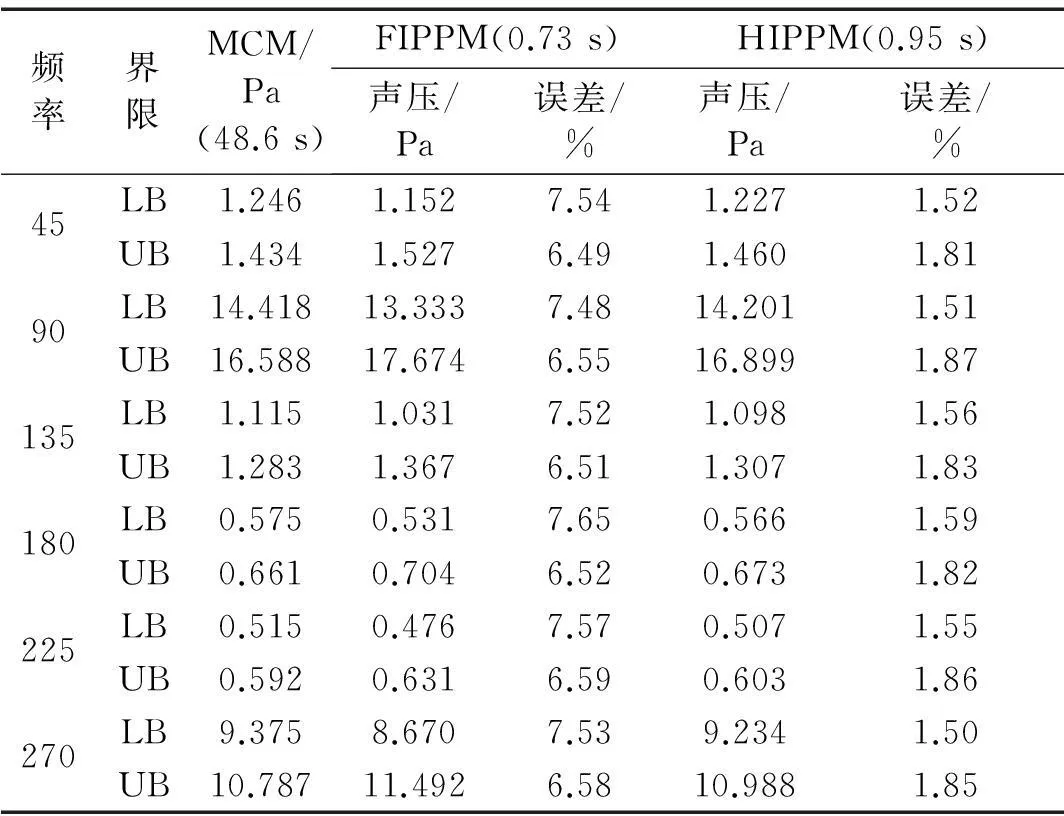
表1 聲壓幅值區間界限及相對誤差
在0~300 Hz內,由三種方法計算所得聲壓幅值區間見圖3。與一階攝動方法結果相比,高階攝動方法在整個頻域范圍內的頻響區間均較小。與蒙特卡洛模擬所得參考值相比,高階攝動方法仍存在一定區間擴張,但差別較小。精度要求不太高時,高階攝動方法所得結果完全可信,且可有效減少大量隨機抽樣所致計算耗費,從而有效提高計算效率。
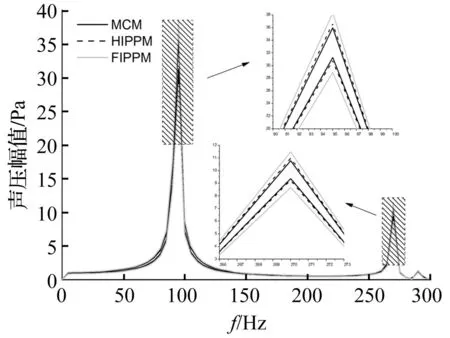
圖3 0~300 Hz頻域內聲壓幅值范圍 Fig.3 Bounds of the sound pressure amplitude in the frequency band 0~300 Hz
5結論
(1)兼顧系統自身參數及外載荷非概率不確定性,利用區間變量對不確定參數定量化,充分考慮彈性結構及內部聲場的耦合作用,建立含區間參數的結構-聲耦合系統動力學平衡方程;
(2)將區間攝動理論與有限元計算方法相結合,提出快速求解系統響應范圍的區間參數攝動分析方法。通過采用改進的Taylor展式及保留Neumann級數中的部分高階項,可有效提高計算精度;
(3)長方體密閉艙室模型計算結果表明,由于在系數矩陣求逆過程保留了Neumann級數的部分高階項,本文所建高階攝動方法所得較傳統一階攝動方法精度更高的聲壓范圍,可有效減少蒙特卡洛模擬帶來的計算耗費;
(4)本文研究的不確定數值計算方法不僅適用于聲場預測,亦為不確定結構靜/動力學響應分析提供新思路。
參考文獻
[1]陳馨蕊, 郝志勇, 楊陳, 等. 結構-聲耦合法在汽車儀表板隔聲性能仿真分析中的應用[J]. 振動與沖擊, 2009, 28(8): 154-157.
CHEN Xin-rui, HAO Zhi-yong, YANG Chen, et al. Simulation on sound insulation performance analysis of automotive dash by using structural-sound interaction method [J]. Journal of Vibration and Shock, 2009, 28(8): 154-157.
[2]Li S. A state-space coupling method for fluid-structure interaction analysis of plates [J]. Journal of the Acoustical Society of America, 2005, 118(2): 800-805.
[3]Raveendra S T. An efficient indirect boundary element technique for multi-frequency acoustic analysis [J]. International Journal for Numerical Methods in Engineering, 1999, 44(1): 59-76.
[4]James K R, Dowling D R. A probability the density function method for acoustic fielduncertainty analysis [J]. Journal of the Acoustical Society of America, 2005, 118(5): 2802-2810.
[5]Finette S. A stochastic response surface formulation of acoustic propagation through anuncertain ocean waveguide environment [J]. Journal of the Acoustical Society of America, 2009, 126(5): 2242-2247.
[6]Liu B S, Zhao G Z. PEM based sensitivity analysis for acoustic radiation problems of random responses [J]. Journal of Vibration and Acoustics, 2010,132(2): 0210121-02101211.
[7]王沖, 邱志平, 吳迪, 等. 結構-聲場耦合系統區間魯棒優化設計[J]. 振動與沖擊, 2013, 32(17): 8-13.
WANG Chong, QIU Zhi-ping, WU Di, et al. Interval robust optimization of a coupled structural-acoustic system [J]. Journal of Vibration and Shock, 2013, 32(17): 8-13.沖, 邱志平, 吳迪, 等. 結構-聲場耦合系統區間魯棒優化設計[J]. 振動與沖擊, 2013, 32(17): 8-13.
WANG Chong, QIU Zhi-ping, WU Di, et al. Interval robust optimization of a coupled structural-acoustic system [J]. Journal of Vibration and Shock, 2013, 32(17): 8-13.
[8]Edgecombe S, Linse P. Monte carlo simulation of two interpenetrating polymer networks: structure, swelling and mechanical properties [J]. Polymer, 2008, 49(7):1981-1992.
[9]Qiu Z P, Xia Y Y, Yang J. The static displacement and the stress analysis of structures with bounded uncertainties using the vertex solution theorem [J]. Computer Method in Applied Mechanics and Engineering, 2007, 196: 4965-4984.
[10]Qiu Z P, Chen S H, Elishakoff I. Bounds of eigenvalues for structures with an interval description of uncertain-but-non-random parameters [J]. Chaos Solitons & Fractals, 1996, 7(3): 425-434.
[11]Xia B Z, Yu D J, Liu J. Interval and subinterval perturbation methods for a structural-acoustic system with interval parameters [J]. Journal of Fluids and Structures, 2013, 38: 146-163.
[12]Chen S H, Ma L, Meng G W, et al. An efficient method for evaluating the natural frequency of structures with uncertain-but-bounded parameters [J]. Computers and Structures, 2009, 87(9/10):582-590.


