采用空間極化時(shí)頻分布的跳頻信號(hào)多參數(shù)聯(lián)合估計(jì)算法
張東偉,郭英,2,齊子森,張坤峰,張波,侯文林
(1.空軍工程大學(xué)信息與導(dǎo)航學(xué)院,710077,西安;2.通信網(wǎng)信息傳輸與分發(fā)技術(shù)重點(diǎn)實(shí)驗(yàn)室,050081,石家莊)
?
采用空間極化時(shí)頻分布的跳頻信號(hào)多參數(shù)聯(lián)合估計(jì)算法
張東偉1,郭英1,2,齊子森1,張坤峰1,張波1,侯文林1
(1.空軍工程大學(xué)信息與導(dǎo)航學(xué)院,710077,西安;2.通信網(wǎng)信息傳輸與分發(fā)技術(shù)重點(diǎn)實(shí)驗(yàn)室,050081,石家莊)
為了在欠定條件下利用信號(hào)二維波達(dá)方向(2D-DOA)與極化狀態(tài)進(jìn)行跳頻(FH)網(wǎng)臺(tái)分選和信號(hào)識(shí)別、跟蹤,提出了一種基于空間極化時(shí)頻分布(SPTFD)的FH信號(hào)多參數(shù)聯(lián)合估計(jì)算法。首先利用FH信號(hào)時(shí)頻域特征以及陣列流型建模方法,建立FH信號(hào)的極化敏感陣列快拍數(shù)據(jù)模型;然后通過(guò)組合時(shí)頻分布構(gòu)造各跳信號(hào)的SPTFD矩陣;在此基礎(chǔ)上,根據(jù)秩損理論對(duì)方向和極化信息進(jìn)行去耦合,利用旋轉(zhuǎn)不變子空間原理估計(jì)俯仰角;通過(guò)一維搜索和方程求解來(lái)估計(jì)方位角與極化參數(shù),最終實(shí)現(xiàn)了2D-DOA與極化參數(shù)的聯(lián)合估計(jì)。新算法無(wú)需多維參數(shù)尋優(yōu)和配對(duì),估計(jì)精度高。仿真結(jié)果表明:該算法能在欠定條件下精確估計(jì)FH信號(hào)2D-DOA和極化參數(shù);當(dāng)陣元數(shù)為4、信噪比大于6 dB時(shí),空間5個(gè)FH信號(hào)所有參數(shù)的均方根誤差均小于1°。
跳頻;極化;時(shí)頻分布;參數(shù)估計(jì)
跳頻(FH)通信因其優(yōu)越的抗干擾、抗截獲和多址組網(wǎng)等能力,已逐漸成為軍事通信的主導(dǎo)技術(shù)[1]。信號(hào)波達(dá)方向(DOA)和極化狀態(tài)在FH網(wǎng)臺(tái)分選、信號(hào)屬性識(shí)別、跟蹤和干擾等諸多任務(wù)中具有重要作用[2-8]。文獻(xiàn)[2-4]提出了基于空時(shí)數(shù)學(xué)模型的FH信號(hào)DOA估計(jì)方法,但要求信源數(shù)已知且小于陣元數(shù),不能用于欠定情況;文獻(xiàn)[5-7]基于空時(shí)頻處理思想,通過(guò)構(gòu)造FH信號(hào)各跳的時(shí)頻域協(xié)方差矩陣,利用子空間原理估計(jì)一維DOA,但未考慮2D-DOA問(wèn)題,無(wú)法定位三維空間目標(biāo)。
作為電磁波的重要屬性,極化增加了信息處理維度,結(jié)合信源方位能夠顯著提高FH信號(hào)辨識(shí)度[6]。同時(shí),極化信息的引入有利于提高陣列系統(tǒng)的DOA估計(jì)精度[9]。然而,目前關(guān)于FH信號(hào)DOA和極化聯(lián)合估計(jì)的研究成果非常少見(jiàn),可查資料中,僅文獻(xiàn)[8]有所涉及,但最多僅能處理5個(gè)信號(hào),限制了該算法的應(yīng)用范圍。因此,亟待尋求FH信號(hào)DOA和極化狀態(tài)的有效估計(jì)方法。此外,實(shí)際系統(tǒng)中陣元數(shù)受限,而空間信源數(shù)未知,特別是戰(zhàn)時(shí)FH組網(wǎng)密度高,易出現(xiàn)欠定情況。綜上所述,對(duì)于FH偵察,在欠定條件下開(kāi)展2D-DOA和極化參數(shù)的聯(lián)合估計(jì)具有重要理論價(jià)值和現(xiàn)實(shí)意義,但關(guān)于該問(wèn)題的研究鮮有報(bào)道。
本文通過(guò)引入空間極化時(shí)頻分布和秩損理論解決FH信號(hào)多參數(shù)聯(lián)合估計(jì)問(wèn)題。首先建立FH信號(hào)的極化敏感陣列快拍數(shù)據(jù)模型,同時(shí)采用一種新的組合時(shí)頻分布方法抑制FH交叉項(xiàng)以得到清晰穩(wěn)健的時(shí)頻圖,進(jìn)而選取各跳自項(xiàng)時(shí)頻點(diǎn)構(gòu)造其空間極化時(shí)頻分布(SPTFD)矩陣;在此基礎(chǔ)上,通過(guò)陣列流形形式變換結(jié)合秩損理論將方向和極化信息進(jìn)行去耦合,利用最小二乘ESPRIT原理估計(jì)俯仰角;通過(guò)一維角度搜索和方程求解估計(jì)方位角與極化參數(shù),最終實(shí)現(xiàn)了FH信號(hào)2D-DOA與極化參數(shù)的聯(lián)合估計(jì)。本文算法能用于欠定情況,且無(wú)需高維參數(shù)尋優(yōu)和配對(duì),在保證估計(jì)精度的前提下有效減小了計(jì)算復(fù)雜度。
1 FH信號(hào)的陣列快拍數(shù)據(jù)模型
設(shè)FH信號(hào)s(t)的跳周期為T(mén),在觀測(cè)時(shí)間內(nèi)共包含K跳,第k(k=1,…,K)跳的載頻為ωk,起始跳的持續(xù)時(shí)長(zhǎng)為Δt0,則s(t)可表示為[1]

(1)
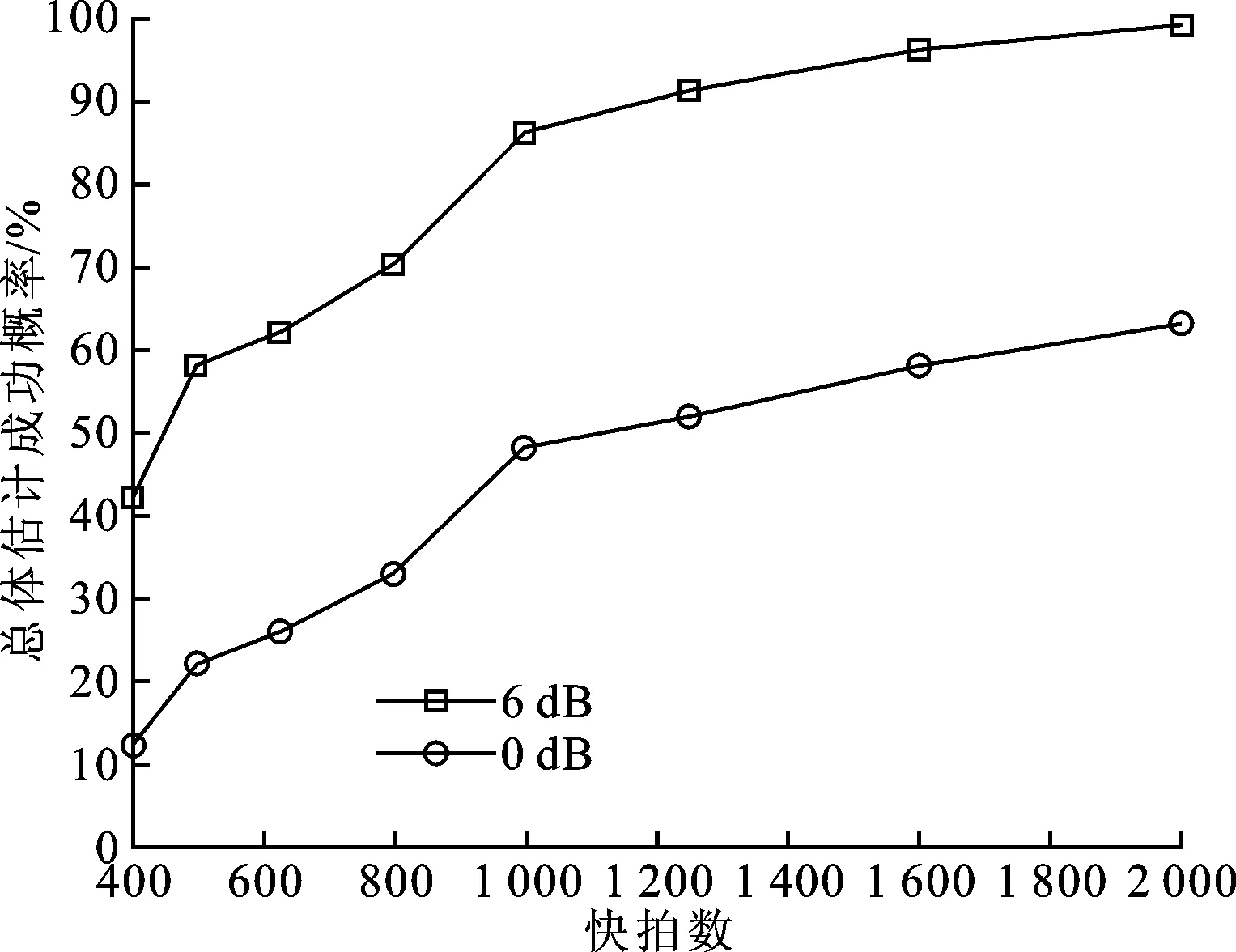
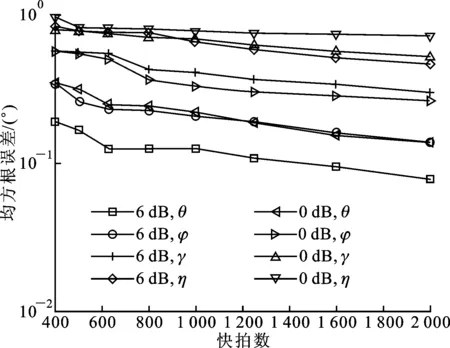
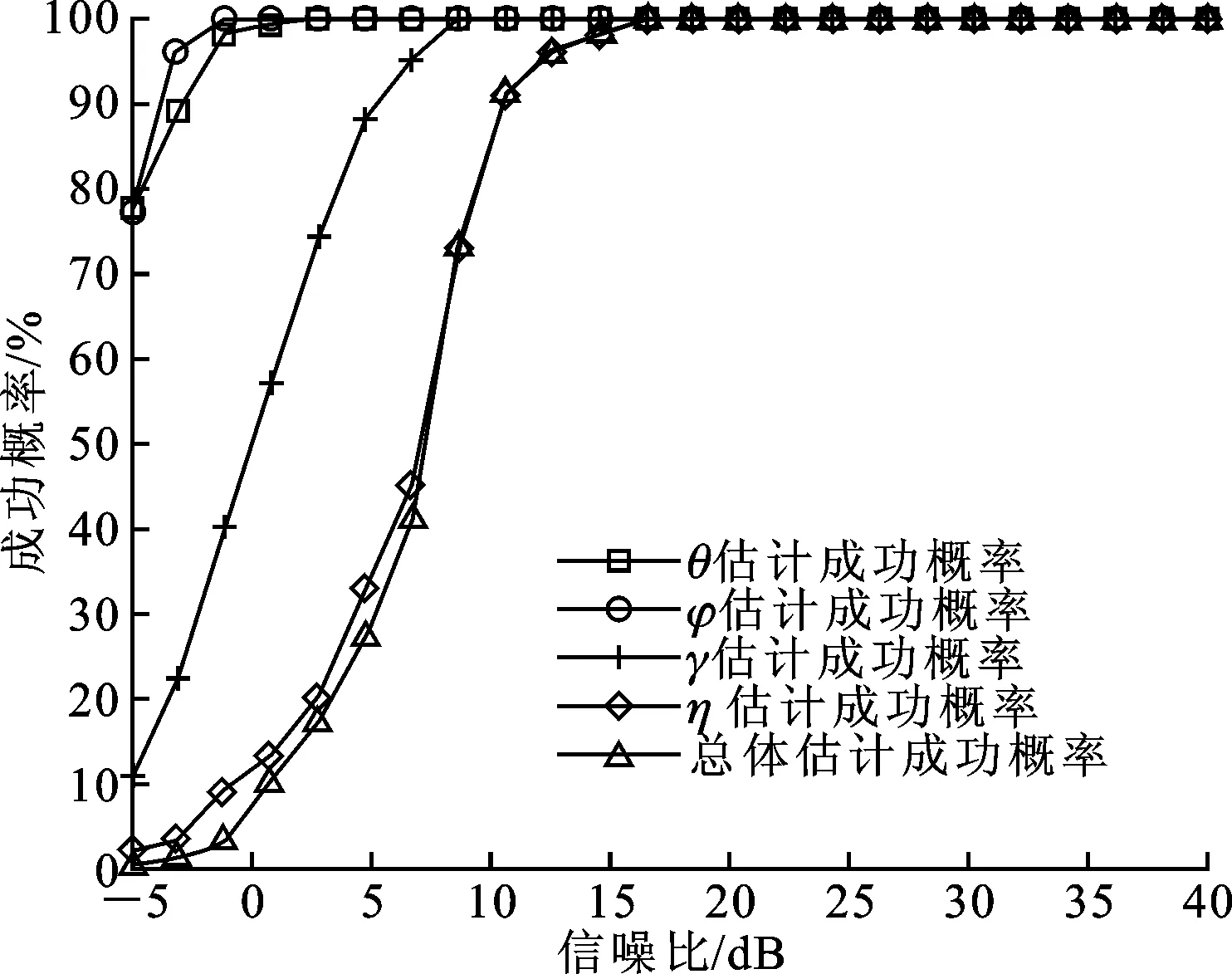
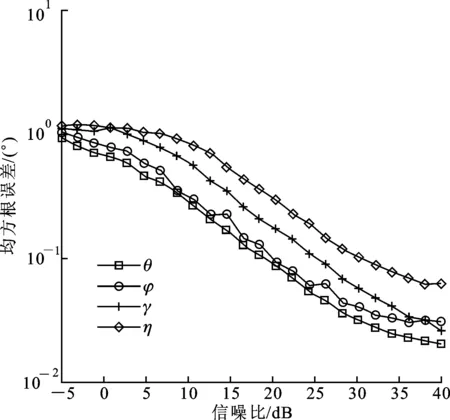
式中:t′=t-(k-1)T-Δt0;v(t)是s(t)的基帶復(fù)包絡(luò);φk是第k跳的初相;rect(t)為單位矩形窗。在空間直角坐標(biāo)系中分別沿X軸和Z軸方向構(gòu)造用正交電偶極子組成的均勻線陣,記為子陣1、子陣2。子陣1和子陣2的陣元數(shù)均為M,陣元間隔分別為d1、d2,并滿足max(d1,d2) 圖1 L型正交電偶極子陣列結(jié)構(gòu) 假設(shè)相位描述子為(γ,η)(γ∈[0,π/2]為極化輔角,η∈[0,2π]為極化相位差)的窄帶平面波S以俯仰角θ∈[0,π/2)和方位角φ∈[0,2π)沿單位方向-u入射,則極化矢量為[9] (2) 式中:γy、γz分別表示沿Y軸和Z軸方向的電場(chǎng)分量。假設(shè)陣列單元增益為1并忽略單陣元共點(diǎn)接收通道不一致及互耦影響,子陣1的導(dǎo)向矢量為 (3) 式中:p=e-(j2πd1sinθcosφ)/λ為相鄰陣元的相位差,λ=c/f(c為光速,f為載頻)為該跳信號(hào)波長(zhǎng);M為陣元數(shù);運(yùn)算符?為Kronecker積。同理,子陣2的導(dǎo)向矢量為 (4) 式中:q=e-(j2πd2cosθ)/λ。因此,陣列導(dǎo)向矢量為 (5) 當(dāng)空間存在N個(gè)信源s1~sN時(shí),陣列流型矩陣為 (6) 陣列的快拍數(shù)據(jù)矩陣為 (7) 式中:S(t)為信源的N×1維數(shù)據(jù)矢量;N(t)為陣列的4M×1維噪聲數(shù)據(jù)矢量。 構(gòu)造FH信號(hào)各跳的SPTFD矩陣是討論多參數(shù)聯(lián)合估計(jì)算法的基礎(chǔ)。下面首先簡(jiǎn)述SPTFD的基本原理,然后采取一種有效抑制交叉項(xiàng)的時(shí)頻分析方法得到清晰時(shí)頻圖以確定各跳自項(xiàng)區(qū)(用自項(xiàng)時(shí)頻點(diǎn)構(gòu)造SPTFD矩陣是算法性能正常發(fā)揮的前提),同時(shí)設(shè)計(jì)SPTFD矩陣的高效構(gòu)造策略。推導(dǎo)中假設(shè)噪聲為零均值且與信號(hào)不相關(guān)。 2.1 SPTFD的基本原理[10] SPTFD指將時(shí)頻分布擴(kuò)展至極化敏感陣列信號(hào),其突出優(yōu)勢(shì)是可實(shí)現(xiàn)信號(hào)的選擇性估計(jì),同時(shí)增加了極化域處理維度,利于提高DOA估計(jì)精度和獲取信源極化信息。對(duì)于信號(hào)x1(t)和x2(t),離散時(shí)間形式的Cohen類(lèi)互時(shí)頻分布為 (8) 式中:φ(l,τ)為核函數(shù)。SPTFD矩陣定義為 (9) (10) E[DXX(t,f)]與單極性陣列時(shí)域協(xié)方差模型Rxx=E[x(t)xH(t)]=ARssA+σ2IM具有類(lèi)似結(jié)構(gòu),且與A有相同的子空間特性。為確保E[DXX(t,f)]滿秩,通常選擇關(guān)注信號(hào)的多個(gè)自項(xiàng)時(shí)頻點(diǎn)采取聯(lián)合對(duì)角化或平均處理對(duì)其進(jìn)行估計(jì)。 2.2 組合時(shí)頻分布及SPTFD矩陣構(gòu)造策略 Wigner-Ville分布(WVD)的時(shí)頻聚焦性能最佳,但對(duì)多分量信號(hào)存在嚴(yán)重交叉項(xiàng)干擾且抗噪性能一般。平滑偽Wigner-Ville分布(SPWVD)經(jīng)過(guò)時(shí)、頻域2次平滑,在交叉項(xiàng)抑制、時(shí)頻聚焦性和抗噪能力這3個(gè)方面都取得了很好平衡。本文將WVD和SPWVD進(jìn)行組合,使兩者的優(yōu)勢(shì)均得以保留用于FH信號(hào)分析。SPWVD&WVD組合時(shí)頻分布的基本思想是:首先將SPWVD和WVD結(jié)果進(jìn)行點(diǎn)乘得到模具矩陣以抑制絕大部分交叉項(xiàng);再對(duì)模具矩陣進(jìn)行截?cái)嗵幚磉M(jìn)一步抑制噪聲,得到自項(xiàng)時(shí)頻地圖;最后將自項(xiàng)時(shí)頻地圖與SPWVD結(jié)果進(jìn)行點(diǎn)乘得到組合時(shí)頻分布。將參考陣元Z軸方向接收通道的SPWVD和WVD結(jié)果分別記為T(mén)SPWVD(t,f)和TWVD(t,f),自項(xiàng)時(shí)頻地圖記為MAU(t,f),有 (11) 式中:運(yùn)算符⊙表示Hadamard積;ξ為截?cái)嚅T(mén)限,ξ=μmean{|TSPWVD(t,f)⊙TWVD(t,f)|},其中μ為門(mén)限因子,mean{·}代表取均值。 圖2為3個(gè)FH信號(hào)的時(shí)頻分布結(jié)果。可見(jiàn),組合時(shí)頻分布沿襲了WVD的時(shí)頻聚焦性,交叉項(xiàng)和噪聲也消除殆盡。由于組合時(shí)頻分布確定的自項(xiàng)區(qū)域包含于SPWVD結(jié)果。因此,構(gòu)造SPTFD矩陣時(shí),組合時(shí)頻分布僅需作用于參考陣元以提供各跳信號(hào)時(shí)頻點(diǎn)選取范圍。為降低計(jì)算量,式(9)中Cohen分布可采用與SPWVD性能近似,計(jì)算量卻大為降低的SPW分布[6]。 (a)WVD (b)SPWVD (c)SPWVD&WVD組合圖2 多FH信號(hào)的3種時(shí)頻分布結(jié)果(RSN=5 dB) 3.1 信源方位和極化參數(shù)去耦合 對(duì)FH信號(hào)任意一跳,設(shè)其對(duì)應(yīng)的信源數(shù)為L(zhǎng),根據(jù)式(9)構(gòu)造SPTFD矩陣E{DXX(t,f)}|in并對(duì)其進(jìn)行特征分解得到噪聲子空間UN,根據(jù)子空間原理并考慮噪聲和有限快拍數(shù)影響,定義以下優(yōu)化問(wèn)題估計(jì)信源參數(shù) (12) (13) 式中:F(θ,φ)只包含由波程差導(dǎo)致的相位差;Y只包含極化參數(shù)。根據(jù)秩損理論[11],當(dāng)且僅當(dāng)(θ,φ)為真實(shí)方位時(shí),式(14)成立 (14) 由于Y不全為0,可通過(guò)二維搜索得到成對(duì)的俯仰角和方位角 (15) 式中:χmin[·]為求矩陣最小特征值算子。 3.2 俯仰角和方位角估計(jì) 根據(jù)式(15)估計(jì)方向角仍需二維搜索,下面尋找滿足旋轉(zhuǎn)不變關(guān)系的成對(duì)子陣,根據(jù)最小二乘ESPRIT原理對(duì)俯仰角進(jìn)行獨(dú)立估計(jì),從而避開(kāi)二維搜索,進(jìn)一步降低運(yùn)算量。設(shè)Aq1和Aq2分別為由A的第2M+1,2M+3,…,4M-1行和第2M+2,2M+4,…,4M行元素組成的子陣,則有 (16) (17) 式中:Yk,k=1,2,…,L為各信源對(duì)應(yīng)的極化矢量;qk=e-(j2πd2cosθk)/λin,k=1,2,…,L;Φq=diag[q1,q2,…,qL]。由式(16)和(17)可見(jiàn),Aq1和Aq2滿足旋轉(zhuǎn)不變關(guān)系,求得Φq對(duì)角元素即可解得俯仰角。假設(shè)E{DXX(t,f)}|in的信號(hào)子空間和噪聲子空間分別為Us、Un,由于span{Us}=span{A},按照由A構(gòu)成Aq1和Aq2的方式將Us劃分成2個(gè)分塊矩陣Us1和Us2,存在唯一的非奇異矩陣T滿足 (18) span(Aq1)=span(Us1)=span(Aq2)=span(Us2) (19) 所以,Us2=Us1T-1ΦqT=Us1Ψq,可見(jiàn)矩陣Ψq的特征值即為Φq對(duì)角元素qk,則俯仰角估計(jì)值為 (20) Ψq利用最小二乘ESPRIT算法[12]求得 (21) 將式(20)俯仰角估計(jì)值作為已知參數(shù)代入式(15),得方位角估計(jì)值 (22) 3.3 極化參數(shù)估計(jì) (23) 式中:emin[·]表示求矩陣最小特征值對(duì)應(yīng)的特征矢量算子。結(jié)合式(2),得極化比為 (24) 因此極化參數(shù)估計(jì)值為 (25) 式中 (26) 通過(guò)方位角、俯仰角與極化參數(shù)之間的解析關(guān)系式(13)、式(22)和式(23)可知,經(jīng)過(guò)上述處理過(guò)程,各參量實(shí)現(xiàn)了自動(dòng)配對(duì)。 3.4 性能分析 (1)只要各信號(hào)在時(shí)-頻域上存在差異,就可分別構(gòu)造其SPTFD矩陣,通過(guò)該算法估計(jì)各信號(hào)參數(shù),從而使陣列所能處理的FH信號(hào)總數(shù)不受陣元數(shù)限制。選取自項(xiàng)時(shí)頻點(diǎn)構(gòu)造SPTFD矩陣等價(jià)于進(jìn)行時(shí)頻域?yàn)V波,顯著提高了目標(biāo)信號(hào)信噪比,因此本文算法具有較強(qiáng)的信噪比適應(yīng)能力。 (2)俯仰角直接利用最小二乘ESPRRIT算法得到,影響估計(jì)精度的因素主要為噪聲;方位角基于俯仰角估計(jì)值,由一維角度搜索得到,誤差來(lái)源還包括俯仰角估計(jì)誤差和角度搜索步長(zhǎng);極化角則受俯仰角和方位角估計(jì)誤差的雙重影響。因此,同等條件下,俯仰角的估計(jì)性能最優(yōu),方位角次之,極化參數(shù)最差。 (3)陣元數(shù)增加時(shí),陣列孔徑增大;各跳信號(hào)的快拍數(shù)增加時(shí),構(gòu)造SPTFD矩陣可供利用的有效時(shí)頻點(diǎn)更多,有利于更充分的利用時(shí)頻信息和保證SPTFD矩陣的列滿秩;因此,算法性能隨著陣元數(shù)和快拍數(shù)的增加而提高。當(dāng)發(fā)生頻率碰撞時(shí)(對(duì)應(yīng)跳為多源估計(jì)問(wèn)題),由于信號(hào)間互擾的存在,導(dǎo)致算法估計(jì)性能差于無(wú)碰撞時(shí)。 3.5 本文算法步驟 根據(jù)以上推導(dǎo)和闡述,可得FH信號(hào)2D-DOA和極化參數(shù)聯(lián)合估計(jì)算法步驟如下: (1)對(duì)參考陣元數(shù)據(jù)進(jìn)行組合時(shí)頻分布,估計(jì)各跳持續(xù)時(shí)間、載頻和跳時(shí)刻[13],確定自項(xiàng)區(qū); (2)根據(jù)式(9)、(10)構(gòu)造某跳信號(hào)的SPTFD矩陣E[DXX(t,f)]|in,并對(duì)其進(jìn)行特征值分解; (3)估計(jì)該跳對(duì)應(yīng)的信源數(shù)L; (7)返回步驟(2)直至完成所有跳估計(jì)。 陣列結(jié)構(gòu)如圖1所示,2個(gè)子陣的陣元間距均為1.5 m;5個(gè)遠(yuǎn)場(chǎng)FH信號(hào)(FH1~FH5)參數(shù)分別為[20°,30°,40°,45°]、[30°,40°,50°,60°]、[40°,50°,60°,75°]、[50°,60°,75°,45°]、[60°,70°,35°,45°];角度搜索步長(zhǎng)0.05°;STFT平滑窗的采樣點(diǎn)數(shù)為335,SPWVD時(shí)域平滑窗的采樣點(diǎn)數(shù)為335,頻域平滑窗的采樣點(diǎn)數(shù)為101;構(gòu)造SPTFD矩陣時(shí)去除各跳首尾100個(gè)時(shí)頻點(diǎn)以避免平滑窗導(dǎo)致的相位模糊;截?cái)嘁蜃应倘?.1。均方根誤差(RMSE)定義為 (27) 實(shí)驗(yàn)1 暫無(wú)頻率碰撞,空間存在FH1、FH2和FH3,跳周期均為10 μs,采樣率100 MHz,采樣點(diǎn)數(shù)3 000;ULA陣元數(shù)M設(shè)為4,信噪比從-6 dB以2 dB間隔遞增到40 dB,各信噪比下進(jìn)行100次Monte-Carlo實(shí)驗(yàn)。圖3和圖4分別為(總體)估計(jì)成功概率(估計(jì)成功概率定義見(jiàn)文獻(xiàn)[11])及均方根誤差曲線。 圖3 實(shí)驗(yàn)1的估計(jì)成功概率 圖4 實(shí)驗(yàn)1各參數(shù)的均方根誤差曲線 實(shí)驗(yàn)結(jié)果表明,隨著信噪比的提高,各參數(shù)估計(jì)成功概率均逐漸增加:信噪比大于10 dB時(shí),總體估計(jì)成功概率逐漸接近100%;俯仰角和方位角的估計(jì)成功概率較高,基本保持在90%以上;極化參數(shù)性能略差,但當(dāng)信噪比大于8 dB時(shí)也達(dá)到90%以上。算法對(duì)方位角、俯仰角和極化角的RMSE值均較小,誤差水平滿足高分辨要求;俯仰角的估計(jì)精度最高,方位角次之,極化參數(shù)略差。 實(shí)驗(yàn)2 為驗(yàn)證陣元數(shù)對(duì)算法性能的影響,在信噪比分別取0 dB和6 dB時(shí),單臂ULA陣元數(shù)從4以2為間隔遞增到14,其余條件同實(shí)驗(yàn)1。 圖5 總體估計(jì)成功概率與陣元數(shù)的關(guān)系 圖5和圖6為算法性能與陣元數(shù)目的關(guān)系曲線。從圖5可見(jiàn),陣元數(shù)對(duì)本文算法性能具有較大影響:隨著陣元數(shù)增加,總體估計(jì)成功概率隨之提高(信噪比為6 dB,陣元數(shù)大于12時(shí)達(dá)到100%)。從圖6可以看出,各參數(shù)RMSE值隨陣元數(shù)的增加均逐步降低,但相比俯仰角和方位角,極化參數(shù)的RMSE曲線下降趨勢(shì)不明顯。 圖6 各參數(shù)RMSE與陣元數(shù)的關(guān)系 實(shí)驗(yàn)3 為驗(yàn)證快拍數(shù)對(duì)算法性能的影響,在信噪比分別取0 dB和6 dB時(shí),各跳快拍數(shù)從400漸增至2 000,其余條件同實(shí)驗(yàn)1(為保證公平,各FH信號(hào)均包含3跳進(jìn)行性能統(tǒng)計(jì)平均,因此各跳快拍數(shù)的變化體現(xiàn)為跳周期和采樣時(shí)長(zhǎng)的區(qū)別)。圖7和圖8為算法性能與快拍數(shù)的關(guān)系曲線。 圖7 總體估計(jì)成功概率與快拍數(shù)的關(guān)系 圖8 均方根誤差與快拍數(shù)的關(guān)系 圖7表明,總體估計(jì)成功概率隨著快拍數(shù)增加而提高,即跳周期越長(zhǎng)估計(jì)性能越好。圖8表明,各參數(shù)RMSE值隨快拍數(shù)的增加均逐步降低,但極化參數(shù)的RMSE性能差于俯仰角和方位角。 實(shí)驗(yàn)4 5個(gè)FH信號(hào)同時(shí)存在,為驗(yàn)證算法在欠定條件和頻率碰撞時(shí)的性能,設(shè)定兩信號(hào)間發(fā)生頻率碰撞的概率為1(每次實(shí)驗(yàn)隨機(jī)選擇一跳發(fā)生碰撞),3個(gè)信號(hào)以上的碰撞概率為0,其余條件與實(shí)驗(yàn)1相同。實(shí)驗(yàn)結(jié)果如圖9、圖10所示。 圖9 欠定條件和頻率碰撞時(shí)的估計(jì)成功概率 圖10 欠定條件和頻率碰撞時(shí)各參數(shù)的RMSE 圖9、圖10表明:在欠定條件和存在頻率碰撞時(shí),估計(jì)性能依然良好;信噪比大于14 dB時(shí),總體估計(jì)成功概率接近100%;信噪比大于6 dB時(shí)所有參數(shù)的RMSE均小于1度。頻率碰撞時(shí)相應(yīng)跳為多源估計(jì),因此對(duì)比圖9與圖3發(fā)現(xiàn),實(shí)驗(yàn)4的估計(jì)性能略差于實(shí)驗(yàn)1。本文實(shí)驗(yàn)設(shè)定的碰撞概率條件非常苛刻,已遠(yuǎn)超實(shí)際情況(通常兩電臺(tái)某跳發(fā)生頻率碰撞已屬小概率事件),證明在欠定條件和頻率碰撞時(shí)本文算法依然有效。 為了有效輔助FH網(wǎng)臺(tái)分選及信號(hào)識(shí)別、跟蹤,本文提出了基于空間極化時(shí)頻分布的FH信號(hào)二維波達(dá)方向與極化參數(shù)聯(lián)合估計(jì)算法。通過(guò)SPWVD & WVD組合時(shí)頻分布抑制交叉項(xiàng)和噪聲,確保利用自項(xiàng)時(shí)頻點(diǎn)構(gòu)造各跳信號(hào)的SPTFD矩陣,進(jìn)而根據(jù)秩損和子空間原理實(shí)現(xiàn)二維波達(dá)方向與極化參數(shù)的精確估計(jì)。仿真結(jié)果表明,在頻率碰撞和欠定條件下本文算法取得了優(yōu)良的參數(shù)估計(jì)性能,為欠定條件下跳頻通信偵察提供了新思路。 [1] FU K C, CHEN Y F. Blind iterative maximum likelihood-based frequency and transition time estimation for frequency hopping systems [J]. IET Communications, 2013, 7(9): 883-892. [2] LIU X Q, NICHOLAS D S, SWAMI A. Blind high-resolution localization and tracking of multiple frequency hopped signals [J]. IEEE Transactions on Signal Processing, 2002, 50(4): 889-901. [3] LIU X Q, NICHOLAS D S, SWAMI A. Joint hop timing and frequency estimation for collision resolution in FH networks [J]. IEEE Transactions on Wireless Communications, 2005, 4(6): 3063-3074. [4] LIN C H, FANG W H. Joint angle and delay estimation in frequency hopping systems [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1042-1056. [5] 陳利虎, 張爾揚(yáng). 基于數(shù)字信道化和空時(shí)頻分析的多跳頻信號(hào)DOA估計(jì) [J]. 通信學(xué)報(bào), 2009, 30(10): 68-74. CHEN Lihu, ZHANG Eryang. Directions of arrival estimation for multi frequency-hopping signals based on digital channelized receiver and spatial time-frequency analysis [J]. Journal of Communications, 2009, 30(10): 68-74. [6] 陳利虎. 跳頻信號(hào)的偵察技術(shù)研究 [D]. 長(zhǎng)沙: 國(guó)防科學(xué)技術(shù)大學(xué), 2009. [7] 王永明, 王世練, 張爾揚(yáng). 多跳頻脈沖的高效測(cè)向算法 [J]. 哈爾濱工程大學(xué)學(xué)報(bào), 2011, 32(5): 662-666. WANG Yongming, WANG Shilian, ZHANG Eryang. An effective direction finding method for multi-frequency hopping pulses [J]. Journal of Harbin Engineering University, 2011, 32(5): 662-666. [8] WONG K T. Blind beamforming/geolocation for wide-band FFHs with unknown hop-sequences [J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 65-76. [9] 莊釗文, 徐振海, 肖順平, 等. 極化敏感陣列信號(hào)處理 [M]. 北京: 國(guó)防工業(yè)出版社, 2005: 199-212. [10]ZHANG Y M, OBEIDAT B A, AMIN M G. Spatial polarimetric time frequency distribution for direction of arrival estimation [J]. IEEE Transactions on Signal Processing, 2006, 54(4): 1327-1340. [11]齊子森, 郭英, 王布宏, 等. 共型陣列天線信源方位與極化狀態(tài)的聯(lián)合估計(jì)算法 [J]. 電子學(xué)報(bào), 2012, 40(12): 2562-2566. QI Zisen, GUO Ying, WANG Buhong, et al. Joint DOA and polarization estimation algorithm for conformal array antenna [J]. Acta Electronica Sinica, 2012, 40(12): 2562-2566. [12]王永良, 陳輝, 彭應(yīng)寧, 等. 空間譜估計(jì)理論與算法 [M]. 北京: 清華大學(xué)出版社, 2004: 185-211. [13]付衛(wèi)紅, 王璐, 賈坤, 等. 基于STFT與SPWVD的跳頻參數(shù)盲估計(jì)算法 [J]. 華中科技大學(xué)學(xué)報(bào): 自然科學(xué)版, 2014, 42(9): 59-63. FU Weihong, WANG Lu, JIA Kun, et al. Blind parameter estimation for frequency hopping signals based on STFT and SPWVD [J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2014, 42(9): 59-63. [本刊相關(guān)文獻(xiàn)鏈接] 尚佳棟,王祖林,周麗娜,等.采用隨機(jī)共振增強(qiáng)的混合擴(kuò)頻信號(hào)跳頻參數(shù)估計(jì).2014,48(10):42-48.[doi:10.7652/xjtuxb201410007] 鄭紀(jì)彬,任愛(ài)鋒,蘇濤,等.多分量Chirp信號(hào)相位參數(shù)的精確估計(jì)算法.2013,47(2):69-74.[doi:10.7652/xjtuxb201302 012] 王云龍,吳瑛.聯(lián)合時(shí)延與多普勒頻率的直接定位改進(jìn)算法.2015,49(4):123-129.[doi:10.7652/xjtuxb201504020] 熊濤,江樺,崔鵬輝,等.應(yīng)用基擴(kuò)展模型的混合信號(hào)單通道盲分離算法.2015,49(6):60-66.[doi:10.7652/xjtuxb201506 010] (編輯 劉楊) A Joint Estimation Algorithm of Multiple Parameters for Frequency Hopping Signals Using Spatial Polarimetric Time Frequency Distributions ZHANG Dongwei1,GUO Ying1,2,QI Zisen1,ZHANG Kunfeng1,ZHANG Bo1,HOU Wenlin1 (1. School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China; 2. Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China) A novel multi-parameter joint estimation algorithm based on spatial polarimetric time-frequency distributions (SPTFD) for frequency-hopping (FH) signals is proposed to sort frequency-hopping network, identifying and to track signals effectively via the two dimensional direction of arrival (2D-DOA) and polarization of FH signals in underdetermined conditions. Both the time and the frequency features of FH signals are used to derive a data model for its polarization sensitive array based on the modeling method for manifold matrices of arrays; Then a SPTFD matrix for each hop is generated by the combined time-frequency distribution. The 2D-DOA and the polarization information are then de-coupled in the light of rank reduction theory, and the elevation angle is estimated via ESPRIT algorithm. Both the azimuth and the polarization are estimated through one-dimensional search and equation solution, respectively, and the joint estimation of both the 2D-DOA and the polarization of FH signals is completed. The proposed algorithm has good estimate precision without multi parameters optimization or pair-matching. Simulation results show that the proposed algorithm accurately estimates the 2D-DOA and the polarization of FH signals in underdetermined conditions and that the RMSE of all parameters for five FH signals is less than one degree when there are 4 sensors and the SNR is bigger than 6 dB. frequency hopping; polarization; time-frequency distribution; parameter estimation 2014-11-26。 作者簡(jiǎn)介:張東偉(1987—),男,博士生;郭英(通信作者),女,教授,博士生導(dǎo)師。 基金項(xiàng)目:國(guó)家自然科學(xué)基金資助項(xiàng)目(61072148);通信網(wǎng)信息傳輸與分發(fā)技術(shù)重點(diǎn)實(shí)驗(yàn)室基金資助項(xiàng)目(ITD-U12003/K1260009)。 時(shí)間:2015-05-15 10.7652/xjtuxb201508004 TN911.7 A 0253-987X(2015)08-0017-07 網(wǎng)絡(luò)出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150515.1747.003.html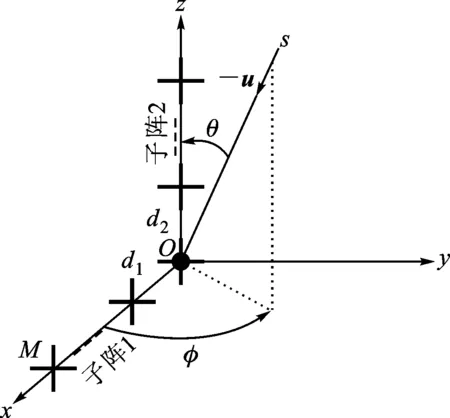
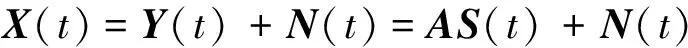
2 FH信號(hào)的SPTFD矩陣構(gòu)造
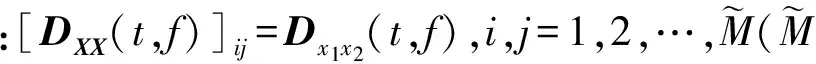

3 2D-DOA與極化參數(shù)聯(lián)合估計(jì)
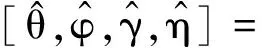
4 仿真結(jié)果與分析
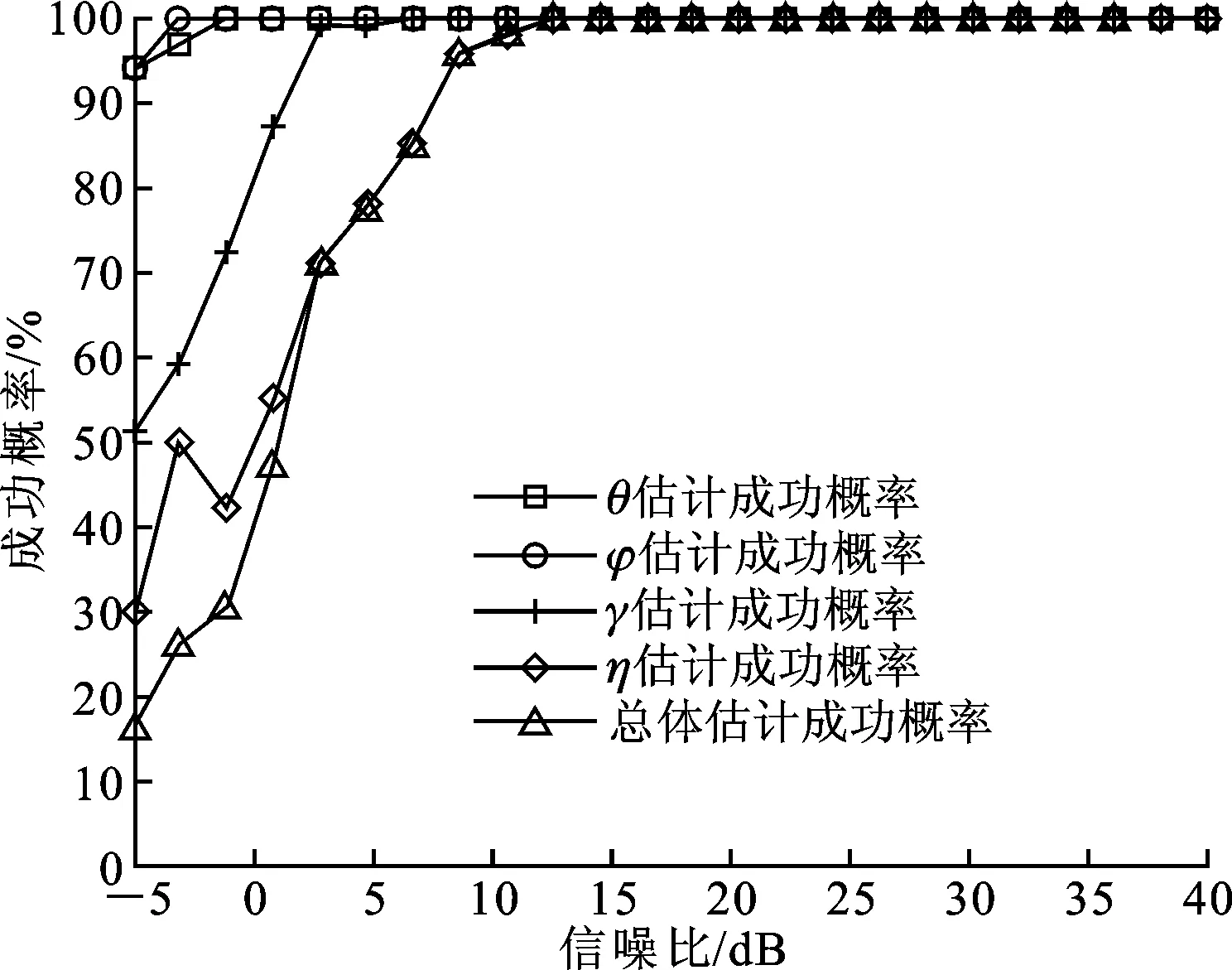
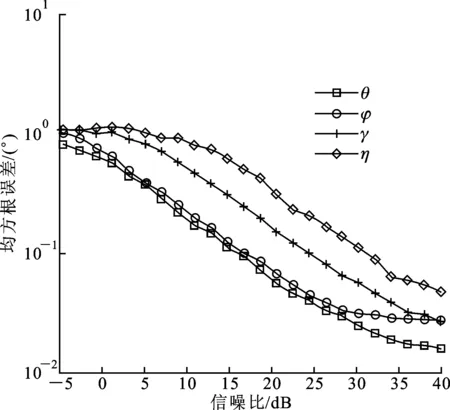
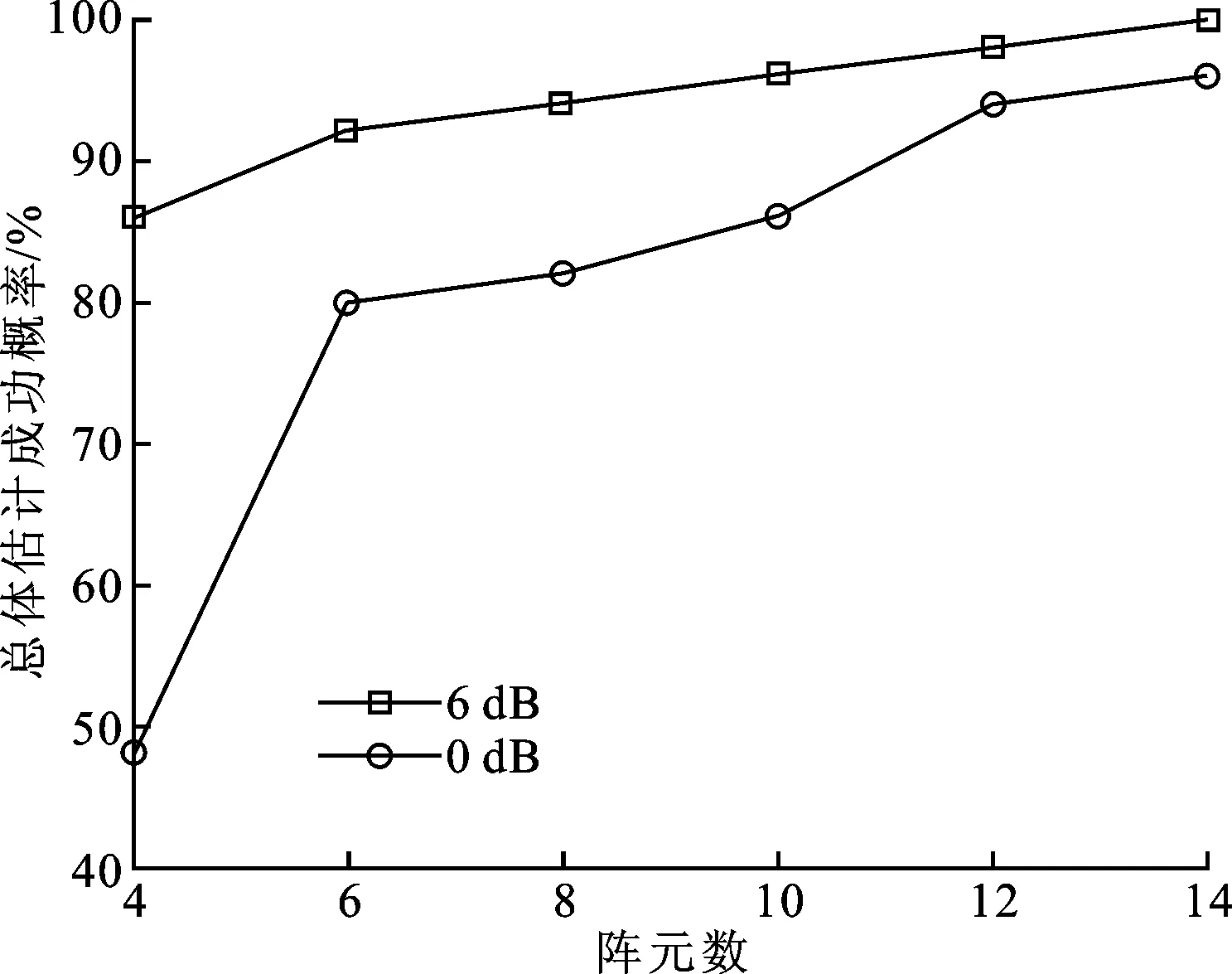
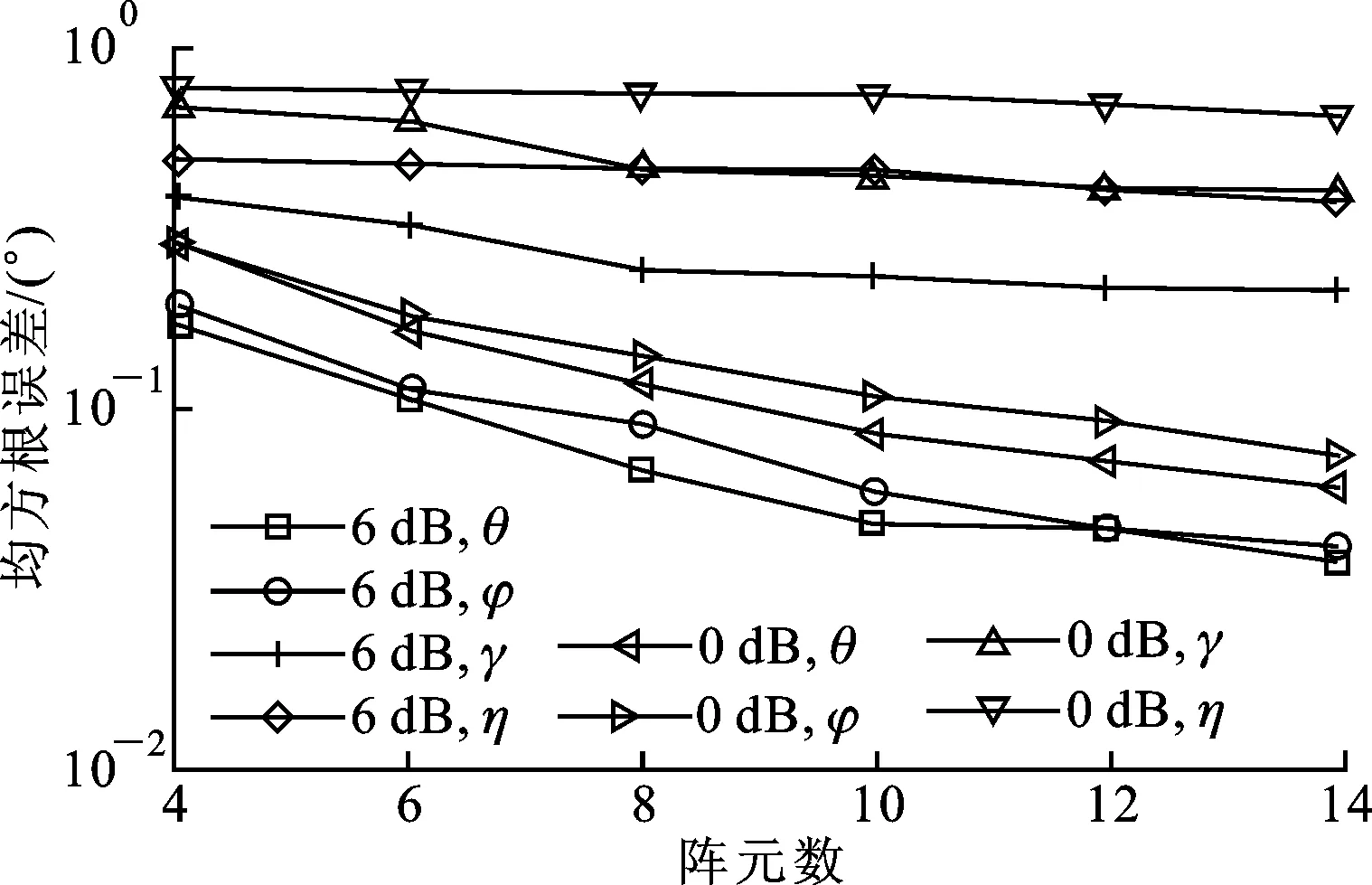
5 結(jié) 論

