拓展目標雜波概率假設密度估計

閆小喜,韓崇昭,李威,連峰

(1.江蘇大學電氣信息工程學院,212013,江蘇鎮江;2.西安交通大學電子與信息工程學院,710049,西安)

?

拓展目標雜波概率假設密度估計

閆小喜1,韓崇昭2,李威2,連峰2

(1.江蘇大學電氣信息工程學院,212013,江蘇鎮江;2.西安交通大學電子與信息工程學院,710049,西安)

針對拓展目標概率假設密度濾波器中的未知雜波概率假設密度,提出了雜波概率假設密度估計算法。算法利用有限混合模型極大后驗估計雜波概率假設密度,取混合權重的熵分布作為混合參數的先驗分布;在漸進假設條件下,利用拉格朗日乘子推導了混合權重的遞進估計公式;在混合權重遞進估計過程中,通過混合權重置零操作來實現對有限混合模型中混合分量的刪減。以二維場景為例對算法進行了仿真實驗,結果表明:在拓展目標概率假設密度濾波器高斯混合實現的框架內,所提雜波概率假設密度估計算法的跟蹤性能接近真實雜波概率假設密度時的跟蹤性能。

拓展目標跟蹤;雜波概率假設密度;極大后驗;熵分布

目標跟蹤是對目標數目和目標狀態進行估計。目前已有的目標跟蹤算法大部分是基于這樣一個基本假設:每個目標在每個時刻至多產生一個量測[1-3]。在一般分辨率目標跟蹤系統中,目標尺寸相對于傳感器分辨單元可以忽略不計,目標能夠簡化為一個點目標,一個點目標對應一個散射中心,“單散射中心”特征體現在量測上為“一個目標對應一個量測”,又考慮到傳感器檢測概率的因素,因此每個目標在每個時刻至多產生一個量測,該假設具有一定的合理性。

然而,隨著現代傳感器分辨率的不斷提高,尤其以高分辨率雷達、相控陣雷達為代表的現代傳感器的出現,“每個目標在每個時刻至多產生一個量測”的基本假設越來越不適用于現代高分辨率目標跟蹤系統,因為在高分辨率目標跟蹤系統中,目標尺寸一般大于傳感器距離向分辨單元,每個目標具有多個散射中心,該“多散射中心”特征體現在量測上為“每個目標在每個時刻產生多個目標量測”。因此,在現代目標跟蹤系統,目標跟蹤應當是基于“每個目標在每個時刻產生多個量測”的拓展目標跟蹤而非點目標跟蹤[4]。目前關于拓展目標跟蹤的研究主要集中在特定約束條件下的單拓展目標跟蹤,如基于參考框架的單拓展目標序貫蒙特卡羅方法[5]、基于狀態擴維的單拓展目標序貫蒙特卡羅方法[6]、隨機矩陣描述的拓展目標跟蹤方法[7]、基于泊松一致性似然的單拓展目標Bayesian方法[8]、單拓展目標的聯合檢測和估計誤差[9]等。有關多拓展目標跟蹤的研究較少,比較嚴謹的理論是Mahler在多目標Bayesian濾波器框架內利用隨機有限集統計所推導的多拓展目標概率假設密度濾波器[10],該濾波器在拓展目標線性高斯假設條件下,具有線性高斯混合實現形式,能夠實現對多拓展目標狀態的估計[11-12]。拓展目標概率假設密度濾波器高斯混合實現的收斂性在文獻[13]中進行了證明。

在拓展目標概率假設密度濾波器中,雜波概率假設密度作為拓展目標概率假設密度的重要組成部分,在實際跟蹤系統中是未知的。然而,在已有的大部分拓展目標跟蹤算法中,粗略地強制指定雜波概率假設密度,其描述的精確與否在一定程度上影響到拓展目標概率假設密度濾波器的跟蹤性能。針對拓展目標概率假設密度濾波器中的未知雜波概率假設密度,本文提出了雜波概率假設密度估計算法,此算法能提高拓展目標概率假設密度濾波器的適用性。

1 問題描述

拓展目標概率假設密度濾波器的預測步為

(1)

式中:vk|k-1是拓展目標強度;pS,k是存活概率;fk|k-1是狀態轉移密度;βk|k-1是衍生轉移密度;γk是拓展目標出生強度[10]。

拓展目標概率假設密度濾波器更新步[10]為

vk|k(x)=LZk(x)vk|k-1(x)

(2)

偽量測似然

(3)

式中:λ(x)是期望目標量測數;PD是檢測概率;p∠Zk表示對量測集合Zk的分割;ωp是分割方式p在所有可能分割方式中所占的比重;W是量測分割單元;|W|表示分割單元W中量測數目;φz(x)=φ(z|x)是量測似然;λc是期望雜波數;ck(z)是雜波分布;分割單元因子

dW=δ|W|,1+

(4)

其中δ是Kronecker delta函數。

雙重強度函數定義為

(5)

式(3)中的1-(1-e-λ(x))PD(x)表示對未檢測到預測步拓展目標概率假設密度的保留,其余部分項表示對檢測到預測拓展目標概率假設密度的更新。

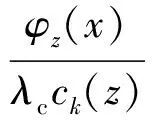
(6)

式中:λ(x)φz(x)表示z作為目標量測時的目標量測強度;λcck(z)表示z作為雜波量測時的雜波量測強度。該比率值R是利用當前量測更新檢測到預測拓展目標概率假設密度的關鍵,R作為更新因子能夠體現出量測集合中量測的更新作用。在實際跟蹤系統中,λ(x)、φz(x)與跟蹤系統所選的傳感器有關,可以視為已知量;表示雜波概率假設密度的參數λc、ck(z)與跟蹤場景有關,是未知量。針對該未知的雜波概率假設密度,本文提出了拓展目標雜波概率假設密度估計算法,該算法可提高拓展目標概率假設密度濾波器在更新步的更新精度。

2 算 法

如問題描述部分所述,我們的目的是對未知的雜波概率假設密度進行估計,其中包括對期望雜波量測數目λc和雜波分布ck(z)的估計。

關于λc的估計,前k-1時刻雜波數目估計值的平均值作為k時刻雜波數目的估計值,即

(7)

算法利用有限混合模型對未知的c(z)進行估計(為表述簡單,省略時刻標注k)

(8)

式中:m是混合分量數;πj是混合分量權重;θ是由均值μj、方差Pj構成的描述分量j的參數集合,θ={π1,…,πm,θ1,…,θm}。雜波量測集合Zc={z1,…,zn}的對數似然為

(9)

算法采用極大后驗準則估計混合參數為

(10)

該混合參數的先驗分布依賴于混合權重的熵分布[14],即

p(θ)∝exp(-H(π1,…,πm))

(11)

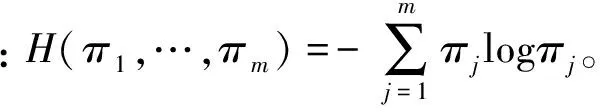
求πj在雜波量測集合Zc,i-1={z1,…,zi-1}下的極大后驗估計時,令

(12)

(13)

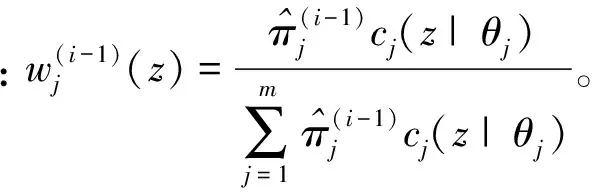
(14)

(15)

將式(13)、式(15)代入到式(14),可得混合權重的遞進估計關系為

(16)

式中

式(16)是超越方程,利用Lambert W函數[15]求解該方程得

(17)

在上述遞進估計過程中,如果某一混合分量的混合權重為負值,則令該混合權重為0,使該混合分量不出現在對數后驗密度的計算中,從而實現對該混合分量的刪減,而且該混合分量不再出現在后續估計過程中。在混合權重的遞進估計過程中,對非零混合權重所對應的混合分量的均值、方差采用文獻[16]的遞進估計方式進行。

3 仿真實驗

以二維場景[-1 000,1 000]×[-1 000,1 000]為例,在拓展目標概率假設密度濾波器高斯混合實現框架內,證明所提算法在拓展目標跟蹤上的有效性。拓展目標運動模型為

式中:xk=[x1,k,x2,k,x3,k,x4,k]T為拓展目標狀態;[x1,k,x2,k]T為拓展目標位置;[x3,k,x4,k]T為拓展目標速度;過程噪聲[v1,k,v2,k]T是零均值高斯白噪聲,其分量標準差σv1=σv2=2 m/s2。拓展目標存活概率為0.99,拓展目標出生強度γk由兩個加權高斯混合分量來表示,其中一個分量的參數權重為0.1、均值為[250,250,0,0]T、方差為diag([900,900,25,25]T);另一個分量的參數權重為0.1、均值為[-250,-250,0,0]T、方差為diag([900,900,25,25]T)。拓展目標衍生強度βk|k-1(x|ζ)=0.05N(x,ζ,Qβ),其中衍生方差陣Qβ=diag([100,100,400,400]T),原狀態ζ到衍生狀態x的衍生轉移矩陣Fβ=diag([1,1,1,1]T),ζ到x的狀態跳躍dβ=[0,0,0,0]T。

拓展目標單量測方程為

式中:量測噪聲[w1,k,w2,k]T是零均值高斯白噪聲,其分量標準差σw1=σw2=20 m。每個拓展目標在每個時刻產生的量測數服從參數為10的泊松分布,檢測概率為0.99。

算法在有限混合模型初始化時,取混合分量數為50,算法的混合參數遞進估計過程終止條件為對數后驗密度的相對變化率低于10-4。算法在拓展目標概率假設密度濾波器高斯混合實現框架內進行驗證,其參數設置與文獻[11]相同。

拓展目標在一次蒙特卡羅實驗中的x坐標和y坐標上的真實狀態和目標量測如圖1、圖2所示,可以看出拓展目標的多量測特性。

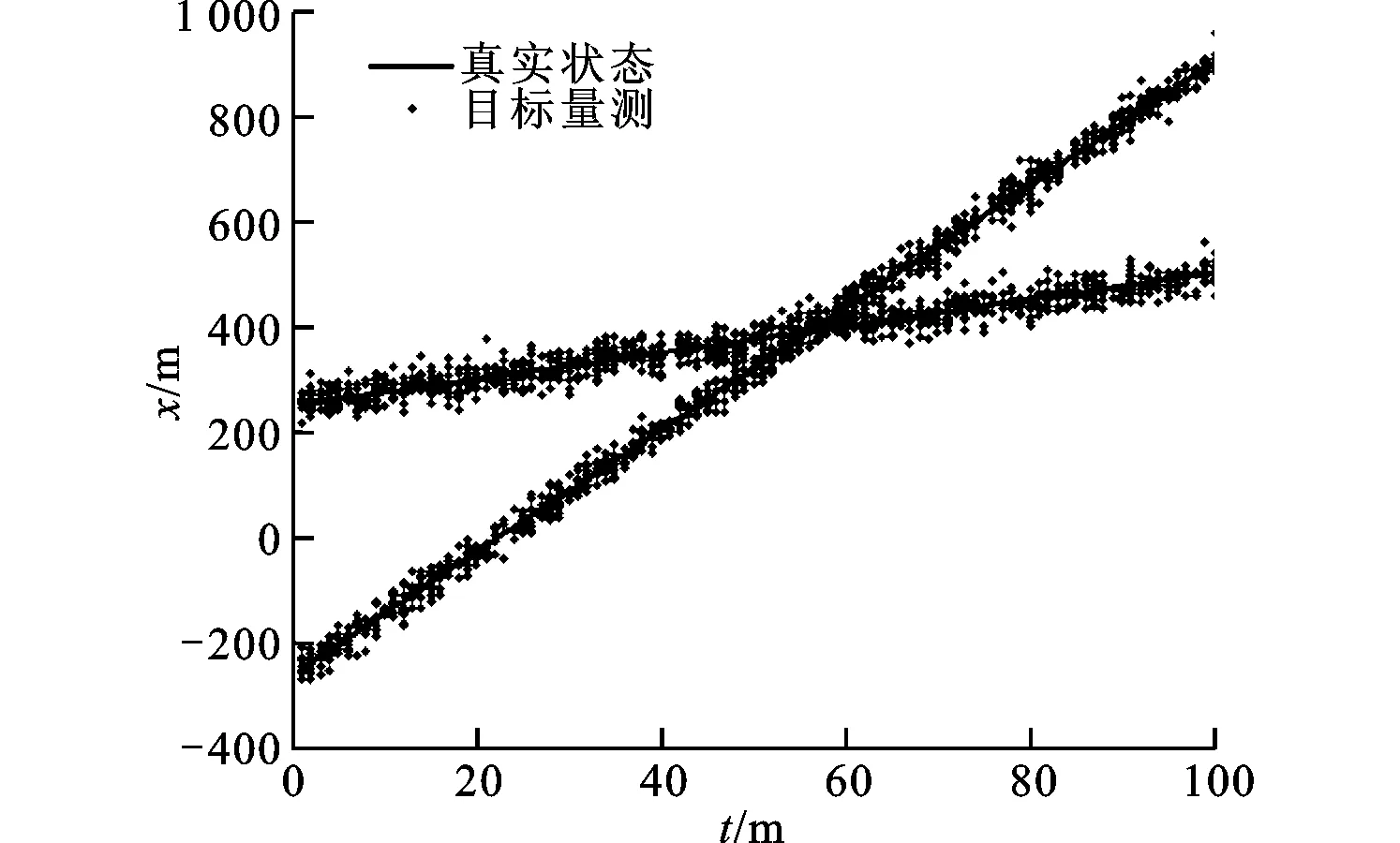
圖1 x坐標的真實狀態與目標量測

圖2 y坐標的真實狀態與目標量測

拓展目標真實軌跡和所提算法估計值如圖3、圖4所示。結果表明,所提算法在拓展目標概率假設密度濾波器高斯混合實現框架中能夠實現對多拓展目標狀態的有效估計。

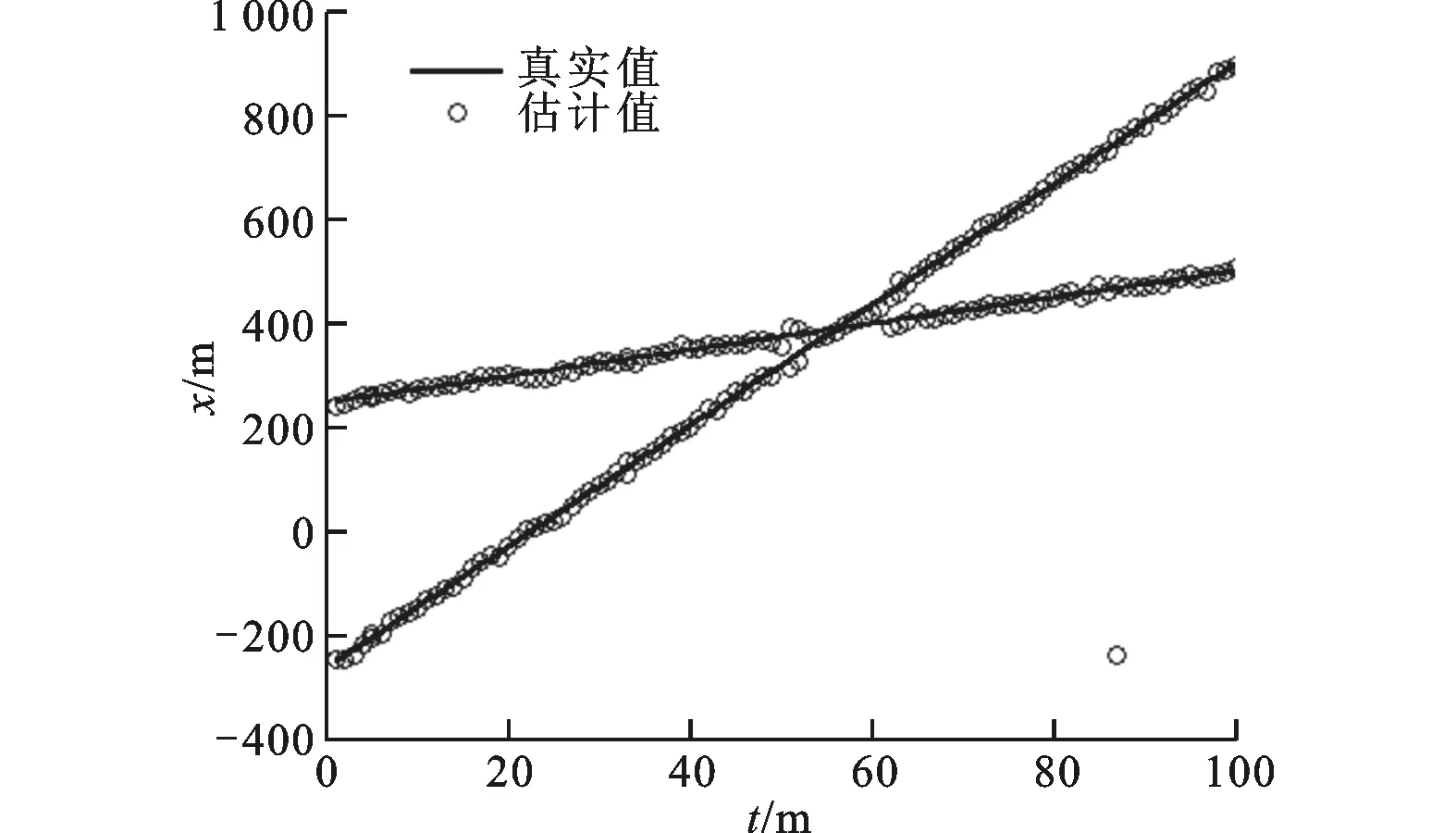
圖3 x坐標的估計值與真實值

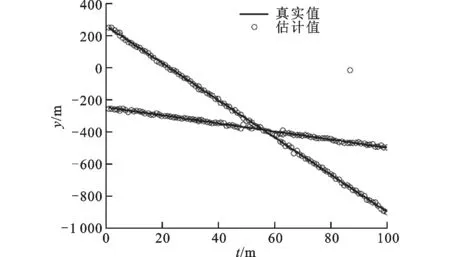
圖4 y坐標的估計值與真實值

所提算法與使用真實雜波概率假設密度時的拓展目標數目估計效果如圖6所示,可以看出,所提算法的目標數估計值在大多數時刻接近于真實雜波概率假設密度時的目標數估計值。

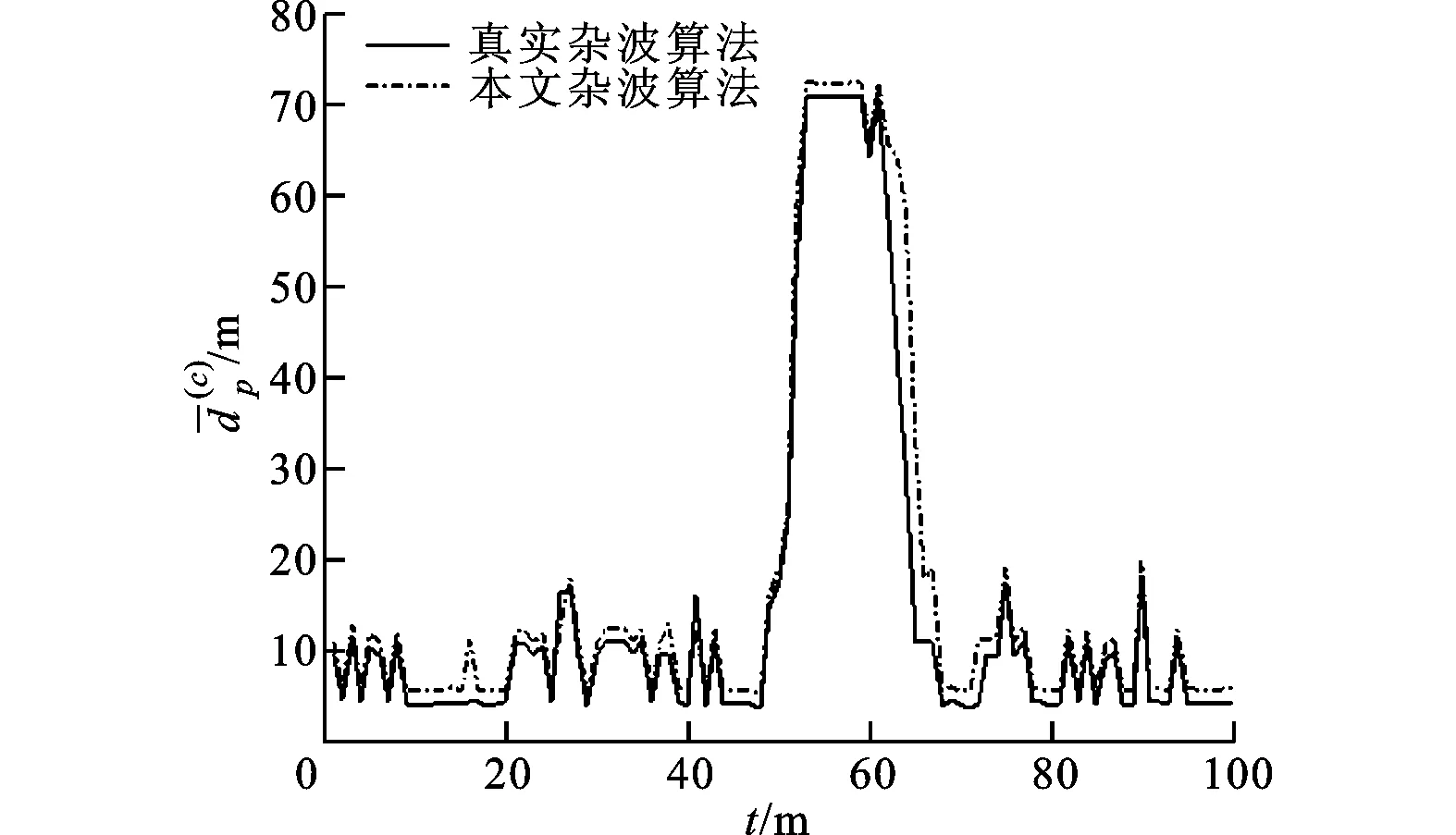
圖5 平均OSPA

圖6 平均目標數目

4 結 論

作為拓展目標概率假設密度濾波器強度更新因子中重要組成部分的雜波概率假設密度,在實際目標跟蹤系統中是未知的。針對該未知雜波概率假設密度,本文提出了雜波概率假設密度的估計算法,算法利用有限混合模型實現對雜波概率假設密度的遞進估計。仿真結果表明:所提算法能夠實現對雜波概率假設密度的估計,跟蹤性能接近真實雜波概率假設密度時的跟蹤性能。

[1] PULFORD G E. Taxonomy of multiple target tracking methods [J]. IET Proceeding of Radar, Sonar and Navigation, 2005, 152(2): 291-304.

[2] BLACKMAN S, POPOLI R. Design and analysis of modern tracking systems [M]. Norwood, USA: Artech House, 1999.

[3] BAR S Y, LI Xiaorong. Multitarget-multisensor tracking: principles and techniques [M]. Storrs, USA: YBS Publishing, 1995.

[4] GILHOLM K, SALMOND D. Spatial distribution for tracking extended objects [J]. IEEE Proceedings of Radar, Sonar and Navigation, 2005, 152(5): 364-371.

[5] VERMAAK J, IKOMA N, GODSILL S J. Sequential Monte Carlo framework for extended object tracking [J]. IEEE Proceedings of Radar, Sonar and Navigation, 2005, 152(3): 353-363.

[6] ANGELOVA D, MIHAYLOYA L. Extended object tracking using Monte Carlo methods [J]. IEEE Transactions on Signal Processing, 2008, 56(2): 825-832.

[7] KOCH J W. Bayesian approach to extended object and cluster tracing using random matrices [J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059.

[8] VO B T, VO B N, CANTONI A. Bayesian filtering with random finite set observations [J]. IEEE Transactions on Signal Processing, 2008, 56(4): 1313-1326.

[9] 連峰, 馬東東, 韓崇昭. 擴展目標聯合檢測與估計的誤差界 [J]. 西安交通大學學報, 2014, 48(4): 8-14. LIAN Feng, MA Dongdong, HAN Chongzhao. Error bound for joint detection and estimation for extended target [J]. Journal of Xi’an Jiaotong University, 2014, 48(4): 8-14.

[10]MAHLER R. PHD filters for nonstandard targets: I extended object [C]∥The 12th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2009: 915-921.

[11]GRANSTROM K, LUNDQUIST C, ORGUNER O. Extended target tracking using a Gaussian-mixture PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.

[12]韓玉蘭, 朱洪艷, 韓崇昭, 等. 多拓展目標的高斯混合概率假設密度濾波器 [J]. 西安交通大學學報, 2014, 48(4): 95-101. HAN Yulan, ZHU Hongyan, HAN Chongzhao, et al. Gaussian-mixture probability hypothesis density filter for multiple extended targets [J]. Journal of Xi’an Jiaotong University, 2014, 48(4): 95-101.

[13]連峰, 韓崇昭, 劉偉峰, 等. 高斯混合擴展目標概率假設密度濾波器的收斂性分析 [J]. 自動化學報, 2012, 38(8): 1343-1352.

LIAN Feng, HAN Chongzhao, LIU Weifeng, et al. Convergence analysis of the Gaussian mixture extended-target probability hypothesis density filter [J]. Acta Automatica Sinca, 2012, 38(8): 1343-1352.

[14]吳剛, 韓崇昭, 閆小喜, 等. 基于熵分布的概率假設密度濾波器高斯混合實現 [J]. 控制與決策, 2014, 29(1): 89-93. WU Gang, HAN Chongzhao, YAN Xiaoxi, et al. Gaussian mixture implementation of PHD filter based on entropy distribution [J]. Control and Decision, 2014, 29(1): 89-93.

[15]CORLESS R M, GONNET G H, HARE D, et al. On the Lambert W function [J]. Advances in Computational Mathematics, 1996, 5(4): 329-359.

[16]ZIVKOVIC Z, HEIJDEN F V. Recursive unsupervised learning of finite mixture models [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(5): 651-656.

[17]SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filters [J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.

(編輯 趙煒)

Estimation of Clutter Probability Hypothesis Density in Extended Objects

YAN Xiaoxi1,HAN Chongzhao2,LI Wei2,LIAN Feng2

(1. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013, China; 2. School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

An algorithm to estimate the clutter probability hypothesis density is proposed to deal with unknown clutter probability hypothesis densities in extended object probability hypothesis density filter. A finite mixture model is applied in estimating clutter probability hypothesis density with maximum a posterior estimation, and the entropy distribution of mixed weights is regarded as the prior distribution of mixing parameters. A recursive estimation formula of mixed weights is derived by using Lagrange multiplier under an approximation assumption. Mixture components of the finite mixture model are pruned by setting corresponding mixed weights to zeros in the recursive estimation procedure. Simulation results in a two-dimensional scenario show that the tracking performance of the proposed algorithm is close to the ground truth in Gaussian mixture implementation of extended object probability hypothesis density filter.

extended object tracking; clutter probability hypothesis density; maximum a posterior; entropy distribution

2014-04-18。

閆小喜(1981—),男,博士,講師。

國家自然科學基金資助項目(61304261);江蘇大學高級人才啟動基金資助項目(12JDG076)。

10.7652/xjtuxb201501015

TP274

A

0253-987X(2015)01-0092-05