譜元方法求解對流擴散方程及其穩定性分析

和文強,秦國良

(西安交通大學流體機械研究所,710049,西安)

?

譜元方法求解對流擴散方程及其穩定性分析

和文強,秦國良

(西安交通大學流體機械研究所,710049,西安)

探討了一維對流擴散方程的一種高精度數值解法,該解法在空間上采用了Chebyshev譜元方法,在時間上結合了半隱式Adams方法。通過數值算例驗證了解法的可行性,利用特征分析法得到了對流擴散方程譜元求解時不同離散形式的穩定性條件,并對數值求解的穩定性進行了預測。通過時間步長、網格劃分、對流項和黏性項插值階數的影響研究表明:耦合Chebyshev譜元方法和半隱式Adams方法在求解對流擴散方程時能夠獲得高精度的數值解;時間離散時Adams方法的黏性項采用一階插值形式、對流項采用二階插值形式,在未增加計算量的同時能夠獲得較大的穩定區域和較高的計算精度。

對流擴散方程;譜元法;穩定性;半隱式Adams方法

對流擴散方程是描述流體流動和傳熱、污染物輸移和擴散、電化學反應等的典型方程之一,利用數值方法進行求解時,由于對流項的存在,求解過程可能會出現不穩定現象,因此數值方法的穩定性問題一直是對流擴散方程研究的熱點。當對流擴散方程的對流項占優時,應用傳統的有限差分法和有限元法求解會出現數值振蕩[1-2],Gottlieb等在利用擬譜方法求解時也發現了不穩定現象[3],而Mofid等通過引入罰方法來處理邊界條件能夠部分或完全避免這種不穩定現象[4]。

譜元方法[5]結合了譜方法的高精度和有限元法的靈活性特點,使得對流擴散問題求解有望獲得高精度的數值解。目前,譜元方法應用的主要障礙是高雷諾數Re下的穩定性問題。因為譜元方法在單元上需對求解變量進行譜近似,當Re增大、黏性耗散作用減小時,任意微小擾動都會引起單元數值解不穩定且最終擴展到整個求解區域。為了擴大Re范圍,一些穩定性措施[6-7]引入到了譜元方法之中。

本文在前期譜元方法[8]研究的基礎上,采用特征分析法系統地分析了Chebyshev譜元方法的半離散形式和Chebyshev譜元方法耦合半隱式Adams時間離散方法的全離散形式的穩定性條件,討論了半隱式Adams時間離散方法中對流項和黏性項在不同插值階數、網格劃分、時間步長時對穩定性的影響,探索了最優離散格式,試圖擴大穩定區域,提高計算精度和計算效率,最后結合具體算例對Chebyshev譜元方法耦合半隱式Adams方法在求解對流擴散方程時的有效性進行了驗證。

1 對流擴散方程

一維對流擴散方程為

(1)

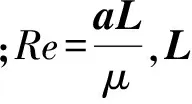
u(x,0)=u0(x)

(2)

u(0,t)=g1(t);u(1,t)=g2(t)

(3)

2 譜元方法

僅考慮Re影響,式(1)的Galerkin變分形式為

(4)

原微分方程的變分問題:求u∈H1使得

B(u,v)=f(v), ?v∈H1

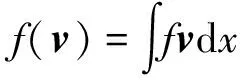
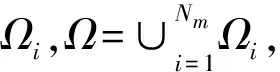
(5)

(6)

插值函數為

(7)

式中:Tm、Tn為Chebyshev多項式;Nx為單元網格數;cm滿足

(8)

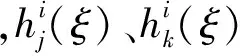
在標準單元內對式(4)進行離散得

(9)

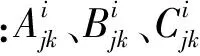
(10)

式(10)為u關于時間的一階線性常微分方程組。

3 時間離散

式(10)在時間上的逐步積分途徑一般有顯式和隱式兩種。顯式積分計算效率較高,需要的計算機內存相對較小,但計算精度較低,條件穩定;隱式積分的精度高,穩定性較好,但每一個積分步都要求解一個線性方程組,不便于直接計算。本文時間項采用半隱式Adams方法進行離散,對流項采用Je階顯式Adams-Bashforth形式,黏性項采用Ji階隱式Adams-Monlton形式[9],這樣便融合了顯式方法耦合簡單和隱式方法穩定性好的特點。式(10)的全離散形式為

(11)

式中:βj為Adams-Bashforth系數[10];γk為Adams-Monlton系數[10]。

4 譜元方法的穩定性分析

4.1 半離散方程的穩定性

將式(10)兩側左乘B的逆矩陣可得

(12)

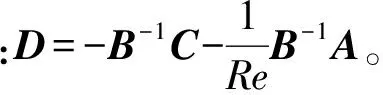
由于僅考慮第一類邊界條件,所以在邊值計算中不引入誤差,而假定在初值的計算中引入了擾動ε0,擾動ε滿足

(13)

式中:ε=(ε1,ε2,…,εn-1);L為D的內配置點n-1階子矩陣。

根據Lyapunov穩定性理論[11],式(12)穩定的充要條件為矩陣L的一切特征根都有非正實部,且每個有0實部的特征根對應矩陣L的約當標準形中的一維約當塊。也就是說,如果存在一個有正實部的特征根,式(12)對于任何時間離散都是不穩定的。矩陣L的特征值實部最大值與Re、單元數、單元網格數的關系如圖1所示。

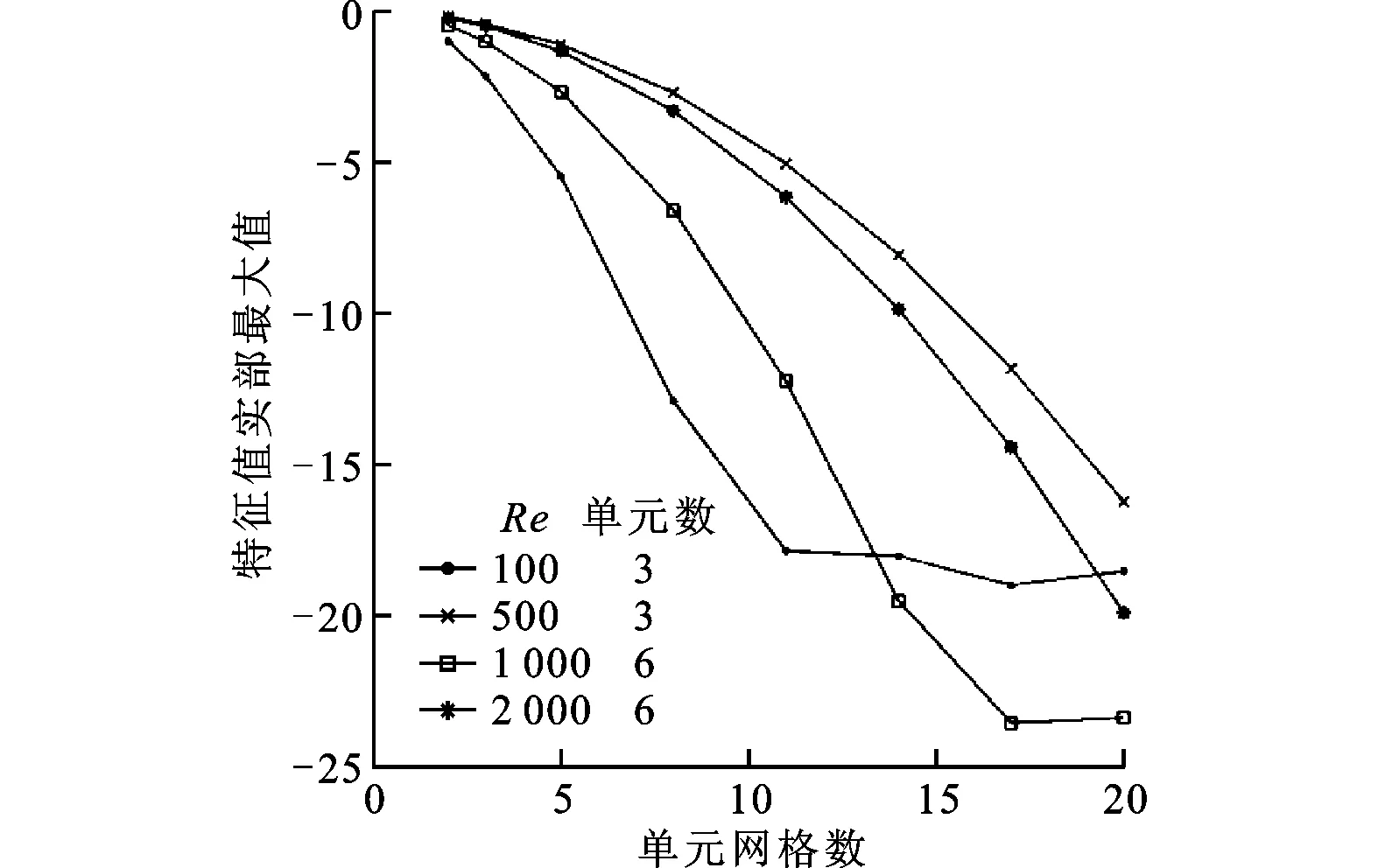
圖1 特征值實部最大值與單元數、單元網格數的關系

對于不同的Re和單元網格數,圖1中2種單元劃分的空間譜元離散始終滿足半離散方程穩定性要求,其他單元劃分的情形也可以進行驗證。

4.2 全離散方程的穩定性

4.2.1 單步法全離散的穩定性條件 采用半隱式Adams法時間離散,對流項、黏性項的插值階數均為1,即n+1時刻的變量僅與n時刻的變量相關時,式(11)可表示為

un+1=φ(ΔtC)un+φf(ΔtB)fn+1

(14)

式中:φ、φf為時間離散函數。

擾動ε的全離散形式為

εn+1=Lεn

(15)

Sousa分析了形如式(14)的全離散格式的穩定性條件[12],即:當L為正規矩陣時,其譜半徑ρ(L)≤1為穩定的充分條件;當L為非正規矩陣時,其譜半徑ρ(L)≤1僅為穩定的必要條件。可以驗證,當采用的Chebyshev函數為單元基函數時,L為正規矩陣,所以單步譜元法穩定的充分條件為ρ(L)≤1。

4.2.2 多步法全離散的穩定性條件 采用半隱式Adams法時間離散,對流項或黏性項的插值階數大于1,即n+1時刻的變量與前n-k+1時刻的變量相關時,式(11)可表示為

φj(ΔtDn-k+j)un-k+j+φf(ΔtB)fn+1

n=k,k+1,k+2,…

(16)

式中:φj、φf為時間離散函數;Dn-k+j為un-k+j的系數矩陣。

擾動ε的全離散形式為

n=k,k+1,k+2,…

(17)

式中:Lj為φj(ΔtDn-k+j)的內配置點n-1階子矩陣。

Dorsselaer等分析了形如式(16)的全離散格式的穩定性條件[13],定義擾動

Vn+1=((εn+1)T,(εn)T,…,(εn-k+1)T)T

滿足

Vn+1=EVn,n≥k

(18)

式中:I為單位矩陣;0為零矩陣。

多步譜元法穩定的充分條件為ρ(E)≤1。

4.3 不同形式全離散方程的穩定區域

通過選用4種不同的網格劃分方式,分別表示為3×5(Nm=3,Nx=5)、5×7(Nm=5,Nx=7)、10×6(Nm=10,Nx=6)、10×10(Nm=10,Nx=10),時間(計算時間與特征時間的比值)步長Δt∈[0.001,0.1],來比較不同網格劃分、時間步長和時間離散方式的求解穩定性。

對于半隱式Adams法時間離散,當對流項采用一階插值形式,黏性項分別采用一階、二階插值形式時,式(10)的全離散形式可分別表示為

(19)

(20)

將式(19)、式(20)分別表示為式(14)、式(16)的形式,即可由單步法和多步法的穩定性條件對求解穩定性進行判定。對流項一階插值,黏性項一階、二階插值時的求解穩定域如圖2所示。從圖2可以看出,黏性項二階插值的穩定域和一階插值基本相同,網格劃分對穩定域的影響很小,上臨界Re隨著時間步長的減小而逐步增大。

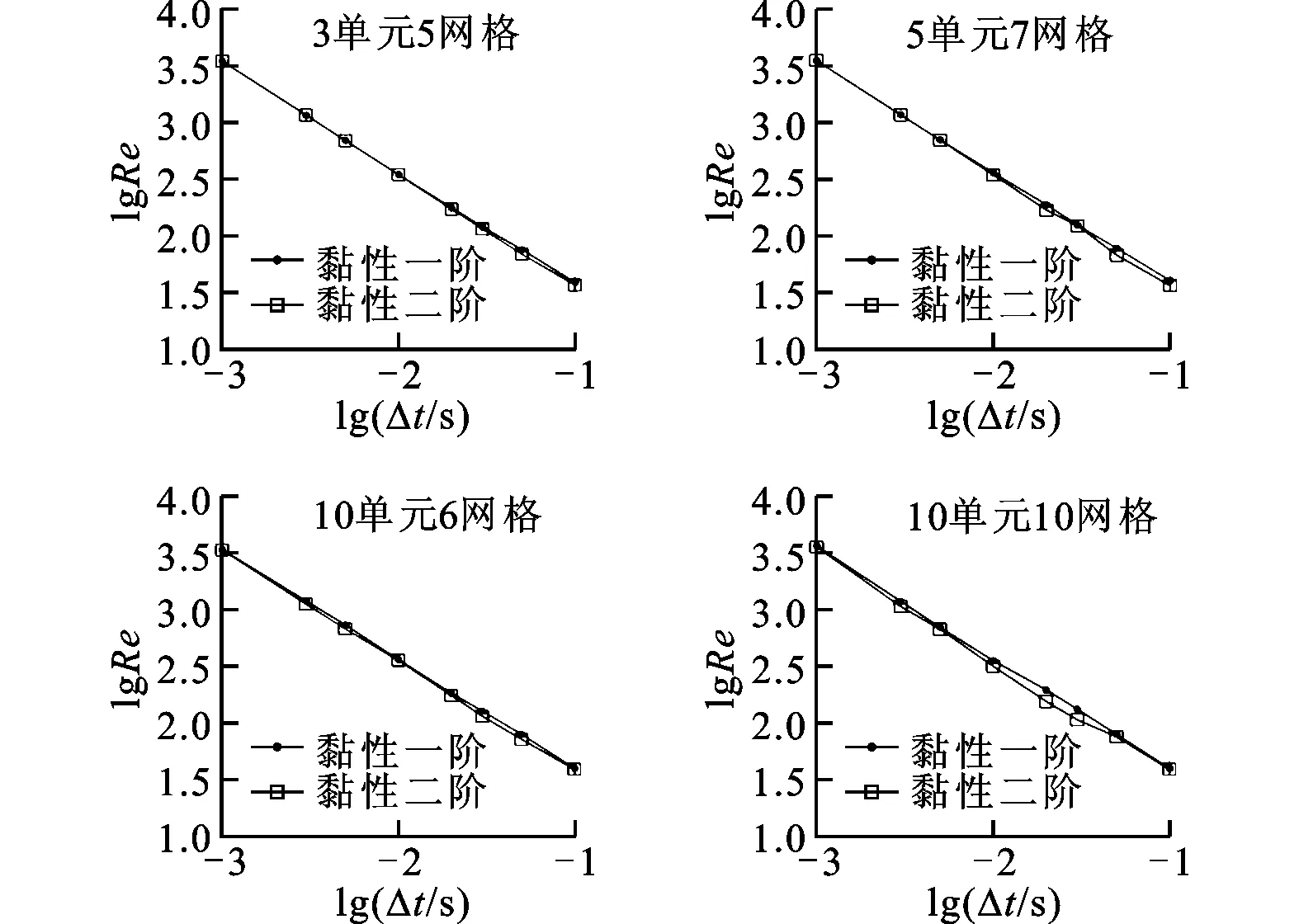
圖2 黏性項不同插值階數的穩定性曲線

對于半隱式Adams法時間離散,對流項采用一階插值形式,黏性項采用三階插值形式時,式(10)的全離散形式可表示為

(21)

將式(21)表示為式(16)的形式,利用多步法穩定性條件對求解穩定性進行判定。對流項一階插值、黏性項三階插值時的求解穩定域如圖3所示。從圖3可以看出,黏性項三階插值時,不僅存在上臨界Re,也存在下臨界Re,只有當Re位于上臨界Re和下臨界Re之間時求解才是穩定的。上臨界Re隨時間步長的增大而減小,下臨界Re隨時間步長的增大而增大,同時求解穩定域隨網格節點數的增加而減小。黏性項三階插值對求解的穩定性的影響很大,且顯著減小了穩定域的范圍。

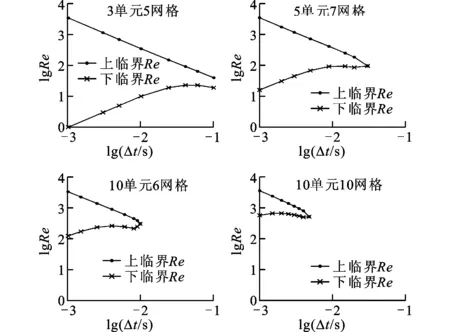
圖3 黏性項三階插值的穩定性曲線

對于半隱式Adams法時間離散,當黏性項采用一階插值形式,對流項分別采用二階、三階插值形式時,式(10)的全離散形式可表示為

(22)

(23)

將式(22)、式(23)表示為式(16)的形式,同樣利用多步法穩定性條件對求解穩定性進行判定。黏性項一階插值,對流項一階、二階、三階插值時的求解穩定域如圖4所示。從圖4可以看出:對流項二階插值存在臨界時間步長,上臨界Re在時間步長大于臨界值時有所減小,在時間步長小于臨界值時大幅度增加;對流項三階插值也存在臨界時間步長,上臨界Re在時間步長大于臨界值時比二階插值進一步減小,在時間步長小于臨界值時迅速增加到無窮大。網格節點數對臨界時間步長的影響也很大,隨節點數的增加,臨界時間步長減小,對于10×10的網格劃分,二階、三階插值的臨界時間步長均小于0.001。

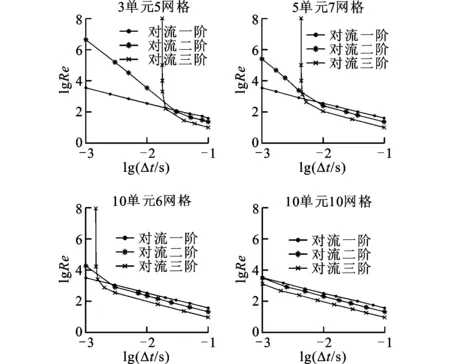
圖4 對流項不同插值階數的穩定性曲線

5 計算實例和數值結果

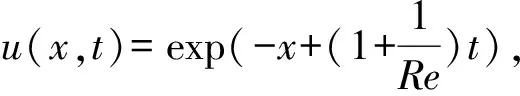
(24)

統一選取時間步長Δt=0.001,比較3單元5網格和10單元10網格2種網格劃分,并給出t=1.0時的計算誤差。

5.1 單步法全離散數值結果

單步法全離散的數值結果如圖5所示。Re小于上臨界Re時,2種網格劃分都取得了正確的數值結果,但由于時間離散階數較低,所以數值結果的精度不高。Re大于上臨界Re時,10單元10網格的數值結果快速發散,3單元5網格的數值結果雖有發散的趨勢,但速度非常平緩,說明節點數越多,不穩定作用越強。

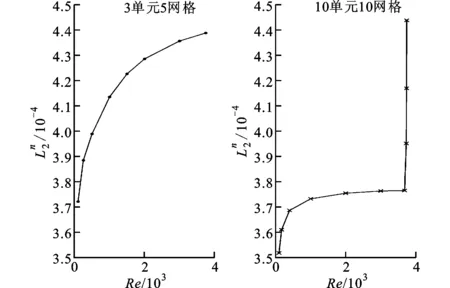
圖5 單步譜元法的計算誤差

5.2 多步法全離散數值結果

對流項采用一階插值,黏性項采用二階、三階插值時的數值結果如圖6所示。對于黏性項二階插值,當Re小于上臨界Re時,計算誤差和一階插值相差很小;當Re大于上臨界Re且節點數較多時,數值結果的發散速率遠大于節點數較少時的發散速率。黏性項三階插值的計算誤差和二階插值基本相同,當Re大于上臨界Re或小于下臨界Re且節點數較多時,數值結果快速發散。

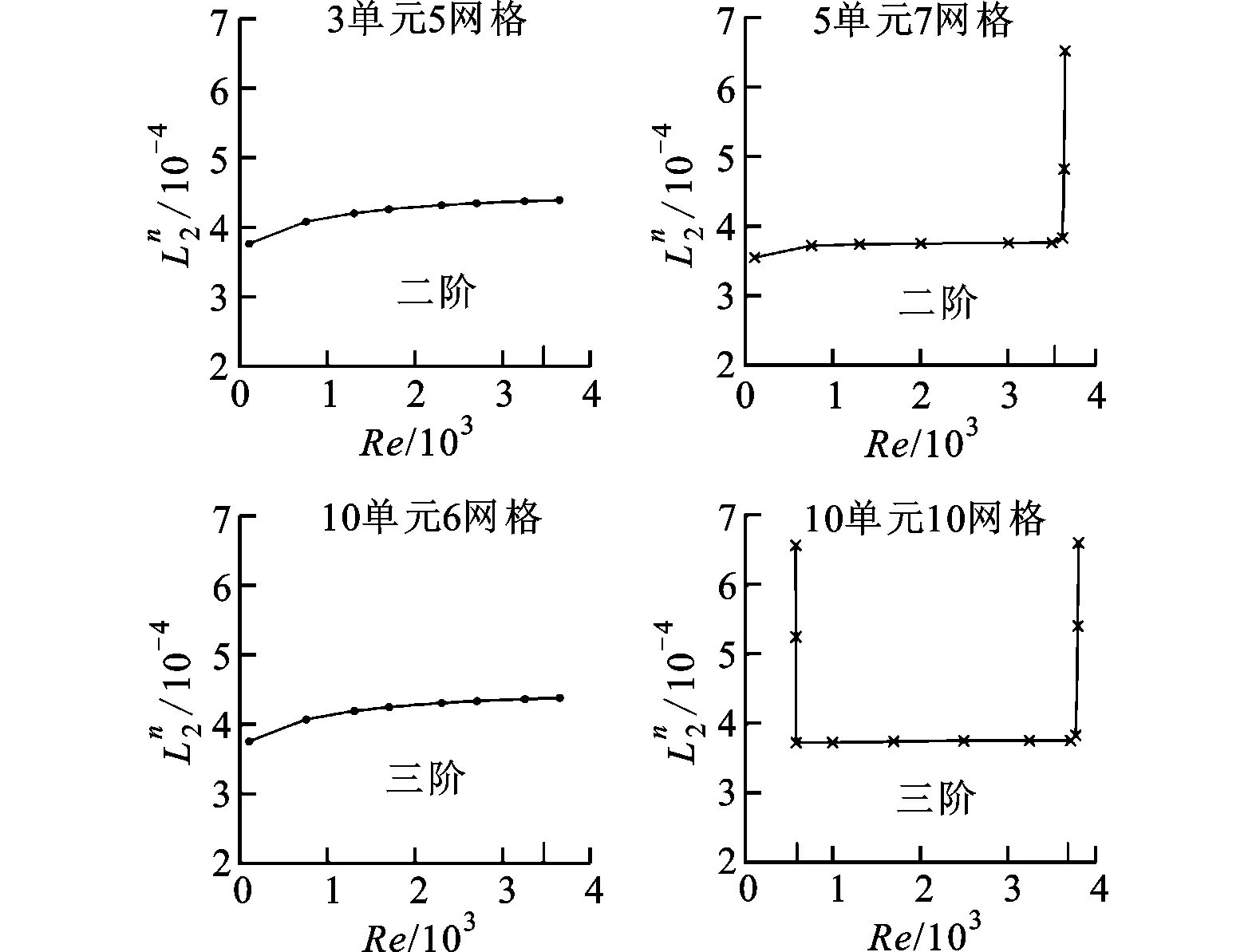
圖6 黏性項二階、三階插值的計算誤差

黏性項采用一階插值,對流項采用二階、三階插值時的數值結果如圖7所示。對流項采用二階插值時,計算誤差相較一階插值大大減小,同時Re較大時的誤差下降更多,Re大于上臨界Re且節點數較多時,數值結果快速發散。對流項三階插值的計算精度與二階插值基本相同。

圖7 對流項二階、三階插值的計算誤差

6 結 論

本文采用Chebyshev譜元方法耦合半隱式Adams時間離散方法求解了一維對流擴散方程,并對求解過程中方程的半離散和全離散形式的穩定性條件進行了討論,分析了半隱式Adams時間離散對流項、黏性項在不同插值階數、網格劃分和時間步長時對求解穩定性及計算精度的影響,得出如下結論。

(1)對流擴散方程的空間譜元離散,對于任意的Re,網格劃分都滿足半離散方程的穩定性條件。

(2)隨著對流項插值階數的增加,求解穩定域得到了擴大,計算精度大大提高。對流項二階插值、時間步長小于臨界值時,上臨界Re能取得較大的值;時間步長大于臨界值時,上臨界Re減小幅度減緩,適宜在實際數值計算中應用。

(3)隨著黏性項插值階數的增加,求解穩定域縮小。三階插值時出現了下臨界Re,穩定域大大減小。

今后的工作可以從以下兩方面展開:在方程中通過增加譜消除人工黏性項,使得譜元方法能夠求解的穩定區域擴大;探索高精度的時間處理方法,如時空耦合的最小二乘譜元方法。

[1] GE L X, ZHANG J. High accuracy iterative solution of convection diffusion equation with boundary layers on nonuniform grids [J]. Journal of Computational Physics, 2001, 171(2): 560-578.

[2] ZIENKIEWICZ O C, HEINRICH J C. The finite element method and convection problems in fluid mechanics [M]. New York, USA: John Wiley & Sons Inc., 1978: 1-22.

[3] GOTTLIEB D, ORSZAG S A. Numerical analysis of spectral method: theory and application [M]. Philadelphia, PA, USA: SIAM, 1977: 139-143.

[4] MOFID A, PEYRET R. Stability of the Chebyshev collocation approximation to the advection-diffusion equation [J]. Computers Fluids, 1993, 22(4/5): 453-465.

[5] PETERA A T. A spectral element method for fluid dynamics: laminar flow in a channel expansion [J]. Journal of Computational Physics, 1984, 54(3): 468-488.

[6] FISCHER P, MULLEN J. Filter-based stabilization of spectral element methods [J]. Comptes Rendus de L’Académie des Sciences, 2001, 332(3): 265-270.

[7] XU C J, PSAQUETTI R. Stabilized spectral element computations of high Reynolds number incompressible flows [J]. Journal of Computational Physics, 2004, 196(2): 680-704.

[8] 秦國良, 徐忠. 譜元方法求解二維不可壓縮Navier-Stokes方程 [J]. 應用力學學報, 2000, 17(4): 20-26. QIN Guoliang, XU Zhong. A spectral element method for incompressible Navier-Stokes equations [J]. Chinese Journal of Applied Mechanics, 2000, 17(4): 20-26.

[9] 陳雪江, 秦國良, 徐忠. 譜元法和高階時間分裂法求解方腔頂蓋驅動流 [J]. 計算力學學報, 2002, 19(3): 281-285. CHEN Xuejiang, QIN Guoliang, XU Zhong. Spectral element method and high order splitting method for Navies-Stokes equation [J]. Chinese Journal of Computational Mechanics, 2002, 19(3): 281-285.

[10]WILLIAM GEAR C. Numerical initial value problem in ordinary differential equations [M]. Englewood Cliffs, NJ, USA: Prentice-Hall Inc., 1973: 147-158.

[11]張家忠. 非線性動力系統的運動穩定性、分岔理論及其應用 [M]. 西安: 西安交通大學出版社, 2010: 12-19.

[12]ERCILIA S. The controversial stability analysis [J]. Applied Mathematics and Computation, 2003, 145(2/3): 777-794.

[13]VAN DORSSELAER J L M, HUNDSDORFER W. Stability estimates based on numerical ranges with an application to a spectral method [J]. BIT Numerical Mathematics, 1994, 34(2): 228-238.

[本刊相關文獻鏈接]

耿艷輝,秦國良.Chebyshev譜元法求解含吸收邊界的二維均勻穩定流場的聲傳播.2012,46(3):100-106.[doi:10.7652/xjtuxb201203018]

詹飛龍,張楚華.對流擴散方程的擬譜格式穩定性分析及擴穩方法.2012,46(3):113-118.[doi:10.7652/xjtux2012030 20]

孫旭,張家忠,黃科峰.基于彈簧近似的非結構化網格自適應處理方法.2010,44(9):104-108.[doi:10.7652/xjtuxb2010 09021]

章爭榮,張湘偉.對流擴散方程的數值流形格式及其穩定性分析.2010,44(9):104-108.[doi:10.7652/xjtuxb201009021]

張榮欣,秦國良.用切比雪夫譜元方法求解均勻流場中的聲傳播問題.2009,43(7):120-124.[doi:10.7652/xjtuxb2009 07026]

朱昌允,秦國良,徐忠.譜元方法求解波動方程時顯式與隱式差分方法的比較.2008,42(9):1142-1145.[doi:10.7652/xjtuxb200809017]

朱昌允,秦國良,徐忠.譜元方法求解波動方程及影響其數值精度的相關因素.2008,42(1):56-59.[doi:10.7652/xjtuxb 200801013]

許靖,秦國良,朱昌允.譜元方法求解含吸收邊界的聲學問題.2007,41(7):875-878.[doi:10.7652/xjtuxb200707027]

(編輯 苗凌)

Spectral Element Method for Convection-Diffusion Equation with Stability Analysis

HE Wenqiang,QIN Guoliang

(Institute of Fluid Machinery, Xi’an Jiaotong University, Xi’an 710049, China)

The Chebyshev spectral element method combining with the semi-implicit Adams method is presented for solving the one-dimensional convection-diffusion equation, and the feasibility is verified by a numerical example. The stability condition of different discrete forms of spectral element method is deduced with character analysis, and the influences of time step, grid partitioning, interpolation order of convective and viscous terms are discussed. It is demonstrated that numerical solution with high accuracy can be gained with the coupled spectral element and semi-implicit Adams method for the convection-diffusion equation. Larger stability domain and higher accuracy can be achieved without extra-calculation as first-order viscous terms and second-order convective terms are interpolated in Adams method.

convection-diffusion equation; spectral element method; stability; semi-implicit Adams method

2014-04-21。

和文強(1982—),男,博士生;秦國良(通信作者),男,教授,博士生導師。

國家重點基礎研究發展規劃資助項目(2012CB026004)。

時間:2014-10-31

10.7652/xjtuxb201501001

O357.1

A

0253-987X(2015)01-0006-01

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1643.019.html