強度折減法與極限平衡法對比分析——以安康市一邊坡為例
袁茂蓮 趙天彪 巫正海 林 遠
(1.西南石油大學地球科學與技術學院,四川 成都 610500;2.四川建筑職業技術學院交通與市政工程系,四川 德陽 618000;3.西南石油大學土木工程與建筑學院,四川 成都 610500)
0 引言
邊坡穩定性分析是邊坡設計的前提。然而這個問題至今仍未得到妥善解決,因為解決這一問題必須先要查清坡體的地質狀況及其強度參數,同時又要有科學合理的分析方法[1]。對于均質土坡,可以通過各種優化方法來搜索危險滑動面;但是對于巖質邊坡,由于實際巖體中含有大量不同構造、產狀和特性的不連續結構面,傳統極限平衡方法尚不能搜索出危險滑動面以及相應的穩定安全系數。而有限元強度折減法是通過不斷降低邊坡巖土體的抗剪切強度參數,使其達到極限破壞狀態為止,從而得到邊坡的強度儲備安全系數,使邊坡穩定分析進人了一個新的時代[2-4]。
1 有限元強度折減安全系數定義
邊坡穩定性分析中,安全系數是評價邊坡穩定性的一個重要指標。對于邊坡安全系數的定義,在巖土工程歷史中共經歷了三次大的變化:第一次是采用的力矩定義[5],第二次采用的是剪應力定義[6],第三次采用的是抗剪強度折減定義[7-8]。其中,前兩次定義都是基于極限平衡理論,而第三次關于抗剪強度折減的定義,其實質與用剪應力定義是一致的。但是,它為土坡穩定性分析的數值實施提供了理論依據,使得通過數值計算得到邊坡的整體安全系數成為現實。
對于摩爾—庫侖材料,抗剪強度折減安全系數可表示為:
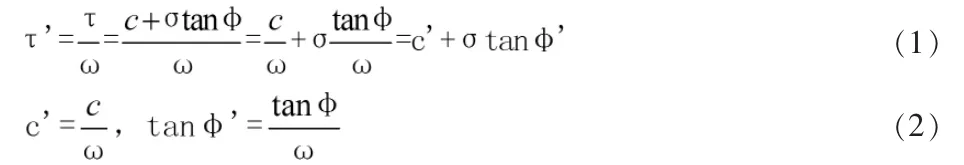
此強度折減形式的安全系數定義與邊坡穩定分析的極限平衡條分法安全系數的定義形式是一致的。
2 強度折減理論中邊坡失穩判據
有限元強度折減法分析邊坡穩定性的一個關鍵問題是如何根據有限元計算結果來判別邊坡是否處于破壞狀態。目前的失穩判據主要有兩類:
(1)在有限元計算過程中采用力和位移的不收斂作為邊坡失穩的標志。
(2)以廣義塑性應變或者等效塑性應變從坡腳到坡頂貫通作為邊坡破壞的標志。
塑性區貫通并不一定意味著破壞,塑性區貫通是破壞的必要條件,但不是充分條件,還要看是否產生很大的且無限發展的塑性變形和位移,有限元計算中表現為塑性應變和位移產生突變[9]。
土體整體破壞的標志應是滑體出現無限移動,此時滑移面上的應變會出現突變。同時,有限元計算也會出現計算不收斂。由此可見,上述(1)(2)兩種判據是一致的[10]。
3 屈服準則的選用
有限元強度折減法中巖土材料本構模型采用理想彈塑性模型,安全系數大小與采用的屈服準則密切相關,不同的準則會得出不同的安全系數。
本文采用ABAQUS6.10 對邊坡穩定性進行數值計算,在ABAQUS軟件中采用D-P 準則。該準則是在米賽斯準則的基礎上,考慮平均壓應力而將米賽斯條件推廣成為如下公式:


式中,I1和J2分別為應力張量的第一不變量和應力偏張量的第二不變量,α 及k 是與巖土材料內摩擦角φ 和粘聚力c 有關的系數。
4 實例應用
湖景嘉苑小區位于安康市漢濱區瀛湖鎮郭家店境內。以西為瀛湖鎮街道;以東為永久性擋土墻和原修建安康水電站專用鐵路線及民房;北為居民區;南為該小區正建2# 樓場地。整個場地東高西低。
4.1 巖性參數
根據勘探揭露,場地土層在勘探深度內巖土層主要為:粉質粘土和千枚巖,對應建立模型設置上層為彈塑性介質(土體),c 取24kPa,φ 取17°,γ 取19.6,泊松比0.3;下層為彈性介質(強風化千枚巖),c取10KPa,φ 取35°,γ 取23,泊松比0.25,彈性模量1.2 GPa。
4.2 穩定性系數計算
4.2.1 有限元強度折減法計算結果
本文以該邊坡的工程地質勘察剖面為原型建立數值模型,采用ABAQUS6.10 數值模擬軟件進行模擬。在數值模擬中,兩層土體均采用理想線彈性模型,選取場變量FV1 自0.5-2.0,每間隔0.25 進行一次強度折減。建立的有限元網格模型以一個剖面為例,如圖1。
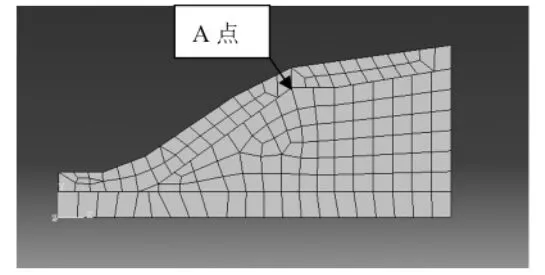
圖1 邊坡有限元網格模型
本文選擇點A 作為場變量(FV1)和X 方向位移(U1)關系曲線的結點,利用ABAQUS 提供的Combine 函數,將FV1 隨U1 的變化關系繪制出來,見圖2。從圖2 中可以看出,A 結點水平位移有一個明顯的拐點,本文以拐點作為邊坡不穩定的評價標準,則安全系數Fs=1.31。

圖2 場變量與X 方向位移關系曲線

圖3 位移等值線云圖
從圖4 中,t=0.5689s 的PEMAG 圖中清楚的表明了邊坡失穩過程。即從一開始是A 點附近的表層土體出現屈服,并向下滑動,隨后下側土體擠壓坡腳土體,導致坡腳土體發生塑性變形。

圖4 積分點上的等效塑性應變
采用上述方法計算出其他剖面穩定性安全系數如表1:
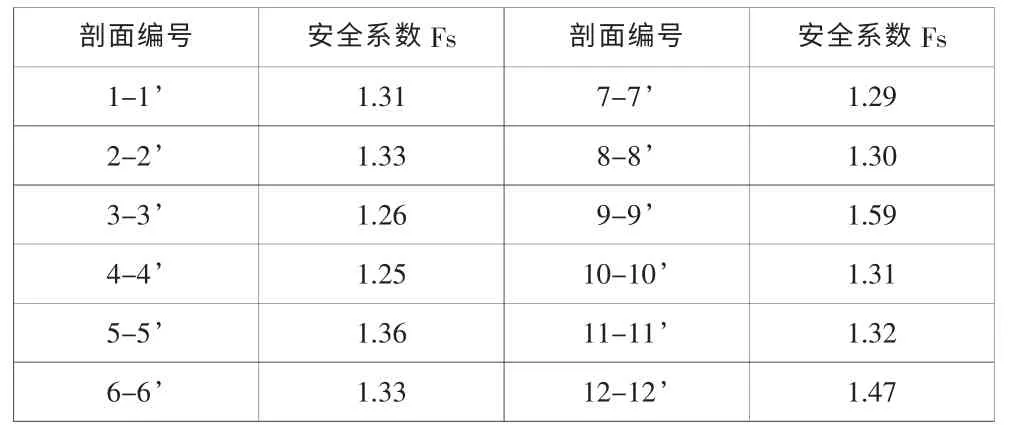
表1 數值模擬穩定性計算結果
由數值計算結果可以看出:在天然狀態下,勘察區內斜坡穩定系數Fs=1.25~1.59,說明在天然狀態下斜坡處于穩定狀態。
4.2.2 極限平衡法計算結果
勘察區斜坡荷載類型包括斜坡巖體自重靜載荷和道路動載荷。本文主要目的是將有限元強度折減法與極限平衡法做對比,所以此處荷載工況僅考慮天然自重工況。
該區斜坡土質覆蓋層較厚,根據《建筑邊坡工程技術規范》(GB50330-2002)規范,采用復雜土層折線性計算公式對斜坡進行驗算。根據《滑坡防治工程勘查規范》(DZ/T0218-2006),安全穩定性系數fst 取1.15,計算結果見表2。
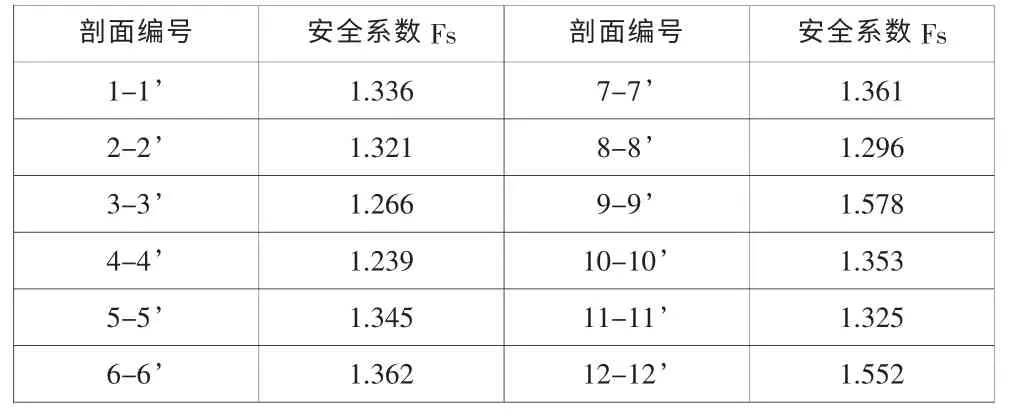
表2 斜坡穩定性計算結果
由計算結果可以看出:在天然狀態下,勘察區內斜坡穩定系數Fs=1.239~1.578,說明在天然狀態下斜坡處于穩定狀態。
4.3 對比分析
通過對比以上兩種計算結果,可以發現,強度折減法與極限平衡法相比總體都偏于不保守,其相對誤差為0.31-5.28%,在工程允許范圍內,也說明有限元強度折減法在求解邊坡穩定性系數上是可行的。
5 結論
通過本文以一邊坡工程實例,將有限元強度折減法與傳統的極限平衡法計算邊坡穩定性系數并進行比較,可以得出如下結論:
(1)有限元強度折減法計算的邊坡穩定性系數與傳統極限平衡法計算結果較為接近,可以作為工程參考;
(2)極限平衡法計算結果較有限元強度折減法更為保守;
(3)數值模擬邊坡變形破壞結果更為形象直觀,但也存在滑動面不清晰的缺陷。
[1]陳祖煜.土質邊坡穩定分析:原理、方法、程序[M].北京:水利水電出版社,2003.
[2]Griffiths D V,Lane P A.Slope stability analysis by finite elements[J].Geotechnique,1999,49(3):387-403.
[3]Dawson E M,Roth W H,Drescher A.Slope stability analysis by strength reduction[J].Geotechnique,1999,49(6):835-840.
[4]宋二祥,高翔,邱玥.基坑土釘支護安全系數的強度參數折減有限元法[J].巖土工程學報,2005,27(3):258-263.
[5]Fellinius W.Calculation of stability of earth dams[C]//Trans 2ndinternational congress of large dams,1936(4):445.
[6]Bishop A W.The use of the slip circle in the stability analysis of slopes[J].Geotechnique,1955(5):7-17.
[7]Duncan J M.State of the art:limit equilibrium and finite element analysis of Slope[J].Journal of Geotechnical Engineering,ASCE,1996,122(7):577-595.
[8]Zienkiewicz O C,Humpheson C and Lewis R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique,1975,25(4):671-689.
[9]鄭穎人,趙尚毅.有限元強度折減法在土坡與巖坡中的應用[J].巖石力學與工程學報,2004,23(19):3381-3388.
[10]鄭穎人,趙尚毅,宋雅坤.有限元強度折減法研究進展[J].后勤工程學院學報,2005,3:1-6.

