要返回操作中感悟
——小學數學教學中動手操作注意的問題

劉斌

要返回操作中感悟
——小學數學教學中動手操作注意的問題

劉斌

在小學數學教學中，學生操作感知后再立足模型的本質特征返回操作中思考感悟，可以及時利用操作經驗和成果升華思維，建構模型，這樣才能有效實現操作和思維的融合，充分發揮操作在促進小學生思維發展方面的巨大作用。

一、針對本質特征，返回操作中感悟概念

我們先看兩位教師教學分數的再認識（新人教版五年級下冊），分別拿出1、4、8、12個圓片的并圖示說明：

A教師：以前我們都是把一個物體看成一個整體，通過剛才的操作，你對整體有什么新認識？

生1：不僅一個物體可以看成一個整體，多個物體也可以看成一個整體。

生2：多組物體也可以看成一個整體。

師：真完整。不僅一個物體可以看成一個整體，多個、多組物體都可以看成一個整體。

（教師邊小結邊把1、4、8、12個圓片圈起來并板書——整體：一個、多個、多組）

師：現在的分數跟以前學的分數有什么相同點和不同點？

（師生共同總結出分數的意義。）

（B教師小結標明整體的意思后并沒有馬上總結分數的意義，而是引導學生返回操作中思考感悟。）

師：老師又有疑問了——每次拿出的圓片數不一樣呀，為什么都是呢？

生：因為都是把一個整體平均分成4份，取出其中的3份。

師：前后連起來說就是——不管整體是多還是少，只要把一個整體平均分成4份，表示其中的3份都是嗎？

（全體學生點頭稱是。）

A教師的做法比較普遍。因為教學進行到這兒學生頭腦中已被賦予了整體新的含義，自然會在新整體的環境下完善分數的意義。殊不知此時學生只是根據分數的初步認識再聯系除法、乘法的意義拿出相應的圓片而己，遠沒有上升到新高度來順應分數的意義。B教師先以“不都是拿出圓片的嗎，為什么拿出的圓片數不一樣”的問題引導學生返回操作中觀察思考，在圖示的指引下“學生爭相答道：因為總數不一樣，拿出的就不一樣。還有學生邊指圖邊一一解釋。整體的多種表象凸顯眼前，頭腦中確立了新整體的概念。又以“每次拿出的圓片數不一樣呀，為什么都是”這一問題引導學生再次返回操作中討說法，學生憑借圖示、操作經驗異中求同，找到共同特征：“不管整體是多還是少，只要把一個整體平均分成4份，表示其中的3份都是。”真正在新整體的環境下構建出分數的模型。兩次返回操作中的觀察思考淡化了操作過程的干擾，突出了概念本質的提煉，概念的構建分外明晰。

二、圍繞主要步驟，返回操作中說清算理

下面的教師在教學除法豎式（新人教版二年級下冊，下同）時就高明了許多：

師：今天要學習最難的豎式——除法的豎式（板題：除法的豎式）。先進行擺小棒寫算式比賽。13根小棒，每4根分一組，結果怎樣？

學生一邊擺一邊列算式。并思考交流：①列式理由。②算式含義。

師：怎樣的豎式能表明各個數的來歷呢？在紙上寫一寫。（課件出示探究要求：①寫出豎式。②標明豎式中每個數的來歷、含義）

教師巡視收集典型做法板演。

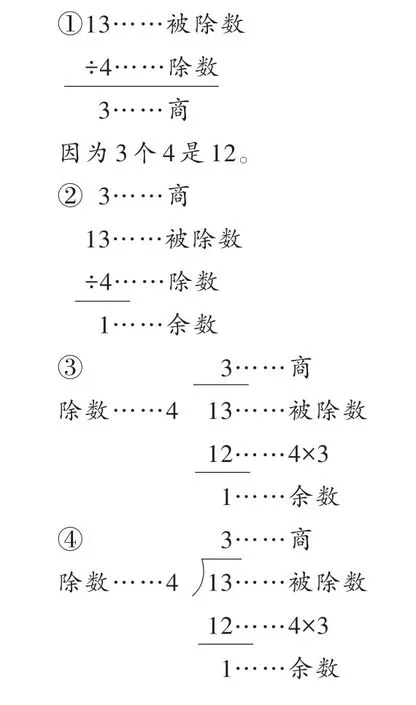
師：都有道理。能指出每種寫法的問題嗎？

學生陸續答道：第一種沒寫余數。第二種不知道余數是怎么來的。第三種除數、被除數要用線隔開。第四種沒寫含義。

師：每個數的含義是什么呢？

根據學生回答，教師寫出豎式④各個數的含義。課件同步閃示圖對應的部分。

教師邊指豎式④邊總結道：結合分小棒的過程，“13”除以“4”最多可以分3組，所以在個位商“3”，分完了3個4根也就是12根，所以在13的下面寫“12”,13根減12根等于1根，不夠分一組，也就是余數小于除數，說明商對了。確實等于3組余1根。

師：誰能簡潔地說出除法豎式的主要步驟？

（學生在豎式的相應位置板書：①商②乘③減④查。）

這位教師高明在不僅通過操作找到算法列出橫式，還讓學生在操作過程中思考交流橫式理由、橫式表示的含義，促進了操作、算式、實際含義的融合；不僅通過橫式發現豎式的寫法，還讓學生標明豎式中各數的來歷、含義，課件同步閃示圖對應的部分，主要算法數、形、意合一，交相輝映，學生知其然還知其所以然，全班學生當堂能用除法豎式正確熟練地求商。期末復習時平行班教師大呼很多學生又把除法豎式還給了老師，而我班就連每次考試不及格的敏敏都能正確用豎式求商。

三、立足必然聯系，返回操作中解釋原因

下面這位教師在教學“余數＜除數”時棋高一著：

小棒根數擺的結果算式

9根□□9÷4=2（個）…1（根）

10根

11根

12根

教師提問：想一想，13根、14根、15根、16根呢？

教師巡視指導。

全班交流，教師同步在課件上完成探究記錄表。

師：觀察記錄表，你能發現什么？小組內說說。

組1：除數都是4，余數有1、2、3。

組2：余數＜除數。

……

師：為什么余數只有1、2、3，沒有4、5、6……呢？

生3：因為夠4根就能拼成一個正方形。

師：1根不剩，所以余數是0。

生4：假設還剩5根，其中的4根拼成一個正方形，還是剩1根。

……

伴隨學生的回答，課件同步印證。

此片段的獨到之處是：學生觀察操作記錄表發現“余數＜除數”的規律后，教師并沒有繼續下文，而是順勢反問：“為什么余數只有1、2、3，沒有4、5、6……呢？”學生依據操作經驗義正辭嚴地一一推理作答，課件同步印證，規律的構建事實清楚，因果必然，當然牢不可破了。

從動手操作到符號表征，從形象思維到抽象思維還有一個感悟、貫通的過程。學生操作得出結論后還要抓住模型的主要特征及時引導學生返回操作中思考感悟，以促進二者的融合，實現無縫銜接，這樣才能充分發揮動手操作的功能，實現高效學習。

（作者單位：谷城縣粉陽路小學）

責任編輯 劉玉琴