分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)的全局漸近穩(wěn)定性

崔世維，蓋明久，劉孝磊

（海軍航空工程學(xué)院a.研究生管理大隊(duì)；b.基礎(chǔ)部，山東煙臺(tái)264001）

分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)的全局漸近穩(wěn)定性

崔世維a，蓋明久b，劉孝磊b

（海軍航空工程學(xué)院a.研究生管理大隊(duì)；b.基礎(chǔ)部，山東煙臺(tái)264001）

研究了分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)的全局漸近穩(wěn)定性，通過(guò)LMI方法得到了一種實(shí)現(xiàn)系統(tǒng)全局漸近穩(wěn)定性的LMI形式條件，通過(guò)實(shí)例仿真驗(yàn)證了結(jié)論的正確性。

分?jǐn)?shù)階；神經(jīng)網(wǎng)絡(luò)；漸近穩(wěn)定性；LMI

隨著對(duì)分?jǐn)?shù)階微積分的認(rèn)識(shí)越來(lái)越深刻，分?jǐn)?shù)階微積分在多個(gè)學(xué)科有廣泛應(yīng)用，如物理、化學(xué)、生物和圖像處理等，并且取得了較好的研究成果，凸顯了其獨(dú)特的優(yōu)勢(shì)和不可替代性，其理論和應(yīng)用研究引起了廣泛重視，已經(jīng)成為當(dāng)前國(guó)際上的一個(gè)研究熱點(diǎn)[1-7]。

眾所周知，小到一個(gè)具體的控制系統(tǒng)，大至社會(huì)系統(tǒng)、金融系統(tǒng)、生態(tài)系統(tǒng)，總是在各種偶然的或持續(xù)的干擾下進(jìn)行的，保持系統(tǒng)的穩(wěn)定性就顯得至關(guān)重要。因此，研究分?jǐn)?shù)階系統(tǒng)也必不可免地面臨著對(duì)穩(wěn)定性的研究。目前，關(guān)于分?jǐn)?shù)階系統(tǒng)穩(wěn)定性的研究結(jié)果主要涉及分?jǐn)?shù)階系統(tǒng)的有限時(shí)穩(wěn)定性、魯棒穩(wěn)定性、Mittag-Leffler穩(wěn)定性等[8-11]。然而，由于分?jǐn)?shù)階微積分定義的不統(tǒng)一以及定義本身的復(fù)雜性，導(dǎo)致對(duì)分?jǐn)?shù)階系統(tǒng)穩(wěn)定性的研究面臨著眾多困難。

另一方面，由于神經(jīng)網(wǎng)絡(luò)良好的非線性映射能力、自學(xué)習(xí)適應(yīng)能力和并行信息處理能力，為解決不確定非線性系統(tǒng)的建模和控制提供了新思路。隨著分?jǐn)?shù)階微積分的發(fā)展，人們將分?jǐn)?shù)階微積分引入到神經(jīng)網(wǎng)絡(luò)，建立了分?jǐn)?shù)階神經(jīng)網(wǎng)絡(luò)，并取得了一定的研究成果。文獻(xiàn)[12]基于整數(shù)階Hopfield神經(jīng)網(wǎng)絡(luò)模型提出了分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)模型，并引起了人們對(duì)分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性及特殊結(jié)構(gòu)的動(dòng)力行為等方面的廣泛關(guān)注[13-15]。

本文研究了分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)的全局漸近穩(wěn)定性，得到了一種LMI形式的充分條件，并通過(guò)實(shí)例仿真驗(yàn)證了結(jié)論的正確性。

1 預(yù)備工作

定義1：[1-2]如果 f(t)∈C1(0,+∞)，那么稱

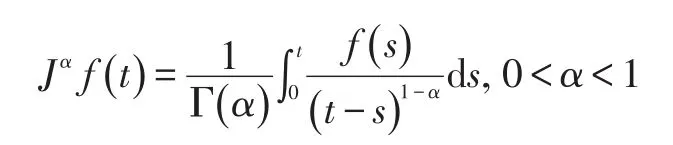
為函數(shù) f()

定義2：[1-2]如果 f(t)∈C1(0,+∞)，那么稱

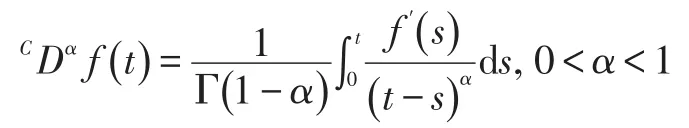
為函數(shù) f(t)的α階Caputo型分?jǐn)?shù)階導(dǎo)數(shù)。

為簡(jiǎn)便起見(jiàn)，下文將α階Caputo導(dǎo)數(shù)記為Dα。由文獻(xiàn)[1]知，Dα的Laplace變換式為

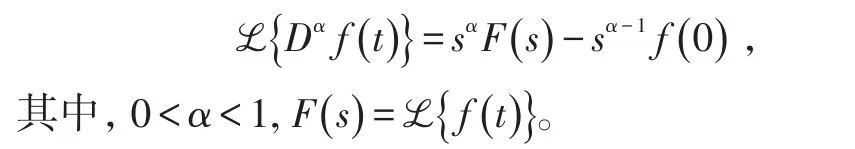
定義3：[1-2]Mittag-Leffler函數(shù)的單參數(shù)和雙參數(shù)分別定義為：

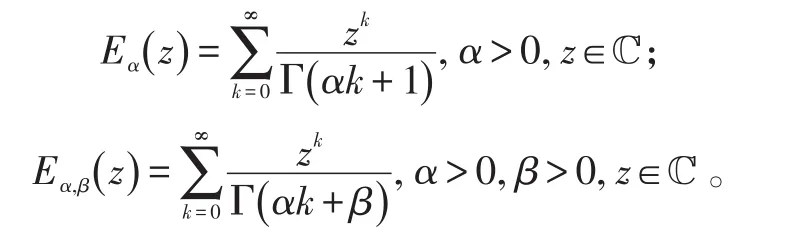
由文獻(xiàn)[1]知，雙參數(shù)Mittag-Leffler函數(shù)的Laplace變換式為：

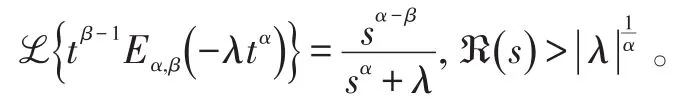
考慮如下分?jǐn)?shù)階神經(jīng)網(wǎng)絡(luò)：

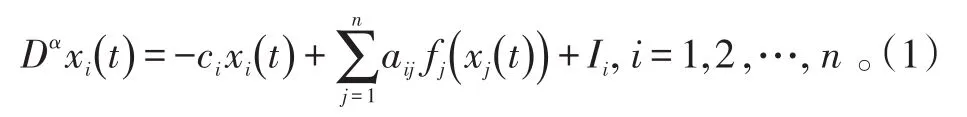
式（1）的向量形式為：

為研究分?jǐn)?shù)階系統(tǒng)的穩(wěn)定性，需要下面假設(shè)及引理。

假設(shè)1：激勵(lì)函數(shù) fi(·)(i=1,2,…,n)有界，且滿足Lipschitz條件，即存在Lipschitz常數(shù)li使得

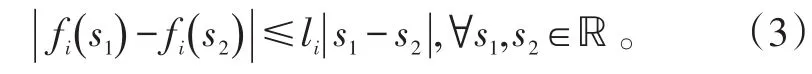
引理1：[1-2]Caputo導(dǎo)數(shù)Dα具有以下性質(zhì)：

1）Dαc=0，這里c為常數(shù)；

2）Dα(μf(t)+νg(t))=μDαf(t)+νDαg(t)，其中μ、ν為常數(shù)。

引理3：[16]假定x(t)∈為連續(xù)可微的向量函數(shù)，則對(duì)任意t≥t0，存在對(duì)稱正定方陣P使得下式成立：

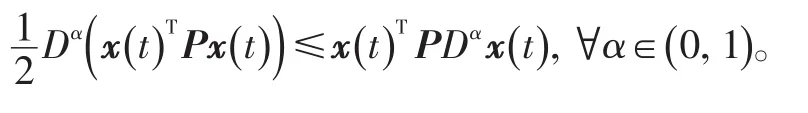
2 主要結(jié)果

定理1：若存在對(duì)稱正定方陣P，正對(duì)角矩陣Γ=diag[γ1,γ2,…,γn]＞0，使得下面LMI成立：

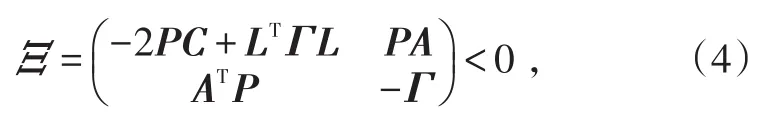
則系統(tǒng)是全局漸近穩(wěn)定的。

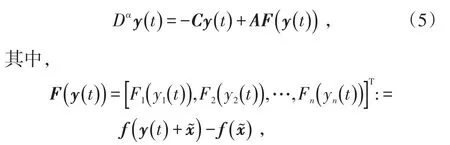
顯然F(0)=0。因此，為研究系統(tǒng)（1）的穩(wěn)定性，只需研究系統(tǒng)（5）零解的穩(wěn)定性。

下面構(gòu)造函數(shù)

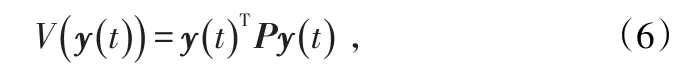
其中矩陣P滿足引理3，則

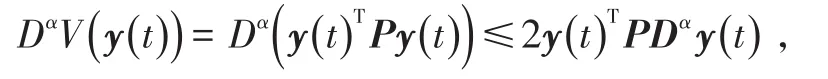
進(jìn)一步，

3 實(shí)例仿真

為系統(tǒng)（1）選取參數(shù)

通過(guò)Matlab軟件LMI工具包進(jìn)行求解，結(jié)果顯示LMI條件是可行的，可行解如下：

根據(jù)定理1可知系統(tǒng)是全局漸近穩(wěn)定的，圖1～3分別為x1(t)、x2(t)、x3(t)隨時(shí)間t(s)收斂于0的趨勢(shì)圖。

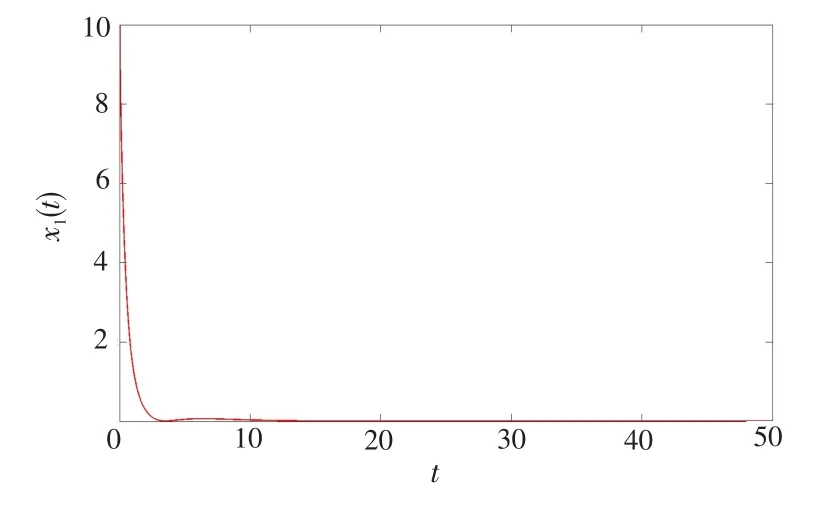
圖1 x1(t)隨時(shí)間t收斂于0的趨勢(shì)圖Fig.1 Tendency chart ofx1(t)converging to 0 witht

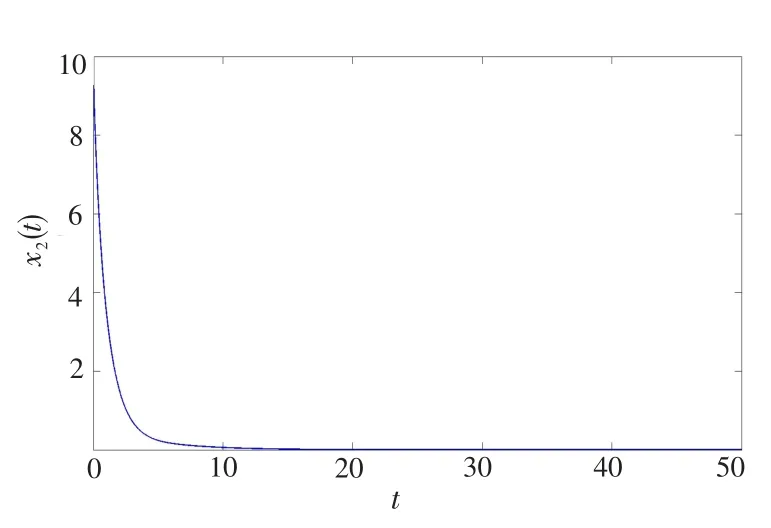
圖2 x2(t)隨時(shí)間t收斂于零的趨勢(shì)圖Fig.2 Tendency chart ofx2(t)converging to 0 witht

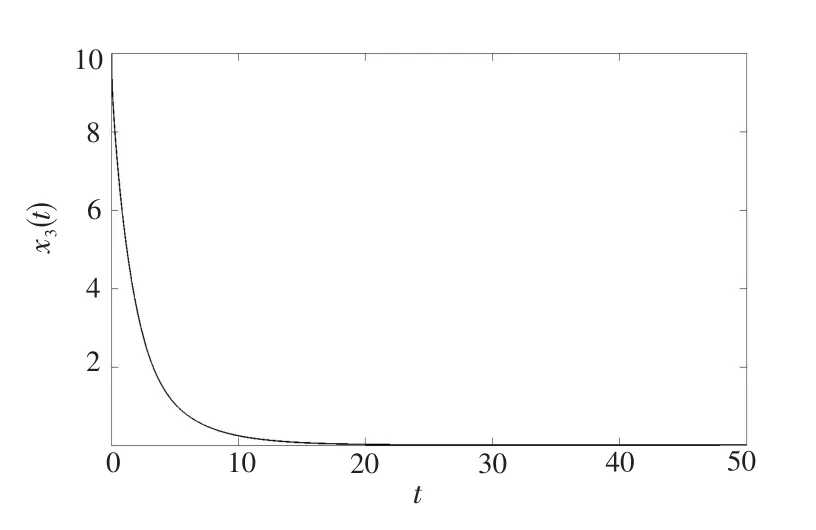
圖3 x3(t)隨時(shí)間t收斂于零的趨勢(shì)圖Fig.3 Tendency chart ofx3(t)converging to 0 witht

4 結(jié)論

本文通過(guò)對(duì)分?jǐn)?shù)階Hopfield型神經(jīng)網(wǎng)絡(luò)進(jìn)行全局漸近穩(wěn)定性分析，給出了判定該類系統(tǒng)全局漸近穩(wěn)定性的LMI條件，并進(jìn)行了Matlab仿真，通過(guò)實(shí)例驗(yàn)證了文中定理的正確性。

[1]PODLUBNY I.Fractional differential equations：an introduction to fractional derivatives，fractional differential equations，to methods of their solution and some of their application[M].New York：Academic Press，1998：78-81.

[2]KILBASAA，SRIVASTAVAH M，TRUJULLO J J.Theory and applications of fractional differential equations [M].Amsterdam：Elsevier Science Limited，2006：90-99.

[3]LAKSHMIKANTHAM V，VATSALA A S.Basic theory of fractional differential equations[J].Nonlinear Analysis：Theory，Methods andApplications，2008，69：2677-2682.

[4]LAKSHMIKANTHAM V.Theory of fractional functional differential equations[J].Nonlinear Analysis：Theory，Methods andApplications，2008，69：3337-3343.

[5]AGARWAL R P，LAKSHMIKANTHAM V，NIETO J J. On the concept of solution for fractional differential equations with uncertainty[J].Nonlinear Analysis：Theory，Methods andApplications，2010，72：2859-2862.

[6]LI C，CHEN A，YE J.Numerical approaches to fractional calculus and fractional ordinary differential equation[J]. Journal of Computational Physics，2011，230：3352-3368. [7]MOROGADO M L，F(xiàn)ORD N J，LIMA P M.Analysis and numerical methods for fractional differential equationswith delay[J].Journal of Computational and Applied Mathematics，2013，252：159-168.

[8]ZHAO Y G，WANG Y Z，LIU Z B.Finite time stability analysis for nonlinear fractional order differential systems [C]//The 32ndChinese Control Conference.Xi’an：IEEE CPP，2013，487-492.

[9]LIAO Z，PENG C，LI W，WANG Y.Robust stability analysis for a class of fractional order systems with uncertain parameters[J].Journal of the Franklin Institute，2011，348：1101-1113.

[10]LI Y，CHEN Y，PODLUBNY I.Mittag-leffler stability of fractional order nonlinear dynamic systems[J].Automatica，2009，45：1965-1969.

[11]LI Y，CHEN Y，PODLUBNY I.Stability of fractional-order nonlinear dynamic systems：Lyapunov direct method and generalized Mittag-Leffler stability[J].Computers and Mathematics withApplications，2010，59：1810-1821.

[12]BOROOMAND A，MENHAJ M B.Fractional-order hopfield neural networks[J].Advances in Neuro-Information Processing，2009，5506：883-890.

[13]KASLIK E，SIVASUNDARAM S.Nonlinear dynamics and chaos in fractional-order neural networks[J].Neural Networks，2012，32：245-256.

[14]CHEN L，CHAI Y，WU R，et al.Dynamic analysis of a class of fractional-order neural networks with delay[J]. Neurocomputing，2013，111：190-194.

[15]ZOU T，QU J，CHEN L，et al.Stability analysis of a class of fractional-order neural networks[J].Telkomnika Indonesian Journal of Electrical Engineering，2014，12：1086-1093.

[16]MANUEL A DUARTE-MERMOUD，N AGUILA-CAMACHO，JAVIER A GALLEGOS，et al.Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems[J].Commun Nonlinear Science Numer Simulat，2015，22：650-659.

Global Asymptotically Stability of Fractional-Order Hopfield Neural Networks

CUI Shiweia,GAI Mingjiub,LIU Xiaoleib
（Naval Aeronautical and Astronautical University a.Graduate student’Brigade; b.Department of Basic Sciences,Yantai Shandong 264001,China）

In this paper,the global asymptotically stability of fractional-order hopfield neural networks was investigated, and a sufficient condition was given by using LMI approach.At last,a numerical example and corresponding numerical simulation were presented to demonstrate the effectiveness of the result.

fractional order;neural networks;asymptotically stability;LMI

O175.13

A

1673-1522（2015）05-0493-04

10.7682/j.issn.1673-1522.2015.05.019

2015-05-10；

2015-07-20

崔世維（1990-），男，碩士生。