具有時變權矩陣的離散Hopfield神經網絡的穩定性

周 剛，蓋明久，崔世維

（海軍航空工程學院a.基礎部；b.研究生管理大隊，山東煙臺264001）

具有時變權矩陣的離散Hopfield神經網絡的穩定性

周 剛a，蓋明久a，崔世維b

（海軍航空工程學院a.基礎部；b.研究生管理大隊，山東煙臺264001）

研究了以并行工作模式進行演化的具有時變連接權矩陣的離散Hopfield神經網絡，得到了判定網絡穩定的2個充分條件，改進了已有結果。

離散Hopfield神經網絡；連接權矩陣；對角占優矩陣；穩定性

1982 年，美國加州理工學院物理學家J.J.Hopfield教授開創性地提出了如下的離散神經網絡模型[1]：

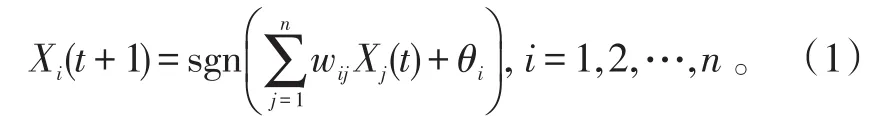
式（1）中：θi為閾值；wij為連接權重值；Xi取值-1或+1。

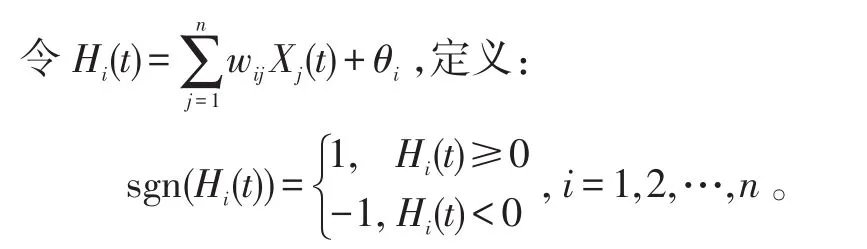
離散Hopfield神經網絡在模式識別、聯想記憶、圖像處理和組合優化等方面具有廣泛的應用[1-2]。由于在各種應用中都需要網絡穩定，因而離散Hopfield神經網絡的穩定性分析引起了人們的極大關注，并取得了眾多研究成果。而Hopfield在文獻[3]中引入的能量函數，是研究神經網絡穩定性的重要工具。

離散Hopfield神經網絡的工作演化方式有3種：串行方式、并行方式和部分并行方式。文獻[3-5]研究了連接權矩陣對稱且網絡在串行和并行方式下工作演化的穩定性；文獻[6-8]在此基礎上研究了權矩陣是非對稱情況下網絡穩定性；文獻[9]提出了部分并行演化方式，給出了一些穩定的條件；文獻[10-11]進一步研究網絡的不同工作演化方式，推廣了相關的結論；文獻[12]研究了連接權矩陣為時變情況下網絡的穩定性。

本文在文獻[11-12]的基礎上，研究具有時變連接權矩陣、以并行方式進行工作演化的離散Hopfield神經網絡，運用對角占優、廣義半正定等矩陣的性質給出其穩定性的充分條件，得到了一些新的結果。

1 預備工作

記X(t)=(X1(t),X2(t),…,Xn(t))T，θ=(θ1,θ2,…,θn)T，W(t)=(wij(t))n×n，則網絡（1）推廣到時變連接權形式：

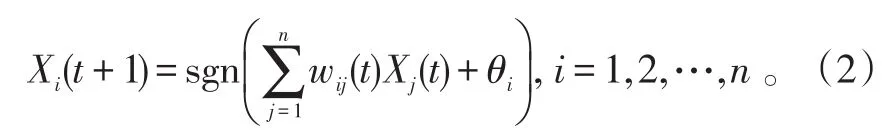
式（2）可寫成矩陣形式：

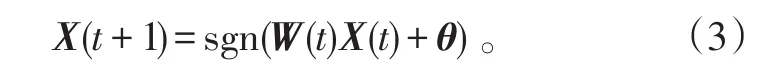
由式（2）可得，對于i=1,2,…,n，

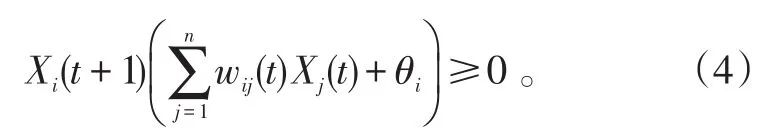
由于Xi(t)∈{-1,1}，且ΔXi(t)=Xi(t+1)-Xi(t)，所以ΔXi(t)∈{-2,0,2}。當 ΔXi(t)=-2時，Xi(t+1)=-1，Xi(t)=1，故Xi(t+1)ΔXi(t)≥0。再根據式（4），可得

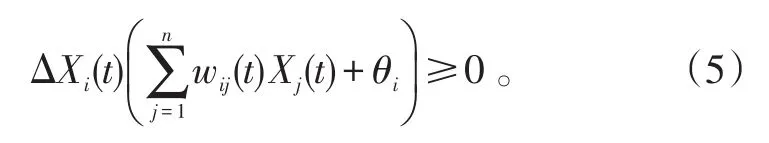
類似可以驗證，在各種取值情況下總有式（5）成立。于是有

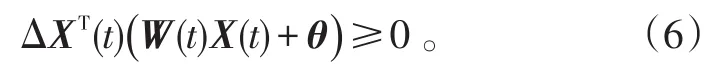
為研究神經網絡的穩定性，首先給出如下定義及引理。

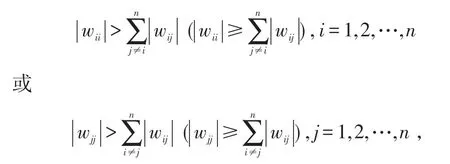
則稱W為嚴格行或列對角占優矩陣（W為行或列對角占優矩陣）。若W既是（嚴格）行對角占優又是（嚴格）列對角占優的，則稱W為（嚴格）對角占優矩陣。

若存在正對角矩陣P=diag(p1,p2,…,pn)，使得W滿足

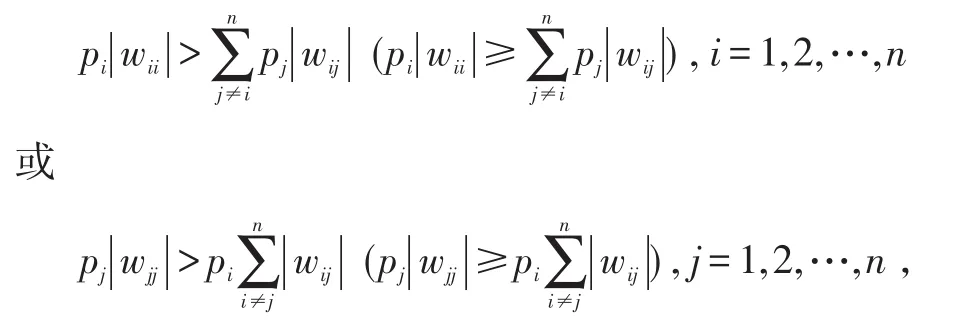
則稱W為廣義嚴格行或列對角占優矩陣（廣義行或列對角占優矩陣）。若W既是廣義（嚴格）行對角占優又是廣義（嚴格）列對角占優的，則稱W為廣義（嚴格）對角占優矩陣。

證明：不妨設W為廣義列對角占優的（W為廣義行對角占優的證明類似），則存在正對角矩陣P=diag(p1,p2,…,pn)，使得：

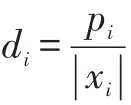
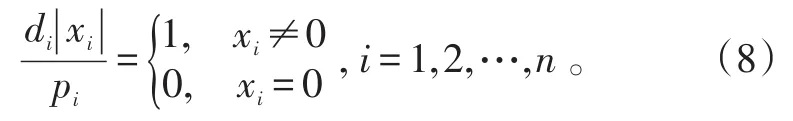
令Dx=diag(d1,d2,…,dn)，則

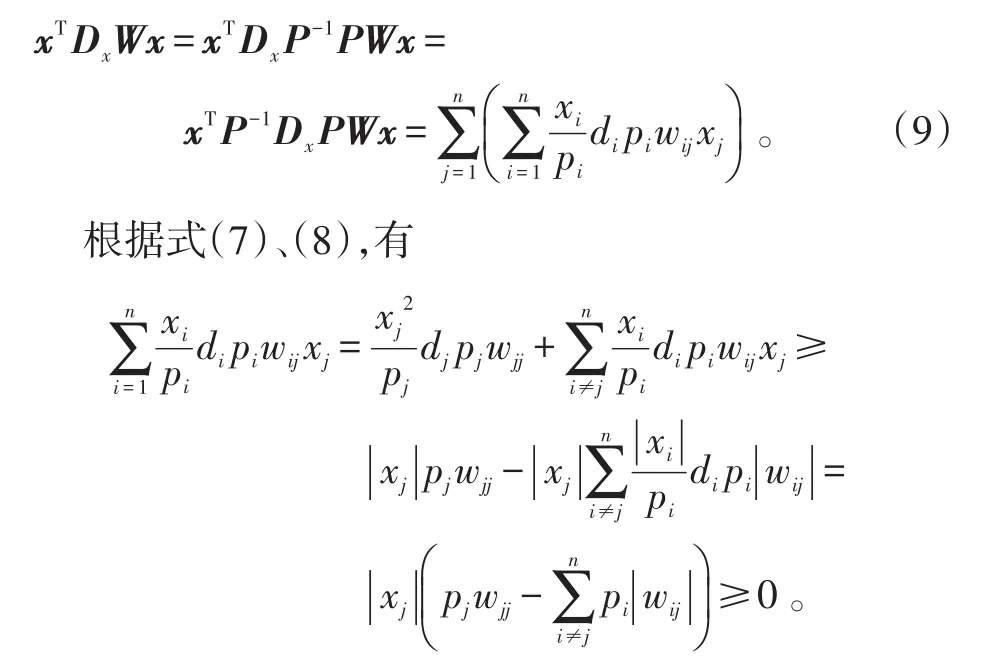
再由式（9）即得xTDxWx≥0，即W為廣義半正定矩陣。

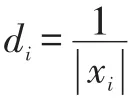
2 主要結果

定理：對于具有時變權矩陣函數的離散Hopfield神經網絡，如果W(t)=A(t)+B(t)+C(t)，并且滿足：

1）A(t)是廣義半正定矩陣，B(t)是廣義列對角占優矩陣，C(t)是廣義行對角占優矩陣；

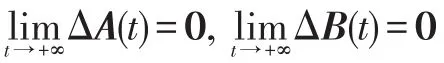
則神經網絡并行穩定。

證明：構造能量函數

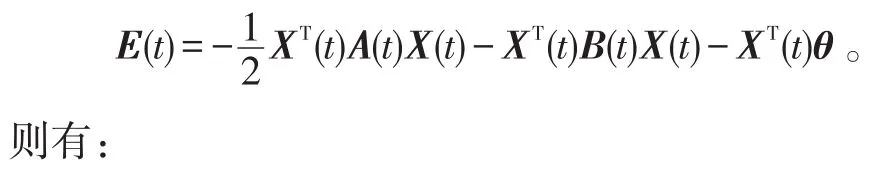
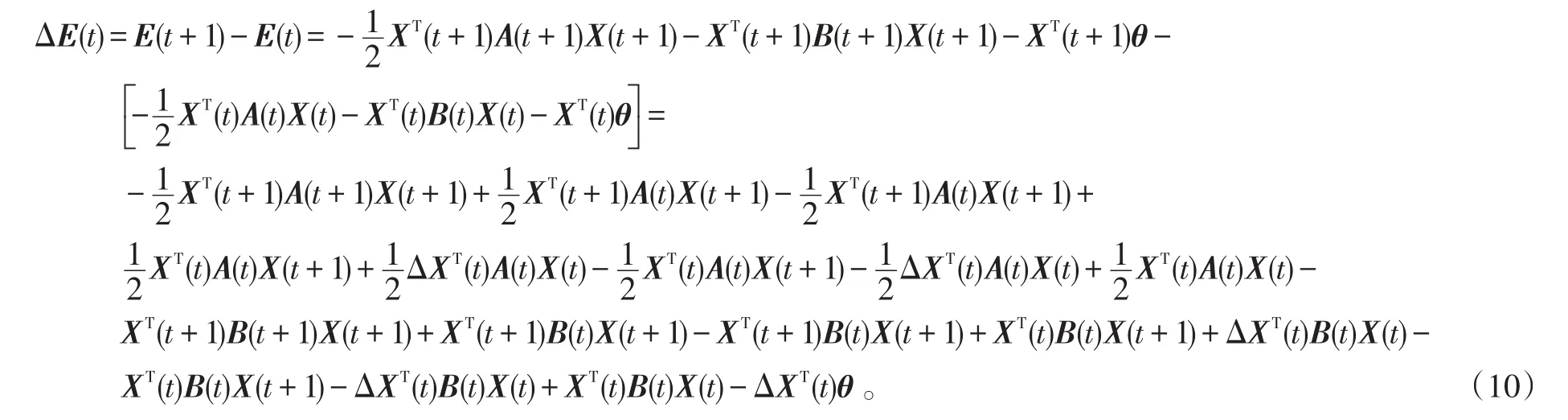
在式（10）的基礎上，引入含C(t)的項并整理得：

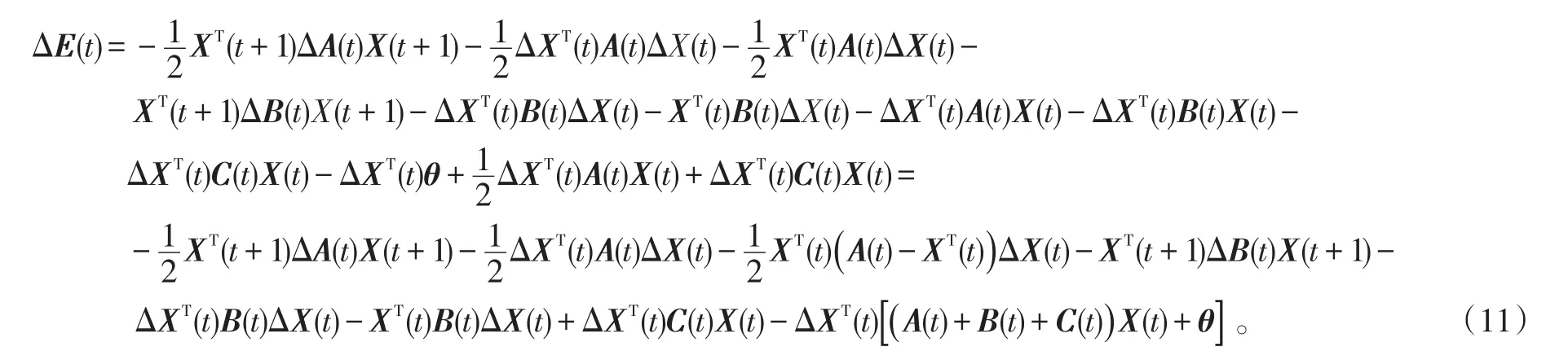
下面分2種情況討論分析。

1）當ΔX(t)=0時，根據式可知

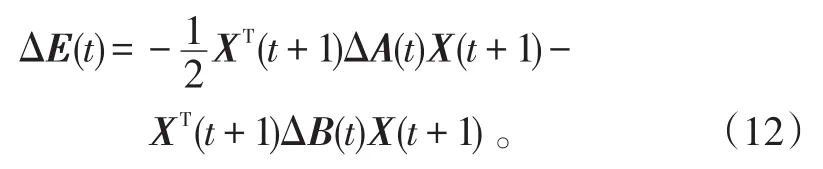
由于ΔA(t)、ΔB(t)為廣義行（或列）對角占優陣，不妨設ΔA(t)、ΔB(t)為廣義列對角占優的（ΔA(t)、ΔB(t)為廣義行對角占優的證明類似），所以分別存在正對角矩陣PΔA、PΔB，使定義2中的相應不等式成立。記：

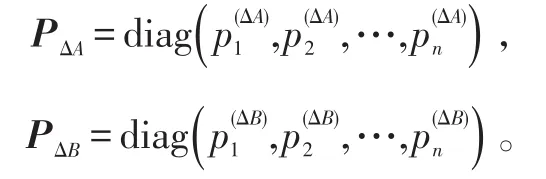
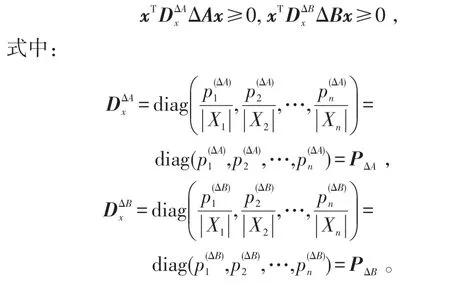
根據式（12），可得下式成立

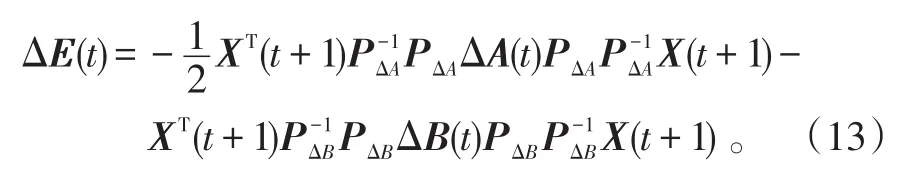
矩陣PΔAΔA(t)、PΔBΔB(t)為列對角占優，且、為正對角矩陣，所以仍為列對角占優。

進一步根據引理2可知存在 D1=D2=I（I為單位陣）使得是半正定的，即是半正定的。且又(P-1)T=P-1，則由式（13）可知：

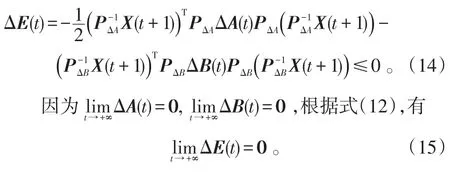
2）當 ΔX(t)≠0時，由于Xi(t)∈{-1,1}，且ΔX(t)=X(t+1)-X(t)，則

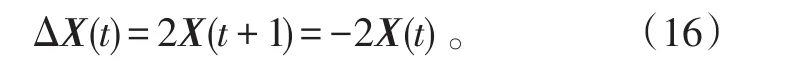
將式（6）、（16）代入式（11），可得

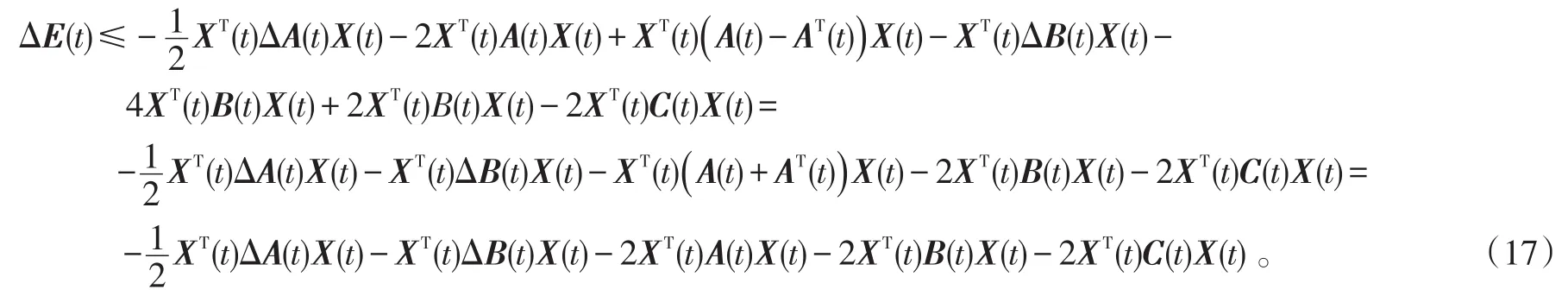
矩陣ΔA(t)、ΔB(t)都是廣義行（或列）對角占優矩陣，A(t)是廣義半正定矩陣，B(t)是廣義列對角占優矩陣，C(t)是廣義行對角占優矩陣，類似情形1）中的證明，由式（17）可得

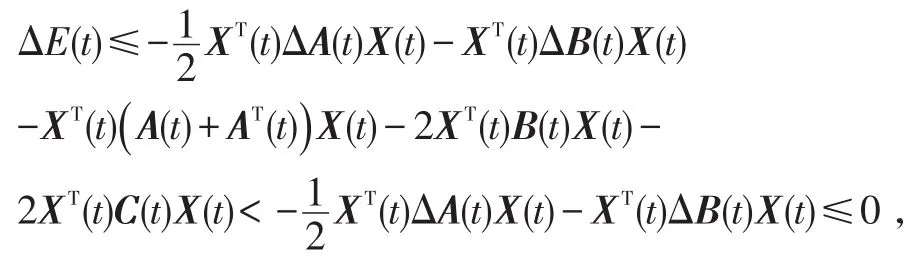
即

由式（14）、（18）及式（15）可知，神經網絡（2）是并行穩定的。

推論：對于具有時變權矩陣函數的離散Hopfield神經網絡，如果W(t)=A(t)+B(t)+C(t)，若

1）A(t)是正定矩陣，B(t)是列對角占優矩陣，C(t)是行對角占優矩陣；

3 結論

本文研究了在連接權值矩陣為時變情況下的離散Hopfield神經網絡并行工作演變的穩定性，得出了一些新的判定條件，改進了已有的結論。

[1]CHUA L O，YANG L.Cellular neural networks：applications[J].IEEE Transactions on Circuits and Systems，1988，35：1273-1290.

[2] LIU D.Cloning template design of cellular neural networks for associative memories.IEEE Transactions on Circuits and Systems—I：Fundamental Theory and Applications，1997，44：646-650.

[3] HOPFIELD J J.Neural networks and physical systems with emergent collective computational abilities[J].Proceedings of the National Academy of Science of the USA，1982，79（4）：2554-2558.

[4]GULES E，FOGELMAN F，PELLEGRINO D.Decreasing energy functions as a tool for studying threshod networks[J].Discrete Applied Mathematics，1985，12（3）：261-277.

[5]BRUCK J，GOODMAN J W.A generalized convergence theorem for neural networks[J].IEEE Transactions on Information Theory，1988，34（4）：1089-1092.

[6] CENUSCHI FIAS B.Partial simultaneous updating in Hopfield memories[J].IEEE Transaction on Systems，Man，and Cybernetics，1989，19（4）：887-888.

[7]XU Z B，KONG C P.Global convergence and asymptotic stability of asymmetric Hopfield neural networks[J].Journal of Mathematical Analysis and Applications，1995，191（3）：405-427

[8]廖曉昕，昌莉，沈軼.離散Hopfield神經網絡的穩定性研究[J].自動化學報，1999，25（6）：721-727. LIAO XIAOXIN，CHANG LI，SHEN YI.Study on stability of discrete-time Hopfield neural networks[J].Acta Automatica Sinica，1999，25（6）：721-727.（in Chinese）

[9]馬潤年，楊友社.離散Hopfield網絡的穩定性[J].空軍工程大學學報：自然科學版，2000，1（4）：39-41. MA RUNNIAN，YANG YOUSHE.The stability of discrete Hopfield networks[J].Journal of Airforce Engineering University：Natural Science Edition，2000，1（4）：39-41.（in Chinese）

[10]馬潤年，張強，許進.離散Hopfield神經網絡的穩定性研究[J].電子學報，2002，30（7）：1089-1091. MA RUNNIAN，ZHANG QIANG，XU JIN.Stability study of discrete Hopfield neural networks[J].Acta Electronica Sinica，2002，30（7）：1089-1091.（in Chinese）

[11]馬潤年，張強，許進.不同演化模式的離散Hopfield網絡的穩定性研究[J].系統工程與電子技術，2002，24（3）：90-94. MA RUNNIAN，ZHANG QIANG，XU JIN.Stability study on the discrete Hopfield network in various updating modes[J].Systems Engineering and Electronics，2002，24（3）：90-94.（in Chinese）

[12]LAI XIAOFENG，DIAO YONGFENG，LI MINGDONG，et al.Stability analysis of discrete Hopfield neural networks with quasi-diagonally dominant weight function matrix[C]//2010 International Colloquium on Computing，Communication，Control，and Management.Yangzhou，ISECS.2010：586-589.

Stability of Discrete Hopfield Neural Networks with Time-Variable Weighting Matrix

ZHOU Ganga,GAI Mingjiua,CUI Shiweib
（Naval Aeronautical and Astronautical University a.Department of Basic Science; b.Graduate Students’Brigade,Yantai Shandong 264001,China）

In this paper,a class of discrete Hopfield neural networks with variable weighting matrix in parallel update mode was studied.Several sufficient conditions were obtained to guarantee the stability of the neural networks.These re?sults improved and extended the existing results.

discrete Hopfield neural network;connection weight matrix;diagonally dominant matrix;stability

TP183

A

1673-1522（2015）05-0489-04

10.7682/j.issn.1673-1522.2015.05.018

2015-04-15；

2015-07-20

周 剛（1975-），男，副教授，碩士。