基于熵權“區別度”的導彈電子系統質量評估指標體系的優化

陳 勇，徐廷學，閆群章

（1.海軍航空工程學院兵器科學與技術系，山東煙臺264001；2.二炮裝備研究院，北京100085）

基于熵權“區別度”的導彈電子系統質量評估指標體系的優化

陳 勇1，徐廷學1，閆群章2

（1.海軍航空工程學院兵器科學與技術系，山東煙臺264001；2.二炮裝備研究院，北京100085）

基于熵權定義，分析了把熵權應用于指標賦權的不合理性，引出了熵權在指標可區別性上的價值度量。結合部隊實際需求，構建了基于“區別度”的優化模型，實現了指標在常規狀態和戰備狀態中的區別優化。并對導彈武器電子系統質量評估的指標進行了基于“區別度”的優化實例分析，驗證了算法的可行性及有效性。

熵權；區別度；質量評估；優化

導彈武器系統結構復雜，性能參數多，并且相互制約。而質量評估又具有交互性、動態性、環境多變性，以及人為因素性[1]。質量檢測主要依靠相關儀表、測試數據比對和專家經驗，不僅速度慢、周期長而且容易造成失誤，已遠遠不能滿足視情維修和實時評估的迫切需求[2]。

指標體系是進行質量評估工作的基礎和依據，并在一定程度上決定了導彈武器系統的信息采集乃至數據處理方式。因此，以導彈實測數據為基礎，選擇有代表性、獨立性、可比性、信息量大的指標是構建合理的、高效的評估指標體系的關鍵所在。

1 質量評估指標體系的建立

通過部隊調研得到的導彈故障數據分析可以看出，各類型導彈故障的特點有極大的相似之處，故障多發部件一般集中于導引頭、自動駕駛儀等電子部件。因此，導彈武器的電子系統測試結果決定了整個導彈武器系統的質量狀況，在質量檢測過程中占主導地位。本文質量評估指標體系正是建立在導彈武器電子系統整體測試基礎上進行的。

1.1 質量評估指標體系建立準則

1）系統性與獨立性相結合原則：導彈武器電子系統結構復雜，由諸多要素組成，評估指標應從系統的角度，綜合地反映導彈的整體情況，保證綜合評估的全面性與可信度。

2）定性與定量相結合原則：導彈武器電子系統的質量評估要求評估結果穩健可靠，在評估過程中，性能參數交織存在著精確與模糊、可測度與不可測度等多種情況，對整個系統的質量描述無法只用符號化、數量化的定量指標，應結合專家對定性指標的評判，通過信息融合技術，實現全面、準確的質量評估[3]。

3）動態與靜態相組合原則：軍事檢測和評估技術正不斷發展，評估指標體系要相應調整[4]，所選的指標也應該具有動態性與穩定性相結合的特點。因此，擔負質量檢測任務的部隊要與生產方和設計方建立信息反饋良性互動，使指標的建立在動態過程中反復平衡，確保評估指標能正確地反映導彈的質量狀況。

1.2 質量評估指標體系的建立

導彈武器電子系統是一個多因素的復雜系統，包含多種不確定因素。因此，在進行質量評估指標建立時，依據現有測試設備的測量指標[5]，把組成導彈武器電子系統的部、組件的指標建立作為重點，依據層次分析法將質量評估指標體系的因素集合劃分為3個層次：目標層A、準則層C與措施層D，本文不再贅述，可參考文獻[6]。

2 指標合理優化的重要意義

合理的指標優化對導彈武器電子系統質量評估有著重要的軍事意義。導彈武器電子系統待檢參數眾多，在常規評估過程中可以逐一檢測，進行全方位的性能維護，而在戰時情況下，選取信息量大、代表性強的指標可以縮短檢測時間，提高評估效率，為戰局主動贏得寶貴時間[7]。因此，實現評估指標在常規狀態和戰備狀態中的區別優化就顯得尤為重要。

作為導彈武器的核心部件，電子系統質量評估的指標體系要適應復雜環境下的軍事斗爭需要，從指標體系的建立到指標體系的優化應遵循一套科學的評審標準和步驟，堅持控制風險和規避風險的原則。導彈武器電子系統質量評估指標體系優化過程可以分為圖1所示的4大步驟。

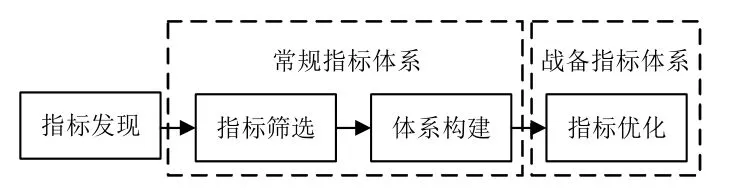
圖1 指標優化流程圖Fig.1 Flow chart of index optimization

3 基于熵權的“區別度”在指標優化中的應用

3.1 熵和熵權

熵原本是一熱力學概念，描述運動過程中的一個不可逆現象，后來在信息論中用熵來表示系統的紊亂程度，是系統不確定性或無序狀態的度量[8-9]。熵可以表示為

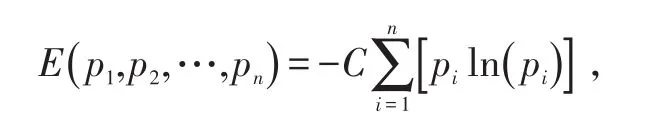
式中：C為常數；pi為相應概率。

若熵滿足以下條件：

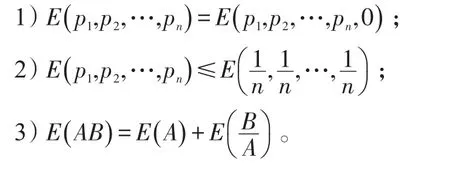
則熵有唯一表達形式：

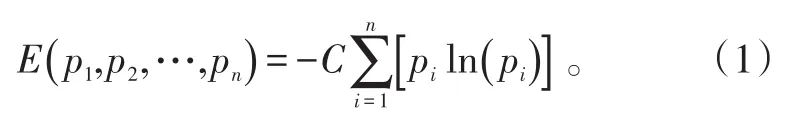
在信息論中，用有價值信息的多寡來權衡指標間的權重關系，這也表明了指標之間在“競爭”意義上的相對激烈程度，即熵權越大，熵值越小[8-9]，反之亦然。因此，可用信息熵所獲取系統信息的有序度確定指標權重，它可以剔除各指標權重計算時的人為因素干擾，使評估結果更客觀。

在具有m個評價指標，n個待評方案的評標問題（簡稱(m,n)評標問題）中，規范化矩陣為

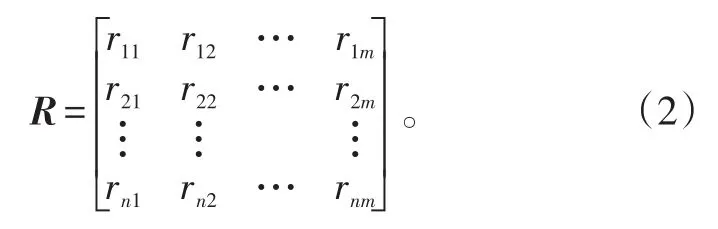
在導彈武器電子系統評估指標體系中，待評參數眾多，不同評價指標的綱量可能不同，這樣就不具有可比性。為了盡可能地反映實際情況，排除由于各項指標的單位不同，以及數值數量級間的懸殊差別所帶來的影響，避免不合理現象的發生，需要對評價指標作無量綱化處理。本文采用極值處理法對進行無量綱處理[10]，令，則

定義1（評價指標的熵）：在(m,n)評標問題中，第i個評價指標的熵定義為[11-12]：

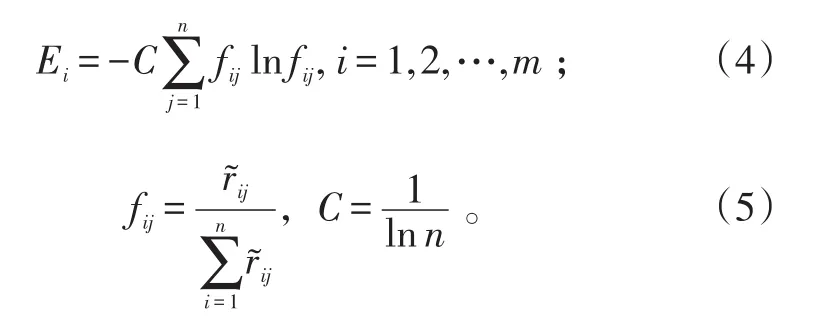
定義2（評價指標的熵權）：在(m,n)評標問題中，第i個評價指標的熵權定義為[12-13]：

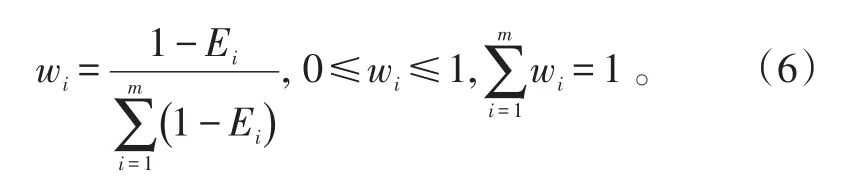
從上述熵和熵權定義可以得到如下結論：

1）當各待評價對象在指標上的取值相差較大則熵值較小，熵權越大，意味著該指標向決策者提供了有價值的信息。如果各對象在該指標上差異越明顯，則應重點關注。

2）當各待評價對象在指標上的值完全相同時，熵值達到最大值1，其熵權為0，說明該指標未向決策者提供任何有價值的信息，即在該指標下，所有備選項目對決策者都是無差異的，該指標可以被剔除。

3）評價指標的熵值和熵權呈反比關系。評價指標的熵值越小，其對應的熵權就越大，反之亦然。評價指標的熵值越大、熵權越小時，該指標對決策而言越不重要。

4）從信息論角度看，熵權代表該指標在該問題中提供有用信息量的多寡程度[8]。

5）作為權數的熵權，有其特殊意義。它并不是在評估或決策問題中某指標在實際意義上的重要性系數，而是在各種評價指標值均確定的情況下，各個指標在競爭意義上的相對激烈程度系數[14]。

3.2 指標體系優化模型構建

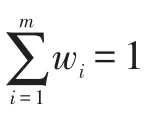
根據以上分析，現定義指標“區別度”η如下。

定義3（評價指標的“區別度”）：在(m,n)評標問題中，若第i個指標的熵值為Ei，熵權值為wi，則該指標的“區別度”可定義為：

根據以上指標“區別度”定義，本文針對導彈武器電子系統質量評估指標體系在優化過程中的實際應用進行了可行性分析。

1）符號分析。在定義(m,n)評標問題中，m代表評價指標的個數，n代表評價方案的個數；而在導彈武器電子系統質量評估指標體系優化中，m代表同一層次下待優化導彈性能指標的個數，n代表待優化指標的導彈武器全壽命周期內歷史檢測次數。通過這一轉換后就可以實現模型優化的“對號入座”。

2）變量分析。在導彈武器電子系統質量評估的指標評價體系構建的過程中，不可能出現某個指標的熵值Ei=1或Ei=0的情況。若Ei=1，意味著該指標對被評估對象沒有提供有價值信息；若指標熵值Ei=0，意味著只需要一個指標就能夠提供全部的信息量。以上2種情況是不符合實際情況的，故“區別度”的計算公式都是有意義的。

3）標準分析。要想進一步實現對評價指標的合理優化，必須依據“區別度”來制定相應的優化標準。根據導彈武器質量評估中可接受的最低可檢指標率是0.6[15]，可通過各個指標的“區別度”值實現同一層次指標的排序，并以導彈武器電子系統同一層次指標的60%進行優化篩選。

4）比較分析。若指標“區別度”和“重要度”趨于一致，則該指標對評估對象不僅很重要，而且具有非常強的區別能力，這樣的指標必然最理想。

5）區別分析。在武器電子系統中，依據地測設備所建立的指標為常規指標，而通過“區別度”優化后的指標稱為戰備指標。實行指標區別優化后，就可以對導彈武器電子系統實現平時細測全面評估，戰時粗測重點評估，為日常保養和把握戰機提供可靠保證。

綜上所述，假設在導彈武器電子系統某一層次評估指標體系的構建過程中，有m個初評指標，對此已進行了n次測量（n包括歷史測量和當前測量），在“區別度”測度下，需要對指標進行優化篩選，將指標數量減少到C(C＜m)個，具體步驟如式（1）～（6），再根據“區別度”值進行排序，選取排在前面的C個指標，組成戰備指標庫。

4 算例分析

假設某型導彈先后共進行了4次全面檢測，共包含了大約347個測試參數，若是對每個測試參數都進行分析不僅費時費力，而且也是不科學的。為了加強研究的針對性，基于從調研得到的導彈故障數據，請導彈各專業的專家對導彈易故障部件所對應的關鍵測試參數進行了分析確定，本文選取了對某型導彈雷達系統共計4次檢測的10個性能參數進行了分析，指標的范圍分別是指標1本振（4.6～5.4V）、指標2電壓（26.5～30.5V）、指標3航控電壓（9.2～10.8V）、指標4磁控管電流（8.5～14.5A）、指標 5距離輸出 1（14.7～15.3km）、指標6距離輸出2（8.7～9.3km）、指標7捕捉靈敏度（86～100dBm）、指標8距離跟蹤下限（10.5～12.5μs）、指標9探測脈沖位置（9.5～10.5μs）、指標10STC衰減（2.5～9.5dB）如表1所示。

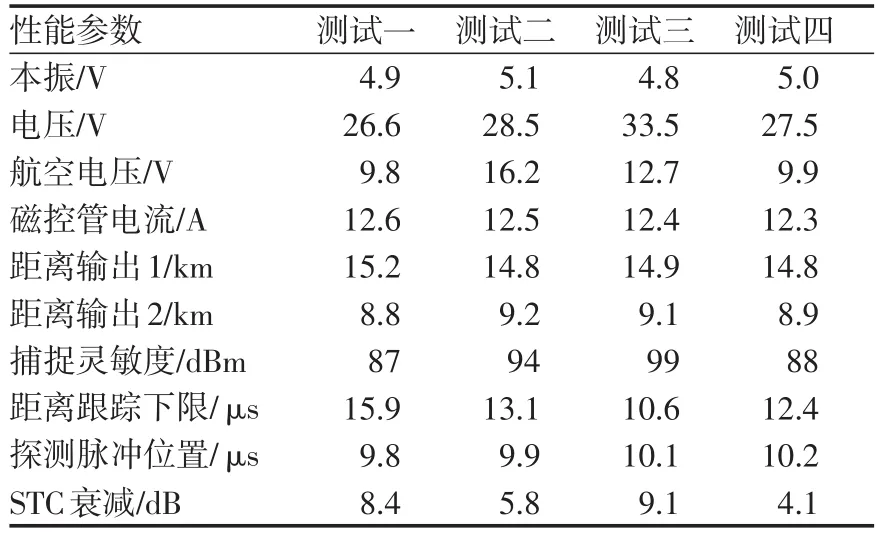
表1 某型導彈雷達系統性能檢測指標數據Tab.1 Performance test index data of a missile radar system

指標優化的計算步驟如下：

2）根據式（4）計算每個指標熵值Ei得：

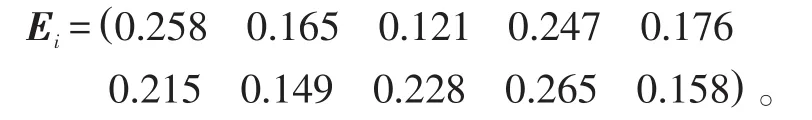
3）根據式（6）計算每個指標熵權值wi得：

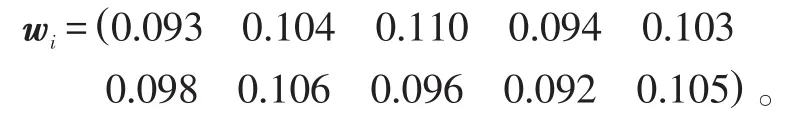
4）根據式（7）計算每個指標“區別度”ηi得：

5）對“區別度”值ηi由大至小進行排序見表2。

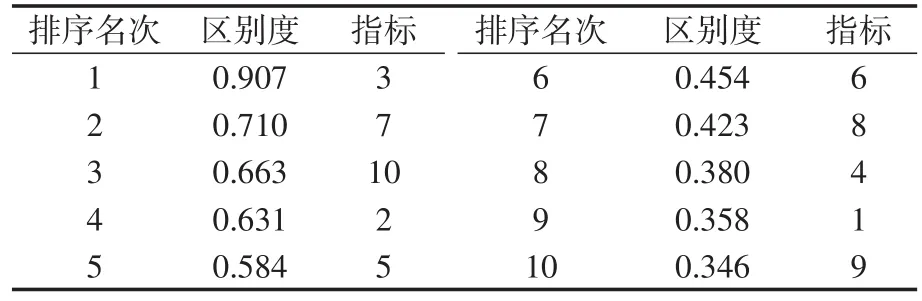
表2 對“區別度”排序Tab.2 Sorting of‘distinction’

6）優化分析，實現常規指標與戰備指標的區分。依據武器最低可檢指標率和“區別度”值排序，指標9、指標1、指標4的“區別度”測度值低（穩定性強），可從常規指標中剔除，從而實現指標在常規狀態和戰備狀態下的優化區分。根據相應導彈專家所指，指標9相對于影響導彈雷達整體質量的重要程度要高于指標8和指標6，但是同一型號導彈經過4次測試后，指標9的穩定程度高于指標8和指標6，那么在戰備狀態下，我們可以對此型號導彈免于檢測指標9，縮短整彈測試時間，以利于更好的把握戰場時機。

通過區別度的量化，在同一坐標系中，實現了相對熵權值的放大，如圖2所示。

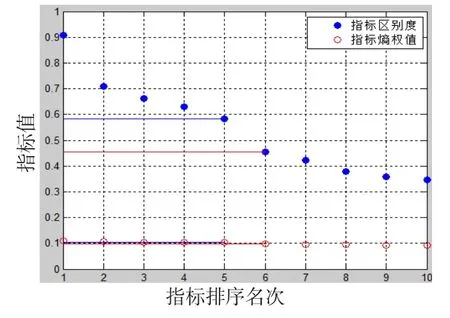
圖2 “區別度”放大Fig.2 Amplification of‘distinction’

在“區別度”排序前，第5名和第6名對應的指標值幾乎重疊了，而經過“區別度”排序后，第5名和第6名之間的區分就非常明顯了，其他排名也同樣如此。算例中只是針對了10個指標，效果還不是很明顯。如果指標非常多，就很有可能出現指標熵權值過于集中，不利于區別。此算法從某種程度上擴大了指標間的差距，更利于對指標間的權衡分析。

對導彈武器電子系統，因其由大量電子元器件及芯片集成，故元器件老化、功能退化等不穩定因素很多。因此，測量值波動大的指標對系統性能的影響尤為突出，也必然成為檢測的重點指標，即戰備指標，而指標“區別度”則恰恰能實現對上述指標的辨別。

算例只是應用優化模型對某型導彈雷達系統經過4次測試的10個性能指標進行了優化分析，此算法完全可以應用于整彈電子系統各個層次下的性能指標優化。對于指標的個數m以及測試的次數n沒有具體要求，當然檢測次數n越大，檢測結果的可信度就越高。另外，此算法已經利用Matlab編寫了通用程序，驗證了算法的可行性和通用性。

綜上所述，基于“區別度”的測度模型實現了武器電子系統的指標優化，作為在同一層次下“區別度”值較低的指標9、指標1、指標4，其測量值的穩定反映了與之相關的電子元件的穩定，這也與在部隊調研時的結果相吻合。因此，用除去指標9、指標1、指標4外的7個指標作為戰備指標是合理的。

5 小結

本文以導彈武器電子系統質量評估指標體系優化作為理論研究的背景，介紹了指標體系建立的通用準則，結合指標優化的實際意義，從熵權的角度出發，引出熵權在指標可區別性上的價值度量。結合部隊需求，構建了基于“區別度”的優化模型，實現了指標在常規狀態和戰備狀態中的區別優化。對導彈武器電子系統某一層次質量評估的指標進行了基于“區別度”的優化實例分析，驗證了算法的可行性及有效性。

[1]王軍延，劉維國，汪菲.某型導彈武器系統效能評估方法應用研究[J].艦船電子工程，2010，30（9）：54-57. WANG JUNYAN，LIU WEIGUO，WANG FEI.Efficiency evaluation method researching for missile weapon system[J].Ship Electronic Engineering，2010，30（9）：54-57.（in Chinese）

[2]梁旭，李行善，張磊.支持視情維修的故障預測技術研究[J].測控技術，2007，26（6）：5-8. LIANG XU，LI XINGSHAN，ZHANG LEI.Survey of fault prognostics supporting condition based maintenance [J].Measurement&Control Technology，2007，26（6）：5-8.（in Chinese）

[3]李恩友.導彈質量評估方法研究[J].彈箭與指導學報，2008，28（4）：79-82. LI ENYOU.Research of missile quality evaluation methods[J].Journal of Projectiles，Rockets，Missiles and Guidance，2008，28（4）：79-82.（in Chinese）

[4]張永久.多型號導彈質量評估系統設計[J].航空兵器，2005，4（2）：29-32. ZHANG YONGJIU.The quality evaluation system for different missiles[J].Aero Weaponry，2005，4（2）：29-32.（in Chinese）

[5]田錫惠，徐浩.導彈結構、材料、強度[M].北京：宇航出版社，1996：15-83. TIAN XIHUI，XU HAO.Missile structure，material，strength[M].Beijing：Space Press，1996：15-83.（in Chinese）

[6]王蓮芬.層次分析法引論[M].北京：中國人民大學出版社，1990：11-156. WANG LIANFEN.Introduction of analytic hierarchy process[M].Beijing：China Renmin University Press，1990：11-156.（in Chinese）

[7]史本山，楊季美.關于評價指標集并理論和方法的研究[J].西南交通大學學報，1991，10（8）：74-80. SHI BENSHAN，YANG JIMEI.Research on evaluation index set theory and method[J].Journal of Southwest Jiaotong University，1991，10（8）：74-80.（in Chinese）

[8]ALADDIN SHAMILOV，CIGDEM GIRIFTINOGLU. Generalized entropy optimization distributions dependent on parameter in time series[J].WSEA Transactions on Information andApplication，2010,7（1）：102-111.

[9]周曉光.基于熵權的模糊物元決策[J].系統管理學報，2009，18（4）：444-458. ZHOU XIAOGUANG.Research on method of vague matter-element decision making based on entropy weight[J]. Systems Engineering-Theory Methodology Application，2009，18（4）：444-458.（in Chinese）

[10]李明奇，劉玉娟.一種基于判斷矩陣的專家賦權方法[J].科技信息，2010，11（21）：45-47. LI MINGQI，LIU YUJUAN.Expert weighting method based on judgment matrix[J].Science&Technology Information，2010，11（21）：45-47.（in Chinese）

[11]HWANG C L，YOON K S.Multiple attribute decision making[M].Berlin：Spinger Verlag，1981：29-56.

[12]黃文忠，艾凌云，彭博.基于熵權和理想解法的炮兵陣地優選方法[J].艦船電子工程，2010，30（8）：45-47. HUANG WENZHONG，AI LINGYUN，PENG BO. Methodology to artillery position option based on entropy weighting and TOPSIS[J].Ship Electronic Engineering，2010，30（8）：45-47.（in Chinese）

[13]YOUNGPIL C，MOOYOUNG J.Satisfaction assessment of multi objective schedules using neural fuzzy methodology[J].International Journal of Production Research，2003，41（8）：1831-1849.

[14]SOROOSH S，FAZEL ZARANDI M H.A comprehensive fuzzy multi objective model for supplier selection process [C]//Proceedings IEEE InternationalConference on Fuzzy Systems.St.Louis，MO：IEEE，2003：256-271.

[15]張永久，成躍，張立新.某型導彈質量評估方法研究[J].航空兵，2007，10（5）：56-59. ZHANG YONGJIU，CHENG YUE，ZHANG LIXIN.Research of quality evaluation methods for certain missile [J].Aero Weaponry，2007，10（5）：56-59.（in Chinese）

Optimization of Indicator System about Quality Evaluation for Missile Electric System Based on Entropy Weigh‘Distinction’

CHEN Yong1,XU Tingxue1,YAN Qunzhang2
（1.Department of Ordnance Science and Technology,NAAU,Yantai Shandong 264001,China; 2.Institute of Second Artillery,Beijing 100085,China）

Based on the definition of entropy weight,the irrationality of applying entropy weight to the index weight was an?alyzed,and the measurement value of entropy weight in distinguishability was introduced.Combined with the actual de?mand of troops,the optimization model which was based on the‘distinction’was constructed,and the distinguishing opti?mization about index between normal state and readiness posture was achieved.Index for quality evaluation of missile elec?tric system was analyzed in optimization example which was based on‘distinction’,and the feasibility and effectiveness of the algorithm were verified.

entropy weight;distinction;quality evaluation;optimization

TJ760

A

1673-1522（2015）05-0484-05

10.7682/j.issn.1673-1522.2015.05.017

2015-06-10；

2015-07-22

陳 勇（1984-），男，碩士生。