低噪聲風(fēng)力機(jī)翼型設(shè)計(jì)方法及實(shí)驗(yàn)分析

汪泉，陳進(jìn)，程江濤，3，王君，孫金風(fēng)，游穎

(1.湖北工業(yè)大學(xué) 機(jī)械工程學(xué)院，武漢430068;2.重慶大學(xué) 機(jī)械工程學(xué)院，重慶400030;3.丹麥技術(shù)大學(xué) 機(jī)械工程學(xué)院，靈比DK－2800)

風(fēng)能是一種綠色可再生能源，取之不盡，用之不竭，隨著風(fēng)力機(jī)的迅速發(fā)展與應(yīng)用，風(fēng)輪尺寸越來(lái)越大，運(yùn)行過(guò)程中產(chǎn)生的噪聲也越來(lái)越嚴(yán)重，對(duì)周?chē)肼暛h(huán)境的影響也受到人們的廣泛關(guān)注.按照不同聲源風(fēng)力機(jī)噪聲可分為機(jī)械噪聲和氣動(dòng)噪聲.由于目前的機(jī)械制造水平及技術(shù)的不斷提高，機(jī)械噪聲可以較好的控制，而降低風(fēng)力機(jī)的氣動(dòng)噪聲成為目前研究的關(guān)鍵問(wèn)題.風(fēng)力機(jī)的氣動(dòng)噪聲按照噪聲產(chǎn)生的機(jī)理可分為低頻噪聲、來(lái)流噪聲和翼型自身噪聲3種［1］.美國(guó)可再生能源實(shí)驗(yàn)室的 Brooks等［2］在總結(jié) NACA－0012 翼型噪聲風(fēng)洞實(shí)驗(yàn)的基礎(chǔ)上，提出了一種半經(jīng)驗(yàn)的風(fēng)力機(jī)翼型噪聲計(jì)算模型(簡(jiǎn)稱BPM模型).該模型計(jì)算速度和精度可滿足工程實(shí)際需求，是目前翼型噪聲計(jì)算使用最廣泛的方法之一.Zhu等［3］基于這種半經(jīng)驗(yàn)公式，引入動(dòng)量葉素理論，考慮翼型的邊界層特性，提出了一種適用于風(fēng)力機(jī)翼型的修正經(jīng)驗(yàn)?zāi)Ｐ停⑴c實(shí)驗(yàn)結(jié)果對(duì)比從而驗(yàn)證了該模型的準(zhǔn)確性.司海青等［4］研究了數(shù)值預(yù)測(cè)風(fēng)力機(jī)氣動(dòng)噪聲的一種半經(jīng)驗(yàn)?zāi)Ｐ停⒂?jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)進(jìn)行了對(duì)比，從而驗(yàn)證半經(jīng)驗(yàn)?zāi)Ｐ偷挠行?余雷等［5］采用非線性計(jì)算氣動(dòng)聲學(xué)方法和基于雷諾平均NS方程計(jì)算流體力學(xué)方法對(duì)常規(guī)后緣風(fēng)力機(jī)翼型及其修型后的鈍后緣翼型的氣動(dòng)噪聲進(jìn)行了計(jì)算，并討論了這兩種計(jì)算方法不同的數(shù)值模擬能力.Singh等［6］針對(duì)小型風(fēng)力機(jī)翼型，設(shè)計(jì)出了低雷諾數(shù)條件下的新型翼型，并將數(shù)值計(jì)算與風(fēng)洞實(shí)驗(yàn)進(jìn)行了對(duì)比，揭示其流動(dòng)機(jī)理.然而，以上研究均是對(duì)已有翼型進(jìn)行噪聲特性研究，很少有對(duì)低噪聲翼型進(jìn)行優(yōu)化設(shè)計(jì)及噪聲實(shí)驗(yàn)驗(yàn)證;雖然風(fēng)力機(jī)翼型的數(shù)值計(jì)算及實(shí)驗(yàn)驗(yàn)證的相關(guān)研究較多［7－13］，且研究成果顯著，但是缺乏相關(guān)的噪聲研究及實(shí)驗(yàn)驗(yàn)證.

因此，本文基于翼型泛函集成理論及翼型噪聲計(jì)算模型，將RFOIL與BPM模型耦合求解翼型噪聲特性;提出以升阻比與噪聲比值為設(shè)計(jì)目標(biāo)函數(shù)，建立低噪聲風(fēng)力機(jī)翼型優(yōu)化數(shù)學(xué)模型，對(duì)優(yōu)化后的新翼型進(jìn)行氣動(dòng)性能與噪聲實(shí)驗(yàn)研究;為了驗(yàn)證新翼型具有較低的噪聲特性，在相同的噪聲風(fēng)洞實(shí)驗(yàn)及風(fēng)速條件下，與風(fēng)力機(jī)常用NACA－64－618翼型進(jìn)行噪聲對(duì)比分析并給出結(jié)果評(píng)價(jià).

1 翼型噪聲計(jì)算模型

基于Brooks等［2］的計(jì)算模型(簡(jiǎn)稱 BPM 模型)，翼型自身噪聲可分為:尾緣噪聲(TBL－TE)、葉尖噪聲(TIP)、失速噪聲(SEP)、鈍尾緣噪聲(TEB－VS)、層流渦噪聲(LBL－VS)［3，14］.而一般情況下，翼型自身的噪聲主要源于尾緣噪聲和失速噪聲，因此本文主要介紹這兩種噪聲計(jì)算公式.

1.1 湍流邊界層尾緣噪聲(TBL-TE)

當(dāng)附著在葉片上的湍流邊界層流經(jīng)尾緣與尾緣相互作用就會(huì)產(chǎn)生湍流邊界層尾緣噪聲.在一定的攻角和雷諾數(shù)下，在翼型表面的某個(gè)位置層流會(huì)發(fā)生轉(zhuǎn)捩變成湍流，而湍流會(huì)在尾緣的壓力面和吸力面產(chǎn)生波動(dòng)的壓力，導(dǎo)致噪聲的產(chǎn)生.在攻角較小時(shí)，壓力面和吸力面的噪聲是主要的噪聲源［15］.

湍流邊界層尾緣噪聲SPL1是由湍流邊界層在壓力面產(chǎn)生的噪聲SPLp與在吸力面產(chǎn)生的噪聲SPLs之和［14］:

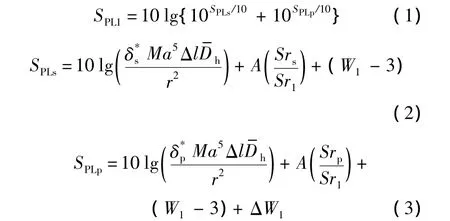
其中，尾緣噪聲表示成關(guān)于吸力面尾部邊界層相對(duì)厚度δ*s和壓力面尾部邊界層相對(duì)厚度δ*p的函數(shù)，與翼型的攻角α和來(lái)流的雷諾數(shù)Re有關(guān);Ma為來(lái)流的馬赫數(shù)，是來(lái)流相對(duì)速度U與音速c0的比值;Sr為斯特勞哈爾數(shù)，Srs和Srp分別為吸力面和壓力面的斯特勞哈爾數(shù)，Sr1為尾緣噪聲的斯特勞哈爾基數(shù);為高頻聲音方向函數(shù);r為觀察者距離聲源距離;A為頻譜形狀函數(shù);W1為振幅函數(shù);ΔW1為聲壓級(jí)修正函數(shù);Δl為翼型沿展向長(zhǎng)度.

1.2 失速噪聲(SEP)

當(dāng)攻角增大時(shí)，邊界層會(huì)發(fā)生分離，吸力面區(qū)域的湍渦會(huì)比低攻角時(shí)更大，當(dāng)湍渦變成尾跡，進(jìn)而產(chǎn)生分離流噪聲.隨著攻角增大到一定程度，邊界層發(fā)生大規(guī)模分離，翼型完全失速，此時(shí)失速噪聲為最主要噪聲:

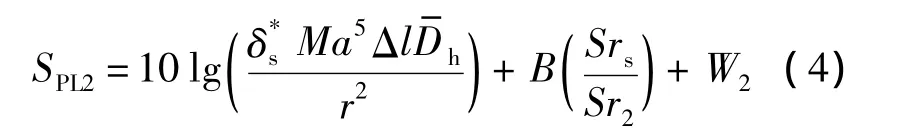
式中，B為頻譜形狀函數(shù);W2為振幅函數(shù).

2 翼型型線設(shè)計(jì)理論

基于翼型泛函集成理論［13］，翼型廓線在二維平面坐標(biāo)方程可表示為

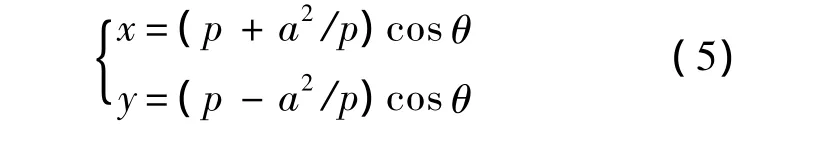
式中，a為0.25倍翼型的弦長(zhǎng);p為翼型的矢徑長(zhǎng)度，可表示為

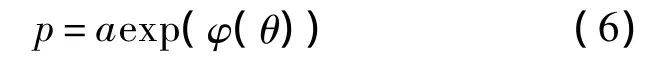
根據(jù)三角級(jí)數(shù)思想，翼型形函數(shù)可表示為

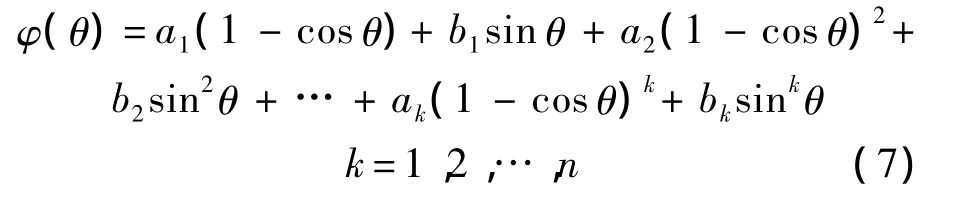
將式(6)、式(7)代入式(5)，選取不同的級(jí)數(shù)系數(shù)k，ak，bk，就可表示多種形狀的翼型.

3 低噪聲風(fēng)力機(jī)翼型設(shè)計(jì)模型

隨著風(fēng)力機(jī)的大型化，噪聲也越來(lái)越大，因此有必要設(shè)計(jì)低噪聲翼型，從而降低風(fēng)力機(jī)的噪聲.翼型自身噪聲與一定雷諾數(shù)及攻角條件下翼型尾緣上下表面邊界層厚度密切相關(guān)，通過(guò)控制翼型表面邊界層厚度就可以控制翼型的噪聲.本文中翼型的邊界層參數(shù)通過(guò)RFOIL軟件計(jì)算，將翼型的參數(shù)方程與RFOIL耦合求解，在優(yōu)化過(guò)程中計(jì)算翼型的氣動(dòng)特性及壓力面和吸力面的邊界層厚度，從而控制翼型的氣動(dòng)性能及噪聲值.

3.1 目標(biāo)函數(shù)

翼型性能考慮的因素很多，除了低噪聲之外，還包括氣動(dòng)、結(jié)構(gòu)等不同學(xué)科的要求.本文主要考慮翼型具有較高的氣動(dòng)性能及較低的噪聲大小，建立了以升阻比與噪聲值的比值為目標(biāo)函數(shù)的數(shù)學(xué)模型:

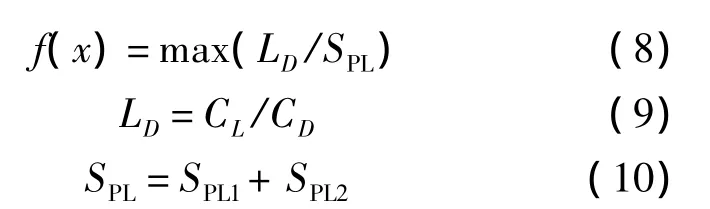
式中，CL為翼型的升力系數(shù);CD為翼型的阻力系數(shù);LD為翼型在設(shè)計(jì)攻角下的升阻比;SPL為翼型在設(shè)計(jì)攻角下的噪聲，這里設(shè)計(jì)攻角為6°.

3.2 設(shè)計(jì)變量和約束

對(duì)于翼型廓線的泛函集成方程，選擇式(7)的前6項(xiàng)系數(shù)為優(yōu)化設(shè)計(jì)變量:

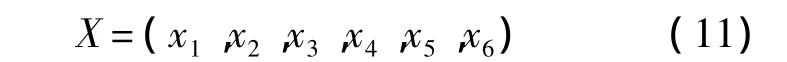
式中變量的變化空間根據(jù)翼型的形狀來(lái)確定，為了型線具有翼型的特征，對(duì)變量進(jìn)行如下約束:

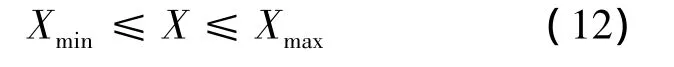
除了對(duì)形狀的要求以外，還得考慮翼型的結(jié)構(gòu)兼容性問(wèn)題.其中翼型的厚度及其所處的位置是結(jié)構(gòu)兼容性兩個(gè)主要的參數(shù)，本文選取最大相對(duì)厚度為0.18的翼型進(jìn)行優(yōu)化設(shè)計(jì)，施加厚度及其位置約束為

其中，t為翼型的最大相對(duì)厚度;c為翼型的弦長(zhǎng).

3.3 優(yōu)化結(jié)果

基于翼型泛函集成理論與噪聲計(jì)算模型，結(jié)合翼型優(yōu)化模型，選取初始條件為:雷諾數(shù)Re=2.0×106，當(dāng)?shù)仫L(fēng)速 V0=70 m/s，觀察者的距離r=1 m，觀察角度為90°，c=1 m，翼展長(zhǎng)度為1 m，得到一種風(fēng)力機(jī)新翼型CQU－DTU－B18，新翼型的輪廓型線如圖1所示.

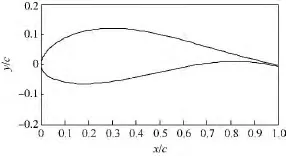
圖1 CQU－DTU－B18 翼型廓線Fig.1 CQU－DTU－B18 airfoil profile

4 實(shí)驗(yàn)驗(yàn)證

為了驗(yàn)證翼型的氣動(dòng)性能，聯(lián)合丹麥技術(shù)大學(xué)一起做了該新型翼型的風(fēng)洞實(shí)驗(yàn)，該實(shí)驗(yàn)內(nèi)容是在丹麥RISΦ實(shí)驗(yàn)室完成的.翼型攻角范圍為－5°～20°，實(shí)驗(yàn)雷諾數(shù)為 Re=2.0 ×106，馬赫數(shù)為0.15，實(shí)驗(yàn)結(jié)果與RFOIL計(jì)算結(jié)果如圖2和圖3所示.

由圖2和圖3可知:實(shí)驗(yàn)測(cè)試最大升力系數(shù)為1.777，出現(xiàn)在攻角為11°的位置，而RFOIL計(jì)算最大升力系數(shù)為1.919，出現(xiàn)在攻角為12°的位置，誤差較小為7.991%;實(shí)驗(yàn)測(cè)試最大升阻比為142.3，出現(xiàn)在攻角為6°的位置，RFOIL計(jì)算最大升阻比為144.9，出現(xiàn)在攻角為7°的位置，誤差僅為1.833%，表明風(fēng)洞實(shí)驗(yàn)值與RFOIL計(jì)算結(jié)果吻合得較好.從而驗(yàn)證了新翼型具有優(yōu)良的氣動(dòng)性能.

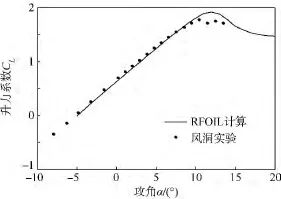
圖2 升力系數(shù)RFOIL計(jì)算與實(shí)驗(yàn)結(jié)果的對(duì)比Fig.2 Comparison of the experimental results and the RFOIL predicted lift coefficient

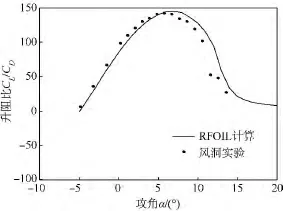
圖3 升阻比RFOIL計(jì)算與實(shí)驗(yàn)結(jié)果的對(duì)比Fig.3 Comparison of experimental results and the RFOIL predicted lift/drag ratio

為了驗(yàn)證新翼型具有較低的噪聲性能，下面重點(diǎn)研究新翼型噪聲特性，并將噪聲實(shí)驗(yàn)結(jié)果與同等條件下常用翼型NACA－64－418翼型噪聲實(shí)驗(yàn)結(jié)果進(jìn)行對(duì)比分析.噪聲測(cè)試段及消音室如圖4所示，翼型噪聲實(shí)驗(yàn)?zāi)Ｐ拖议L(zhǎng)為0.6 m，展向長(zhǎng)度為1.62 m.觀察者距離翼型實(shí)驗(yàn)段的距離為1.62 m，觀察角度為90°.該模型安裝有62個(gè)壓力孔，全部由鋁塊制造而成.噪聲原始數(shù)據(jù)由傳音器測(cè)試而來(lái)，并通過(guò)頻域波束形成技術(shù)進(jìn)行處理.該技術(shù)能夠從背景噪聲中提取聲壓值.時(shí)間序列可以通過(guò)在32 s期間以51.2 kHz的采樣頻率進(jìn)行測(cè)量，并分成200塊，8 192個(gè)樣本用以計(jì)算平均的交叉譜密度矩陣.考慮3種不同的風(fēng)速工況，分別為30，45及60 m/s.由于這兩種翼型在0°攻角情況下的升力系數(shù)及失速攻角均有較大差別，因此很難比較他們的噪聲大小.而翼型的升力系數(shù)與升阻比是構(gòu)建風(fēng)力機(jī)葉片的主要性能，因此本文比較在相同升力系數(shù)情況下的噪聲特性.

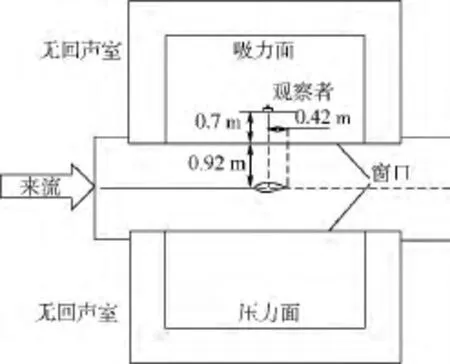
圖4 翼型噪聲測(cè)試示意圖Fig.4 Schematic of airfoil noise test section

圖5(a)和圖5(b)分別為風(fēng)速為30 m/s，CL=0.52 和 CL=0.95 時(shí) CQU－DTU－B18 翼型與NACA－64－618翼型的聲壓級(jí)對(duì)比圖.研究表明:相比 NACA－64－618 翼型，在頻率低于3 kHz時(shí)，新翼型具有較低的噪聲值;相比實(shí)驗(yàn)數(shù)據(jù)，雖然翼型噪聲理論預(yù)測(cè)結(jié)果普遍偏大，但是總的趨勢(shì)是一致的.其主要原因是該理論是基于NACA0012翼型的一種半經(jīng)驗(yàn)計(jì)算模型，在某些參數(shù)的確定方面難免有些偏差.

為了研究風(fēng)速對(duì)翼型噪聲特性的影響，分別對(duì)比分析風(fēng)速在45 m/s和60 m/s時(shí) CQU－DTUB18 翼型與 NACA－64－618 翼型的噪聲特性.圖5(c)和圖5(d)分別表示風(fēng)速為45 m/s，CL=0.50 和 CL=0.94 時(shí) CQU－DTU－B18 翼 型 與NACA－64－618翼型的聲壓級(jí)對(duì)比圖.由圖可知:相比 NACA－64－618 翼型，CQU－DTU－B18 翼型能夠產(chǎn)生更低的噪聲值;而且，相比風(fēng)速為30 m/s時(shí)，當(dāng)頻率大于600 Hz時(shí)理論預(yù)測(cè)結(jié)果與實(shí)驗(yàn)值更加接近;當(dāng)風(fēng)速增加到60 m/s時(shí)，翼型噪聲隨頻率變化特性與風(fēng)速為45 m/s時(shí)頗為相似，如圖5(e)和圖5(f)所示.

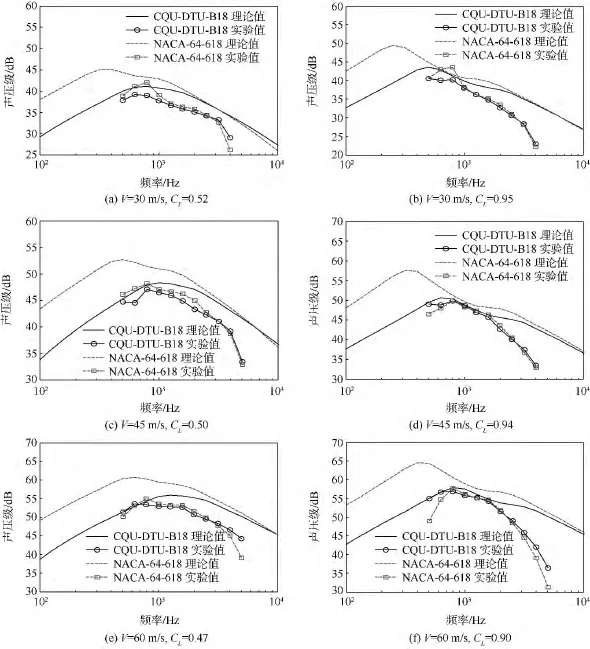
圖5 CQU－DTU－B18 與 NACA－64－618 翼型聲壓級(jí)對(duì)比圖Fig.5 Comparison of sound pressure level for CQU－DTU－B18 and NACA－64－618 airfoil

這兩種翼型總的噪聲大小對(duì)比如表1所示(風(fēng)速為45 m/s).由表可知，在升力系數(shù)為0.50時(shí)，CQU－DTU－B18 翼型能夠產(chǎn)生比 NACA－64－618翼型低約2 dB的噪聲;在升力系數(shù)為0.94時(shí)，CQU－DTU－B18 翼型能夠產(chǎn)生比 NACA－64－618 翼型低約4 dB的噪聲.

表1 光滑條件下風(fēng)速為45m/s時(shí)2種翼型的噪聲值對(duì)比Table1 Comparison of sound pressure level for the two airfoils in clean condition at a wind speed of 45 m/s dB

經(jīng)過(guò)以上噪聲聲壓級(jí)及噪聲大小對(duì)比分析，可以得出:噪聲計(jì)算模型與實(shí)驗(yàn)數(shù)據(jù)吻合得較好;相比 NACA－64－618 翼型，CQU－DTU－B18 翼型能夠產(chǎn)生更低的噪聲，從而研究了該翼型具有良好的低噪聲性能.

5 結(jié)論

1)基于翼型泛函集成理論及翼型噪聲計(jì)算模型，建立了低噪聲翼型優(yōu)化設(shè)計(jì)數(shù)學(xué)模型，提出以翼型最大升阻比與噪聲比值為目標(biāo)函數(shù)，采用RFOIL耦合BPM噪聲計(jì)算模型預(yù)測(cè)翼型噪聲值.優(yōu)化設(shè)計(jì)得到一種低噪聲的新翼型.該方法較好地解決了翼型氣動(dòng)性能與噪聲之間的矛盾，為設(shè)計(jì)低噪聲風(fēng)力機(jī)翼型拓寬了思路.

2)為了驗(yàn)證該翼型具有較低的噪聲特性，對(duì)CQU－DTU－B18 翼型及 NACA－64－618 翼型在相同的噪聲風(fēng)洞實(shí)驗(yàn)中進(jìn)行了噪聲測(cè)試.實(shí)驗(yàn)結(jié)果表明:相比 NACA－64－618 翼型，在相同的升力系數(shù)及風(fēng)速條件下，CQU－DTU－B18翼型具有更低的噪聲大小;雖然基于BPM噪聲計(jì)算模型預(yù)測(cè)結(jié)果與實(shí)驗(yàn)數(shù)據(jù)有一定的偏差，但是升壓級(jí)隨頻率的變化趨勢(shì)是一致的，從而驗(yàn)證了該設(shè)計(jì)方法的可行性，同時(shí)對(duì)于翼型噪聲預(yù)測(cè)具有很好的指導(dǎo)作用.

References)

［1］ 賀德馨.風(fēng)工程與工業(yè)空氣動(dòng)力學(xué)［M］.北京:國(guó)防工業(yè)出版社，2006:221－225.He D X.Wind engineering and industrial aerodynamics［M］.Beijing:National Defense Industry Press，2006(in Chinese).

［2］ Brooks T F，Pope D S，Marcolini M A.Airfoil self－noise and prediction［M］.Washington:NASA，1989.

［3］ Zhu W J，Nicolai H，Shen W Z，et al.Modeling of aerodynamically generated noise from wind turbines［J］.Journal of Solar Energy Engineering，2005，127(4):517－528.

［4］ 司海青，王同光.風(fēng)力機(jī)噪聲的預(yù)測(cè)方法研究［J］.空氣動(dòng)力學(xué)學(xué)報(bào)，2011，29(6):801－804.Si H Q，Wang T G.Predicting method of aerodynamic noise from wind turbine［J］.Acta Aerodynamic Sinica，2011，29(6):801－804(in Chinese).

［5］ 余雷，宋文萍.風(fēng)力機(jī)翼型氣動(dòng)噪聲非線性聲學(xué)計(jì)算［J］.空氣動(dòng)力學(xué)學(xué)報(bào)，2013，31(2):266－272.Yu L，Song W P.Aerodynamic noise prediction for wind turbine airfoils using non－linear acoustics solvers［J］.Acta Aerodynamic Sinica，2013，31(2):266－272(in Chinese).

［6］ Singh R K，Ahmed M R，Zullah M A，et al.Design of a low Reynolds number airfoil for small horizontal axis wind turbines［J］.Renewable Energy，2012，42:66－76.

［7］ Timmer W A，Van Tooij R P J O M.Summary of the Delft University wind turbine dedicated airfoils［J］.Journal of Solar Energy Engineering，2003，125(4):488－496.

［8］ Henriques J C C，Marques da Silva F，Estanqueiro A I，et al.Design of a new urban wind turbine airfoil using a preesure－load inverse method［J］.Renewable Energy，2009，34:2728－2734.

［9］ Ribeiro A F P，Awruch A M，Gomes H M.An airfoil optimization technique for wind turbines［J］.Applied Mathematical Modelling，2012，36(10):4898－4907.

［10］ 劉雄，羅文博，陳嚴(yán)，等.風(fēng)力機(jī)翼型氣動(dòng)噪聲優(yōu)化設(shè)計(jì)研究［J］.機(jī)械工程學(xué)報(bào)，2011，47(14):134－139.Liu X，Luo W B，Chen Y，et al.Research on the aerodynamic noise optimization of wind turbine airfoil［J］.Journal of Mechanical Engineering，2011，47(14):134－139(in Chinese).

［11］ 周大高，柳陽(yáng)威，文曉慶，等.改進(jìn)SA模型對(duì)翼型分離流動(dòng)的數(shù)值模擬［J］.北京航空航天大學(xué)學(xué)報(bào)，2012，38(10):1384－1388.Zhou D G，Liu Y W，Wen X Q，et al.Modification of SA model for predicting airfoil flow separation［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(10):1384－1388(in Chinese).

［12］ 黎作武，陳江，陳寶，等.風(fēng)力機(jī)組葉片的先進(jìn)翼型族設(shè)計(jì)［J］.空氣動(dòng)力學(xué)學(xué)報(bào)，2012，30(10):130－136.Li Z W，Chen J，Chen B，et al.Design of advanced airfoil families for wind turbines［J］.Acta Aerodynamic Sinica，2012，30(1):130－136(in Chinese).

［13］ 王旭東，陳進(jìn)，張石強(qiáng).風(fēng)力機(jī)葉片翼型型線集成設(shè)計(jì)理論研究［J］.中國(guó)機(jī)械工程，2009，20(2):211－213.Wang X D，Chen J，Zhang S Q.Integration study on airfoil profile for wind turbines［J］.China Mechanical Engineering，2009，20(2):211－213(in Chinese).

［14］ Zhu W J，S?rensen J N，Shen W Z.An aerodynamic noise propagation model for wind turbinesH［J］.Wind Engineering，2005，29(2):129－143.

［15］ Brooks T F，Marcolini M A.Scaling of airfoil self－noise using measured flow parameters［J］.AIAA Journal，1985，23(2):207－213.