基于經驗小波變換的目標加速度估計算法

陳浩，郭軍海，齊巍

(北京跟蹤與通信技術研究所，北京100094)

脈沖雷達測速通常采用細譜線跟蹤技術，導彈等高動態目標的加速度和加加速度會使回波多普勒譜線展寬甚至出現混疊，導致雷達測速系統很難正確跟蹤.因此為了提高脈沖雷達多普勒測速精度，估計目標的加速度和加加速度并進行相位補償至關重要［1－2］.當目標作加速運動時，回波信號為相位具有高階項的非平穩信號.目標加速度和加加速度分別對應于回波信號的二階相位系數和三階相位系數.常用非平穩信號參數估計的方法有時頻分析和基于 Hilbert－Huang變換(HHT)［3］參數估計方法.

Wigner－Hough［4］變換、Radon－Wigner［5］變換、Radon－Ambiguity 變換［6－7］、分級傅里葉變換［8－9］等時頻分析方法需要進行一維搜索或二維搜索，計算量較大.經驗模式分解(EMD)［10－11］是一種適用于非平穩信號處理的新方法.信號通過EMD可分解為不同的本征模態函數(IMF).IMF是Huang［10］提出的一種調幅調頻(AM－FM)信號，其目的是為了對IMF作Hilbert變換得到有意義的瞬時頻率(IF).對分解得到的各級IMF作Hilbert變換即可得到對應的瞬時頻率，再利用直接型主成分提取方法(DPCE)［12］或能量型主成分提取方法(EPCE)［13］就能從得到的各組瞬時頻率中得到調頻信號的頻率主成分.在EMD的基礎上，Wu等人提出了一種叫作總體經驗模式分解(EEMD)［14］的噪聲輔助數據分析方法.EEMD能解決EMD的模態混疊(mode mixing)問題，同時對分解的IMF求總體平均，使分解更具有魯棒性，但由于要進行多次EMD分解，也會有計算量大的問題.結合EMD的自適應性和小波分析的理論框架，Gilles提出了一種稱為經驗小波變換(EWT)［15］的自適應信號處理方法.其核心思想是通過對信號的Fourier譜進行自適應劃分，建立合適的小波濾波器組來提取信號不同的AM－FM成分.對不同的信號成分作Hilbert變化可以得到有意義的瞬時頻率，利用類似于EMD的EPCE方法就能提取到調頻信號的瞬時頻率.EWT方法是在小波框架下建立的方法，所以其計算量遠小于EMD方法，而且具有較強的魯棒性.

1 經驗小波變換

經驗小波本質上是根據信號頻譜特性選擇的一組帶通濾波器.為了確定帶通濾波器的頻率范圍，對信號的Fourier譜進行分割.假設將Fourier支撐［0，π］分割成 N 個連續的部分 Λn=［wn－1，wn］，n=1，2，…，N(w0=0，wN= π)，wn選擇為信號Fourier譜相鄰兩個極大值點之間的中點，那么，如圖1所示.圖中的過渡區域以wn為中心，寬度為2τn.確定分割區間Λn后，根據Meyer小波確定的經驗尺度函數和小波函數分別如式(1)和式(2)所示.

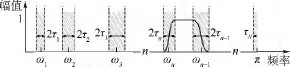
圖1 Foureier坐標系的分割Fig.1 Partitioning of the Fourier axis

式中，τn= γwn;γ ＜ minn［(ωn－1－ ωn)∕(ωn+1+ωn)］;β(x)=x4(35－84x+70x2－20x3).

原始信號可被重構為

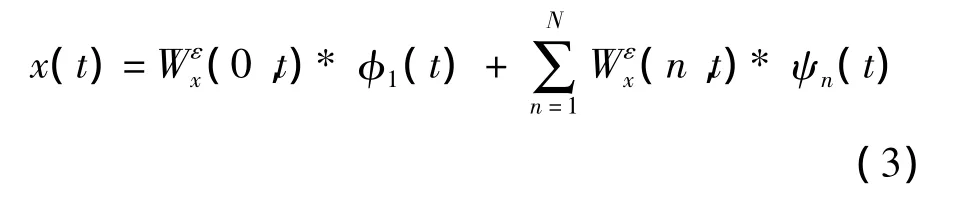
式中:* 為卷積符號;Wεx(0，t)為逼近系數;Wεx(n，t)為x(t)的經驗小波變換，經驗模式xk(t)可定義為

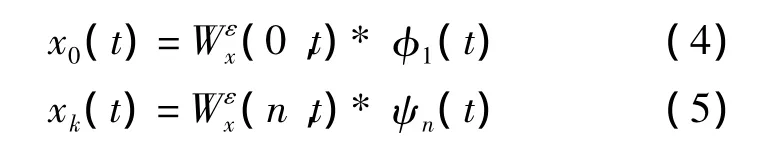
2 基于EWT速度與加速度估計方法

2.1 問題分析

設脈沖雷達發射的單載頻脈沖串信號為

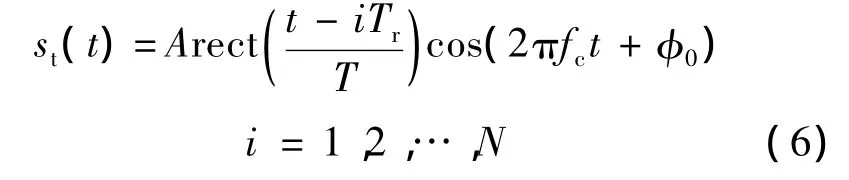
式中，Tr為脈沖持續時間;fc為載波頻率;φ0為初始相位.對應的回波信號為

式中，φd=2π∫fd(t)dt;fd(t)=2v(t)/λ為多普勒頻率，λ為信號波長.通過正交解調得到的輸出信號為

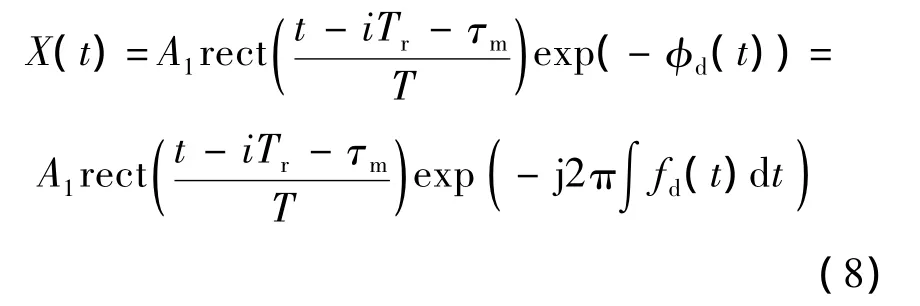
假設積累N個脈沖，每個脈沖采樣一個點來求多普勒速度:

若在t1～tN內目標作加速運動，速度近似為v(t)≈v0+at+ja/2t2，則

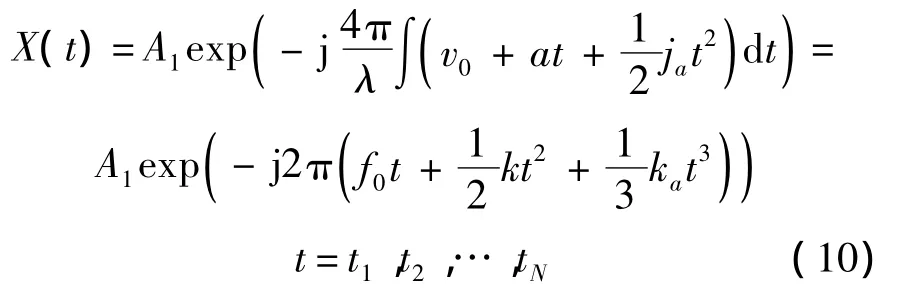
式中，f0=2v0/λ;k=2a/λ;ka=ja/λ，a 為加速度，ja為加加速度，此時回波的相位具有三階相位系數.

2.2 頻率主成分提取

令含噪回波信號的模型為

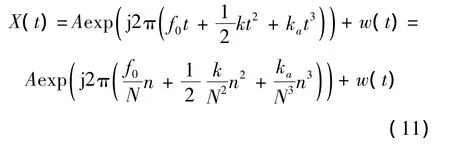
式中，A為幅度;f0為初始頻率;k為二次相位系數;ka為三次相位稀疏;w(t)為引入FM信號中的高斯白噪聲.文中仿真信號設置A=1，f0=100 Hz，k=400，ka=300，采樣率 fs=2500 Hz.

對X(t)作EWT變換得到不同的經驗模式Xk(t)，即 X(t)=Xk(t).對 Xk(t)作 Hilbert變換，可得

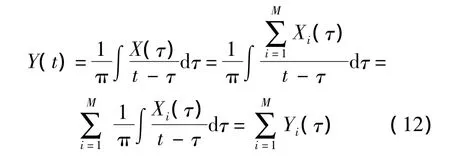
各經驗模式的解析函數為

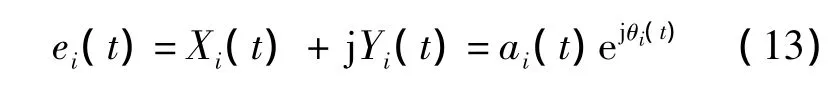
式中，ai(t)為瞬時幅度;θi(t)為瞬時相位;且

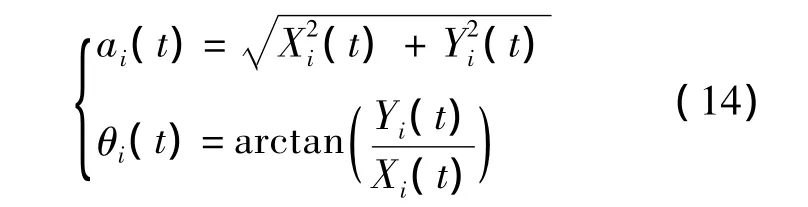
則原信號可表示為

式中fj(t)為第j個經驗模式的瞬時頻率.得到M組瞬時頻率fj(t)后，可利用基于能量型主成分提取方法來提取信號的頻率主成分.對于同一時刻τ，選出各IMF在時刻τ對應的瞬時幅度最大值ak對應的經驗模式的瞬時頻率作為頻率主成分，即

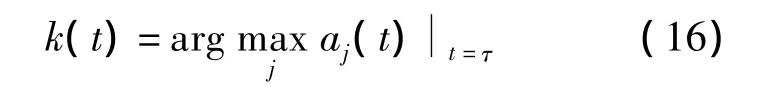
則信號的瞬時頻率為f(t)=fk(t)(t).

2.3 基于EWT的參數估計性能分析

在利用EWT變換進行FM信號參數估計時，實際得到的是一組信號的瞬時頻率點f(t):

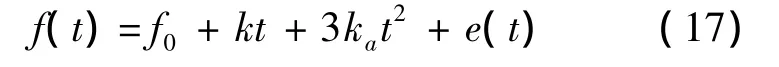
式中e(t)為頻率噪聲.EWT變換等價于一組帶通濾波器，EWT變換得到的不同IMF的瞬時頻率分屬不同的頻率區間.通過頻率主成分提取方法可將不同頻率區間內的瞬時頻率點提取出來，頻率噪聲僅與信號的信噪比相關.利用最小二乘方法可以對參數α=(f0，k，ka)進行估計，因此參數的估計精度僅與回波信號的信噪比相關.由最小二乘估計的性質可知，估計量α^為參數α的線性無偏估計.根據式(13)確定待估參數的 C－R下界［16］為

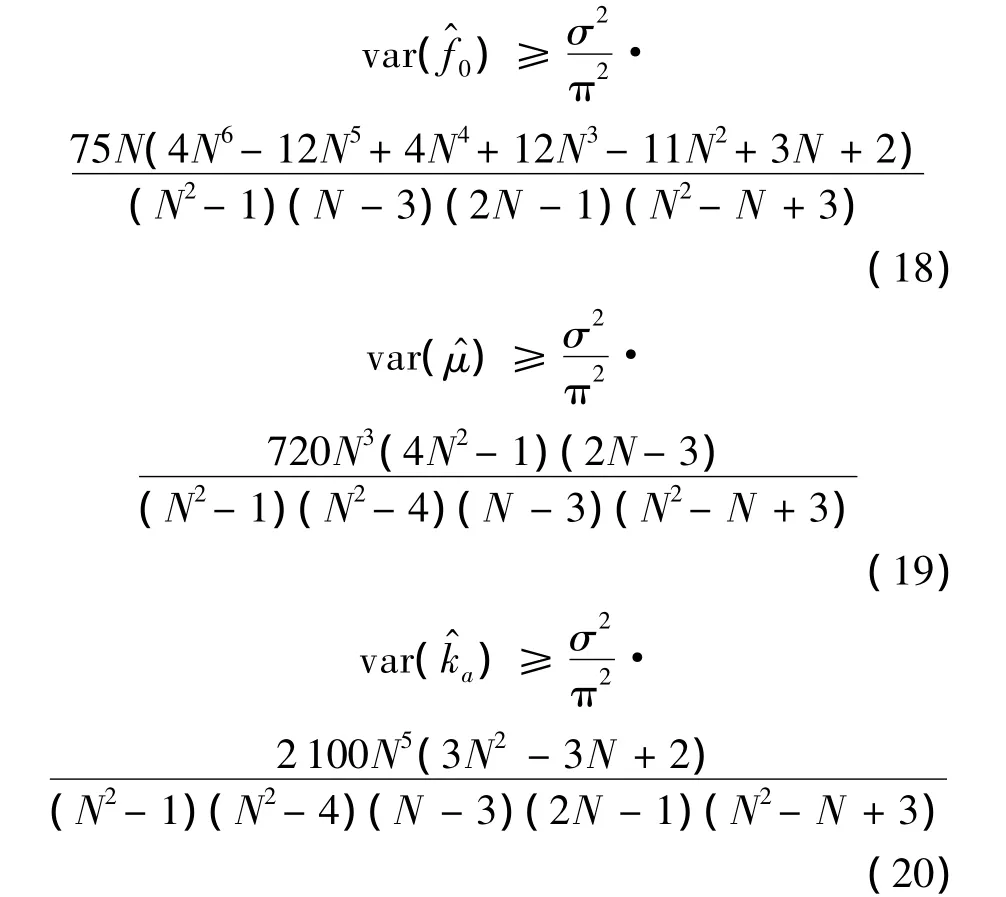
EWT方法是一種小波分析算法，利用Mallat算法［17］可實現快速計算.而傳統的FRFT方法是二維搜索算法，其計算量遠大于EWT算法，導致數據處理速度較慢.因此，EWT算法比FRFT算法更適用于實時數據處理.

3 仿真與分析

3.1 理論數據仿真

理論仿真分為2部分.第1部分僅考慮信號具有二次相位項.

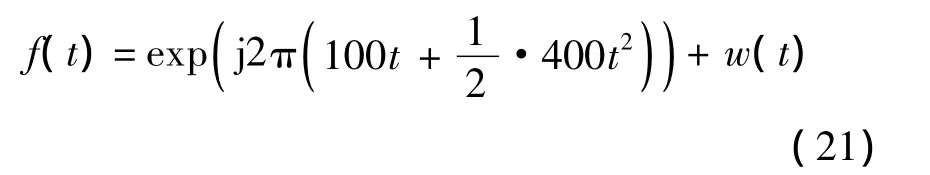
式中w(t)為加性高斯白噪聲.

圖2(a)為信號經EWT變換后得到的各個經驗模式，圖2(b)為信噪比等于10 dB時用EWT方法提取的頻率主成分.從圖2(b)可以看出利用EWT方法提取的頻率主成分受噪聲干擾較小，絕大部分瞬時頻率點都分布在瞬時頻率直線兩端.圖3、圖4分別為5dB＜信噪比＜15dB時，分別用EWT，EEMD－PCA和分數階傅里葉變換(FRFT)方法Monte Carlo仿真50次得到的一次、二次相位系數估計均方根誤差(RMSE)圖，并將各參數估計誤差與C－R下界作比較.從圖3、圖4中可以看出，基于EWT的參數估計方法估計精度要遠遠高于傳統的FRFT方法和EEMD－PCA方法.傳統的FRFT方法在估計線性調頻(LFM)信號初始頻率和高階相位系數時，其估計精度主要受采樣點數N和旋轉角度搜索間隔決定，受信噪比影響不大，因此圖中FRFT方法估計的參數誤差隨信噪比變化不大.EWT方法估計的參數誤差最為接近C－R下界，且隨著信噪比的增大，EWT逐漸逼近于C－R下界.同等硬件條件下EWT方法運行一次的計算時長為0.0079 s，FRFT方法的計算時長為2.711 s，EEMD方法的計算時長為6.328 s.EWT算法由于采用了Mallat小波快速算法，計算速度要遠遠快于FRFT方法和EEMD方法.

圖2 利用經驗小波變換(EWT)算法得到的經驗模式和瞬時頻率Fig.2 Estimated intrinsic mode functions(IMF)and instantaneous frequency(IF)using empirical wavelet transform(EWT)method

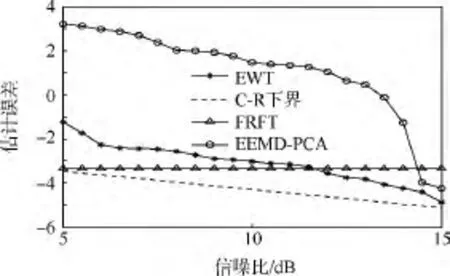
圖3 一次相位系數f0估計誤差Fig.3 Estimating error of coefficient f0

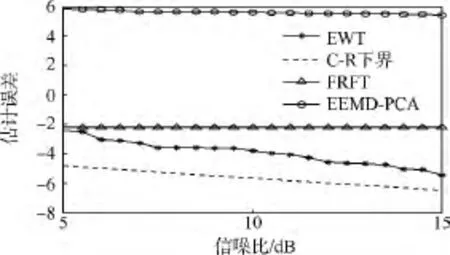
圖4 二次相位系數k估計誤差Fig.4 Estimating error of coefficient k

考慮三階相位項時，假設ka=300，則

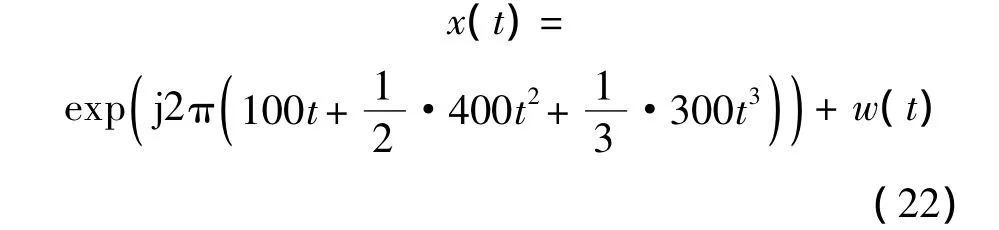
用本文的方法提取得到的瞬時頻率如圖5所示，對獲取的頻率點用抗差最小二乘擬合可估計各階相位系數.對具有三階相位項非平穩信號，傳統的FRFT方法不再適用.因此，將基于EWT方法的參數估計的估計誤差與EEMD－PCA方法和各待估參數的C－R下界作比較.一二階相位系數估計誤差與3.1節類似，三次相位項的估計誤差如圖6所示.信號的瞬時頻率為二次曲線，從圖5可以看出，提取的瞬時頻率集中點分布在二次曲線兩側.從圖6中可以看出，利用本文提出的方法估計得到的信號的三次相位系數估計精度最接近C－R下界，且隨著信噪比的提高，逐漸逼近于C－R下界.

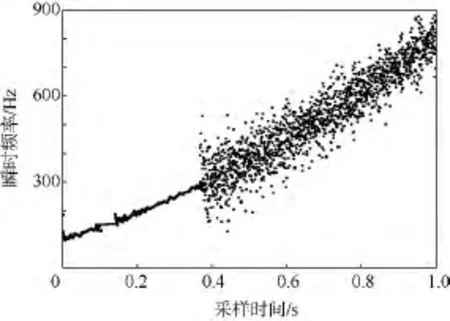
圖5 具有三階相位系數信號的瞬時頻率Fig.5 Estimated instantaneous frequency(IF)of signal with the third order phase coefficients

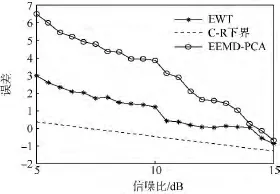
圖6 三階相位系數估計誤差Fig.6 Estimating error of the third order phase coefficient

3.2 實測數據仿真

利用某C波段窄帶脈沖雷達測量得到的飛行器主動段數據進行仿真.為了滿足目標作加速運動或加加速度運動的假設，僅積累50個回波的I/Q數據作為滑動窗口，每個回波采一個點，窗口每次滑動一個點.利用本文的加速度估計算法得到的加速度作相位補償估計的速度誤差如圖7所示.利用真實速度作21點中心平滑得到的加速度均方根誤差為0.03 m/s2，將本文得到的加速度與速度中心平滑得到加速度誤差如圖8所示.從圖中可以看出，利用本文的方法估計的加速度進行相位補償效果很好，使估計的速度誤差小于0.05 m/s，最大加速度誤差小于0.4 m/s2.

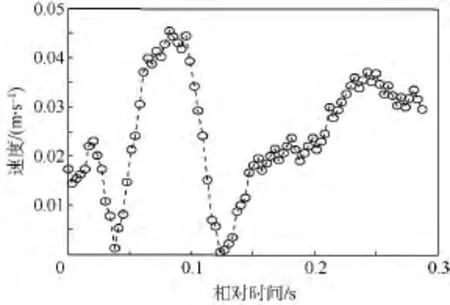
圖7 加速度補償后的速度誤差Fig.7 Velocity error after acceleration compensation

圖8 實測數據加速度誤差Fig.8 Estimated acceleration error of measured data

4 結論

本文在經驗小波變換的基礎上，提出EWT方法對目標徑向加速度進行估計，仿真和理論數據對該算法進行驗證表明:

1)仿真表明該算法在不同的信噪比條件下均能以較高的精度估計信號的參數，估計精度高于傳統FRFT算法和EEMD算法，且估計誤差逼近于C－R下界;

2)計算速度要遠遠快于傳統算法;

3)脈沖雷達實測I/Q數據表明，該算法估計的加速度誤差小于0.4 m/s2，加速度的補償后估計的速度誤差小于0.05 m/s.

References)

［1］ 袁斌，陳曾平，徐世友，等.基于距離單元篩選快速最小熵的含旋轉部件目標相位補償方法［J］.電子與信息學報，2013，35(5):1128－1134.Yuan B，Chen Z P，Xu S Y，et al.Phase compensation for targets with rotating parts based on range bins selection in fast minimum entropy［J］.Journal of Electronics ＆ Information Technology，2013，35(5):1128－1134(in Chinese).

［2］ 夏猛，楊小牛.基于三次相位補償的運動目標參數估計［J］.電子科技大學學報，2013，42(4):559－564.Xia M，Yang X N.Parameter estimation for moving target based on three－phase compensation［J］.Journal of University of Electronic Science and Technology of China，2013，42(4):559－564(in Chinese).

［3］ Cao S，Bing P，Lu J，et al.Seismic data time－frequency analysis by the improved Hilbert－Huang transform［J］.Oil Geophysical Prospecting，2013，48(2):246－254.

［4］ Wang Z Z，Liu F，Huang Y，et al.Digitized periodic wignerhough transform and its performance analysis［J］.Telecommunications Engineering，2012，52(9):1452－1458.

［5］ 歐國建，陳玲瓏，何俞璟.一種多分量LFM信號參數估計的快速仿真算法［J］.重慶郵電大學學報:自然科學版，2013，25(4):459－463.Ou G J，Chen L L，He Y J.A simulation fast algorithm for parameters estimationof the multicomponent LFM signals［J］.Journal of Chongqing University of Posts and Telecommunications，2013，25(4):459－463(in Chinese).

［6］ Yu Y.Detection and parameter estimation of linear frequency modulated signals based on radon transform［J］.Journal of Modern Defence Technology，2013，41(1):136－141.

［7］ Zhu Y W，Zhao Y J，Jia W G.Fast parameter estimation method for LFM signal based on ambiguity function slice and FrFT［J］.Journal of Information Engineering University，2012，13(2):218－223.

［8］ Mohindru P，Khanna R K R，Bhatia S S.Analysis of chirp signal with fractional Fourier transform［J］.Majlesi Journal of Multimedia Processing，2013，2(1):314－322.

［9］ Din? E，Duarte F B，Machado J A T，et al.Application of continuous wavelet transform to the analysis of the modulus of the fractional Fourier transform bands for resolving two component mixture［J］.Signal，Image and Video Processing，2013，21(10):1－7.

［10］ Huang N E.The empirical modedecomposition and the Hilbert spectrum for nonlinear andnon－stationary time series analysis［J］.Proceedings of Royal Society of London，1998，A4(54):903－995.

［11］ Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter bank［J］.Signal Processing Letters，IEEE，2004，11(2):112－114.

［12］ 崔華.一種新的線性調頻信號的瞬時頻率估計方法［J］.計算機應用研究，2008，25(8):2532－2533.Cui H.New method for instantaneous frequency estimations of LFM signals［J］.Application Research of Computers，2008，25(8):2532－2533(in Chinese).

［13］ 王燕，鄒男，付進，等.基于局部瞬時能量密度級的瞬態信號檢測方法［J］.電子與信息學報，2013，35(7):1720－1724.Wang Y，Zou N，Fu J，et al.Transient signal detection method based on partial instantaneous energy density level［J］.Journal of Electronics ＆ Information Technology，2013，35(7):1720－1724(in Chinese).

［14］ Wu Z H，Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method［J］.Advances in Adaptive Data Analysis，2009，1(1):1－41.

［15］ Gilles J.Empirical wavelet transform［J］.IEEE Transactions in Signal Processing，2013，61(16):3999－4010.

［16］ Steven M K.Fundamentals of statistical signal processing，Volume I:estimation theory［M］.Beijing:Publishing House of E－lectronics Industry，2006:25－39.

［17］ 成禮智.小波的理論與應用［M］.北京:科學出版社，2009:75－88.Cheng L Z.Theories and applications of wavelet［M］.Beijing:Science Press，2009:75－88(in Chinese).